有序 有理 有效
——《解决问题的策略(列举)》的教学思考
2016-04-02林锦城
林 萍 林锦城
“解决问题的策略”与传统应用题教学不同,策略是对解决问题方法的理解与升华,树立策略意识、形成基本策略有利于将解决问题的一些具体方法上升为数学思想的感悟。在学生解决问题的过程中,要超越具体的解法,实现数学基本经验的积累与数学思想的感悟,其有效的途径就是组织学生反思、说理,促使学生解题后能沉下心来思考,并外化为数学说理表达,以说理促进内化,在内化、外化的相互作用中实现认知的升华。
下面,笔者就以《解决问题的策略》的课堂教学为例,谈谈如何落实以上的教学思考:
片断一:因需引入,感知策略
师:同学们,林老师在红星小学看到园丁王大叔忙着用木栅栏围花圃,请看!
(出示:王大叔用22根1米长的栅栏围一块长方形花圃)
师:从以上信息中,你能想到什么?
生:花圃是长方形的。
生:长方形的周长是22米。
生:栅栏是1米、1米的,那长方形的长和宽都是整米数。
师:如果你是王大叔,你会怎么围?
生:围一个长10米,宽1米的长方形。
师:他这样围可以吗?为什么可以?
生:10加1等于11,11乘2正好是22米。
师:他运用长方形周长知识验证这种围法是正确的!
师:就只有这种围法吗?(学生许多人举手)看来不止,那你们有没有想过这些围法中哪种围的面积最大呢?
生:不知道。
生:围的方法很多,好像是6乘5。
生:我也觉得可能是长6米宽5米时面积最大,但又不敢肯定。
师:无法确定怎么办?
生:把所有围法都写出来,比一比就知道了。
师:其他同学觉得呢?(许多学生点头)烂笔头胜过好记性!就按这位同学说的办,把你们的思考过程写在纸上,开始吧!
(学生动手尝试,教师巡视,组织汇报)
师:谁愿意将你的想法与大家一起分享?
生:当长方形的长10米,宽1米时,面积是10平方米;当长方形的长8米,宽3米时,面积是24平方米……
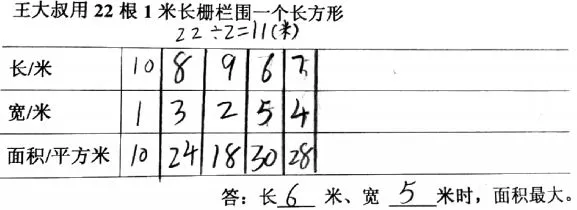
师:除了这5种,还有第6种、第7种吗?
生:没有了,再列举就只能是长5米,宽6米了,但长方形的长应该比宽长,这种不行。
师:对,在二年级时我们就认识过长方形,通常我们都把较长的一条边叫长,较短边叫宽。
师:那怎么围面积最大呢?
生:长6米,宽5米的时候面积最大。
师:其他同学对他这样的列举方法有什么话要说吗?
生:我想提个建议,你这样写太乱了,应该要按顺序。
师:还有不同意见的,那也请你向大家展示下你的想法。

师:大家发现这两位同学的思考方法的最大不同是什么?
生:第二种方法按顺序。
师:有序?从哪里看出的?
生:第二种方法写长的时候按 10、9、8、7、6,从大到小排列,宽从小到大排列。
师:哦,是这样呀!其他同学发现这两种列举方法的不同地方了吗?那你们更欣赏哪一种思考方法?为什么?
生:(齐)第二种好。
师:为什么按顺序思考比较好?第一个同学不按顺序,这5种也都列举出来了呀?
生:按顺序思考不容易漏了。
生:不按照顺序,如果答案不仅仅5种,很多种的时候,写到后面,就可能不知道哪种写过,哪种没写了。
师:刚才同学们把所有围法一种一种写出来,再比一比就知道那种围法面积最大了。想一想,无法确定有几种围法时,更不知道哪种围法面积最大时,你们为什么要把这些围法一一列举出来呢?
生:列举出来就一目了然了。
生:这样就不会重复,也不会遗漏,比一比就知道谁最大了。
师:对了,像刚才这样把所有的可能一一列举出来,就可以找到问题的答案,这是我们解决问题的策略之一。(板书课题)而且呀,大家还讲到,在一一列举时,有序思考(板书:有序)就会不重复、不遗漏(板书:不重复、不遗漏)。
【思考:“策略”教学不同于一般意义的解应用题,需要适时组织学生对解题过程再认识。经历“无法确定哪种围的面积最大,怎么办?”“发现这两种列举方法的不同地方了吗?更欣赏哪一种思考方法?为什么?”“为什么按顺序思考比较好?”“刚才在思考问题时,你们为什么要把这些围法一一列举出来呢?”等多角度的说理活动。一方面学生可以达成解题思路上的共识,加深学生解题方法的内化理解;另一方面也可以使隐含在解题中的“有序列举”策略更加明晰。】
片断二:交流梳理,反思策略
师:分享令我们彼此进步!静下心来回忆一下,刚才我们帮助王大叔解决问题的过程中,采用列举策略,列举时需要注意些什么?
生:列举时要按顺序。
生:不能重复,也不能遗漏了。
师:设想一下,如果这个问题不用一一列举策略能解决吗?
生:不能。
生:可能会,但很难,有时还容易出错。
师:那什么样的问题适合用一一列举解决呢?
生:答案比较多的问题。
生:不能一下子想到所有的答案的时候。
师:在以前的学习中,我们曾经运用列举的策略解决过哪些问题?
生:学习因数和倍数时,用十几个小正方形拼长方形,也是这样一种一种按顺序写出来。
生:还有一年级的时候,10可以分成1和9,2和8……
师:大家记性真好!一一列举可是我们的老朋友了,它的作用很大,平时学习、生活中都经常会不知不觉地用到它。
【思考:学生思维的深度、广度的提升往往有赖于适时、适当的反思。教师提炼“列举时需要注意些什么?”“如果这个问题不用一一列举策略能解决吗?”“那什么样的问题适合用一一列举解决呢?”等问题引发学生的交流,有利于学生对策略意识的内化,而不仅仅埋头于解题活动。】
片断三:尝试应用,完善认知
师:林老师在红星小学还看到学校向同学们推荐了三种杂志,要求学生最少订阅一种,最多订阅三种。
(出示“试一试”:订阅《科学迷》、《文学乐园》、《小灵通》三种杂志,最少订阅一种,最多订阅三种,一共有多少种订阅方法?)
师:如果是你,你会怎么订阅?
生:我会订阅《文学乐园》。
师:他喜欢文学,只订阅一种杂志。
生:我会订阅《文学乐园》和《科学迷》。
师:这位同学兴趣广泛,订阅了两种杂志。
师:仅仅只有这些订阅方法吗?要知道一共有几种订阅方法怎么办?
生:(齐)都写出来。
师:好!在列举时,大家要静下心来想一想,你做到有序了吗?有没有重复的?有没有遗漏的呢?
(学生动手练习,集体汇报。)
师:有同学愿意将他的想法和大家一起分享,让我们一起来听听他的想法!

(学生详细介绍自己的列举方法)
师:这位同学列举方法好吗?好在哪?
生:他列举得很有序,先写完订一种的,再写订阅两种的,最后写订阅三种的。
师:你的评价很到位。是的,他按一定顺序思考问题,而且他思考问题还尤为细致,你看还把它分成了定一种、定两种、定三种的三大类,再一类一类来一一列举。
师:同学们在列举过程中,有没有比他更好的方法?
生:写文字太麻烦,我是用字母表示的。

师:谁看懂他的意思了?他的列举方法又有什么值得我们学习的地方呢?
生:这样写更快了,写文字字太多,太慢。
师:是呀,数学本该如此简洁明了!为了更好地表示想法,我们不但可以用文字表达,也可以用各种符号,像这位同学的字母呀,还有?
生:数字,如 1、2、3。
生:还可以用三角形、正方形、圆分别表示不同的杂志。
……
【思考:解决问题时,策略的采用往往是综合的、交叉的。列举时要做到不重复、不遗漏,有时可以借助分类、画图、列表等方法帮助思考。本环节,组织学生自我推介、赏析他人等方式,要求学生互相评价时不仅仅简单地说“好”或“不好”,贵在要说出其内在的道理:“这样列举有序吗?从哪里看出的?”“他的列举方法又有什么值得我们学习的地方呢?”有理有据的互动活动展示不同解法,既鼓励学生个性化思考,又有利于学生从不同角度领会“列举”的基本方法。】
片断四:实践运用,深化认识
师:下面让我们进入“一锤定音”竞拍时刻!这个汽车模型,它的价格是多少元呢?正确说出它的价格的同学将获得这辆汽车模型的图片一张!
师:第一个提示,本汽车模型的价格,由 1、2、3、4 四个数字组成。那它的价格可能是多少呢?
生:1342。
生:3214。
生:4123。
师:数学呀,可是讲道理的!请想好了再出价!
师:请听第二个提示,在所有可能的价格中,从最低价格数起,排第7位。(学生动手列举)
师:想好了吗?请准备出价!
生:2134。
师:怎么想的?
生:从最低开始 1234、1243、1324、1342、1423、1432,第7个就是2134。
师:他猜对了吗?对,他活学活用今天的知识,有序思考,并做出正确判断,恭喜你!
(许多学生觉得不公平,因为他们也猜出了,但没机会发言)
师:觉得遗憾吧?为了公平,这次报价方式改成竞拍,谁最先想出正确价格,谁将获得第二辆高级跑车!
师:本汽车模型的价格还是由1、2、3、4 四个数字组成。在所有可能的价格中,从最低价格数起,它的价格排第13位。
生:(很快地举手)3124。
师:这么快就知道是3124?怎么想的?
生:因为这里1开头的数有6个,2开头的也有6个,那第13个就是3开头的3124。
(学生鼓掌)
师:大家发现这位同学又快又对获胜的秘诀是什么?
生:他会发现规律。
生:我们都在一个一个地写,他发现了规律就不用一个一个去写了,所以就很快。
生:他会灵活解决问题。
师:说得好!他发现了列举的规律,并灵活解决问题。
师:那如果它的价格排第24位呢?
生:(迫不及待喊出)4321。
师:怎么想的?
生:一共24个,第24位就是最大的那个。
师:真好,玩出智慧了!策略没有最好,关键是具体情况具体分析,并灵活应用!
【思考:解决问题的策略没有最好,贵在何时用,用在什么地方,要避免在教学某一策略时一味强调其优势,而忽视其他方法的使用。本环节在“猜价格”的情境中采用一题多变、一题多问的方式,通过不同层次的设问、访问、追问,组织学生交流解决问题的方法及方法背后所支撑的内在道理——具体问题具体分析,灵活运用。
纵观全课,本课以渗透枚举数学思想方法为主线,通过解决不同的实际问题,引导学生逐步体会一一列举的价值,形成灵活、主动运用策略的意识,并掌握运用这一策略解决问题的基本方法。
