局部支持向量回归在小麦蚜虫预测中的研究与应用

王秀美，牟少敏*，时爱菊，浩庆波.山东农业大学信息科学与工程学院，山东泰安708.山东农业大学化学与材料科学学院，山东泰安708



局部支持向量回归在小麦蚜虫预测中的研究与应用

王秀美1，牟少敏1*，时爱菊2，浩庆波1
1.山东农业大学信息科学与工程学院，山东泰安271018
2.山东农业大学化学与材料科学学院，山东泰安271018

摘要:针对小麦蚜虫预测预警准确率不高的问题，本文提出了一种基于局部支持向量回归的小麦蚜虫短期预测算法。首先用相关分析法进行特征选择，然后进行归一化处理，最后使用局部支持向量回归进行小麦蚜虫百株蚜量短期预测模型的构建，并对未知样本进行预测。利用1990～2013年山东省烟台地区的小麦蚜虫数据及气象数据进行实验，并与标准的支持向量回归进行对比试验。局部支持向量回归的预测以及回代的均方误差为196362和198780，准确率为82.69%和91.03%；支持向量回归的预测以及回代的均方误差为199366和213108，准确率为80.77%和91.03%。实验结果表明，对于小麦蚜虫的短期预测，局部支持向量回归在准确率和推广能力上均明显优于支持向量回归。

关键词:局部支持向量回归；核函数；相关分析；预测；小麦蚜虫

农产品的产量和品质对我国的发展具有举足轻重的作用。小麦是我国主要的粮食作物之一，其年产量居世界第一。而小麦蚜虫则是危害小麦产量和品质的主要虫害[1]。对小麦蚜虫百株蚜量进行准确的预测，可以提早预防，降低其对小麦造成的损失。目前，线性回归[1，2]、马尔科夫链[3]、神经网络[4]等回归分析方法已被应用到虫害发生的预测中，并取得了一定的效果。张永生于2009年将支持向量机用于第2代大豆造桥虫幼虫发生量的预测中，并取得了较为理想的预测结果[5]。2011年，向昌盛等人综合考虑害虫发生量与其影响因子之间的非线性和时滞性关系，借助于支持向量回归（Support Vector Regression，SVR）对山东临沂粘虫幼虫的密度进行预测，实验结果表明，与其它预测方法相比，支持向量机具有较高的预测精度[6]。

近年来，随着对支持向量机研究的深入，Steinwart于2002年证明了在一般情况下，支持向量机并不能满足全局一致性[7]。为进一步改进支持向量机，满足算法的一致性需求。2006年ZHANG等人在局部学习算法的启发下提出了局部支持向量机的思想[8]。局部支持向量机不但具有适合小样本、非线性、高维模式的优势，同时能够满足算法的一致性要求。局部支持向量机被提出后，迅速被应用于金融时间序列预测[9]、短期电力负荷预测[10]等领域。

目前，局部支持向量机应用于虫害发生量预测的研究还尚未见相关文献报道。本文首次将局部支持向量回归应用于小麦蚜虫百株蚜量预测中，构建基于局部支持向量回归的小麦蚜虫短期预测模型，弥补了局部支持向量机在小麦蚜虫预测中的空白。实验结果表明，局部支持向量回归提高了小麦蚜虫预测的准确率，具有一定的研究和应用价值。

1　局部支持向量回归

回归问题的数学描述：对于给定的一组训练样本集（x1，y1），…，（xn，yn），xi∈ Rn，yi∈ R，其中，xi为N维输入向量，称为影响因子，yi为预测对象，寻找与训练样本的输入输出拟合最优的函数关系y＝ f（x），进而对未来样本x的y值进行预测。

1.1支持向量回归

支持向量机解决回归问题的基本思路[11]为：首先通过一个非线性映射φ将样本由输入空间映射到高维特征空间H中；然后在高维特征空间中对样本进行线性回归，找到拟合最优的回归函数f（x）＝w•φ（x）＋b，即最优回归超平面；最后使用最优回归函数对其它样本进行回归预测。标准的支持向量回归的损失函数为ε不敏感损失函数，其数学表达式如公式（1）所示：

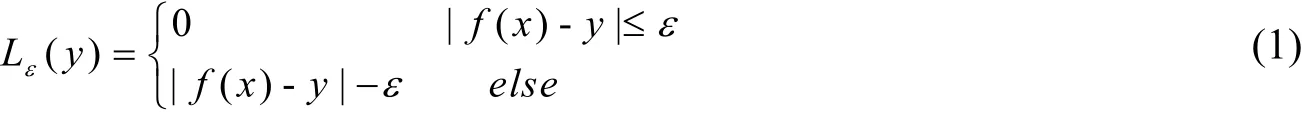
其中，ε为核宽，即回归函数允许的最大误差，使用ε不敏感损失函数可以提高回归模型的泛化能力。

支持向量回归构建回归模型的原则是结构化风险最小化原则，即不仅要使经验风险最小，同时也要降低模型的复杂度，提高模型的泛化能力。支持向量回归求最优回归超平面的问题可以转化为如下的优化问题：

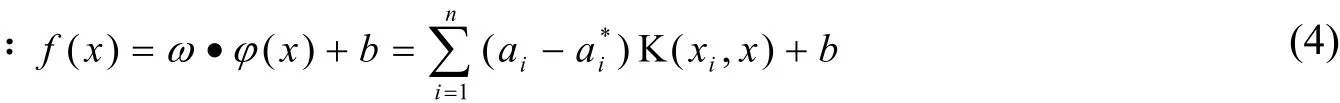
1.2局部支持向量回归

支持向量机使用全部训练样本构造回归模型，忽略了样本的局部变化信息。而局部支持向量机则是在支持向量机的基础上引入了局部学习算法，因此局部支持向量机构造的回归模型蕴含局部化的思想，能够有效地捕捉样本的局部变化趋势，从而提高模型的预测精度[12]。

其中，计算xj*的K近邻时使用的距离函数为欧式距离。

Cheng等人将提出的LSVM用于分类问题，并取得了较好的效果，本文将HLSVM用于回归，得到基于HLSVM的局部支持向量回归（Hard Localized Support Vector Regression，HLSVR），其构造回归模型的步骤如下：（1）确定K值；（2）选取每个测试样本的K个近邻样本；（3）对于选取的K近邻样本，使用支持向量机进行回归建模；（4）使用建立的支持向量回归模型对该测试样本进行预测；（5）对每个测试样本执行（2）～（4），直到所有测试样本预测完成。

与标准的SVR相比，使用HLSVR对测试样本进行预测，可以充分利用样本的局部信息，选取与测试样本相似度较大的样本参与模型的构建，能够有效地提高预测精度；并且HLSVR能够减少参与模型构建的样本数量，从而降低了构建单个模型的时间。

2　基于HLSVR的小麦蚜虫百株蚜量短期预测模型

虫害的发生量是对虫害发生情况预测的主要指标，本文以小麦蚜虫百株蚜量作为预测对象，使用HLSVR构造小麦蚜虫百株蚜量的短期预测模型。由于气象条件对小麦蚜虫的发生有重要影响[2]，因此本模型使用某一时期的百株蚜量（简称虫源基数）和同时期的气象因子作为影响因子，下一时期的小麦蚜虫的百株蚜量作为预测对象，进行回归模型的构建。

基于HLSVR的小麦蚜虫百株蚜量短期预测模型建模过程如下：首先，通过特征选择剔除对预测对象无显著影响的因子；然后，对数据进行归一化处理，提高建模效率；最后，选择合适的核函数及参数构建回归预测模型，并对未来样本进行预测。

2.1特征选择

选择正确有效的特征，对回归模型的构建及预测预报具有重要意义。特征选择作为数据预处理的一个重要过程，其主要任务是去除不相关或者冗余的特征。首先，特征选择可以揭示各个特征对预测对象的重要程度；其次，进行选择特征，可以删掉无关的特征，从而降低数据的维数，缩小问题规模，提高模型的构建效率；最后，特征选择可以使得构建的模型具有更好的泛化能力。

相关分析是研究随机变量之间是否存在某种依存关系的一种常用方法，通过相关分析找到各影响因子与预测对象的相关关系，可以达到特征选择的目的[14]。相关分析得到的相关关系是一种非确定性的关系，它并不能确切到由其中的一个变量去精确决定另一个变量的程度。Pearson相关系数和Spearman相关系数是相关分析中常用的两种相关系数。其中，Pearson相关系数研究的是连续数据之间的相关关系，适用于两个变量之间的相关关系的计算；Spearman相关系数是一种秩相关系数，通过将两列数变为相应的等级，根据等级之差来计算相关系数。

本文构建小麦蚜虫短期预测模型，其影响因子包含多个气象因子，考虑到各气象因子之间存在一定的相关关系，因此通过相关分析删除无关的或者冗余的影响因子，提高构建预测模型的准确率和泛化能力。本文特征选择主要研究的是各个影响因子与预测对象的相关关系，属于变量之间的相关关系，因此采用Pearson相关系数计算相关关系。影响因子Xi与预测对象Y的Pearson相关系数rXi Y的计算公式如下:

其中SXi X i，SYY，SXi Y为Xi，Y的样本方差和协方差。

2.2数据预处理

归一化方法是一种常用的数据预处理方法。归一化方法主要有两种，一种是为了数据处理的方便，将数据映射为0、1之间的小数，另一种是去掉量纲，将有量纲的表达式，化为无量纲的表达式，成为纯量。本文主要考虑不同影响因子的取值范围差距较大，为了避免“大数吃小数”的情况，选用第二种归一化的方法，对各个影响因子进行无量纲化处理，去掉其量纲，公式如下：

针对本文的小麦蚜虫数据，通过多次对比实验发现，仅对影响因子进行归一化比对影响因子及预测对象均归一化的效果明显好，因此，本文将小麦蚜虫的各个影响因子归一化到[0，1]范围内，预测对象未进行归一化处理。

3　小麦蚜虫百株蚜量预测实验及分析

3.1数据来源

本文实验采用的数据主要包含两部分：1990～2013年山东烟台地区小麦蚜虫百株蚜量数据和烟台地区气象数据。我们将1990～2007年（1992～1994年无）的数据作为训练集，2008～2013年的数据作为测试集。预测对象为小麦蚜虫的百株蚜量以及发生程度，其中发生程度据分为5级，轻发生（1级）、偏轻发生（2级）、中发生（3级）、偏重发生（4级）、大发生（5级），主要以小麦蚜虫发生盛期的百株蚜量来确定，各级指标见表1。影响因子为虫源基数（x19）以及降雨量、气温、日照时数等气象因子（x1-x18）。将百株蚜量与19个影响因子进行相关分析，相关系数以及显著性检验结果见表2，其中r为相关系数，P为显著性检验的P值。

表1　小麦蚜虫发生程度分级指标Table 1 The classification index of wheat aphid occurrence degree

表2　相关分析结果Table 2 The result of correlation analysis

取显著性水平为0.5，由表2相关分析的显著性检验结果可知，变量x1～x4、x6、x9、x18的P值均明显大于0.5，与百株蚜量的相关关系不显著，因此，使用其余12个变量预测百株蚜量的值。1990～2007（1992～1994年无）年共78条数据，作为训练样本，2008～2013年共26条数据，作为测试集样本，即本实验样本总数为104。

3.2实验结果及分析

本文利用局部支持向量回归构造小麦蚜虫短期预测模型，并与支持向量回归进行对比实验。核函数是解决非线性回归问题的关键，它可以将样本从低维空间向高维空间进行映射。核函数的类型、核参数的选取直接影响着模型预测精度的高低。目前，RBF核是应用最广泛的核函数。无论样本维数高低、样本数量多少，RBF核函数均可以通过调节其核参数得到较为理想的预测结果[15]。本文两种模型均使用RBF核函数。支持向量回归模型参数的选取采用网格参数寻优，寻优过程采用十折交叉验证法，十折交叉验证可以有效的避免过拟合，是对预测误差的一种比较好的估计[16]。由于局部支持向量回归目前并无较好的调参算法，其惩罚系数C、核宽ε、核参数δ的值与支持向量回归中对应参数的值相等。而对于近邻数K，给定多个值，使用十折交叉验证选择最优的K值。具体选取的参数值见表3。

表3　模型参数Table 3 Model parameter

使用上述两个模型对2008～2013年小麦蚜虫百株蚜量进行预测，百株蚜量的均方误差（Mean Square Error，MSE）以及发生程度的准确率如表4所示所示。MSE表达式为：

其中yi，y’i分别为实际值、预测值，n为测试样本的数目。MSE越小，预测模型的准确度越高。

支持向量回归只需要针对所有训练样本构建一个回归预测模型，对所有测试集样本采用该模型进行预测。而局部支持向量回归则是针对每个测试样本分别建立预测模型，理论上局部支持向量回归比支持向量回归有更好的预测能力以及推广能力。由表4的均方误差可以看出，用HLSVR对1990～2007年的小麦蚜虫数据进行回代检验，其均方误差小于SVR，对于未参与模型构建的2008～2013年的小麦蚜虫的数据，HLSVR模型预测百株蚜量的均方误差明显小于SVR。HLSVR模型以及SVR模型的回代检验的均方误差均高于预测的均方误差，主要是因为1990～2007年小麦蚜虫的百株蚜量存在比较大的值，而2008～2013年小麦蚜虫的百株蚜量值相对比较小，导致回代检验时，较大的百株蚜量对应较大的误差。

表4　均方误差及发生程度准确率Table 4 MSE and the accuracy of classification index

由表4的发生程度的准确率可以看出，对1990～2007年的小麦蚜虫发生程度进行回代检验，HLSVR的回代准确率等于SVR的回代准确率。但是，对2008～2013年的小麦蚜虫的26条数据进行预测，HLSVR的预测准确率明显高于SVR。因此，与SVR相比，基于HLSVR的小麦蚜虫百株蚜量短期预测模型的准确度更高，泛化能力更强。

4　结语

局部支持向量回归既有支持向量回归适合小样本数据、非线性回归问题的优点，同时也可以充分利用样本的局部变化信息，符合算法的一致性要求。本文首次将局部支持向量回归应用于小麦蚜虫短期预测，构建基于HLSVR的小麦蚜虫短期预测模型。使用相关分析法进行特征选择，对影响因子及预测对象进行相关分析，剔除了与预测对象相关关系不显著的因子；使用局部支持向量回归为每个测试样本构建回归模型，提高了模型预测的准确率。实验结果表明，HLSVR比SVR在小麦蚜虫百株蚜量预测中准确率更高，同时HLSVR比SVR的适用性更强。本文的研究成果为虫害短期预测提供了新的思路，具有一定的应用前景。下一步考虑实现基于hadoop的局部支持向量回归，来处理更加复杂的农业数据，进一步提高农业虫害监测预警的准确率。

参考文献

[1]李文峰，尹彬，曹志伟，等.许昌市小麦蚜虫种群变化规律及气象预测模型[J].河南农业科学，2011（3）:81-84

[2]刘明春，蒋菊芳，史志娟，等.小麦蚜虫种群消长气象影响成因及预测[J].中国农业气象，2009（3）:440-444

[3]吴华新，金珠群，韩敏晖.用马尔可夫链分析法预测棉铃虫发生趋势[J].浙江农业学报，2003（6）:33-36

[4]靳然，李生才.基于小波神经网络的麦蚜发生量预测研究[J].天津农业科学，2015（4）:127-131

[5]张永生.支持向量机在害虫预测预报中的应用[J].现代农业科技，2009（14）:147-148

[6]向昌盛，周子英，张林峰.支持向量机在害虫发生量预测中的应用[J].生物信息学，2011（1）:28-31

[7] STEINWART I. Support vector machines are universally consistent [J]. Journal of Complexity，2002，18（3）:768-791

[8] ZHANG H，BERG AC，MAIRE M，et al. SVM KNN: discriminative nearest neighbor classification for visual category recognition[C] //Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York:IEEE，2006:2126-2136

[9] HAIQIN YANG，KAIZHU HUANG，IRWIN KING，et al. Local support vector regression for time series prediction [J]. Neurocomputing，2009，72（10-12）:2659-2669

[10]李以志.基于粒子群优化的局部支持向量回归短期电力负荷预测建模方法研究[D].上海:华东理工大学，2012:26-35

[11]曾绍华.支持向量回归机算法理论研究与应用[D].重庆:重庆大学，2006:9-15

[12]尹传环，牟少敏，田盛丰，等.局部支持向量机的研究进展[J].计算机科学，2012（1）:170-174，189

[14] CHENG H，TAN PN，JIN R. Localized support vector machine and its efficient algorithm[C]//Proc. of STAM International Conference on Data Mining 2007，Minneapolis，Minnesota，2007:461-466

[15]程涛，慕运动，曹建莉.方差分析与相关分析在分层次教学中的应用[J].荆楚理工学院学报，2011（9）:59-62

[16]林升梁，刘志.基于RBF核函数的支持向量机参数选择[J].浙江工业大学学报，2007（2）:163-167

[17]杨柳，王钰.泛化误差的各种交叉验证估计方法综述[J].计算机应用研究，2015（5）:1287-1290，1297

Research and Application of Local Support Vector Regression in Prediction of Wheat Aphid

WANG Xiu-mei1，MU Shao-min1*，SHI Ai-ju2，HAO Qing-bo1
1. College of Information Science and Engineering/Shandong Agricultural University, Taian 271018，China
2. College of Chemistry and Material Science/Shandong Agricultural University, Taian 271018，China

Abstract:Aiming at the accuracy of wheat aphid prediction is low，this paper proposed a short-term forecasting algorithm of wheat aphid based on local support vector regression. Firstly，feature selection was realized by correlation analysis. Secondly，the normalized processing of selected features was calculated. Finally，the short-term forecasting model was established and the prediction value of test sample was obtained by the established model. Experiments were conducted on the wheat aphid data and meteorological data of Yantai area from 1990 to 2013 year and contrast test was conducted by the standard support vector regression. The standard support vector regression achieved the Mean Square Error at 199366 in prediction and 213108 in back-substitution check，the accuracy at 80.77%in prediction and 91.03%in back-substitution check，while local support vector regression achieved the Mean Square Error at 196362 in prediction and 198780 in back-substitution check，the accuracy at 82.69%in prediction and 91.03%in back-substitution check. The results showed that local support vector regression has better performance in accuracy and generalization ability for the short-term prediction of wheat aphid.

Keywords:Local support vector regression；kernel function；correlation analysis；prediction；wheat aphid

*通讯作者：Author for correspondence. E-mail:msm@sdau.edu.cn

作者简介：王秀美（1992-），女，山东潍坊人，硕士研究生，主要研究方向:机器学习. E-mail:wxmsdau@163.com

基金项目：山东省自然基金（ZR2012FM024）

收稿日期：2014-07-12修回日期：2014-09-24

中图法分类号:TP391

文献标识码:A

文章编号:1000-2324（2016）01-0052-05