一道题目的解题视角



○解题研究○

一道题目的解题视角

陈昭亮

(陕西省西安中学,710018)

罗增儒先生在《数学解题学引论》中提出,数学解题是数学学习中不可或缺的核心内容．解题是一种认识活动,是对概念、定理的继续学习,是对方法的继续熟练,而不仅仅是“规则的简单重复”或“操作的生硬执行”.解题的思维活动,正是从已明确地给予的、已知的东西出发,去发现隐蔽存在的、待求解(证)的结论.这是一个积极而生动的发现过程、创造过程.

当解题由一个步骤推进到另一个步骤时,其实就是知识点之间的联系与生成;

当解题由一个关系结构对应到另一个关系结构时(比如由形到数、或由数到形),其实就是关系结构之间的联系与生成;

当解题并列着多个解法时,其实就意味着产生不同解法的知识点之间存在逻辑联系或对应关系.

笔者随着教学实践的深入,对罗先生的这些观点认识愈加深刻,从而也促进笔者更加有意识地进行解题分析,以典型题目的透彻分析促进学生解题能力的有效提升.本文以笔者对一道课本题目的教学及思考为例,说明笔者学习解题分析的过程及教学启示．

一、问题提出

笔者在教学高中数学选修2-2(北师大版)的“综合法与分析法”的习题课时,选用了教材第12页习题1-2的第4题:已知a,b,c,d都是实数,且a2+b2=1,c2+d2=1,求证:

|ac+bd|≤1．

笔者在思考后发现这道题目平中透奇,不但具有很好的数学背景,而且还能变式探究,得出这类问题的一般规律,是提升学生思维品质的好素材．

二、问题解决

思路1数学(选修2-2)教师教学用书上给出的证明方法:利用了已知条件的结构特征进行联想,由a2+b2=1联想到三角函数中的cos2α+sin2α=1.所以,我们设

a=cosα,b=sinα,

c=cosβ,d=sinβ,

则|ac+bd|=cosαcosβ+sinαsinβ|

=|cos(α-β)|

≤1.

思路2由已知条件的a2,b2,c2,d2及结论中的ac+bd等结构特点,联想到构造柯西不等式证明．由柯西不等式知

(ac+bd)2≤(a2+b2)(c2+d2)；

又因为a2+b2=1,c2+d2=1,

从而(ac+bd)2≤1．

所以|ac+bd|≤1．

思路3由a2+b2=1,c2+d2=1,的结构特点,把他们分别看作向量m=(a,b),n=(c,d)模的平方,故可考虑构造向量

m=(a,b),n=(c,d),

所以|m·n|=|m||n||cos〈m,n〉|

=|cos〈m,n〉|；

又|m·n|=|ac+bd|,

所以|ac+bd|=|cos〈m,n〉|

≤1．

思路4由已知中的a2+b2,c2+d2及结论中的ac,bd联想到完全平方公式,故可考虑利用a2+b2≥2ab,c2+d2≥2cd这两个不等式来证明．

因为2=a2+b2+c2+d2

=(a2+c2)+(b2+d2)

≥2|ac|+2|bd|

=2(|ac|+|bd|)

≥2|ac+bd|,

所以|ac+bd|≤1．

思路5考虑到已知条件和要证结论中都有数字1,故可考虑把要证明不等式中的1替换为(a2+b2)(c2+d2),然后再用分析法证明．证明过程简述为:

要证明|ac+bd|≤1,只需证明(ac+bd)2≤1,从而只需证明(ac+bd)2≤(a2+b2)(c2+d2),从而只需证明a2c2+2abcd+b2d2≤a2c2+b2d2+a2d2+b2c2, 即只需证明2abcd≤a2d2+b2c2，即0≤(ad-bc)2,这显然成立，从而原不等式成立．

本题五种解题思路的得出,源自笔者备课时的精心预设(思路1、2、3),以及课堂上的意外生成(思路4、5),正如苏轼在《题西林壁》中的诗句:横看成岭侧成峰,远近高低各不同．事实上,寻找解题思路的过程就是寻找条件与结论之间逻辑联系或转化轨迹的过程,在这个过程中,我们激活知识、检索知识、提取知识、组织知识,使解题与发展同行.所以，罗增儒先生认为:解题活动是掌握数学、学会“数学地思维”的关键途径.

三、结论的应用

在探究了本题的不同解题方法之后,笔者又顺势而下,引导学生进行解题反思,抽丝剥茧,从这一个问题的解答得出一类问题的解答,从而达到对这类问题的本质领悟．

引申1已知a,b,c,d都是实数,且a2+b2=p,c2+d2=q,求|ac+bd|的最大值．

解仿照思路1,利用三角换元法．设

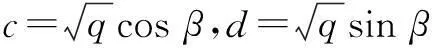
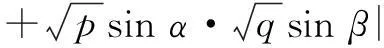
引申2已知a,b,c,d,e,f都是实数,且a2+b2+c2=p,d2+e2+f2=q,求|ad+be+cf|的最大值．

解上面的三角换元法对本题失效,说明三角换元法有局限性,我们应该寻求更一般的解法．这里用柯西不等式解答．

∵(ad+be+cf)2

≤(a2+b2+c2)(d2+e2+f2)

=pq,

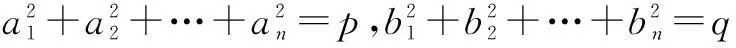
解由柯西不等式，得

(a1b1+a2b2+…+anbn)2

=pq,

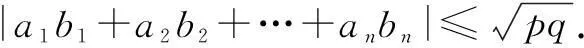
四、教学启示

这种对一道典型题目进行多角度解题分析,能使学生从题目的结构特点上、数字特点上、已知和未知的联系上等多角度看待问题.如，本题中根据a2+b2=1联想到的cos2α+sin2α=1(思路1)、向量m=(a,b)的模(思路3),从已知a2+b2=1,c2+d2=1和未知中的ac,bd及ac+bd的结构联想到柯西不等式(思路2)、基本不等式(思路4).从而揭示出数学内容的更内在的逻辑结构和更直截了当的关系,进而推动解题过程的改进,解题成果的扩大,解题模式的积累,解题经验的生成.进一步从本题出发又拓展出引申1、引申2、引申3,不断抽丝剥茧,抛开了题目对数字的依赖,从特殊走向一般.这道题目的解题过程启发我们在教学中要通过典型题目的多角度、多视角的剖析,引导学生从“数学地思维”到“通过练习学会思维”．