某高校甲型H1N1流感传播元胞自动机模拟研究

关　鹏，毕　雪，费良儒，黄德生，刘　磊

(1 中国医科大学公共卫生学院，辽宁 沈阳　110122；2 中国医科大学公共基础学院，辽宁 沈阳　110122)



·论著·

某高校甲型H1N1流感传播元胞自动机模拟研究

关鹏1，毕雪1，费良儒2，黄德生2，刘磊1

(1 中国医科大学公共卫生学院，辽宁 沈阳110122；2 中国医科大学公共基础学院，辽宁 沈阳110122)

[摘要]目的探索元胞自动机(CA)在模拟分析甲型 H1N1 流感暴发传播中的应用价值。方法通过中国知识基础设施工程(CNKI)查询 2009年1月—2015年3月间公开发表的甲型 H1N1 流感相关文献，按纳入标准选择并提取流感疫情数据，并以重庆市某综合性大学2009 年 10 月 12 日—11月 20 日发生的一起甲型H1N1流感疫情为数据原型，利用 Matlab 7.0 软件构建CA模型，对疫情进行模拟和分析。结果该高校共有在校学生17 820名，2009年流感疫情持续时间为 40 d，当近距离有效感染发病率为0.04 时，CA模型对此次疫情的模拟情况最好，基本再生数为 1.202。结论CA在模拟一定条件下经空气传播性疾病的流行特征方面具有一定的可靠性，可为疾病的预防与控制提供参考依据。

[关键词]甲型H1N1流感； 元胞自动机； 基本再生数； 传染病； 模型

[Chin J Infect Control，2016，15(2)：79-82]

现实世界中与传染性疾病相关的各种类型数据或变量之间通常具有复杂的关系，相互交织形成网络并呈现出复杂的动力特性[1]，因此在对传染病流行规律的理论性研究中，网络动力学模型的研究进展迅速[2-3]。一种空间、时间、状态完全离散的非线性动力系统模型—元胞自动机(cellular automata，简称CA)作为复杂系统和网络研究的有力工具被应用于分析多种传染病问题[4]。本研究基于公开发表的甲型H1N1流感疫情数据，探索CA模型在模拟甲型H1N1流感疫情中的应用情况，试图为疫情的科学评估提供依据。

1资料与方法

1.1资料来源通过中国知识基础设施工程(National Knowledge Infrastructure，CNKI，网址：www.cnki.net)，查询2009年1月—2015年3月间发表的所有甲型H1N1流感相关文献。在期刊文献题目和摘要中进行相关自由词的组合检索。以“甲型H1N1流感、传染病、甲型流感、传染性疾病、流行性感冒和突发公共卫生事件”为主题词或关键词进行检索，同时对文献中的参考文献进行人工检索及筛查。

1.2资料提取标准和质量控制对收集到的所有文献进行筛选，剔除无数据的理论性研究，收录有具体疫情数据的文献，收集疫情数据中疫情的起止时间、每天新发病例数，患者性别、年龄，发生地点(年级、班级、寝室)以及单位的机构类型等。将上述信息核对后建立数据库并存储为.xls格式，供后续CA建模使用。为保证文献摘录质量，上述资料检索和数据提取、录入过程均由两人独立完成，并经核对一致后方进行后续建模。

1.3CA建模

1.3.1CA原理CA为一种在时间、空间和状态上均离散的动力系统，其最基本的组成部分包括元胞(cell)、元胞空间(lattice)、邻居(neighbor)、规则(rule)和时间(time)[5]。

2结果

2.1基本情况该高校位于重庆市大学城中，是一所包含13所院系、506个班级、3 822间寝室的综合性院校，共有在校学生17 820名，其中男性12 710名，女性5 110名。所有在校学生居住的寝室为4～6人间，寝室内环境卫生及通风情况均良好。此次甲型H1N1流感疫情，单日最高病例为74例，最低为8例，每日病例分布见图1。

图1 　2009年重庆某高校甲型H1N1流感病例分布图

2.2基于CA的疫情模拟以该校全体师生为研究对象，总人数为17 820名，因134×134=17 956与该校总人数接近，故取M=N=134的方形区域。此次疫情流行日数约40 d，故取T=40 d；根据甲型H1N1流感本身的流行病学特征，患者出现明显临床症状的平均时间为4 d，所以取Ta(第a天出现临床症状)=4；由于本次患者基本无复发现象，所以取Tb(免疫持续时间)=360；此次甲型H1N1疫情的潜伏期多为1～3 d，少数患者可长达7 d，所以取Tc(潜伏期)=2 d；根据甲型H1N1相关报道可知，该病患者发病后7 d内均具有传染性，由于取Ta=4 d，所以Td(症状不明显但有感染性日数)为3 d；P1为在仿真模拟过程中根据实际结果确定，P2取值为 0.001。

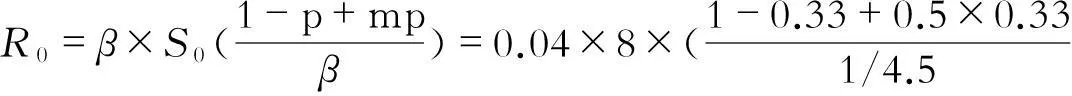
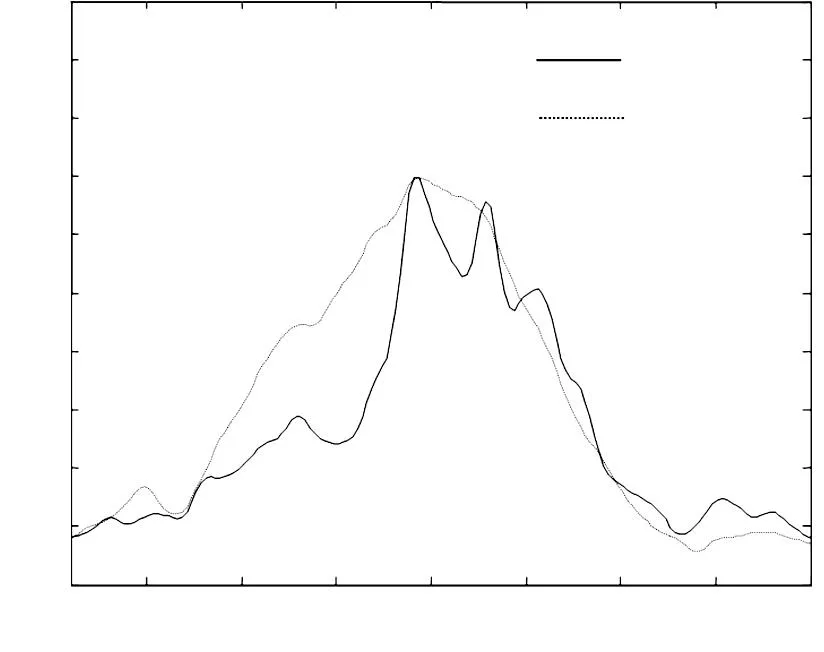
图2 　某高校甲型H1N1疫情的CA模拟图(P1=0.040)

Figure 2Cellular automata graph of epidemic of influenza A(H1N1) in a university (P1=0.040)

图3 　某高校甲型H1N1疫情的CA模拟图(P1=0.045)

Figure 3Cellular automata graph of epidemic of influenza A(H1N1) in a university (P1=0.045)

图4 　某高校甲型H1N1疫情的CA模拟图(P1=0.050)

Figure 4Cellular automata graph of epidemic of influenza A(H1N1) in a university (P1=0.050)

3讨论

本研究将基于CA对流感疫情的仿真结果与实际结果进行了对比，发现两者基本相符，证明了CA在仿真模拟方面的可行性和一定的可靠性。模拟研究可以预测出疫情的高峰日期，若在流行达到高峰日期前即采取合理的防控措施，则有望成功防止疫情扩散，较好的保护易感人群。研究通过R0判断疫情是否得到控制，结果显示为较弱程度的疫情传播，为确定取消隔离等防控措施的时间提供了参考依据。

本研究仅针对发病数据利用CA进行了仿真模拟，结果符合实际流行情况，但并未获得该人群在通过隔离等措施降低人口密度，降低接触率及提高医院诊疗水平等方面的具体信息。此次疫情是重庆市整个大学城疫情的一部分，与周边高校相比，该校疫情程度轻，持续时间短，疫情并未对学校正常的教学秩序产生影响，学校未采取停课等特殊措施[6]。本次模型构建研究中未对人为干预参数加以特殊设置，或者可以认为人为干预由始至终均为恒定值，重点模拟在保持现有措施的情况下疫情的发展趋势。课题组后续将与疾病预防控制部门建立联系，详细收集疾病预防控制部门介入某起传染病疫情并采取防控措施之后的疾病流行情况，如何时采取何种措施、每种措施的实施力度等信息，继续探索CA在实施各种防控措施后对传染病流行情况的模拟和评价[11-13]。

[参 考 文 献]

[1]Nsoesie EO, Brownstein JS, Ramakrishnan N, et al. A systematic review of studies on forecasting the dynamics of influenza outbreaks[J]. Influenza Other Respir Viruses, 2014,8(3):309-316.

[2]Cherif A. Mathematical analysis of a multiple strain, multi-locus-allele system for antigenically variable infectious diseases revisited[J]. Math Biosci, 2015,267:24-40.

[3]Pellis L, Ball F, Bansal S, et al. Eight challenges for network epidemic models[J]. Epidemics, 2015, 10:58-62.

[4]毕雪, 苏弘博, 郭佳慧, 等.元胞自动机及其在传染病防控领域中的应用[J].实用预防医学, 2015, 22(6):766-769.

[5]Wolfram S. Cellular automata as models of complexity[J]. Nature, 1984,311(5985):419-424.

[6]张莉, 郭萍.某高校流感样病例爆发疫情的流行病学调查及应对模式探讨[J].保健医学研究与实践, 2010, 7(2):45-47.

[7]白振国.周期传染病模型的基本再生数[J].工程数学学报, 2013, 30(2):175-183.

[8]陈田木, 刘如春, 谭爱春, 等.隔离患者对控制学校甲型H1N1流感暴发疫情效果的数学模拟[J].中国卫生统计, 2014, 31(3):390-394.

[9]Fraser C, Donnelly CA, Cauchemez S, et al. Pandemic potential of a strain of influenza A (H1N1): early findings[J]. Science, 2009, 324(5934):1557-1561.

[10] Shen M, Xiao Y, Rong L. Modeling the effect of comprehensive interventions on Ebola virus transmission[J]. Sci Rep，2015,5:15818.

[11] López L, Burguerner G, Giovanini L. Addressing population heterogeneity and distribution in epidemics models using a cellular automata approach[J]. BMC Res Notes, 2014,7: 234.

[12] Santos LB, Costa MC, Pinho ST, et al. Periodic forcing in a three-level cellular automata model for a vector-transmitted disease[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2009,80(1 Pt 2):016102.

[13] Sun GQ, Liu QX, Jin Z, et al. Influence of infection rate and migration on extinction of disease in spatial epidemics[J]. J Theor Biol, 2010, 264(1):95-103.

(本文编辑：文细毛)

Simulation of the epidemic of influenza A(H1N1) in a university using cellular automata model

GUANPeng1,BIXue1,FEILiang-ru2,HUANGDe-sheng2,LIULei1

(1SchoolofPublicHealth,ChinaMedicalUniversity,Shenyang110122,China;2SchoolofFundamentalSciences,ChinaMedicalUniversity,Shenyang110122,China)

[Abstract]ObjectiveTo explore the application value of cellular automata(CA) in simulating the epidemic spread of outbreak of influenza A(H1N1).MethodsThe publications regarding influenza A(H1N1) from January 2009 to March 2015 were collected from the China National Knowledge Infrastructure(CNKI), epidemiological data of H1N1 were retrieved according to inclusion criteria, the Matlab 7.0 software was adopted to construct CA model for simulating and analyzing the epidemic of H1N1 occurred in a university in Chongqing between October 12 and November 20,2009.ResultsThere were a total of 17 820 students in this university, the epidemic of influenza lasted 40 days in 2009; When the parameter, the effective infection rate was 0.04, the model of CA fit well, and gave estimate for basic reproduction number (R0) 1.202.ConclusionCA has certain reliability in simulating epidemics of airborne infectious diseases, it can provide reference for the prevention and control of disease.

[Key words]influenza A(H1N1); cellular automata; basic reproduction number; infectious disease; model

[中图分类号]R511.7

[文献标识码]A

[文章编号]1671-9638(2016)02-0079-04

DOI:10.3969/j.issn.1671-9638.2016.02.002

[作者简介]关鹏(1976-)，女(满族)，辽宁省沈阳市人，教授，主要从事传染病流行病学研究。[通信作者]关鹏E-mail:pguan@mail.cmu.edu.cn

[基金项目]国家自然科学基金(71573275; 71073175)

[收稿日期]2015-09-29