考虑转矩波动的电动汽车舒适性稳健性优化*

吴光强　张瑛　郭强

（1.同济大学，上海201804；2.东京大学生产技术研究所，东京153-8505）



考虑转矩波动的电动汽车舒适性稳健性优化*

吴光强1,2张瑛1郭强1

（1.同济大学，上海201804；2.东京大学生产技术研究所，东京153-8505）

【摘要】针对分布式驱动电动汽车存在转矩波动和非簧载质量增加的问题，建立了整车刚柔耦合多体系统模型，同时考虑永磁同步电机磁场的非正弦分布，建立了相应的Matlab/Simulink模型，并利用两者联合仿真模型研究了转矩波动及非簧载质量对电动汽车舒适性的影响规律。基于响应面近似模型，利用多目标优化方法对车辆舒适性进行了稳健性优化。结果表明，优化后不仅提高了车辆的舒适性，同时也提高了车辆的可靠性。

1　前言

分布式驱动电动汽车以布置方便、能量利用率高等特点在电动汽车中占有重要位置。但是分布式驱动电动汽车也存在诸多问题，如轮毂电机导致了转矩波动，同时增加了车辆的非簧载质量，这些因素都会对车辆的动力学性能产生影响。

对此，国内外许多学者进行了大量研究，如有的学者通过在车轮上添加质量块的方法来研究非簧载质量对车辆舒适性的影响[1，2]；有的学者研究了转矩波动对汽车纵向振动的影响，并采用了矢量控制方法来改善振动性能[3]；有的学者通过对悬架衬套和弹簧进行确定性优化来减少转矩波动对车辆舒适性的影响[4]。但这些研究均未考虑不确定性因素的影响，而在实际生产制造中，弹簧、衬套等元件的制造过程必然存在误差，这些误差会对车辆的性能产生较大影响。为此，本文通过建立分布式驱动电动汽车整车刚柔耦合模型和永磁同步电机模型，分析了在转矩波动和非簧载质量共同影响下车辆舒适性的变化规律，并且以转矩波动、元件制造误差等为不确定因素进行了稳健性优化，进而提高了车辆的舒适性。

2　分布式驱动电动汽车模型的建立

2.1刚柔耦合整车模型的建立

车辆系统中包含许多运动部件，尤其在悬架内很多零部件由于采用强度高的材料而刚度很大，常作为刚体进行建模。但随着对模型精度要求的日益增高，仿真时要求某些部件应能够作一定变形，而刚柔耦合建模便是解决此问题的方法[5]。

本文的参考车型为一款集中驱动电动汽车，其前悬架为麦弗逊悬架，后悬架为扭转梁悬架，建模过程中的部件参数均由试验测得。柔性件主要包括前悬架的横向稳定杆（图1）、后悬架的扭转梁及左右两根纵臂。

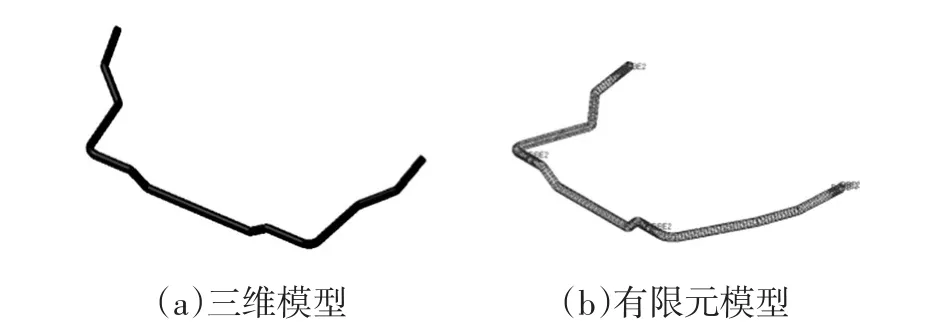
图1　横向稳定杆模型

在此基础上建立了包含前后悬架系统、转向系统、轮胎系统、人体-座椅-车身系统的整车刚柔耦合模型，如图2所示。其后悬架为扭转梁半独立悬架，由横梁、纵臂、弹簧和减振器以及Panhard杆组成。其整车参数如表1所列。

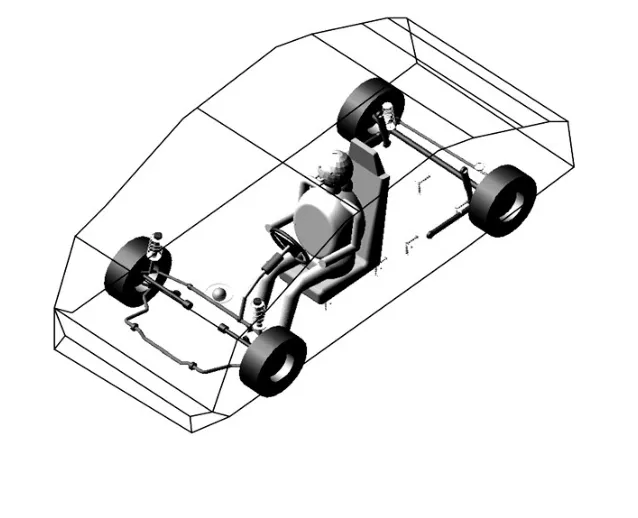
图2　整车刚柔耦合模型

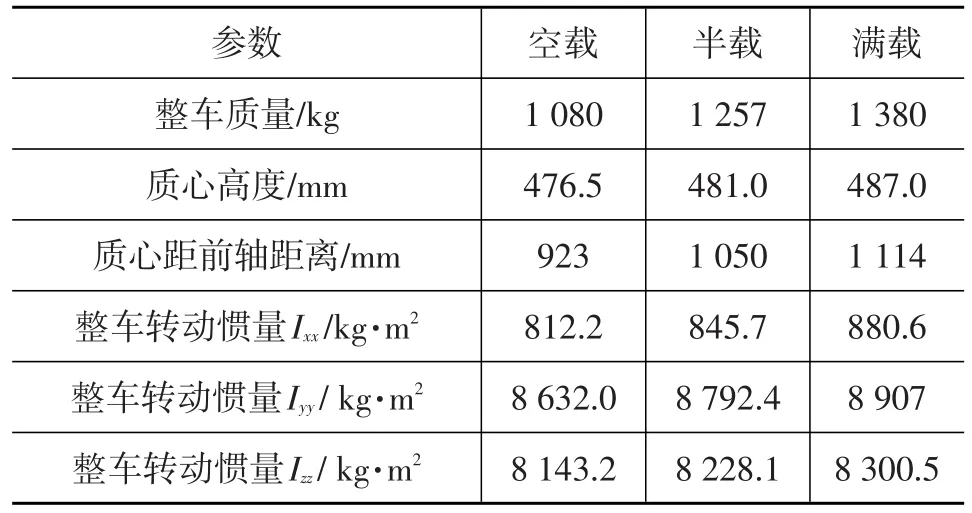
表1　整车参数

2.2永磁电机模型的建立

永磁同步电机[6]的数学模型主要包括电压-磁链方程、转矩方程与运动方程，当电机的磁场非正弦分布时，电机存在6倍基频的转矩波动[7]。

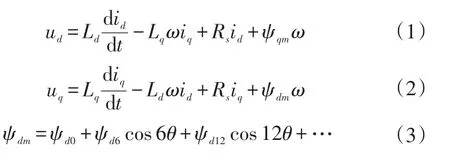
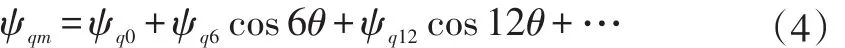
电压-磁链方程为：ψd0、ψd6、ψd12...以及ψq0、ψq6、ψq12…的计算方法为：

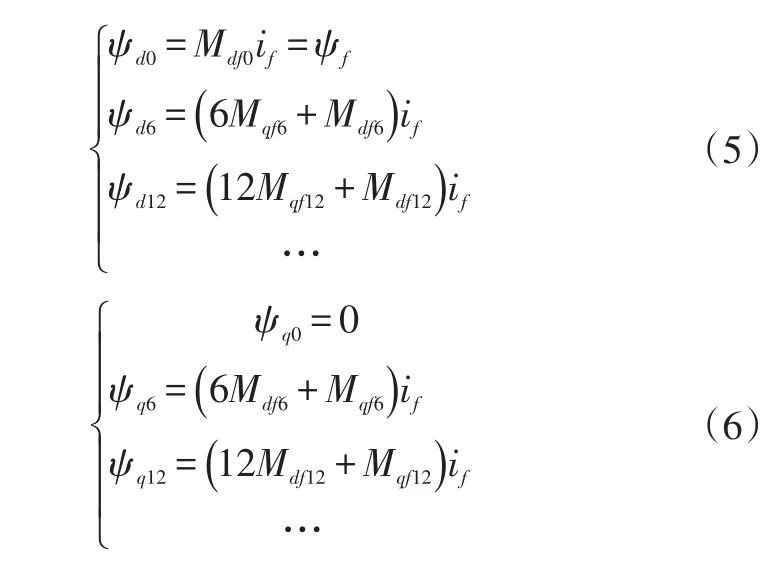
转矩方程为：

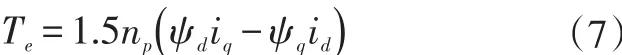
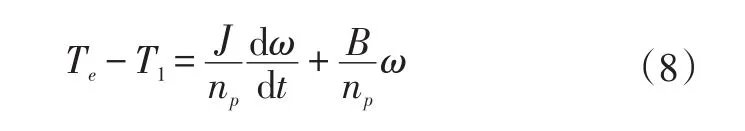
运动方程为：式中，ud、uq为d轴、q轴电压；Ld、lq为d轴、q轴自感系数；id、iq为d轴、q轴电流；ψd、ψq为d轴、q轴磁链；Mdf、Mqf为d轴、q轴互感系数；ω为永磁同步电机角速度；np为永磁同步电机极对数；Rs为定子绕组相电阻；B为阻力系数；if为永磁铁等效励磁电流；J为转动惯量；Te为电磁转矩；T1为负载转矩。

根据永磁同步电机数学模型，利用Matlab/Simulink建立相应的控制系统仿真模型，采用id=0的方法进行电机控制，该控制方法简单、计算速度快，故式（7）可描述为：式中，ψf为转子永磁体磁极的励磁磁链。

运行永磁同步电机Matlab/Simulink模型，图3为永磁同步电机输出转矩分别为90 N·m和10 N·m时的波形。

由图3可看出，永磁同步电机的转矩存在波动，定义转矩波动率为：

式中，Tmax为输出转矩最大值；Tmin为输出转矩最小值；T为额定转矩。

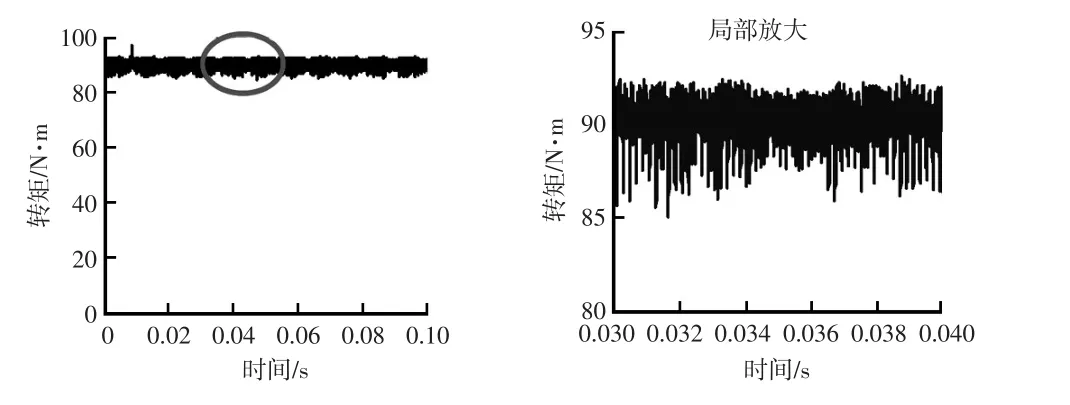
（a）输出转矩为90 N·m

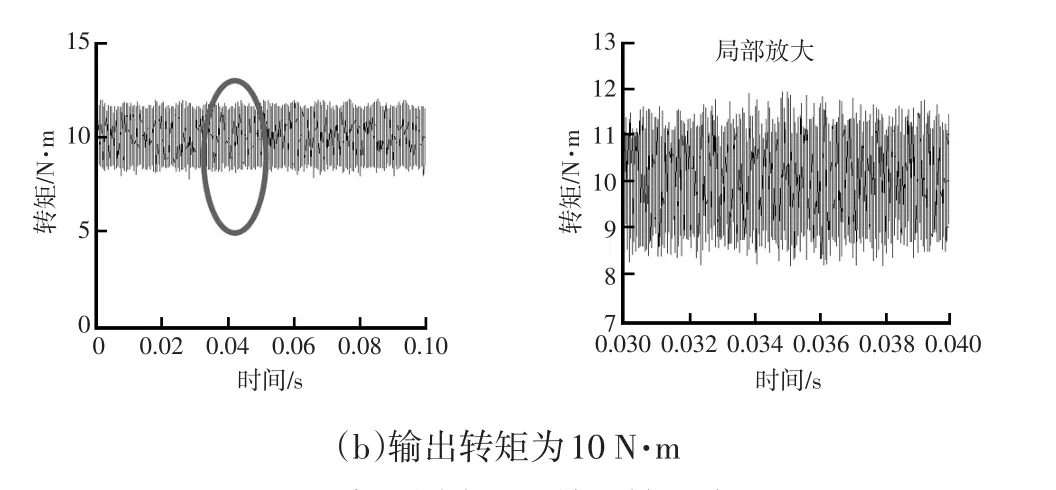
图3　永磁同步电机输出转矩波形

当输出转矩为90 N·m时，其转矩波动率为5 %；当输出转矩为10 N·m时，转矩波动率为20 %。由此发现，当输出转矩减小时，转矩波动率会随之增大。

3　分布式驱动电动汽车舒适性分析

3.1随机路面建模

汽车舒适性主要研究的是车辆对路面激励的响应。根据GB/T7301—2005的规定，在Adams中建立3D等效容积路面作为仿真分析路面。3D等效容积路面由一系列的空间三角形组成，基本元素为三角形平面和其所包含的节点坐标[9]。利用Matlab编写函数求出不同级别路面功率谱密度下的路面不平度数据，获得3D路面节点信息；将Matlab中提取的节点信息进行编号排列，指定摩擦因数。生成的B级3D随机路面模型如图4所示。

图4　B级3D随机路面模型

3.2汽车舒适性仿真

非簧载质量的增加对于分布式驱动电动汽车是不可避免的，它带来的车辆舒适性恶化在很多研究中得到确认，而转矩波动也是影响车辆舒适性的重要因素。采用Adams与Matlab/Simulink联合控制仿真模型（图5），其中，Simulink中输出的电机转矩作为Adams中车辆动力的输入，Adams中输出的车速作为Simulink中电机模型的输入。以传统带转矩波动的集中驱动电动汽车为参考，着重分析在两者共同作用下分布式驱动电动汽车的舒适性。

根据GB/T4970—2009的规定，舒适性随机路面输入选择B级随机路面，测量座椅座垫上方、座椅靠背、脚部地板3个方向的振动。试验车速分别为40 km/h、50 km/h、60 km/h、70 km/h和80 km/h。将各车速下测点的各向加速度进行加权计算，得到综合总加权加速度均方根值，计算式为：

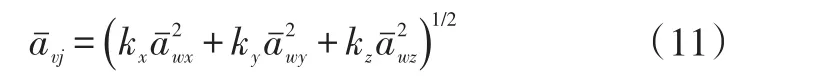
式中，

分别为各位置上x、y、z轴向的单轴向加权加速度均方根值；j=1，2，3分别代表座椅座垫上方、座椅靠背及脚部地板3个位置；

为各轴加权系数。

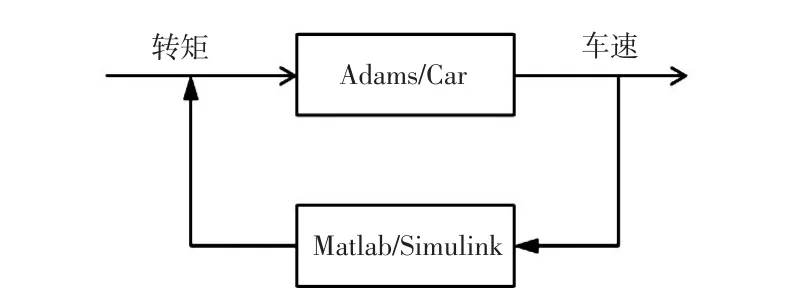
图5　Adams与Matlab联合仿真控制流程

式中，ωj为第j个1/3倍频带的加权系数，具体取值参见GB/T4970—2009；fj1、fj2表示第j个1/3倍频带的上、下限频率。

总加权加速度均方根值计算式为：

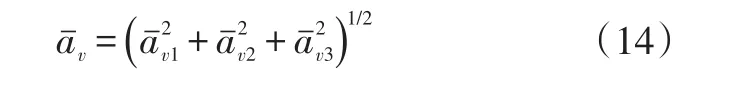
计算得到的各测点在各车速下的总加权加速度均方根值如表2所列。

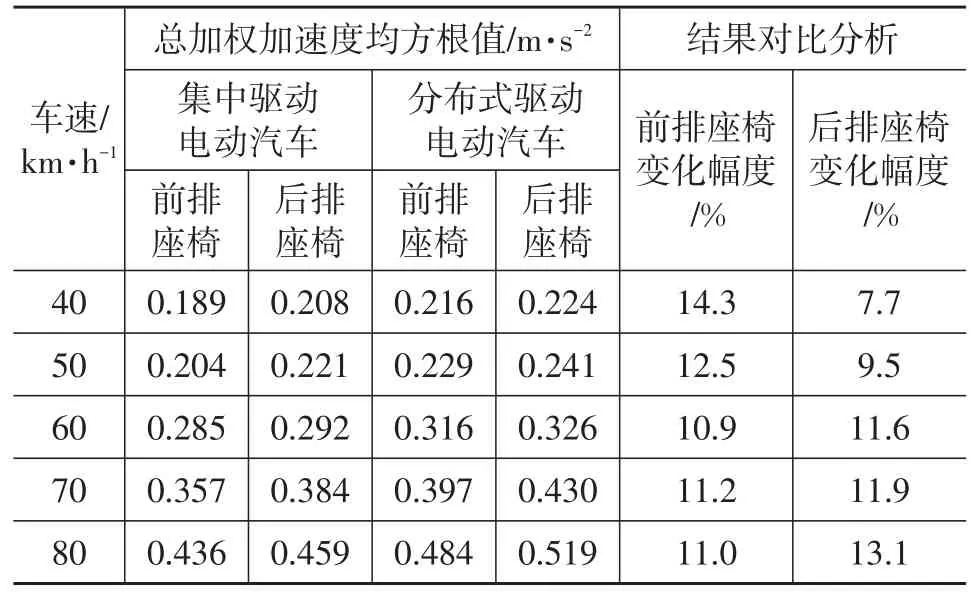
表2　不同车速下的总加权加速度均方根值

由表2可知，随车速的增加，分布式驱动电动汽车和集中驱动电动汽车的总加权加速度均方根值增加，车辆舒适性整体变差；分布式驱动电动汽车在所有车速下的总加权加速度均方根值均大于集中驱动电动汽车，且增加幅度范围为8 %～15 %。基于此，将对分布式驱动电动汽车舒适性进行多目标稳健性优化设计。

4　多目标稳健性优化设计

降低各种因素对质量性能的影响是稳健性优化设计的核心思想[10]。稳健性设计一方面注重产品的均值最优，另一方面要保证目标的方差最小。如图6所示，若不考虑不确定因素对性能的影响，最优解应选在点1处；当考虑影响因素的波动时，在点1处目标的变化量Δf1远大于点2处的变化量Δf2，对于稳健性设计来说，选择点2虽然会一定程度上牺牲产品的目标均值，但是却能使性能更加可靠。

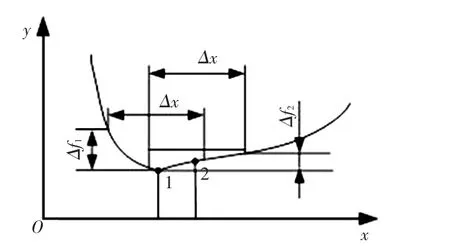
图6　确定性优化与稳健性优化的差别对比

稳健性优化设计的关键在于寻找“平坦的”设计空间范围，降低由于不确定设计参数引起的波动，构造包括响应目标值和方差在内的稳健性优化公式。

4.1目标函数

为提高分布式驱动电动汽车舒适性，以随机路面下汽车前、后排座椅总加权加速度均方根值为舒适性优化目标，同时为了控制不确定因素引起舒适性波动，以上述两个目标函数的统计方差σvf、σvr作为目标函数，即稳健性优化的目标函数为：

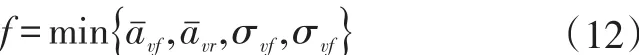
4.2设计变量

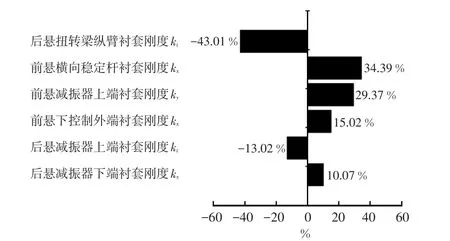
现代汽车大量使用衬套，在提高车辆舒适性的同时也带来了调校困难的问题[11]。本文选取前、后悬架连接处衬套的各向刚度为自变量，以前、后座椅总加权加速度均方根值为响应量，利用Adams/Insight模块完成DOE试验及灵敏度分析，其中自变量水平数为2，衬套刚度变化率为±10 %，灵敏度分析结果如图7所示。

（a）前排座椅

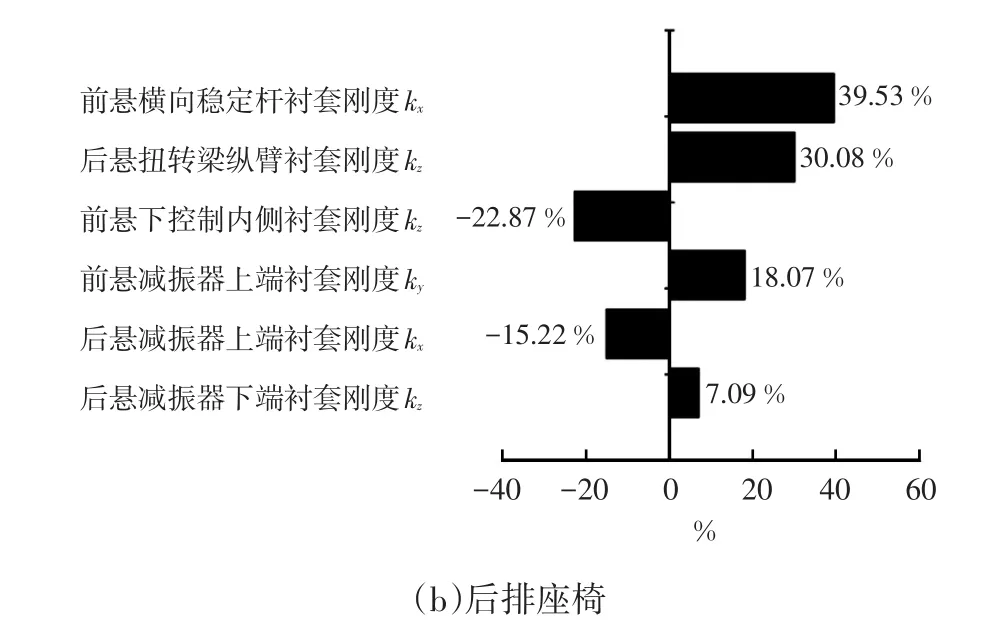
图7　前、后排座椅总加权加速度均方根灵敏度分析结果

根据灵敏度分析结果，选择前悬横向稳定杆衬套X向刚度（X1）、后悬扭转梁纵臂衬套Z向刚度（X2）、前悬下控制臂内侧衬套Z向刚度（X3）、前悬减振器上端衬套Y向刚度（X4）、后悬减振器上端衬套Z向刚度（X5）、后悬减振器上端衬套X向刚度（X6），以及前、后悬架的弹簧刚度k2f、k2r和阻尼系数c2f、c2r作为设计变量（由于前、后悬架弹簧和阻尼对车辆的贡献量很高，因此未对其进行灵敏度分析），各设计变量取值范围如表3所示。

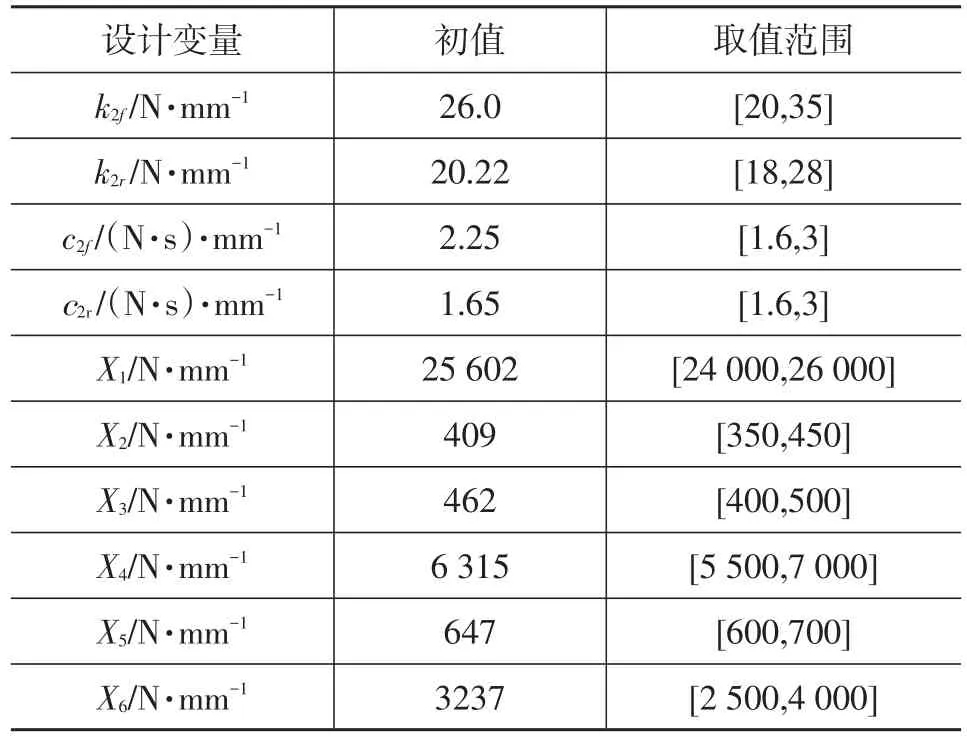
表3　设计变量取值范围

4.3不确定因素选取

分布式驱动电动汽车的动力由轮毂电机输出，不同车速下电机的转矩波动率不同，故将其作为一个不确定因素；同时，载荷变化会影响车辆的平顺性，因此将其也作为不确定因素。表4为转矩波动率和载荷状态的取值水平。

表4　转矩波动率与载荷状态的水平

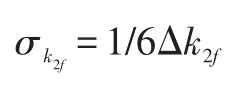
4.4响应面模型的建立

由于稳健性优化过程中需要同时考虑目标的均值和方差，计算量远大于确定性优化，为提高计算速度，采用响应面方法构造近似模型进行求解。通过拉丁超立方试验设计方法可获得试验样本点，采用二次多项式进行拟合，10个因素共有66个待定系数需要确定。为保证响应面模型的精度，从试验设计结果中选择120个样本点进行二次多项式响应面拟合，并用10个点对其进行模型的检验。

响应面模型的精度由复相关系数Ra2来评价，它是完全拟合的度量值，反映响应面符合给定数据的程度，其值越大，表示响应面的拟合精度越高[13]，工程上一般要求Ra2值达到0.9以上。通过对前、后排座椅总加权加速度均方根值进行检验，最后的拟合精度在0.91～ 0.94内，满足要求，因此可将该响应面模型作为近似模型进行稳健性优化。

4.5多目标稳健性优化

利用Insight和Matlab软件对响应面模型进行多目标稳健性优化，优化流程如图8所示。优化过程包括两个步骤，首先在不考虑稳健性的多目标模型中采用非支配排序遗传算法（NSGA-II）作为优化算法，算法参数设置为：种群规模数为20，繁衍代数为50，交叉概率为0.9，共仿真1 000次，得到590个Pareto解集，其结果如图9所示。然后对得到的每一组pareto最优解进行蒙特卡罗检验，通过考虑噪声因素来评价其稳健性，在所有pareto解中找到方差最小的稳健性好的解集，最终得到既优化又稳健的解[14]。

多目标稳健性优化前、后结果如表5所列。由表5可知，经过多目标稳健性优化后，分布式驱动电动汽车前、后排座椅处总加权加速度均方根值均有一定的减小，各车速下的优化百分比（优化前数值-优化后数值/优化前数值)达到10 %以上，有效提高了汽车的舒适性。

采用蒙特卡罗方法进一步分析稳健性优化结果。蒙特卡罗方法是一种利用重复的统计试验来求解物理和数学问题的方法，用随机过程来描述随机变量，统计得到均值以及方差分布[15]。采用简单随机抽样方法取400个抽样点得到稳健性优化前、后目标的概率分布如图10所示。

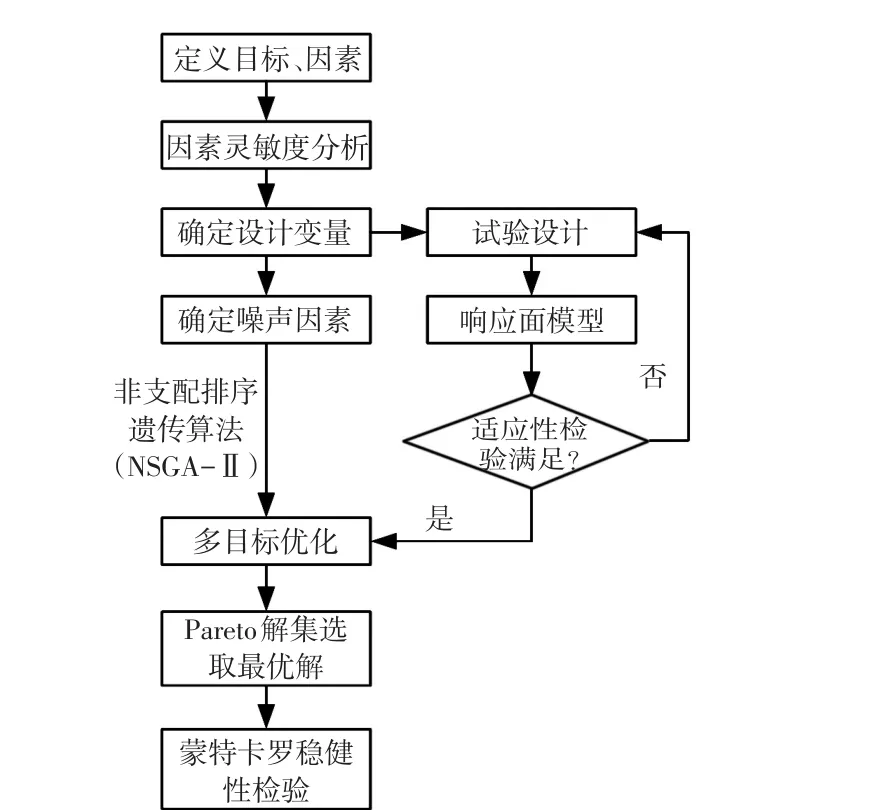
图8　多目标稳健性优化流程

图9　多目标稳健性优化结果

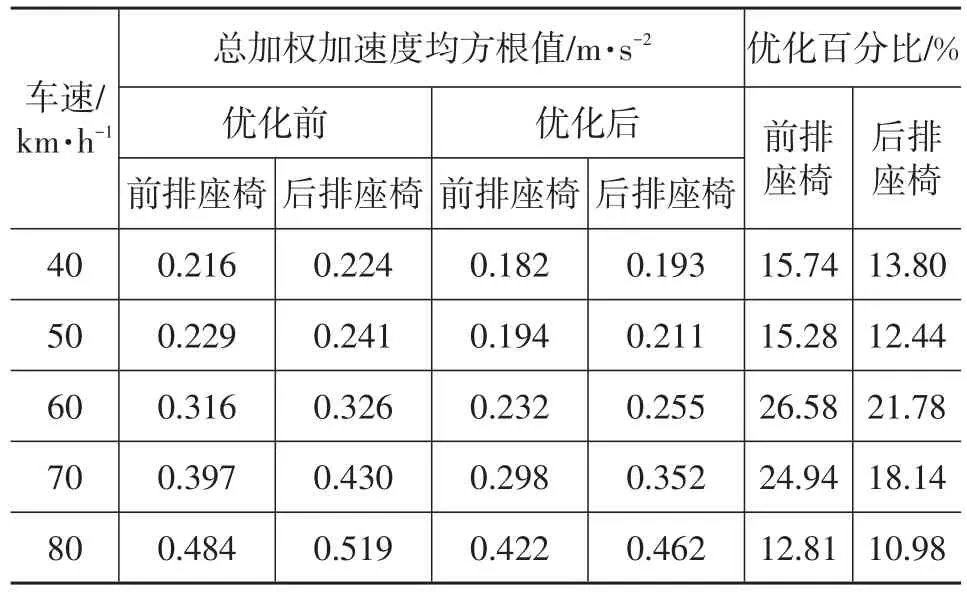
表5　多目标稳健性优化前、后结果

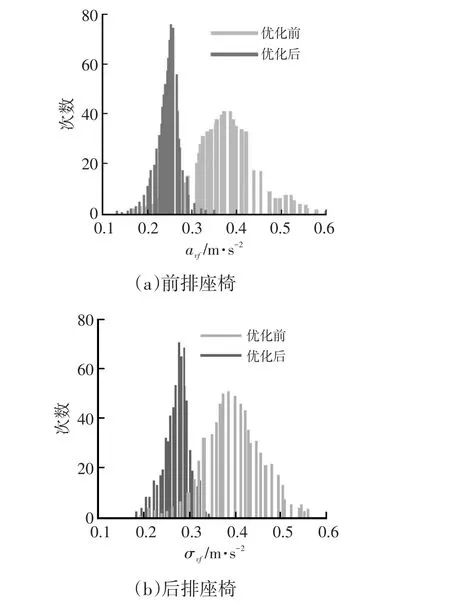
图10　稳健性优化前、后目标的概率分布

从图10可看出，进行稳健性优化后，前、后排座椅总加权加速度均方根值减小，并且方差也减小，表明在车辆舒适性提高的同时，由转矩波动、载荷变化以及弹簧、衬套制造误差等不确定性因素带来的汽车性能的波动也大大减小，车辆舒适性得到提高。

5　结束语

a.根据永磁同步电机数学模型及坐标变换原理，建立了分布式驱动电动汽车轮毂电机Simulink仿真模型。仿真结果表明，当电机输出转矩增大时，转矩波动范围增大，而波动率减小。在此基础上建立了ADAMS整车模型与Simulink永磁同步电机模型的联合仿真模型。

b.建立随机路面模型，对比分析了集中驱动与分布式驱动两款电动汽车的舒适性，通过分析驾驶员座椅各向加速度时间历程以及功率谱发现，分布式驱动电动汽车各测点处各向加速度峰值和总加权加速度均方根值均大于集中驱动电动汽车，表明由于非簧载质量的增加和转矩波动的引入，分布式驱动电动汽车舒适性有所恶化。

c.以转矩波动、载荷状态以及弹簧、衬套等制造误差为不确定因素，采用拉丁超立方试验设计构造响应面近似模型，运用多目标优化方法对分布式驱动电动汽车的舒适性进行了稳健性优化设计。优化结果表明，目标函数的均值和方差都减小，提高了分布式驱动电动汽车舒适性。

参考文献

1R Vos. Influence of in-wheel motors on the ride comfort of electric vehicles. Eindhoven University of Technology, 2010.

2 Anderson M, Harty D. Unsprung mass with in wheel motormyths and realities. AVEC10, Driver-Vehicle Control,2010: 261～266.

3智晋宁,项昌乐，朱丽君,等.轮边电机驱动汽车性能仿真与控制方法的研究.汽车工程, 2012, 34（5）, 389～393.

4 Maeda K,Fujimoto H，Hori Y. Four-wheel driving-force dis⁃tribution method based on driving stiffness and slip ratio es⁃timation for electric vehicle with in- wheel motors. 2012 IEEE Vehicle Power and Propulsion Conference,2012: 1286～1291.

5 JOÃO P C，GONÇALVES. Optimization of Vehicle Suspen⁃sion Systems for Improved Comfort of Road Vehicles Using Flexible Multibody Dynamics. Nonlinear Dynamics, 2003, 34, 113～131.

6 Zhou Zhibin, Xie Wei, Luc LORON. Torque ripple compen⁃sation in a non-sinusoidal permanent magnet synchronous motor. JOURNAL OF SHANGHA IMARITIME UN IVERSI⁃TY, 2009, 30（2）, 65～71.

7马琮淦,左曙光,杨德良，等.电动汽车用永磁同步电机的转矩阶次特征分析.振动与冲击,2013（13）:81～87.

8郭建波.分布式驱动电动汽车刚柔耦合建模及动力学分析：[学位论文].上海：同济大学, 2013.

9王涛,陶薇.考虑随机因素的汽车悬架参数多目标稳健优化.振动与冲击,2009（11）:146～149，210.

10陆建辉,周孔亢,郭立娜,等.电动汽车麦弗逊前悬架设计及参数优化.机械工程学报，2012, 48（8）：98～103.

11Prajakta Paluskar and Rohit Vaidya. Taguchi Method （DOE）Based Performance Optimization of a Three Link Rigid Axle Passenger Car Suspension Using MBD Simula⁃tions.SAE paper2011-10-4271.

12李铁柱,李光耀,陈涛，等.基于Kriging近似模型的汽车乘员约束系统稳健性设计.机械工程学报，2010，46 （22）:123～129.

13李程祎,左曙光,段向雷.考虑转矩波动的电动汽车悬架NVH性能参数优化.汽车工程,2013（4）:303～306，316.

14莫旭辉，赵宇航，钟志华，等.基于6σ稳健性方法的汽车行驶平顺性优化.中南大学学报（自然科学版），2012,43 （11）:4286～4292.

15谢展，于德介，李蓉.汽车发动机悬置系统的多目标稳健优化设计.汽车工程，2013（10）: 893～897.

（责任编辑文楫）

修改稿收到日期为2015年10月19日。

Robust Optimization of Electric Vehicle’s Ride Comfort with Consideration of Torque Fluctuation

Wu Guangqiang1,2, Zhang Ying1, Guo Qiang1（1.Tongji University, Shanghai 201804; 2.Institute of Industrial Science, University of Tokyo, Tokyo 153-8505）

【Abstract】For the problem of torque fluctuation and increased unsprung mass in distributed-drive electric vehicle, a vehicle rigid-flexible coupling model is established. Then in consideration of the non-sinusoidal distribution of magnetic field of permanent magnet synchronous motor, a Matlab/Simulink simulation model is established, which is used to study the effect law of torque fluctuation and unsprung mass on electric vehicle’s ride comfort. Based on the response surface approximation model, robust optimization is made to vehicle comfort with the multi-objective optimization method. The results show that after optimization, both the car’s ride comfort and reliability are improved.

Key words:Electric vehicle, Distributed- drive, Torque fluctuation, Unsprung mass, Ride comfort

中图分类号:U461.4

文献标识码:A

文章编号:1000-3703（2016）01-0013-06

*基金项目：国家重点基础研究发展计划（“973项目”）（2011CB711200）。

主题词:电动汽车分布式驱动转矩波动非簧载质量舒适性