基于因子分析的TOPSIS法改进对浅层地下水综合评价

2016-03-28苏建云黄耀裔李子蓉

节水灌溉 2016年1期

苏建云，黄耀裔，李子蓉

(泉州师范学院资源与环境科学学院，福建泉州 362000)

《地下水质量标准》(GB/T14848-93)[1]规定了地下水质量评价的指标体系、评价指标分级标准和内梅罗指数综合评价法，由此可见地下水环境质量评价是一种绝对性的综合评价，但由于评价指标的每一级仍存在质量的相对差异，因此也可以说是一种相对性综合评价。同时各指标不同级的区间值、不同指标同级区间值不同，在多指标的综合评价中作用、贡献程度(重要性)也不相同，于是衍生了从评价指标规范化变换角度提出的基于模糊数学隶属度的综合评价[2]、基于灰色关联度的综合评价[3]、基于“同异反”联系数的综合评价[4]、物元可拓法[5]、属性识别模型法[6]等地下水环境质量评价法及其从指标赋权角度提出的“超标”法[7]、“熵权”法[8]、“组合权重”法[9]等地下水环境质量评价法，极大丰富了地下水评价理论体系。

由于评价指标体系是表达系统构成的框架，其间难免存在相关性甚至多重共线性[10]，但是前述部分方法忽略了地下水评价指标体系指标之间必然存在这种关系——相关性甚至多重共线性(可通过SPSS软件的“KOM检验和Bartlett球形检验”等予以验证确认)。因此，本文提出通过因子分析[10]来有效克服评价指标间的相关性问题，通过对TOPSIS方法的改进、拓展达到能兼具绝对性评价与相对性评价的地下水综合评价的要求。以福建省晋江市浅层地下水为验证研究区，阐述方法的实施过程和效果，并对该区浅层地下水质量进行综合评价。

1 评价模型

1.1 评价指标及指标变换

1.1.1评价指标

设记：

(1)D1，D2，…，Di，…，Dn为待评对象(即实例中的福建省晋江市浅层地下水综合评价采样观测点的样品)，X1，X2，…，Xj，…，Xm为浅层地下水评价指标体系[1](选取总硬度、矿化度、硫酸根、氯离子、二价铁、二价锰、二价铜、二价锌、硝酸氮、亚硝酸氮、氨根、氟离子、二价汞、六价铬、碳酸氢根)共计15个评价指标构成评价指标体系，详见表1)。

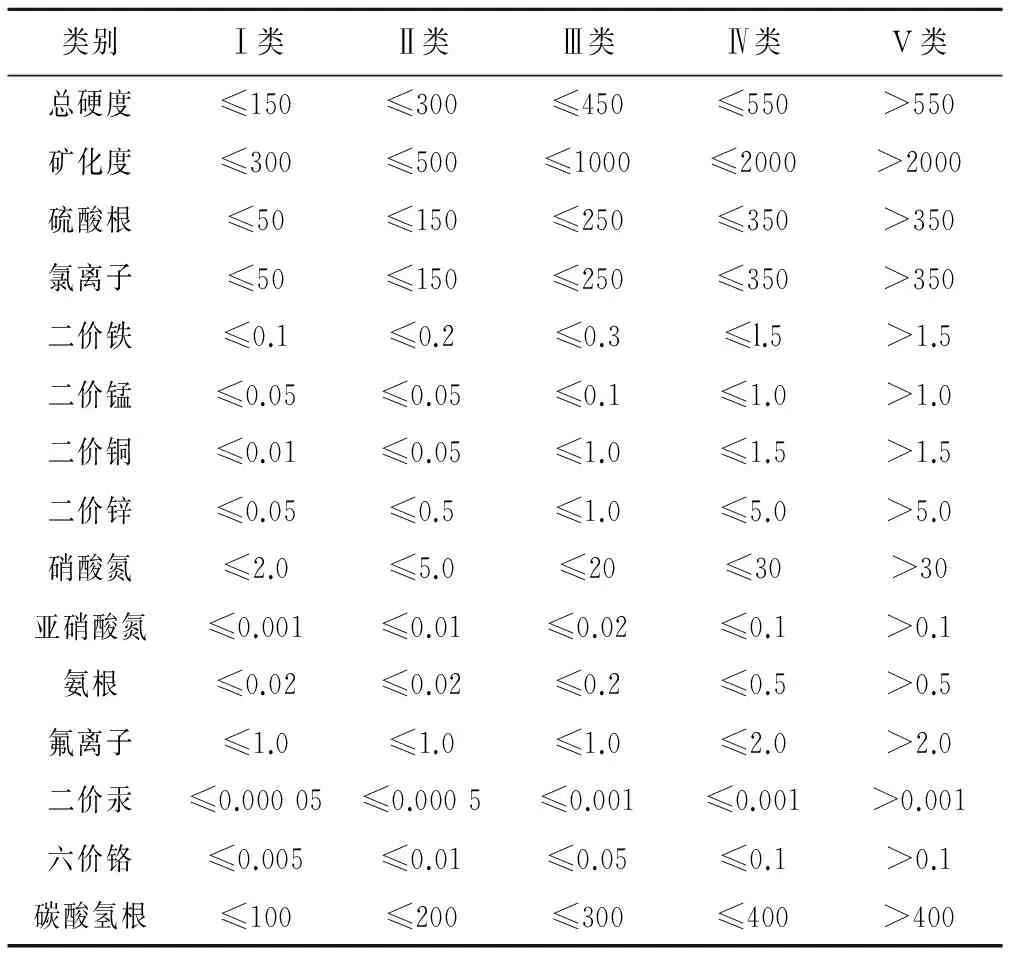
表1 地下水环境质量单项指标分类限值 mg/L

(2) [xi,j]n×m为决策矩阵(即浅层地下水综合评价采样观测点的样品D1，D2，…，Dn的化验测试结果)，其中xi,j表示Di(i=1，2，…，n)对象Xj(j=1，2，…，m)指标观测值(第i件水样第j个指标的分析测试结果)。

(3) [xl,j]L×m为地下水综合评价标准向量集即“标准点”、“控制点”、“已知点”的向量矩阵，xl,j(l=1，2，…，L；j=1，2，…，m)表示第l级标准j维分量Xj指标的上限(若是越大越好型的效益型指标则为下限)，分级标准可从《地下水质量标准》(GB/T14848-93)获取。

(4) [x+j]1×m、[x-j]1×m分别表示正(最优)、负(最劣)理想点的向量/矩阵，其中x+j、x-j分别表示正、负理想点第j维分量(Xj指标值)，式(1)和式(2)均包含成本型(越小越好)和效益型(越大越好)，且j=1，2，…，m。公式表示如下：

(2)

在此基础上对决策矩阵进行扩展，即通过合并决策矩阵[xi,j]n×m、标准向量矩阵[xi,j]L×m及理想点向量[x+j]1×m、[x-j]1×m得[xi,j]N×m(依次追加于[xi,j]n×m的n行之后，i=1，2,…，n+1，…，n+L，…，n+L+2 =N)，构造出新的决策矩阵。

1.1.2指标变换

(1)指标的标准化变换。对[xi,j]N×m按列进行标准化变换，记为[yi,j]N×m：

(4)

经式(3)与(4)变换后，[yi,j]N×m中各列指标均呈越大越好，其中，[xi,j]n×m→[yi,j]n×m、[xl,j]L×m→[yl,j]L×m、[x+,j]1×m→[y+,j]1×m、[x-,j]1×m→[y-,j]1×m。

(2)因子得分变换赋权。指标经标准化变换后，为了有效克服指标间难以避免的相关性甚至多重共线性，则需进一步通过式(5)进行变换：

F=[Fi,k]n×K=[yi,j]N×m[cj,k]m×K

(5)

cj,k的确定原则是Fk与Fp(i≠j) 相互独立(互不相关)，因子分析后的F1，F2，…，Fn依次是原变量所有线性组合中方差最大、次最大、…、第K大主因子。一般，[cj,k]m×K因子得分系数矩阵通过因子分析可得，则Fi,k为对象Di(i=1，2，…，n)在第k(k=1，2，…，K)主因子上的得分。本文以“累积方差贡献≥85%”为确定原则，对前述扩展、标准化变换后的[yi,j]N×m，利用SPSS软件进行因子分析，得到因子得分系数矩阵[cj,k]m×K见表2，提取3个主因子，占全部信息的87.24%>85%。将[yi,j]N×m、[cj,k]m×K(见表2)代入式(5)，则[yi,j]N×m变换为因子得分矩阵[Fj,k]m×K，相应的[yi,j]n×m→[Fj,k]m×K、[yl,j]L×m→[Fl,k]L×K、[y+,j]1×m→[F+,k]1×K、[y-,j]1×m→[F-,k]1×K。

1.2 综合评价

1.2.1综合评价模型

当前述[yi,j]N×m→[Fi,k]N×K后，因为“难以保证各公因子的因子得分都是越大越好或越小越好[10]”，如表2所示，F1因子得分系数均是大于0而维持了“越大越好”，但F2、F3的部分得分系数却小于0，可见F2、F3的因子得分未必是“越大越好”，所以，鉴于以往一些变换为因子得分的评价[11]因“根据公因子方差贡献直接进行因子得分的加权综合，按综合得分大小进行评序欠严密[10]”、与TOPSIS法综合的评价[12]或TOPSIS价值函数模型[13]是在变换为“因子得分”后才选择正、负基准/理想点的时机把握不准确[“因子得分”取大(“∨”、“max()”)或取小(“∧”、“min()”)未必与优、劣或劣、优一一对应]，须通过前述构建的正、负理想点作为识别的标准，于是提出基于因子得分变换的加权欧氏距离平方的TOPSIS综合评价模型。评价步骤如下。

表2 因子分析部分成果Tab.2 Some results of factor analysis

(1)首先计算各“待评点(含分级标准等)i”与正、负基准/理想点的加权距离：

(6)

(7)

式中：K表示第k主因子因子得分的权重(k=1，2，…，K)；λk为第k主因子的特征值，详见表2；Fi,k、F+,k、F-,k分别为待评点i及正、负理想点在第k主因子上的因子得分，见式(5)；d+i、d-i分别为待评点i与正、负理想点的加权欧氏距离，d+i越小、d-i越大则i越“优”，反之d+i越大、d-i越小则i越“差”。

(2)定义综合贴近度模型Di如下：

Di=(d-l-d+l)/(d-l+d+l)

(8)

式中：Di为待评点i与理想点的综合贴近度，Di∈[-1，1]，贴近度越接近1(正理想点)则越优，反之越接近-1(负理想点)则越差。

(3)因[Fi,k]N×K经[d+i]N×1、[d-i]N×1变换后为[Di]N×1，其中包括[Fl,k]L×K→[Dl]L×1、[F+,k]1×K→D+=1、[F-,k]1×K→D+=-1的变换，从而达到相对性综合评价(评序)，并为“绝对性”综合评价提供依据。即前述的数据准备已包含用于“绝对”评价分级分等的标准向量矩阵数据[xl,j]L×m，在前述的数据变换(准则替换)过程也同步进行了从原变量至综合贴近度的准则替换，即[xl,j]L×m→[yl,j]L×m→[Fl,k]L×K→[d+l]L×1+[d-l]L×1→[Dl]L×1，所以[Dl]L×1为综合评价等级划分的依据，详见表3。

表3 地下水评价分级准则Tab.3 Groundwater evaluation and classification criteria

1.2.2综合评价结果

根据表3的“绝对性”综合评价分级标准、[Fi,k]N×K及式(6)～式(8)得出晋江市浅层地下水综合贴近度[Dl]L×1及对应评价等级结果，详见表4。

参考相关评价文献大多仍采用基于离散点式数据评价，难以体现出空间分布状况，于是借助GIS手段结合地统计模型构建浅层地下水环境综合质量评价数字地面模型，采用Kriging插值[14，15]将离散的评价等级结果连续化表达和可视化(见图1)。

1.2.3综合评价结果分析

基于因子得分变换的加权欧氏距离平方的TOPSIS综合评价与单纯利用TOPSIS法的评价结果吻合率达到90%。单纯利用TOPSIS法的权重确定是事先确定的，具有一定的主观性和随意性，比较适合对区分最优、最劣2级的评价。而基于因子得分变换的加权欧氏距离平方的TOPSIS采用了方差贡献率表征,当方差越大的指标则重要程度则相对较大,故权重也应较大,对权重的确定较具客观，同时TOPSIS对原始数据进行趋同和归一化,通过《地下水质量标准》构建了正、负理想点作为识别的标准，使分类精度得到提高，通过因子得分变换保证各公因子的因子得分统一为“越大越好”或“越小越好”。从同一指标与最优指标的加权欧氏距离计算出体现同一指标间的接近度,能兼具绝对性评价与相对性评价来反映出地下水综合评价的要求。说明通过因子得分变换的方差贡献率作为权重，分类精度也比较高，评价结果也更为合理。

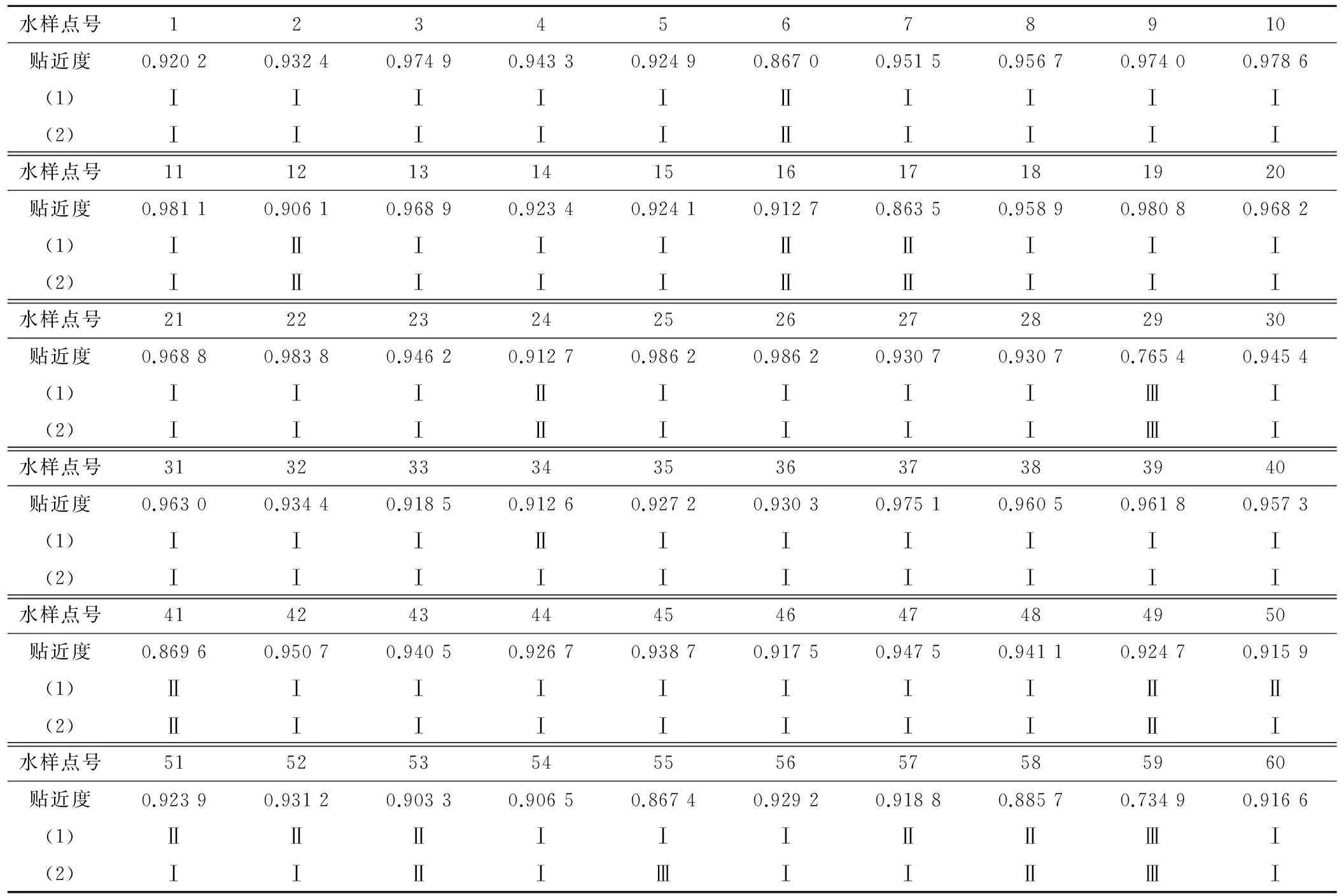
表4 晋江市浅层地下水综合评价等级结果Tab.4 Comprehensive evaluation results of shallow groundwater in Jinjiang City

注：(1)为基于因子得分变换的加权欧氏距离平方的TOPSIS评价结果；(2)为单纯利用TOPSIS法的评价结果。

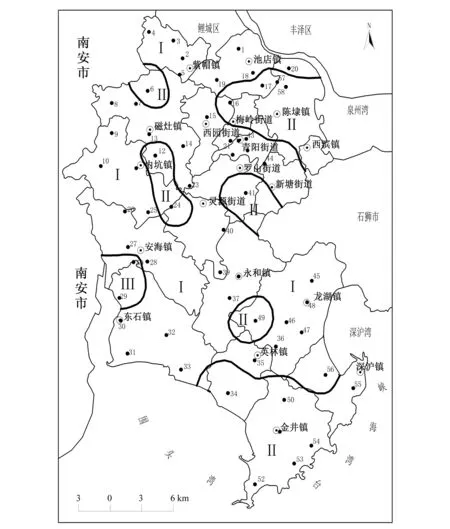
图1 浅层地下水评价数字地面模型Fig.1 Shallow groundwater evaluation of digital terrain model

据图1所示，评价结果处于地下水Ⅲ级水平(以人体健康基础值为依据，使用于集中式生活饮用水源及工、农业用水)主要分布于境内的安海镇、东石镇与南安市的石井码头临界；评价结果处于地下水Ⅱ级水平(反映天然背景值)主要分布于境内的陈埭镇、西滨镇与泉州湾邻接，深沪镇、金井镇与台湾海峡、围头湾邻接的大部分区域，灵源街道、新塘街道与石狮市邻接，永和镇、龙湖镇、英林镇三镇交接，内坑镇、磁灶镇部分区域；其余为Ⅰ级(反映天然低背景值)。处于地下水Ⅰ、Ⅱ级水平占全区面积的96%左右，通过基于因子分析的加权欧氏距离平方的TOPSIS对晋江市的综合评价，评价结果整体处于良好水平。

2 结语

本文提出了通过因子得分变换来有效克服评价指标间的相关性甚至多重共线性问题，及通过对TOPSIS方法的改进、拓展达到能兼具绝对性评价与相对性评价的地下水综合评价的要求。将其应用于福建省晋江市浅层地下水质量环境的综合评价，通过GIS和地统计的Kriging插值构建浅层地下水环境质量评价数字地面模型，使评价等级结果可视化表达。通过基于基于因子得分变换的加权欧氏距离平方的TOPSIS对晋江市的综合评价，评价结果整体处于良好水平，可为晋江市今后在对浅层地下水的合理开发利用以及保护提供参考。

[1] GB/T14848-93，地下水质量标准[S].

[2] 苏建云，黄耀裔．修正的模糊数学综合评判法在地下水环境质量评价中的应用——以福建省晋江市为例[J]．西南师范大学学报(自然科学版)，2014，39(7)：78-85．

[3] 黄耀裔．基于灰色关联度变权法的浅层地下水环境质量综合评价[J]．节水灌溉，2015，(1)：43-47．

[4] 张泽中，齐青青．集对分析综合评价方法的改进及其应用[J]．节水灌溉，2010，(10)：16-19．

[5] 黄耀裔．改进的物元分析法在浅层地下水综合评价中的应用[J]．西北师范大学学报(自然科学版) ，2014，50(6)：92-98．

[6] 郭凤台，王瑞京，孙红．属性识别模型在黑龙洞泉域地下水质评价中的应用[J]．节水灌溉，2008，(11)：43-45．

[7] 张岩祥，肖长来，刘泓志，等．模糊综合评价法和层次分析法在白城市水质评价中的应用[J]．节水灌溉，2015，(3)：31-34．

[8] 丁丽宏．基于熵权与灰色关联法的引水方案评价研究[J]．节水灌溉，2012，(10)：56-59．

[9] 李秋元，刘东．组合权重模糊模型在区域地下水水质评价中的应用[J]．中国农村水利水电，2014，(3)：1-5．

[10] 陈文成．基于因子分析的区域经济不平衡发展研究[J]．数理统计与管理．2010，29(3)：490-501．

[11] 张伟．基于因子分析的安徽省水资源承载力评价[J]．节水灌溉，2012，(9)：11-14．

[12] 赵玲萍，张凤娥，董良飞，等．改进的熵权TOPSIS模型在农村生活污水处理优选中的应用[J]．节水灌溉，2013，(12)：52-55．