河南省先进制造业自主创新评价指标体系
2016-03-28张地郑州大学商学院河南郑州450001
张地(郑州大学 商学院,河南 郑州 450001)
河南省先进制造业自主创新评价指标体系
张地
(郑州大学商学院,河南郑州450001)
摘要:先进制造业是制造业的发展方向和前景,自主创新能力是先进制造业持续发展的关键因素.本文通过选取了先进制造业创新能力的四个主要方面和13个具体指标,采用层次分析法对河南省先进制造业的自主创新能力水平进行了综合评价分析.
关键词:自主创新;制造业;层次分析法
先进制造业代表着制造业的技术发展方向和技术的领先水平,它不仅是科技进步的产物,也是时代发展的必然.先进制造业的核心表现就是自主创新研发能力,它是制造业科技水平的持续领先的动力和源泉,也是制造业先进产品不断进步的保证.构建先进制造业创新能力评价指标体系,对于河南省当前的制造业发展具有长远的意义和作用.
1河南省先进制造业自主创新能力评价指标体系构建
自主创新能力是多种因素促成的结果,其评价指标体系也是一项系统、科学、合理、有针对性的指标因素群.结合河南省先进制造业发展的实际情况和相关文献研究,笔者设定了四项创新能力考核方面,分别是创新投入能力、创新产出能力、创新核心因素和创新环境因素.并结合科学性、可比性、实际性和合理性的原则指导,初步选取了21个指标因素.在相关专家学者的指导下,去掉了代表性不强、主观性过高和数据不够充分的8个指标,保留了13个指标来综合分析先进制造业自主创新能力的水平(见图1).

图1河南省先进制造业自主创新能力评价指标体系
2河南省先进制造业自主创新能力评价指标模型构建
2.1层次分析法简介
层次分析法是由美国著名的运筹学家匹兹堡大学的A. L.Saaty教授于20世纪70年代提出的一种决策方法.它是将评价对象或问题视为一个系统,根据问题的性质和想要达到的总目标将问题分解成不同的组成要素,并按照要素间的相互关联度及隶属关系将要素按不同层次聚集组合,从而形成一个多层次的分析结构系统,把问题条理化、层次化.
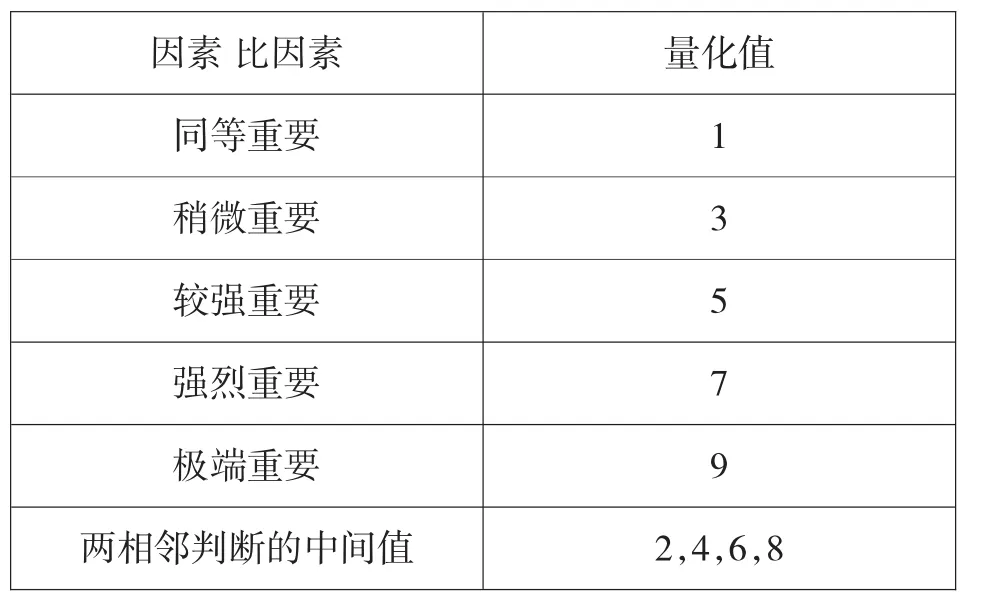
图2层次分析法中的1-9测度法
层次分析法是通过两两比较判断的方式来确定每一层次中要素因子的相对重要性,然后根据相对的水平指标在递阶层次结构内部合成后得到了重要程度的总排序.层次分析法的简便有效得到了多数研究学者的亲睐.它的优点十分鲜明,解决多层次、多指标的递阶结构问题十分见效,而且将定性分析与定量分析有效结合,避免了主观判断的臆测性和过于追求数据的理论性.但层次分析法采用的是1-9测度法,由专家学者结合自身了解和相应数据给出直观判断,在重要性对比程度中,会出现测度不够精确的情况.但对于本文的分析,层次分析法是完全可行的.
2.2自主创新能力评价指标模型
按照图1建立起来的层次分析模型,结合定性和定量方法构建起来判断矩阵,并确定相应权重.笔者邀请了若干名专家、学者、研究人员和企业家各自对评价指标体系中的因子指标按照“1-9测度法”给出相对应的标度,并计算出了相对应的指标权重.其次,对专专家、学者、研究人员和企业家评价指标得出的权重进行加法总和求平均方法,确定各项因子指标的最终权重值.例如,假设共邀请了N名专家、学者、研究人员和企业家,对于每一个因子指标Ci(i=1,2,3 …)给出的权重为Ki(i=1,2,3…,n),因子指标Ci的最终权重等于按照专家、学者、研究人员和企业家打分的结果,构建出判断矩阵,计算得出层次单排序好层次总排序,并得到目标层的权重比纸Ai(i=1,2,3…n).根据河南省先进制造业的发展规模、现状等具体情况,依据相应人员的打分,并采用加权平均方法得出中间层B的各个权重Bi(i=1,2,3…n).

3 模型应用
河南省先进制造业自主创新能力评价指标体系的确立是为了充分检验河南省当前先进制造业自主创新的水平和层次.本文共为10位专家、学者、研究人员和企业家发放了层次分析判断研究材料,最终收回9份有效数据.笔者为上述人员提供的数据主要是来自《河南省统计年鉴2014》《中国统计年鉴2014》、河南统计网等,均为评分人员提供了相对比较新的和有代表性的统计数据.
3.1中间层和因子层判断矩阵的处理和权重系数
首先,按照专家人员的打分结果,在判断矩阵输入各项评分值,并设定了基础性一致性,在得到计算结果后,根据yahhp的软件反馈的意见对判断矩阵进行了有针对性的修正,得到了最终的判断矩阵和计算结果.
通过对各层次矩阵按照层次分析法的一般流程进行分析、处理,得到了判断矩阵的系列结果.见图3,表1,表2,表3,表4,表5.
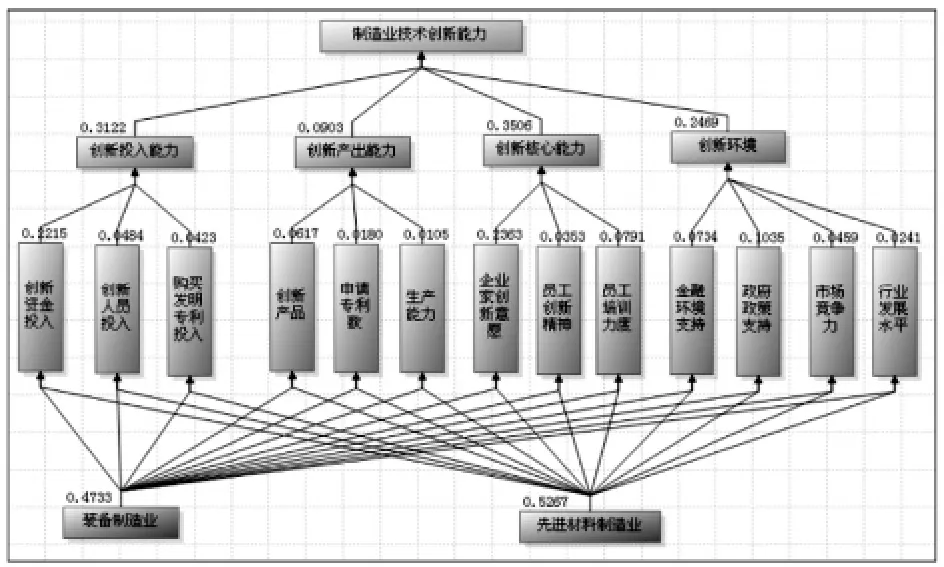
图3制造业技术创新能力
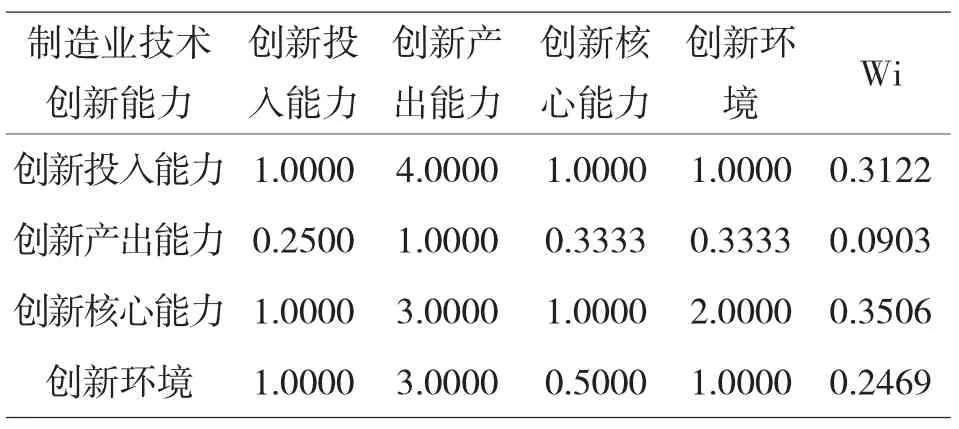
表1目标层A的一致性比例、权重和特征向量
1.制造业技术创新能力一致性比例:0.0266;对“制造业技术创新能力”的权重:1.0000;λmax:4.0710

表2中间层B1的一致性比例、权重和特征向量
2.创新投入能力一致性比例:0.0176;对“制造业技术创新能力”的权重:0.3122;λmax:3.0183

表3中间层B2的一致性比例、权重和特征向量
3.创新产出能力一致性比例:0.0236;对“制造业技术创新能力”的权重:0.0903;λmax:3.0246
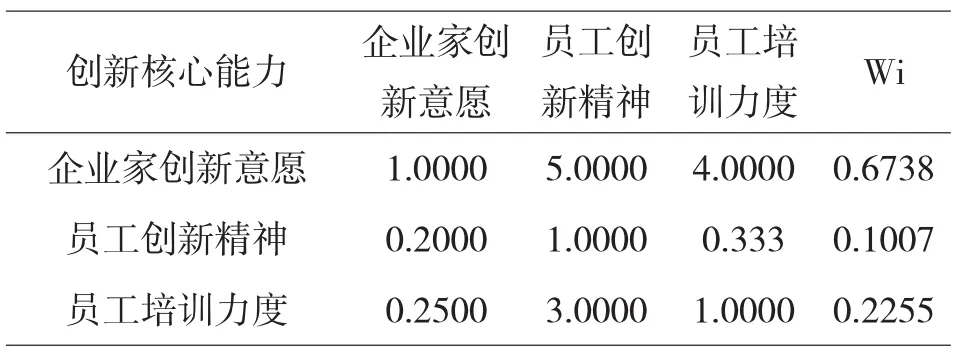
表4中间层B3的一致性比例、权重和特征向量
4.创新核心能力一致性比例:0.0825;对“制造业技术创新能力”的权重:0.3506;λmax:3.0858

表5中间层B4的一致性比例、权重和特征向量
5.创新环境一致性比例:0.0882;对“制造业技术创新能力”的权重:0.2469;λmax:4.2354
3.2一致性检验
一致性检验按照以下三个步骤进行:
(1)计算一致性指标CI=(λmax-n)/(n-1);(2)找出相应的平均随机一致性指标RI;(3)计算一致性比例CR=CI.
CI值可以较为清楚地反映出来判断矩阵各层次非一致性的程度,但是却没有指明非一致性是否能接受.所以,在具体分析非一致性的可接受问题时,还需引入一项衡量的标准值.即所谓随机一致性指标,根据平均随机一致性指标(RI)来计算随机一致性比率:CR=CO/RI.一般来说,当CR<0.1时,认为此项判断矩阵基本符合随机一致性指标;当CR≥0.1时,认为判断矩阵不符合随机一致性指标,必需进行调整和修正,使其满足CR<0.1,从而具有满意的一致性.
关于平均随机一致性指标的值,用的比较多的是Satty教授按照1阶~15阶重复计算1000次得到平均随机一致性指标.一般文献上仅给出了Satty已计算好的1阶~9阶矩阵的RI值表,但均未给出实现过程,本位引用的平均随机一致性指标如下表6:
表1:目标层A的一致性检验

表6 1阶~15阶平均随机一致性指标表
本文将“一致性检验”与“层次单排序”和“综合排序”同步进行,计算得到λmax=4.0710,当n=4时,λmax略大于n.
可得RI=0.89,CI=(λmax-n)/(n-1)=0.027.
CR=CI/RI=0.0263<0.1,对于其它的每个判断矩阵,其CR都满足CR<0.1,则该矩阵具有满意的一致性.因此,其不一致性可以被接受.
以此类推,可得出其余各目标层的CR数值(保留小数点后三位).
表2的一致性检验中,RI=0.52,得出CR=CI/RI=0.018<0.1
表3的一致性检验中,RI=0.52,得出CR=CI/RI=0.024<0.1
表4的一致性检验中,RI=0.52,得出CR=CI/RI=0.082<0.1
表5的一致性检验中,RI=0.89,得出CR=CI/RI=0.088<0.1
当CR<0.1时,判断矩阵的不一致性程度在容许的范围之内,此时可以用A、该判断矩阵的特征向量作为权向量.可见,自主创新能力体系的目标层和中间层得出的一致性比例检验均符合层次分析法的判断标准,均在有效范围之内.
3.3模型矩阵结果分析
按照上图中得到的中间层对于目标层的权重结果,权重的大小分别为:B1=0.3122,B2=0.0903,B3=0.3506,B4=0. 2469.同时,按照权重大小排序,得到的次序从高往低分别是,创新核心能力、创新投入能力,创新环境和创新产出能力.分析得出,创新核心能力和创新投入能力在制造业自主创新中具有较为重要的意义,而要激发制造业创新的动力和活力,首先要考虑从创新核心能力和创新投入能力上采取相应措施来激发制造业企业的生产潜力.
其次,在B3矩阵中企业家创新意愿的权重Wi达到0.6738,远高于员工创新精神0.1007和员工培训力度0.2255,所以企业家创新意愿又凸显的尤为重要.在B1矩阵中,创新资金投入也是远高于创新人员投入和购买发明专利投入,创新资金对于企业研发创造的意义具有根本性的重大意义,只有拥有充分的创新资金、研发资金,企业家的创新点才能得以投入和实施,企业的研发项目才能得以保证正常进行,才能抗的住研发失败的风险,最终掌握住核心科技动力,依托高科技实现企业的成功转型升级.在B4矩阵中,政府政策支持权重Wi达到0.4193,金融环境支持权重达到0.2974,市场竞争力权重达0.1858,行业发展水平权重达到0.0975.在当前环境,尤其是制造业大型行业范围内,政府政策支持,金融环境支持对于制造业创新的意义也是极为重要的.制造业事关国家经济重要领域,制造业的前景必须通过创新来实现,而制造业的综合水平和实力也是创新研发的具体表现,只有政府的大力支持帮助,政策引导,金融行业的资金支持,才能帮助制造业顺利走上技术创新、研发自主的成功道路.
参考文献:
〔1〕张勤,李成标.湖北省制造业技术创新能力评价[J].科技创业,2010:97.
〔2〕崔颖.基于层次分析法的河南科技创新人才创新能力评价研究[J].科技进步与对策,2012,29(6).
〔3〕孔金生,吴丽娟.河南省装备制造业技术创新的影响因素分析,2009(9).
〔4〕焦树锋.AHP法中平均随机一致性指标的算法及MATLAB实现[J].太原师范学院学报(自然科学版),2006(12).
〔5〕杨楠.河南省高新技术产业自主创新能力评价[J].科学管理研究,2012(2).
收稿日期:2015年11月17日
中图分类号:F204
文献标识码:A
文章编号:1673-260X(2016)01-0087-03
