考虑时空特性分布的电动汽车充电负荷预测
2016-03-27冯耀轩邓文雄盛鹏飞
王 森,冯耀轩,邓文雄,周 刚,盛鹏飞
(国网浙江省电力公司嘉兴供电公司,浙江 嘉兴 314000)
考虑时空特性分布的电动汽车充电负荷预测
王 森,冯耀轩,邓文雄,周 刚,盛鹏飞
(国网浙江省电力公司嘉兴供电公司,浙江 嘉兴 314000)
随着电动汽车的快速推广应用,对电动汽车充电负荷需求实现较准确的预测也逐步成为电动汽车领域研究的热点。为解决电动汽车大量推广应用后的电网负荷平衡问题,在分析电动汽车时空特性分布的基础上,提出了一种基于自适应动态三次指数平滑法的电动汽车负荷预测模型。该预测模型对传统的三次指数平滑模型进行改进,并根据误差绝对值之和最小的原则及时调整,以获得理想的平滑系数,再对后续的年度最大日电动汽车充电量和不同小区的典型日电动汽车充电负荷进行预测。以某工业小区和居民小区电动汽车负荷分布为例进行仿真,仿真结果表明所提方法误差较小,给出的充电桩规划建议也切实可行。
电动汽车;负荷平衡;时空特性;自适应;负荷预测
0 引言
近年来,电动汽车因其良好的环保和节能特性成为最有发展前景的交通工具[1]。电动汽车的充电负荷具有很强的随机性、间歇性和波动性,而这又是由规模化电动汽车充放电的随机性决定的。因此,有必要对电动汽车负荷进行预测研究,及时根据电动汽车负荷分布的时空特性,合理地对充电桩进行布点规划。对电动汽车充电负荷进行有效的预测不仅有利于电网因地制宜的规划,还利于调度部门适时调整调度计划,降低电网运行成本,减少对环境的污染。
在国家对电动汽车的鼎力支持下,电动汽车充电桩的布局已成为电动汽车领域的研究热门[2]。目前,海内外专家学者有针对性地在这方面做了许多深入的研究,并提出了多种电动汽车负荷预测方法和充电桩规划方法[3,4]。这些方法在一些特定的研究范围有很好的应用,但鲜有考虑电动汽车负荷时空分布的随机性和不同时间段的历史负荷数据对预测结果的影响大小,以至于影响了电动汽车充电负荷的预测效果。
结合电动汽车充电负荷的时空特性分布,提出一种基于自适应动态三次指数平滑法[5]的电动汽车负荷预测模型,对电动汽车的年度最大日充电电量和典型日的负荷进行预测,并给出了电动汽车的充电桩规划布局建议,充分验证了所提方法的有效性。
1 三次指数平滑法预测模型
指数平滑法是一种特别的加权平均方法,将数据由远及近分类,而且越近的数据对预测值的影响越大。指数平滑法正是考虑了远近期数据对预测值的影响不同这一特点,并按指数递减的规律分配权值,越近的数据,所分配的权重越大;反之,越远的数据,所分配的权重也就越小。根据平滑的次数将指数平滑法分类,通常使用的有一次指数平滑法、二次指数平滑法和三次指数平滑法。但一次指数平滑法适用于对没有明显趋势效应或呈平滑趋势的时间序列进行分析和预测,而对线性变化的时间序列进行预测多采用二次指数平滑法。因为电动汽车充电负荷变化的随机性大,呈明显的非线性变化趋势,所以选择三次指数平滑法来预测也是顺理成章的[3]。
三次指数平滑模型是对电动汽车充电负荷进行一次指数平滑后再进行两次平滑才获得的。其平滑公式为:
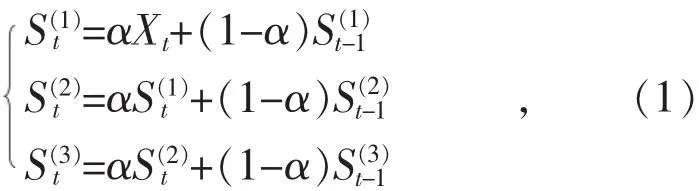
第(t+m)期的预测值计算公式为:
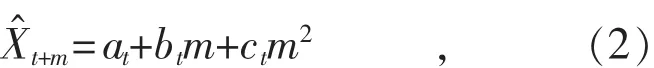
式中:m为预测步长,即预测数据的期数与当前期数的差值,取正整数,如m=1即为一步预测;另外记其中预测参数见式(3)。
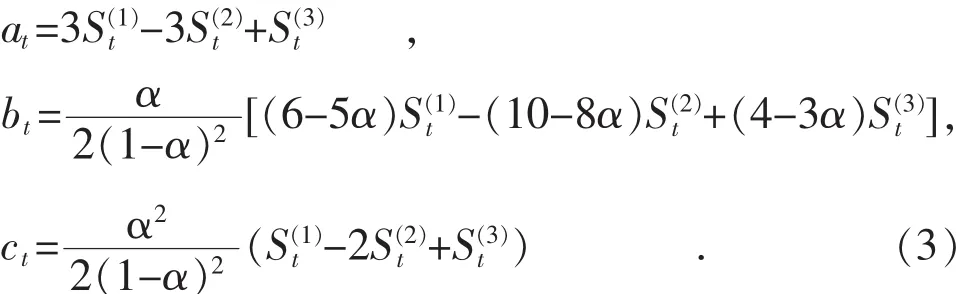
通常采用以下2种方式确定平滑初值:
(1)当数据量比较大的时候,预测值受平滑初值的影响很小,因此选取
(2)当数据量较小时,预测值受平滑初值的影响比较大,取前面若干数据的简单算术平均数作为初值,如等。
平滑系数α的大小主要表现为不同时期电动汽车历史充电负荷数据在指数平滑模型中所占比重大小,即根据观测到的历史充电负荷数据对预测值的影响大小,按其远近分配不同的权重值。越靠近当前要预测的目标充电负荷数据,分配的权重越大;离当前要预测的充电负荷数据越久远的数据,分配的权重越小,即“重近轻远”的原则。其中,α值越大,如果历史充电负荷数据越靠近预测值,则对当前的预测值影响越大,权重变化得越快;相反,α取值越小,权重变化就越慢,对预测值的影响甚微,预测值越靠近算术平均值。由此可以看出:平滑系数α取不同的值对三次指数平滑模型的预测效果影响很大,选取恰当的平滑系数将是建立三次指数平滑模型的重要环节。预测值与实测值的误差越小,效果越好。当充电负荷预测值与实测值间的误差最小时,即达到了最理想的预测效果。依据这一原则,选取不同的α,并根据该值计算误差绝对值之和,当误差绝对值之和最小时,α为理想系数。
按式(4)求取最小误差绝对值之和:
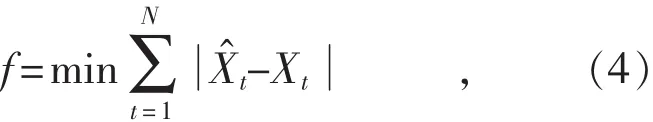
2 自适应的动态三次指数平滑法模型
在传统的三次指数平滑法中,平滑系数α确定后即以常数的形式参与平滑过程,平滑模型不能很好地随着时间序列的变化而变化,对后期的平滑预测效果也不是很理想。基于以上不足,可以考虑对该方法进行改进。下面提出一种带有动态平滑系数的指数平滑模型,该模型可以提高电动汽车负荷的预测精度,还能增强电动汽车负荷预测的可靠性。
将传统的三次指数平滑模型的各项系数作归一化处理,并做出合适的展开,按式(5)即可算出平滑系数:
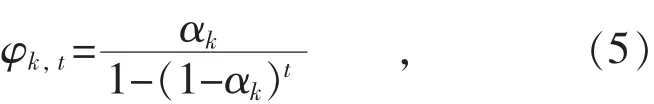
式中:k为预测的次数,k∈N*;将第k次的自适应平滑系数记为αk,αk∈(0,1);当t>1时,φk,t∈(0,1),符合平滑系数的条件。显然φk,t是关于时间t的函数,故可选取φk,t为动态的平滑系数。
令Xk,t=Xk+t-1;t=1,2,…,N;N为每次预测时选取历史电动汽车负荷数据的期数。在三次指数平滑法的基础上,因 αk,φk,t能伴随预测次数的变化而动态改变,则基于自适应的动态三次指数平滑法的电动汽车负荷预测模型如式(6)所示:
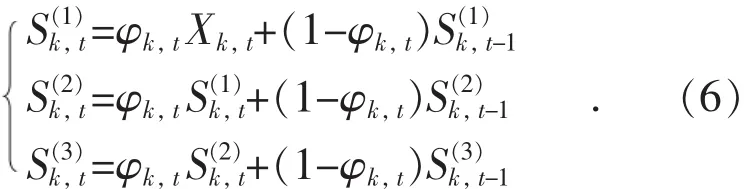
新的电动汽车充电负荷预测公式为:
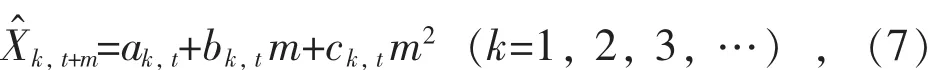

此外,当t=1,2时,每一次电动汽车负荷预测值都取所选取N期数据的初值,即
采取地毯式遍历搜索的方法确定每一次的平滑系数αk[8],求出对应的误差绝对值之和f的值。当误差绝对值之和f最小时,所对应的αk即是当次的最佳平滑系数,后续的平滑系数确定过程与此类似。为了提高预测效果和预测精度,每次选取平滑系数的步长都可以尽可能地小。
按式(9)确定每次自适应的平滑系数αk:
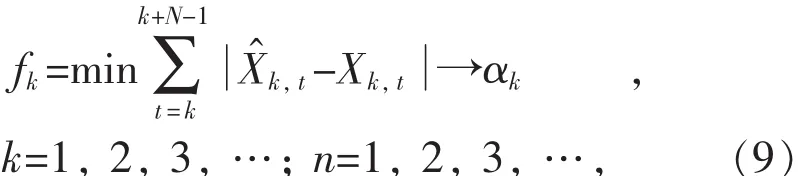
用前n期负荷数据并根据上述公式确定出平滑系数αk,进而利用自适应的三次指数平滑法预测第(k+n+m-1)期的数据。
用N替换t,代入式(7)和式(8)即可得到最终的预测公式:
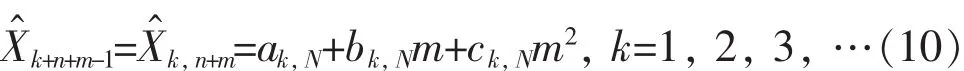
自适应动态三次指数平滑法的预测流程如图1所示。
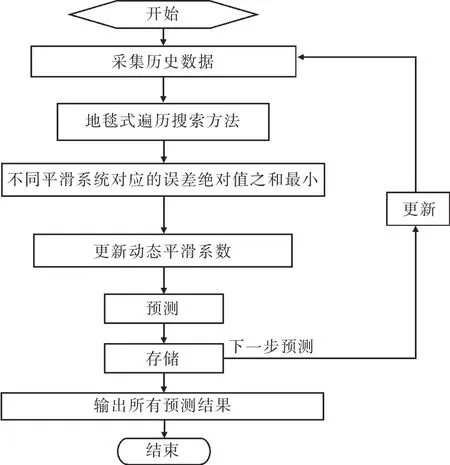
图1 自适应动态三次指数平滑预测流程
3 电动汽车负荷分布的时空特性分析
电动汽车充电负荷预测和充电桩的规划布局不仅需要考虑充电需求的空间分布,还要考虑电动汽车充电时间、续航里程等[6-11]。因此电动汽车负荷分布的时空特性对充电负荷预测和充电桩的规划起着至关重要的作用。
3.1 电动汽车负荷分布的空间特性
各区域的经济基础、人口密度、地理位置不同,直接影响该区域的车流量,对电动汽车充电桩的规划起着至关重要的作用。文中只考虑2个典型区域电动汽车的空间负荷分布特性,即典型居民区和典型工商业区。对某地区居民区停车需求的调研结果如表1所示。
表1中的停车需求率是指该时段的停车需求与最大停车需求的比值。对表1中的数据进行拟合,得到典型居民区t时刻的停车需求率函数P*(t)如式(11)所示。
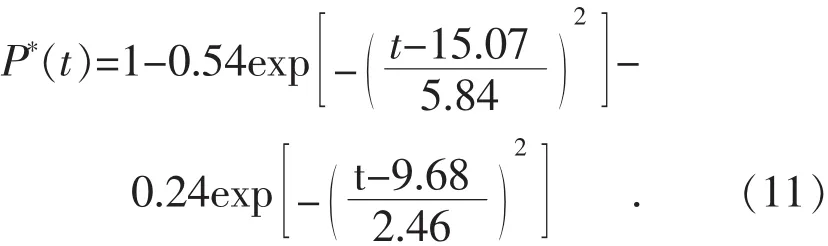
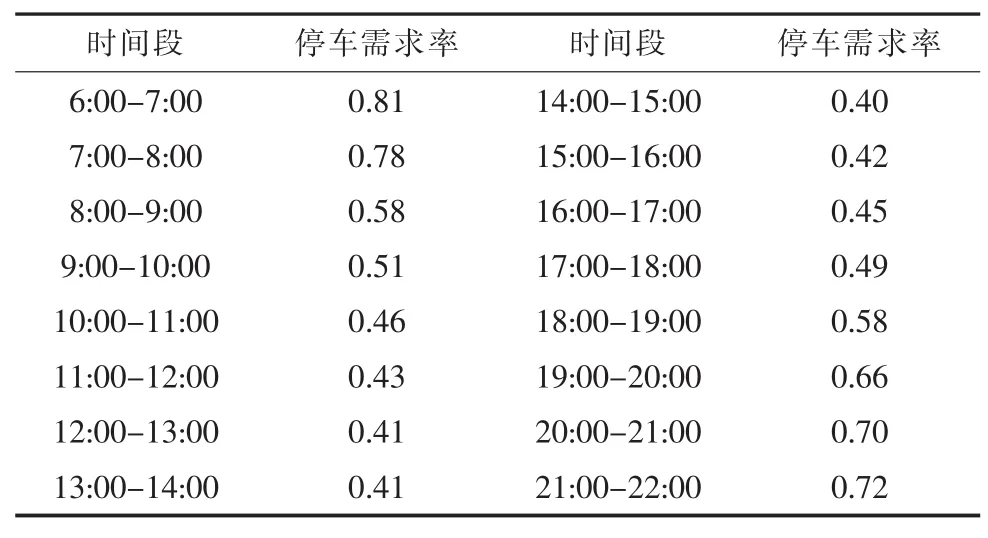
表1 典型居民区的停车需求率
对某地区工商业区的停车需求调研结果如表2所示。
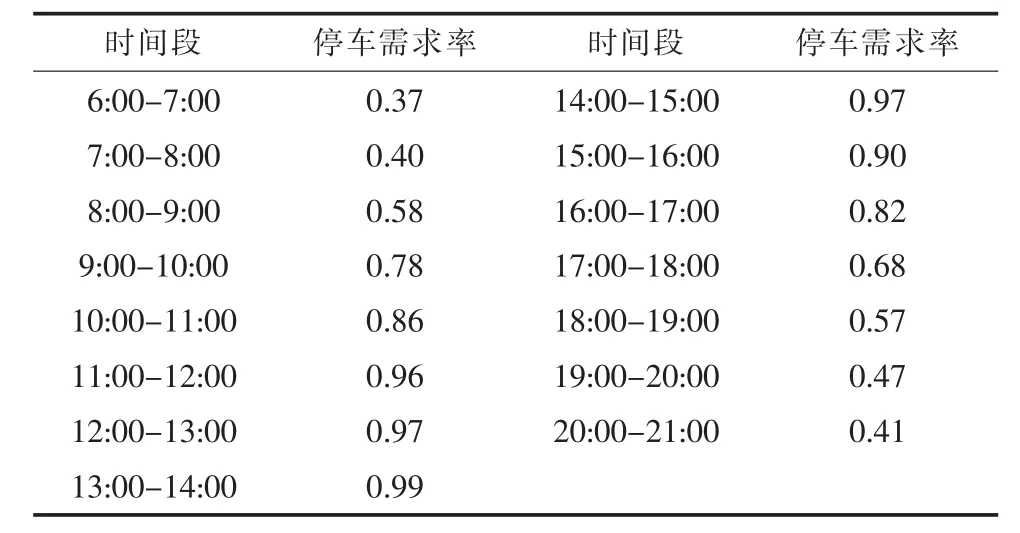
表2 典型工商业区的停车需求率
对表2中的数据进行拟合,得到典型工商业区t时刻的停车需求率函数,如式(13)所示。
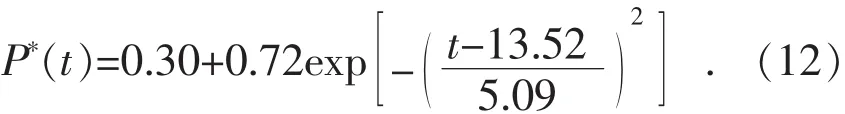
3.2 电动汽车负荷分布的时间特性
停车生成率是指某个区域单位建设用地所产生的最大停车需求,可以通过调研得到该结果。根据停车生成率和停车需求率,可以得到第i区t时刻的停车需求Pi(t),如式(15)所示。

式中:ri为第i区的停车生成率;Si为第i区的建设用地;为第i区t时刻的停车需求率;ki为考虑该区域受该市人口密度、发展趋势、经济状况等因素后的停车生成率修正系数。
假设某市共有n个区域,则该市t时刻的停车总需求P(t)如式(14)所示。
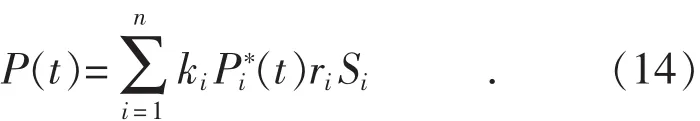
3.3 电动汽车最大负荷区域的确定
由3.2节已知t时刻i区域的停车需求量,则该区域当天总的停车需求量为:
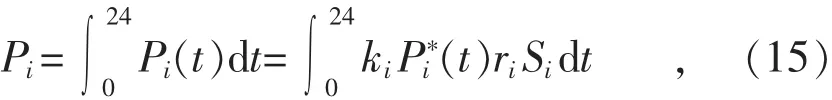
因此,该市的最大负荷区域可表示为:Pmax= max{P1,P2,…,Pi,…,Pn}。
为便于计算,并且更加清楚地看到各时段各区域的停车需求量,令ai,j=Pi(j),其中j=1,2,…,24,则各时段各区域的停车需求量可用矩阵表示为式(16):

4 实例验证
为了验证文中所提基于电动汽车时空分布特性的充电桩规划方法的有效性,利用上述方法,首先根据国外某个小区域的2个典型小区(工业区和居民小区)2000—2015年的电动汽车日最大充电量数据进行仿真计算,确定最佳的平滑系数,并预测后续5年电动汽车典型日最大充电量,仿真结果如图2、图3所示。采用如式(17)所示平均绝对百分误差作为判断此预测方法优劣的依据,误差如表3所示。
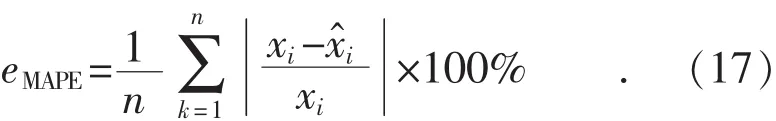
从图2、图3和表3可以看出,利用自适应动态三次指数平滑法对2005—2015年期间日最大充电量预测的误差很小,效果很好,可以满足电动汽车后续年日最大充电量预测的需要。另外,从图中不难看出,2010年前后,电动汽车的充电量需求开始急剧增加,这与当前的社会发展和技术发展有很大关系,尤其是与各国政府对电动汽车的支持力度大大增加密不可分。
根据工业区和居民小区的电动汽车未来充电量需求预测结果,结合电动汽车的时空分布特性,对2020年2个小区的典型日电动汽车充电功率进行仿真计算,典型日每小时预计的充电功率如图4、图5所示。由于白天很多居民都要上班,所以居民小区白天时段的电动汽车充电功率较小,工业区的电动汽车充电负荷大;而下班后居民小区的电动汽车逐渐回家,需要充电,负荷慢慢变大,工业区由于电动汽车量减少,故充电负荷也随之减少。图4和图5的结果恰好反映了电动汽车充电负荷的时空特点,与实际相吻合。
根据预测出来的充电量需求和典型日充电功率分布情况,建议工业区增加充电桩的数量,最好能达到3 500 kW的供电能力,满足工业区电动汽车最大负荷的需求。居民小区也相应增加充电桩数量,最好能达到3 000 kW的供电能力,满足居民小区电动汽车的充电需求。以一般中小型电动汽车为例,单台充满需用电18 kWh、耗时6 h。由于居民工作地点不同,虽然大部分在此工业区,但下班时间不一样,回家时间更是因人而异,因此居民小区的充电时间相对分散,时间跨度大,所以其充电量需求大,但是最大的充电功率相对工业区较小。对于较大的一个区域或者地区,可以分成若干个小区,用类似的方法进行充电桩规划研究。
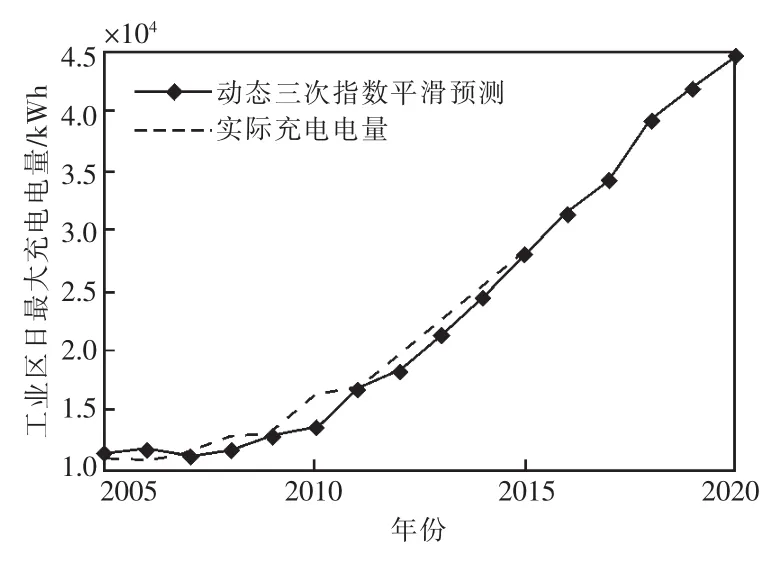
图2 工业区电动汽车日最大充电量
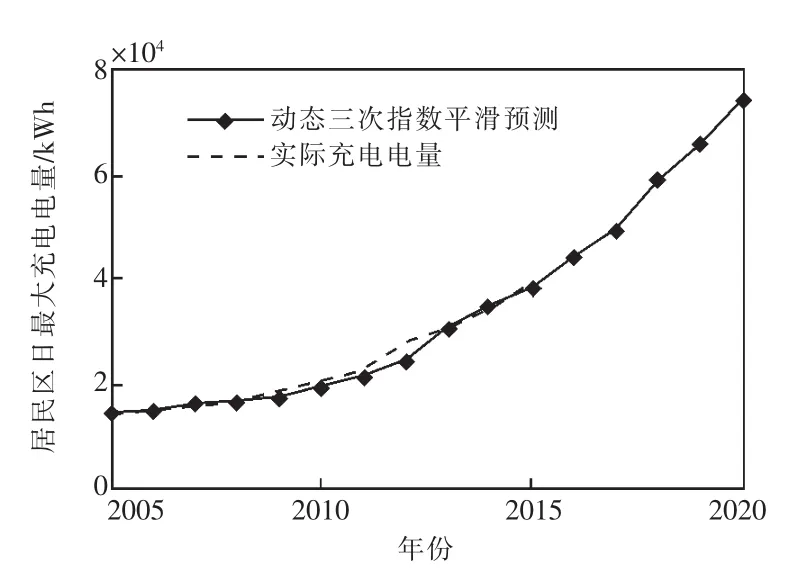
图3 居民小区电动汽车日最大充电量

表3 2个小区的电动汽车充电量预测误差
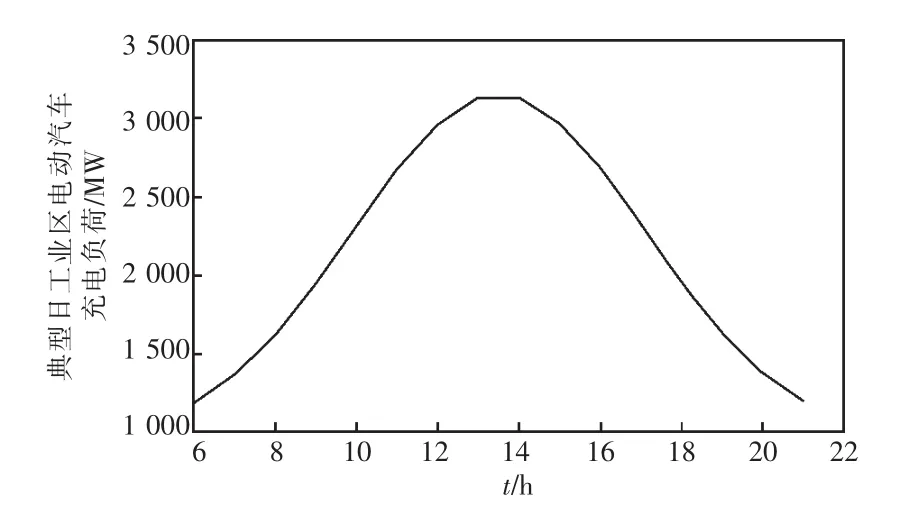
图4 典型日工业区电动汽车充电负荷
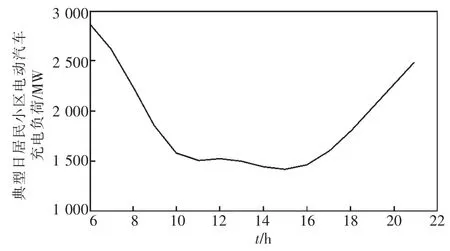
图5 典型日居民小区电动汽车充电负荷
5 结语
利用自适应动态三次指数平滑法对区域电动汽车的年典型(最大)日充电量进行了需求预测,并根据预测结果,结合工业区和居民小区人们的工作、生活习惯分析了电动汽车的时空分布特性,在此基础上对预测年典型日的电动汽车负荷进行了仿真分析,给出了预测年2个小区的充电桩需求建议。仿真实例证明:上述预测方法切实可行,可满足电动汽车充电量预测的要求,预测精度较高;电动汽车预测年的典型日充电功率也符合实际情况,工业区和居民小区早晚时间段的充电负荷时空分布特性明显;对充电桩的规划建议也切合仿真实例,有一定的参考意义。通过对电动汽车负荷预测方法的研究及充电桩的规划,不仅可以更好地服务于电网规划,还可以为今后全球能源互联网的建设提供相应的技术支持。
[1]陈楚月.电动汽车充换电需求分析与预测[D].北京:北京交通大学,2015.
[2]李佩珩,易翔翔,侯福深.国外电动汽车发展现状及对我国电动汽车发展的启示[J].北京工业大学学报,2004,30(1)∶49-54.
[3]李如琦,苏浩益.基于排队论的电动汽车充电设施优化配置[J].电力系统自动化,2011,35(14)∶58-61.
[4]马琳琳,杨军,付聪,等.电动汽车充放电对电网影响研究综述[J].电力系统保护与控制,2013,41(3)∶140-148.
[5]王国权,王森,刘华勇,等.基于自适应的动态三次指数平滑法的风电场风速预测[J].电力系统保护与控制,2014,42(15)∶117-122.
[6]杨秀媛,肖洋,陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报,2005,25(11)∶1-5.
[7]王耀武.电动汽车负荷预测方法适应性与应用研究[D].北京:北京交通大学,2015.
[8]罗卓伟,胡泽春,宋永华,等.电动汽车充电负荷计算方法[J].电力系统自动化,2011,35(14)∶36-42.
[9]田立亭,史双龙,贾卓,等.电动汽车充电需求的统计学建模方法[J].电网技术,2010,34(11)∶126-130.
[10]贺鹏,徐虹,艾欣,等.电动汽车日充电负荷需求模型比较分析[J].电力学报,2012,27(5)∶451-454.
[11]杨冰,王丽芳,廖承林.大规模电动汽车充电需求及影响因素[J].电工技术学报,2013(2)∶22-27.
(本文编辑:方明霞)
Charging Load Forecasting of Electric Vehicle Based on the Characteristics of Spatiotemporal Distribution
WANG Sen,FENG Yaoxuan,DENG Wenxiong,ZHOU Gang,SHENG Pengfei
(State Grid Jiaxing Power Supply Company,Jiaxing Zhejiang 314000,China)
With the rapid development and application of electric vehicles,the accurate charging load forecasting of electric vehicles is becoming a research focus.In order to handle the grid load balance with the electric vehicles expansion,this paper proposes a self-adaptive and dynamic forecasting method based on electric vehicle features of spatiotemporal distribution.The forecasting model improves the traditional cubic exponential smoothing model,and the ideal smoothing factor is changed in time by the principle of minimum absolute value error;then electric vehicle charging quantity and charging load forecasting from different areas on typical day can be done with the new method.Load distribution of electric vehicles in an industrial area and residential quarter is simulated,and the result shows that the method can reduce errors and its suggestions on charging poles are practical and feasible.The simulation results show that the proposed method is feasible.
electric vehicle;load balance;features of spatiotemporal;self-adaptive;load forecasting
项目:国网浙江省电力公司群众性科技创新项目(5211JX1500KM)
TM715+.1
B
1007-1881(2016)12-0015-06
2016-10-17
王 森(1988),男,工程师,研究方向为配电网规划、电力系统及其自动化。
