虹吸管内气团流流型时流动压降计算
2016-03-26王梦婷谭义海
李 琳,王梦婷,谭义海
(1.新疆农业大学水利与土木工程学院,乌鲁木齐 830052 2. 新疆新能源新风投资开发有限公司,乌鲁木齐 830000)
国内学者对正压管道的压降进行了大量的研究,如张西民[1]分析了水平放置的圆管内气水、油气摩擦阻力压降的特性;韩炜[2]研究了气液两相流的压降计算方法,并建立了相关模型对压降的变化规律进行了分析;许晶禹[3]对牛顿及非牛顿流体的气液流动进行了研究,并分别研究了两种不同流体的压降的变化规律,且建立了精度较高的预测模型。汤勃[4]依据稳定一维流动的基本方程推导出了水平圆管压降的计算式,并总结了含气量与压降的关系。但是前人主要针对正压管道内的气液两相流动压降开展研究。在坎儿井式地下水库中,水平管段距离长、正虹吸式输水管道是其重要组成部分,管道在负压下运行,设计人员按照有压管流流量公式计算其过流能力,用达西公式计算管道压降。但是李琳[5]、许史[6,7]等在新疆台兰河某地下水库长距离虹吸管道水力学模型试验中发现即使在安装高度小于7 m时,虹吸管内已然是气液两相流,随安装高度增大管内水流伪空化现象加剧,流动介质由单一液相流逐渐转变为气泡流、过渡流和气团流流型(如图1所示)。气泡流是指由于压强较低,自然水中少量肉眼看不见的极微小且不溶解于水的气核,由于气核内部压强大于外部压强而膨胀析出,以分散的球形小气泡的形式分布在管道上部,随水流连续向下游运动。当管内压强进一步降低时,大量气泡析出并聚合形成大气泡,大气泡在缓慢运动的过程中逐渐聚合成形成气囊,管内呈现气团流。介于气泡流和气团流之间的流型即为过渡流。许史[6,7]、王梦婷[8]分别对常规有压管流流量计算公式应用于虹吸管气液两相流实际过流能力计算进行了修正。同时,已有研究表明当水平输水段较长的虹吸管内由于伪空化现象而形成的气泡流压降特性与液相满流时的压降特性不同,不能直接采用达西公式计算流动压降,推导出了专门适用于气泡流流型时的管道压降计算公式。然而,过渡流和气团流流型与气泡流流型差异明显,截面含气率、气泡形状、气囊的长度明显不同于气泡流,影响其管路压降的因素理应不同于气泡流,不能采用同一公式进行计算。因此,为了探讨不同真空度、气团流流型下虹吸管道流动压降的影响因素及其区别于液相有压满流的气液两相流管道压降计算方法,笔者针对不同真空度非驼峰式正虹吸管道气团流流型进行了系列试验。根据试验结果,分析实际过流面积减小对气团流流动压降的影响,推导出适用于气团流流型下伪空化现象明显、安装高度不大于8 m的水平管段较长的虹吸管水平管段压降计算公式。由于本系列试验旨在根据试验结果探讨虹吸管水平管段气液两相流动压降计算方法,故不涉及原型和模型的比尺问题。
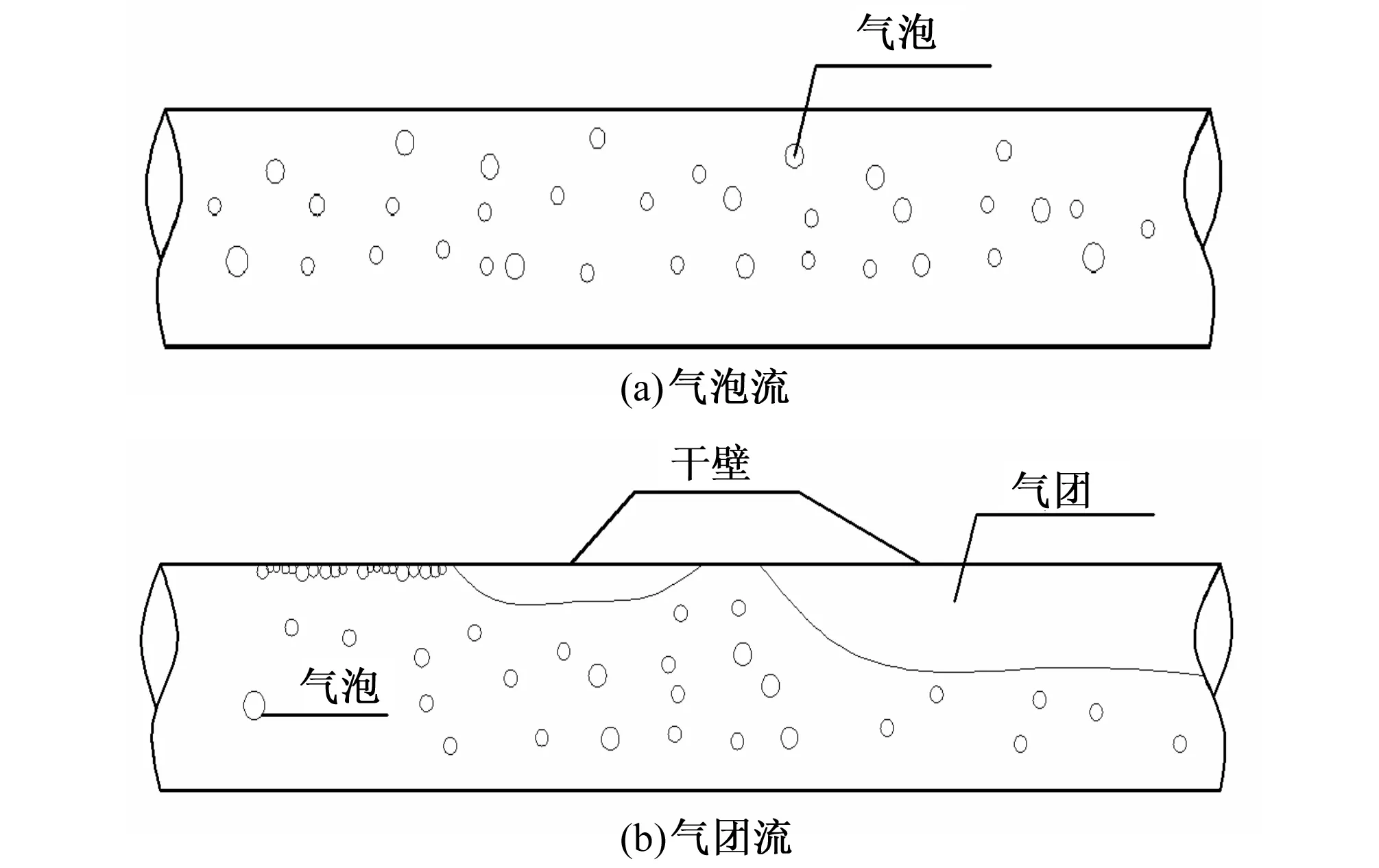
图1 流型示意图Fig.1 The schematic diagram of flow pattern
1 试验方案
1.1 试验装置
试验装置如图2所示。试验装置由上游进口溢流堰、虹吸管路、下游出口堰组成。在上、下游水箱中各布置一溢流堰,上游溢流堰为活动式,用于恒定水位和调节上下游水位差,保证每组试验中管路水头不变。虹吸管路由有机玻璃制作而成,管长为17.7 m,管径为2 cm,整个试验中管道相互连接处均为密封状态。水平管路上下游各安装一个压力传感器(KYB11G/A)与DJ800数据采集系统进行量测,测量精度为0.25%,试验前对空管时的压降进行了标定(空管时的相对压降为0 kPa)。虹吸管道流量用20°开口三角形薄壁堰量测;在水平管段从上游至下游依次布置5个环形掺气电极,截面含气率用电导率仪(DDLY-2005)与DJ800数据采集系统进行量测,电导率仪的误差小于0.5%,在每次测量前,均进行一次满度标定(空管时掺气浓度仪的显示值为100)。试验采用充水排气法,待管路充满水后,管内气体排出,在一定的上下游水位差下管道形成自然虹吸。虹吸形成后进行流量、压降及含气率的量测。通过环形电极量测管段典型断面的截面含气率,截面含气率与管道断面积的乘积即为气体所占面积,管道断面积与气体面积之差为实测过流断面积AS。
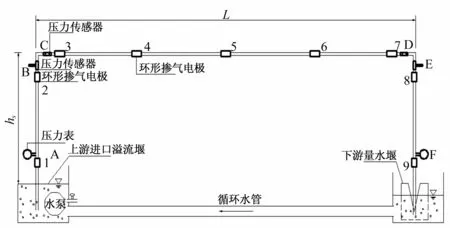
图2 试验布置示意图Fig.2 The schematic diagram of test arrangement
1.2 试验工况
试验分别在安装高度hs=1、2、3、4、5、6、7、8 m,上下游水位差H从7.0 cm增加至68.0 cm,共13个水位差下展开试验。在确定hs之后,调节不同H值,通过记录、拍照或录制视频等方法观察虹吸管内的气液两相流动现象,并对虹吸管内流量、压降及截面含气率的大小进行量测。
2 结果及分析
2.1 虹吸管内气团流压降特性及影响因素分析
试验量测了hs=1~8 m各工况下水平管路压降值。试验结果表明,在相同安装高度下,随着H的增大,管道过流量增加,管内流速增大,气泡流和气团流流型时水平管段ΔP随之增大。另外,由达西公式可知,有压管流压降与虹吸管安装高度无关。但是试验结果(见图3、4)表明,虹吸管道压降随着管安装高度的增大而减小。从图3可以看出,hs=2 m的气泡流流型时管道压降值与单一液相满流(hs=1 m)时的压降值基本相同,安装高度的增大对压降值基本无影响。而气团流流型[图3(b)]时压降值均小于单一液相满流时压降值,特别是管道水头较小时,安装高度越大,压降值越小,随水头增大,安装高度对压降值的影响越来越小。H一定时,不同hs时的ΔP也不相同。图4为H一定时,hs与ΔP的关系图。由图4可知,H一定,随着hs的增大,ΔP逐渐减小。如H=7 cm时,hs=1、2、4和7 m时的ΔP分别为1.21、1.13、0.91和0.77 kPa,与液相满流相比压降减小率依次为0、6.6%、24.8%、36.3%。而当管道水头H增加至68 cm时,hs=1、2、4和7 m时的ΔP分别为5.69、5.61、5.48和5.38 kPa,与液相满流相比压降减小率依次为0、1.4%、3.7%、5.4%。显然,随着管道水头的增大,管道压降值愈接近单一液相压降值,这是因为试验中H>68 cm后,管内流型由气团流转变为气泡流。
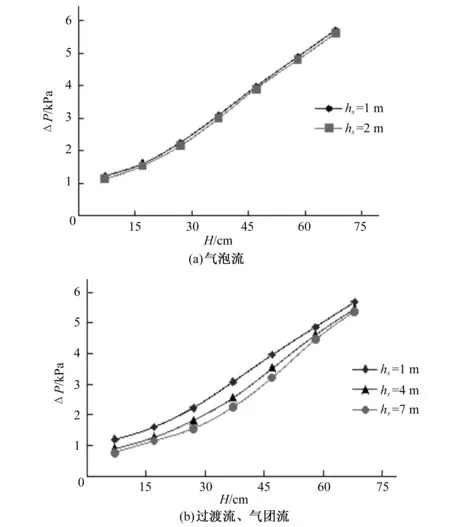
图3 hs一定时水位差与压降的关系图Fig.3 Under the same installation height, the relation graph of water head and pressure drop
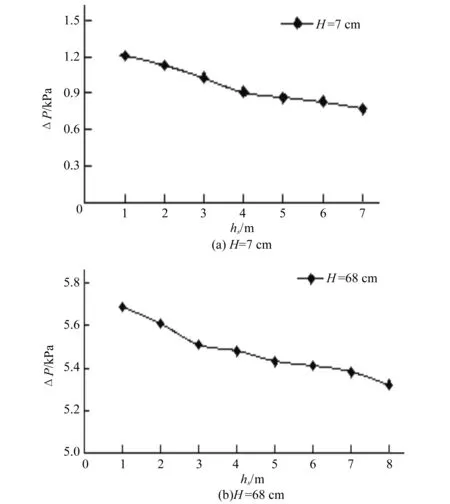
图4 不同水位差下安装高度与压降的关系图Fig.4 Under different water head, the relation graph of installation height and pressure drop
为了衡量虹吸管气液两相流与液相满流相比时的压降减小率ΔP′。将各个水位差下虹吸管内单一液相满流时(hs=1 m)的压降值作为理论值ΔPL,实测虹吸管气团流流型下不同水位差时的管道压降ΔPS作为实测值,具体见式(1)。
ΔP′=(ΔPL-ΔPS)/ΔPL×100%
(1)
将管道水头H、安装高度hs与压降减小率ΔP′的关系绘制于图5中。管道H相同时,hs越大,ΔP′也越大,即压降理论值与实测值之间的差值随着hs的增大而增大。H越大,各安装高度相应的ΔP′越小,即压降理论值与实测值的差值随着H的增大而减小。如当H=7 cm时,hs由2 m增至7 m的过程中,相应的ΔP′由10.7%增大至36.4%;当H=37 cm时,hs由2 m增至7 m过程中,相应的ΔP′由4.2%增大至26.6%;当H=68 cm时,hs由2 m增至8 m过程中,相应的ΔP′由2.3%增大至6.5%。可见,当H=58 cm、68 cm时,压降理论值与实测值愈接近,且其差值与hs的相关性越小。
由式(2)可知,在管道长度l、管径d、水位差H以及管道的布置形式一定时,影响虹吸管道压降的因素为流速和沿程阻力系数λ。显然,管道水头相同、安装高度不同使得管内真空度不同,水源中肉眼看不见的小气核析出数量因压强降低程度不同而不同,使管道截面含气率不同。因此,管道实际过流断面面积不同,相同水头时管内流速大小不同。假定气团流流型下气体存在对虹吸管道λ影响很小,可忽略不计,即认为相同水位差、不同安装高度或者相同安装高度、不同水位差时虹吸管的λ与含气率无关,压降变化仅是由于流速v变化引起的,具体见式(3),式中vL表示圆管满流时(hs=1 m)的流速理论值,vs表示相应于实测流量的流速实测值,vs=Qs/As。为了检验此假定的合理性,将H为7~68 cm,hs为2~7 m时对应气泡流流型时的ΔP′与Δv″关系绘制于图6中。
(2)
ΔP′=(ΔPL-ΔPS)/ΔPL=(v2L-v2s)/v2L=Δv″
(3)
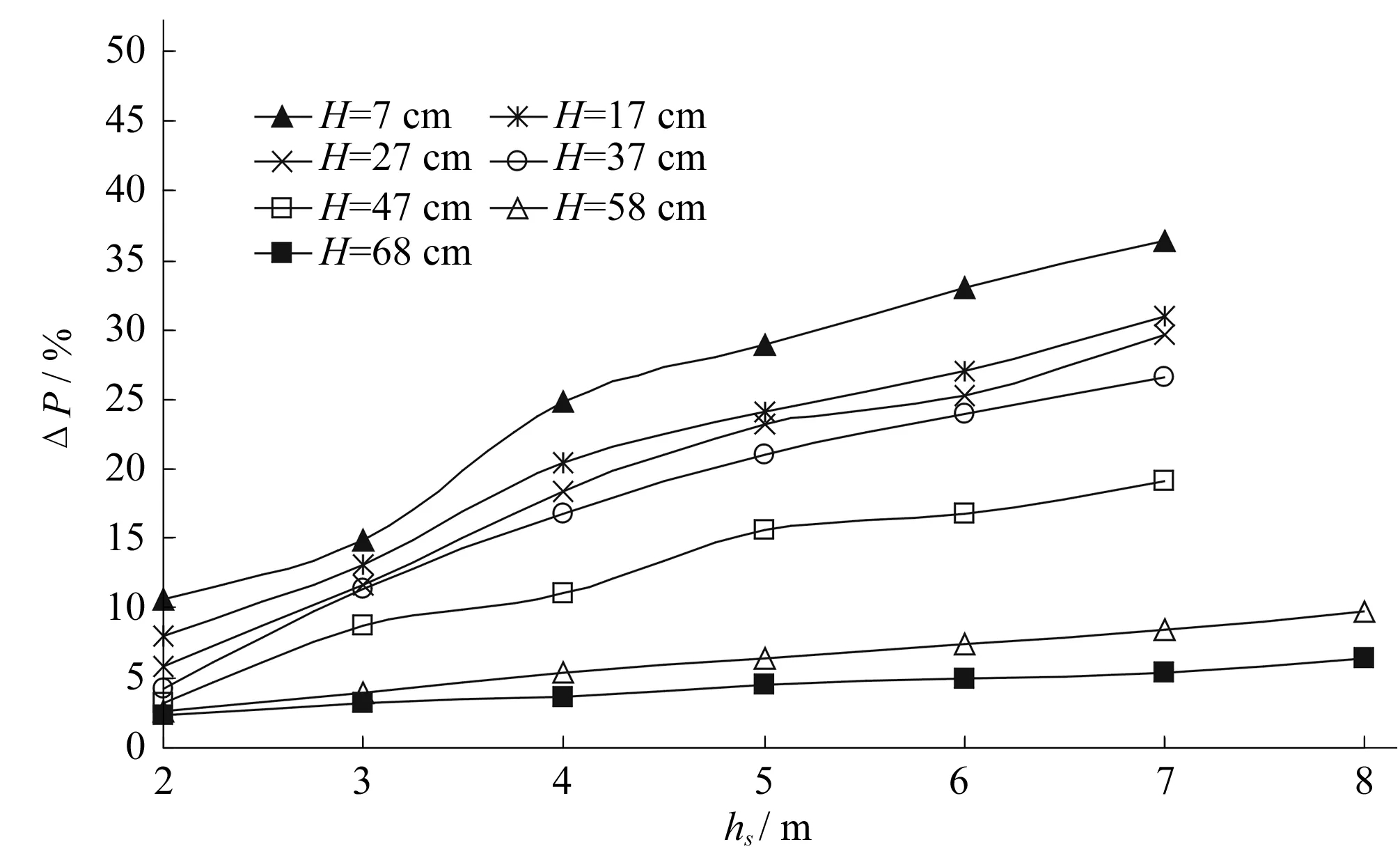
图5 不同安装高度hs与ΔP′关系曲线图Fig.5 Under different installation heights,the relationship between hs and ΔP′
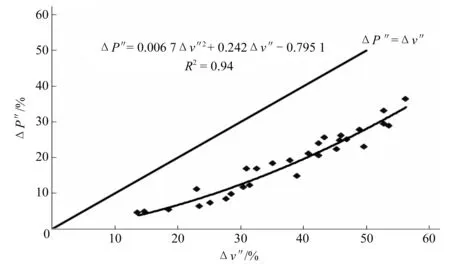
图6 气团流时ΔP″与Δv″的关系图Fig.6 Under air mass flow, the relationship between ΔP″ and Δv″
从图6可以看出,ΔP″≠Δv″。由此说明,前文中提出的“气体存在对虹吸管道沿程阻力系数影响很小,可忽略不计,不同安装高度时虹吸管的压降减小仅是由过水断面积A引起流速v变化而引起的”的假定对于气团流而言不合理。对于气团流而言,过流面积减小、流速减小不是导致流动压降减小的唯一因素,除了考虑流速减小对压降的影响外,还应考虑含气率大小引起的λ变化对压降的影响,即气团流流型时沿程阻力系数λ除了与雷诺数、相对粗糙度有关外,还应与截面含气率α有关。
2.2 公式推导及验证
假定管道水头相同时,气团流流型下的虹吸管流动压降实测值与忽略气体存在按单一液相有压流动计算的压降理论值之间存在函数φxbf,即:
ΔPL=ΔPSφxbf
(4)
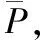
(5)
φxbf=f(Cpmin,Re,α,ρa/ρw)
(6)
采用hs=3、4 m的试验数据来应用数值分析法推导φxbf与各无量纲数之间的关系式。在试验过程中,温度和压强基本保持不变,因此空气与水的密度保持不变,视ρa/ρw为常数,令K=(ρa/ρw)·Re,则通过数值拟合得到φxbf与K的关系如图7所示。
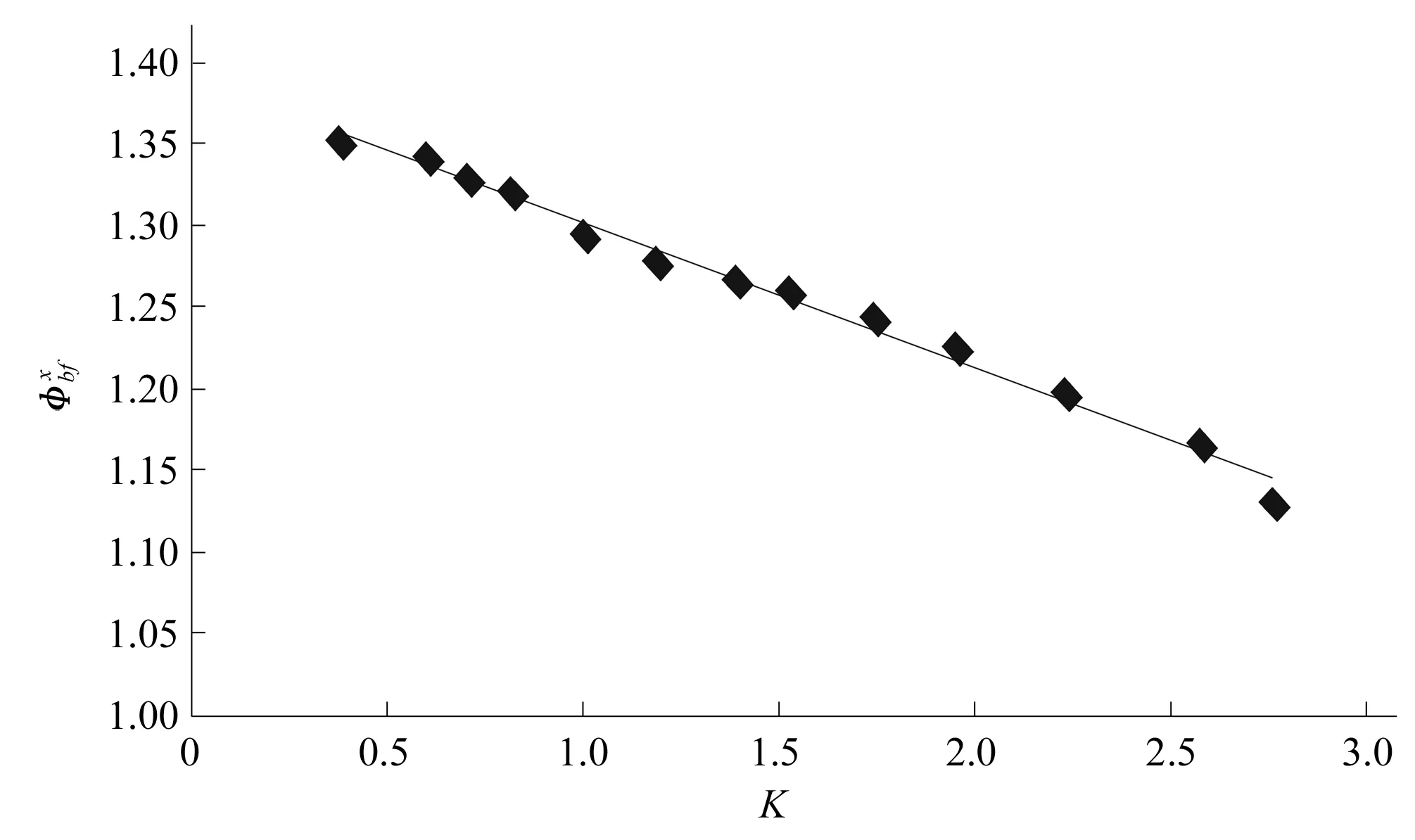
图7 φxbf与K的关系Fig.7 The relationship between φxbf and K
由图7可知,φxbf∝(-0.088K+1.391),假定:
Z=φxbf/(-0.088K+1.391)
(7)
令B=(CP)minα
(8)
则通过数值拟合得到Z与B的关系如图8所示。由图8可得,Z与B的关系为:
Z=(0.059 2B2-0.417B+0.147)
(9)
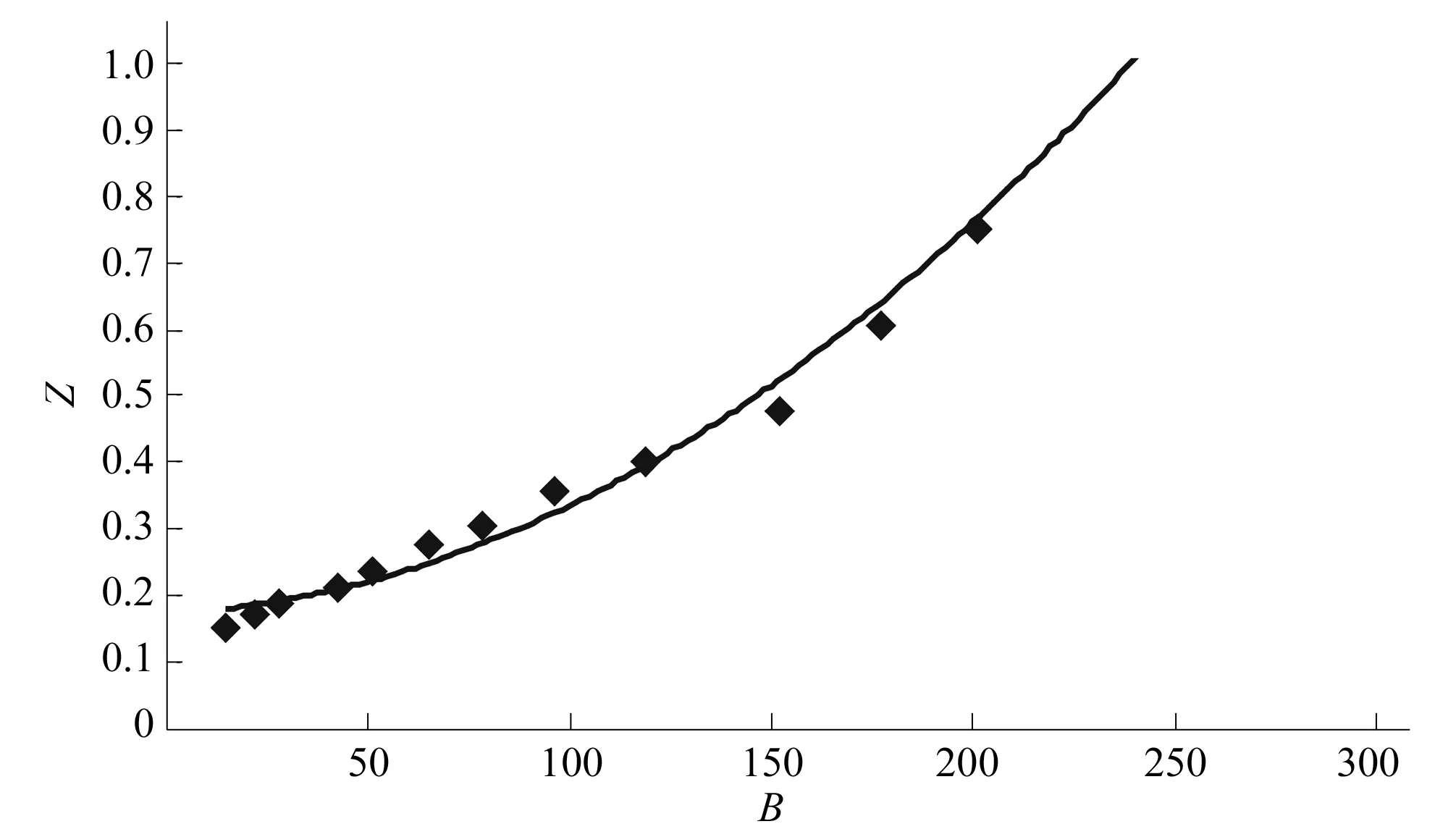
图8 Z与B的关系Fig.8 The relationship between Z and B
联立式(7)、(8)和(9),可得:
φxbf=[(-0.088K+1.391) (0.059 2B2-
0.417B+0.147)]
(10)
将式(10)代入式(4)中,可得:
ΔPS=ΔPL/φxbf
(11)
在应用式(11)计算虹吸管内气团流压降时,可先按照单一液相有压流压降公式计算ΔPL,再根据式(10)计算φxbf,将ΔPL和φxbf代入式(11)中,即可得到气团流时管路压降值。采用hs=5、6、7、8 m时气团流流型时的数据代入式(11)计算压降值,将计算值与实测值进行对比,结果如图9所示。从图9中可以看出,二者的相对误差都控制在±7%以内,而按照单一液相有压满流计算时最大误差可达40%(见2.1节),显然公式(11)误差相对较小。
3 结 语
文章通过系列试验获得了不同工况下气团流流型时虹吸管水平管段压降、过流量和含气率的大小,根据试验结果,分析影响气团流流动压降的影响因素。结果表明气团流流型时气体存在对虹吸管道沿程阻力系数影响较大,不可忽略。不同安装高度时流速减小不是导致虹吸管流动压降减小的唯一因素,除了考虑流速减小对管道压降的影响外,还应考虑含气率大小引起的μ0或λ变化对压降的影响,此时,沿程阻力系数λ除了与雷诺数、相对粗糙度有关外,还应与截面含气率有关。推导出适用于气团流流型下伪空化现象明显、安装高度不大于8 m的水平管段较长的虹吸管水平管段压降计算公式,经检验,公式计算误差不超过±7%,可用于伪空化现象较明显、安装高度不大于8 m的非驼峰式虹吸管内流型为气团流时的压降计算,为工程设计和运行提供参考。
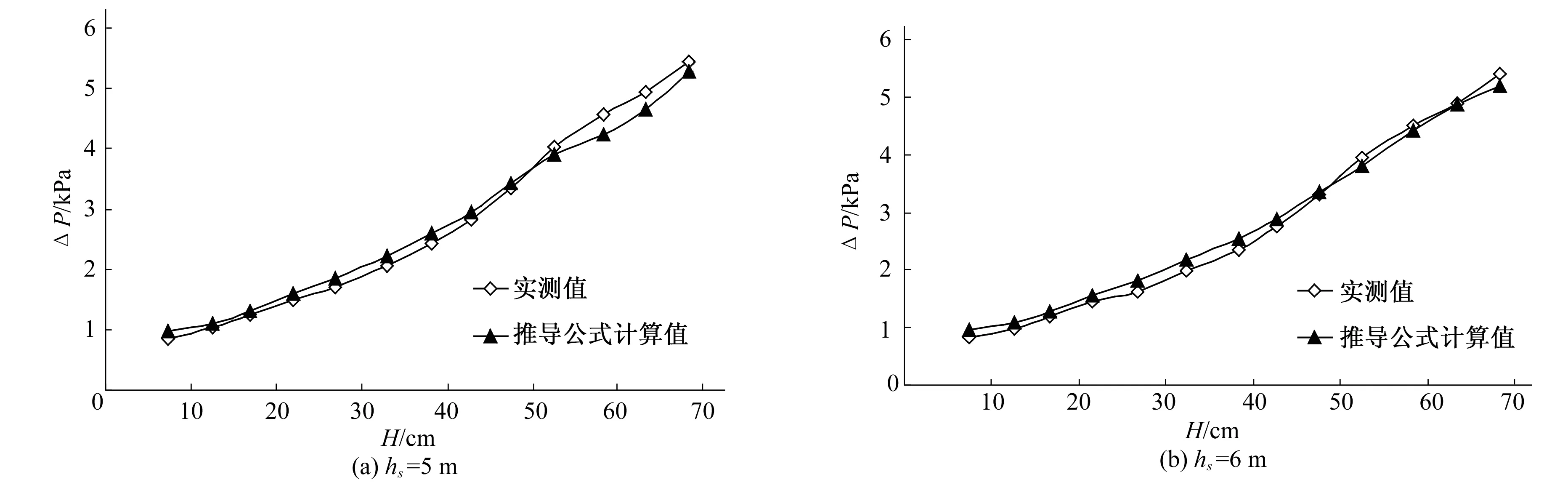
图9 水平管段内气团流时压降实测值与计算值对比图Fig.9 The contrast diagram of measured value and calculated value of pressure drop when air mass flow is in horizontal pipe
□
[1] 姜俊红,戴红霞.驼峰后带长直管虹吸式出水流道的水力特性试验研究[J],中国农村水利水电,2008,(8):130-132.
[2] 施俊跃,陈革强,卢健国.水库虹吸管的运用特性[J].水利技术监督,2008,(3):41-43.
[3] 王卫平.虹吸管在水库放水涵管改造中的应用[J],节水灌溉,2008,(1):51-53.
[4] 李 娟.长距离倒虹吸水流特性的三维数值模拟[D]. 乌鲁木齐:新疆农业大学,2013.
[5] 李 琳,邱秀云,许 史,等.长距离虹吸管道输水水力学模型试验研究[J].南水北调与水利科技, 2010,8(3): 106-109.
[6] 许 史,李 琳,邱秀云,等.长距离虹吸管输水试验研究初探[J].中国农村水利水电,2010,(3): 70-72.
[7] 许 史.长距离虹吸管输水试验研究[D]. 乌鲁木齐:新疆农业大学,2010.
[8] 王梦婷,李 琳,谭义海,等.正虹吸管道水力特性实验研究[J].水电能源科学,2014,(12):87-90.
