运用差异化教学发展学生思维

崔小兵

建构主义理论认为：每一个学生都是独特的，具有独特的思维方式。新课改提出，要以学生为主体，尊重学生的个性思维，构建和谐的生态系统。在这个生态系统中，教师处于主导地位，一方面要尊重学生的个体差异，另一方面要张扬学生个性，提升学生的个性思维，构建差异化的生态课堂。那么，如何实施差异化教学策略呢？笔者根据多年教学实践所得，认为可以从以下四个方面着手：

一、多元引导尊重差异，凸显数学思维

学生之间存在着个体差异，教师要正视并尊重和发现这种差异，并善于运用学生之间的这种差异，实施多元引导，带领学生自主探究，展开多元思考，通过对比辨析让不同层次的学生在课堂上获得思维的发展。

例如，在教学完“圆柱体和圆锥体”这一内容之后，根据教材中的习题（如图），笔者让学生展开多元思考：目测一下，图中的圆锥体和①②③④哪个圆柱体体积绝对不相等？有学生认为①号圆柱体太大，也有学生认为④号圆柱体太小，因而和圆锥体的体积绝对不相等。

判断下面的圆锥与哪个圆柱的体积相等（单位：cm）。

教师继续展开引导：你认为①号圆柱体和圆锥体之间有什么关系？有的学生根据题目中给出的数据，认为圆柱体①和圆锥体是等底等高，因而体积是圆锥体的3倍。圆锥体体积和哪个圆柱体体积疑似相等？为什么？有的学生认为圆锥体体积和圆柱体②号相等，也有学生认为圆锥体体积和③号圆柱体体积相等。那么，到底哪个一定相等呢？此时笔者尊重学生的个体差异，引导学生展开探究，学生根据等底等高这个基本要素，认为底面直径相等，高是圆锥体体积的三分之一，因此③号圆柱体体积一定和圆锥体体积相等。

此时，学生的思维被激活，对圆锥与②号圆柱体的关系展开研究，认为直径之比为9∶3=3∶1，因而底面积之比为9∶1，再加上高相等，因而圆锥体和②号圆柱体的体积之比为3∶1。

通过这样的多元引导，教师以学生差异为主导，引领学生自主探究，层层深入，在不同观点的碰撞下营造出一个和谐的生态课堂，使每一个学生都从不同的层面获得了能力提升。

二、对比辨析发现差异，提升思维张力

对于学生来说，由于生活环境、个人性格的不同，必然会造成思维的差异，导致问题解决的策略也迥然有异。教师要关注这些个性差异，立足差异，重点将这种差异彰显出来，相互补充完善，激发学生的思考动力。

以上教学环节，教师将重心放在学生的思维差异上，立足思考，并以此为契机展开引导，激发学生的探究动力，让数学课堂多姿多彩，充满了思维张力。

三、加强合作运用差异，建构数学概念

在小学数学生态课堂中，教师要运用学生间的思维差异，有意识地建立不同思维层次间的广泛联系，建构问题化的问题情境，引导学生循序渐进，让不同层次的学生都能够通过差异化互助合作，自主完成对知识的探究和建构。

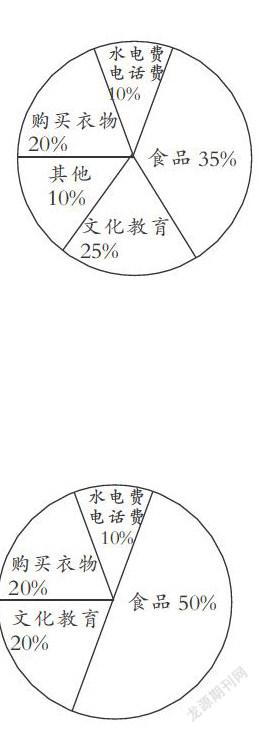
例如，在教学完“百分数”这一数学知识之后，教师根据教材内容，设计了这样一道练习题：出示情境图，设计6个问题逐步丰富情境图：

问题一：这是小明家8月份的支出情况，（先不出示数据）从图中你知道了什么？你能估计各种支出大约占总支出的百分之几吗？

问题二：食品支出最多，想要知道食品支出多少元，需要知道什么？

问题三：如果总支出为2 500元，小明家食品支出了多少元？

问题四：如果不知道总支出，只知道水电和电话费的支出是240元，你能知道购买衣服支出了多少元吗？

问题五：出示小芳家8月份的支出，你认为哪家食品支出多？

问题六：从两幅图中食品支出所占百分数，你能想到什么？

针对问题四，有学生认为可以先求出总支出，240÷10%=2 400元，然后根据购买衣服的比例求出支出的钱数：2 400×20%=480元。但也有学生认为，根据图中所示，购买衣物支出所占百分数是水电电话费支出的2倍，因而只需要：240×2=480元。

通过这6个问题，让学生规避了思维定式，按照自己的不同理解寻找解决办法，建构了生态课堂下差异化教学的自主思维模式。

以上教学设计，教师采用6个问题的设置，给不同的学生提供了独立的思考机会，拓宽了学生的解题思路，同时激发了学生的个性思维，使数学课堂在差异共融中实现了有效教学。

四、超越差异激活经验，凸显数学本质

学生个体在数学思维上的不同，是一种宝贵的教学资源，教师要重视这种差异，并超越差异，通过个性化的问题表征，激活学生头脑中相关的知识经验，彰显思维的个性表征，凸显数学本质。

以上教学环节，通过对学生的差异引导，教师打通学生这两种不同方法的“气脉”，帮助学生从整体上把握这两种方法，更有助于学生深刻地理解这两种方法，从而深入理解了数学本质，提升了学生的思维个性表征能力。

总之，差异是一种客观存在的教学资源，教师要善用这一资源，实现数学课堂的生态和谐，提升课堂教学的实效性和有效性。