“集合与分类”核心经验概说

黄瑾

生活中充满了可供儿童感知和形成集合与分类经验的各种机会：把自己的玩具柜清理一下，把玩具分类归放整齐；把娃娃家厨房里的餐具摆放好，把点心店里的点心和标牌对应起来；把散步时搜集起来的落叶加以分类；给音乐角的小乐器分分类，等等。这些自然发生的活动可以引发儿童关于集合与分类的学习。儿童在这类活动过程中都会涉及一个最基本的数学认知核心经验——集合与分类。

一、什么是集合与分类

在数学中，某种具有相同属性事物的全体称为集合。在日常生活中，人们经常会把同类事物归为一体，如把梨子、苹果、橙子归在一起，这就是水果的集合；把汽车、火车、飞机、轮船归在一起，这就是交通工具的集合。集合的归并是以对象所具有的共同属性为条件的。实际上，为了学习某些事物的名称，幼儿常常会在脑海里创造一些集合，比如关于“狗”的集合，就包括自己家的狗、邻居的狗、路边的狗，他们会把这三种不同地方的狗在头脑中汇合起来创造出一个有关“狗”的集合概念。

集合是幼儿形成数概念系统的基础。用数字描述一个集合有“多少”是非常重要的，如有1个、7个或者100个，等等，它们是这个集合的元素数量。在我们要指出“这里有多少个苹果”之前，必须先知道哪些是苹果，哪些不是苹果。一旦形成了关于苹果的集合概念，就会很自然地把它和梨子、橙子等区分开来，再数它们有多少个。数数是以集合为基础的，认识集合的属性对幼儿的数学学习具有重要的影响。

分类是指将一组事物按照特定的标准加以区分，并同时进行归类的过程。在很多情况下，儿童都会自然用到分类方法，如将一堆物品分成玩具和文具两类，把不同形状的积木加以区分摆放等。分类和集合是紧密联系在一起的两个概念：分类是对不同集合进行区分的过程、是建立在集合思想的基础之上的。也就是说，集合是分类的基础，对集合先加以区分再进行合并就称为分类。概括地说，集合是对数学概念、数学思想的描述，分类则是对数学能力、数学活动的描述，两者本质上是一体相连的。分类是贯穿儿童思维发展全过程的核心能力，是儿童科学领域学习与发展的重要参考指标。

幼儿在数学学习资源丰富的活动室以及日常生活环境中会碰到很多关于集合、分类（包括匹配）的活动，教师可借机让他们从不同角度对物体进行比较和区别，按照不同的属性对物体进行分类或归类，即探讨如何把一堆物品分成不同的集合等。

二、集合和分类的核心经验要点

要点一：可以根据物体的属性对物体进行匹配、分类，组成不同的集合

相关情景：在建构区，3岁的强强抱来一筐插塑拼板，他抓起一把插塑，大声喊着：“我有好多好多块，我有一百块！我是最多的！”……

在上述活动情景中，我们发现强强对这一筐插塑拼板的关注点集中在数量上，虽然他并没有正确报出准确的数量，但他显然在思考有“多少”，因为他提到了一个很大的数字（一百）以及“最多”。我们可以从插塑拼板中看到，一个（或一群）物体可以具有不同的属性，如颜色、大小、形状、材质、功用、数量等，对属性的关注是儿童对事物（或对象）进行匹配、分类或加以数数的前提。

对于教师来说，应该从这个核心经验要点中领悟到，匹配和分类都涉及对物体属性的把握，但两者还是有差异的：匹配是分类的基础，但分类才是儿童集合概念认知的典型表现。儿童掌握了匹配对应能力不等于掌握了分类能力，对某些数学思维发展相对迟缓的幼儿来说，帮助他们从匹配对应向分类乃至多元化分类发展是非常重要的。如下面一组区角材料设计（见图1、图2），图1的操作材料是要求幼儿将不同颜色的珠子装入相应颜色的罐子里。罐子的颜色对幼儿的操作具有暗示性，因此，它是一个匹配活动；图2的材料是要求幼儿将篮子里的“糖果”分放到挂在墙上的口袋里，教师为幼儿提供了一大一小两个口袋，且两个口袋里已经分别放进了两粒大的糖和两粒小的糖。这样的材料投放给儿童限定的是“糖果”大小的属性，虽然教师要求幼儿把篮子里的“糖果”按大小分别放到对应的口袋里，但这也只是匹配活动而不是分类活动，因为若是分类活动，属性应该由幼儿自己去区分并发现，而不是教师预设的。如果教师提供给幼儿的是两个大小相同且里面没有“糖果”的口袋，要求幼儿将篮子里的“糖果”按大小分类放到两个口袋里，那就是分类活动了。

要点二：同样一组物体可以按照不同的方式进行分类

相关情景：活动室里几个孩子在一起串木珠。小新串的是一串红、黄、蓝颜色相间的珠子，他一边在箩筐里挑选自己需要的珠子，一边看了看边上的桐桐（桐桐所串的是鱼形、星形两两间隔排列的珠子），很快把在箩筐里找到的鱼形珠子递给了桐桐：“这个是你需要的，给你。”……

在上面这个活动情景中，显性反映的是孩子的模式能力，但从中还可以明显看出孩子的分类水平，小新的语言以及行为清晰地表明，他已经具备了根据不同的物体属性分成不同集合的分类能力，即他不仅能够识别出自己模式中的颜色类别，也能在同一堆珠子中发现和找到不同形状的珠子，这体现了他对集合的思考：同一组物体是可以按照不同的方式进行分类的，他意识到了鱼形珠子可以用来作为星形、圆形、方形的参照物，但同样也可以用来作为自己所串的珠子中的“非红黄蓝珠子”。

一般说来，对物体进行分类的方式通常有以下几种：（1）按物体的名称分类，如把书放在一起，把笔放在一起等。（2）按物体的外部特征分类，如按颜色不同，将黄气球放在一起，将蓝气球放在一起；按形状不同，将椭圆形气球放在一起，长条形气球放在一起等。（3）按物体量的差异分类，如把大气球和小气球分别放在两个筐里。（4）按物体的用途分类，如把笔、本子、手工剪刀、铅画纸等归为一类（都是文化用品），把毛巾、牙刷、茶杯等归为一类（都是生活用品）。（5）按物体的材质分类，如将塑料花片、小碗、玩具等归为一类，将积木、木制玩具小厨等归为一类，将布娃娃、衣服、裤子等归为一类。（6）按物体的数量分类，如把数量只有一个的物品放在一起，把数量为两个的物品归在一起等。（7）按事物间的关系分类，如将小兔与萝卜放在一起，将猴子与香蕉放在一起等。

事实上，对于幼儿来说，要理解分类的多样性并不容易，因为这要求他们能够发现一个物体的不同属性。也就是说，在一个集合中，一颗珠子可能会被看作是蝴蝶形的，在某些情况下又可能被看作是粉色的或大的。幼儿理解了这一现象后，就会开始学习相同和不同的概念，开始进行更抽象的思考并尝试解决问题。教师要善于在活动中帮助幼儿去感知事物属性的多样性。如在和幼儿玩“人物分类”的游戏时，教师要求幼儿进行二分法分类（即把人物分为两类，一类有相同的属性，另一类没有）：穿白色衣服的幼儿在一个集合中，没有穿白色衣服的幼儿在另一个集合中。一个男孩犹豫了一会儿，走进了白色衣服集合的呼啦圈里。其他孩子马上告诉他说：“老师说了，这个圈里是穿白色衣服的，你的衣服不是白色的！”但男孩指了指自己身上的白色条纹，坚持说：“我的衣服上有白色，我应该站在这里。”一个穿着红色衬衫，但领子和袖口处为白色的女孩也认为她应该转移到白色集合圈来，而只有一个穿绿色衣服的孩子站在那个非白色衣服的呼啦圈里。此时实际上是一个最佳的教学时机，教师可以这样引导孩子：“我发现你们真的很会思考了。我们再来用两种不同的方法尝试一下。首先，我们按照衣服上有一些白色和完全没有白色来站圈；然后，当我说按纯白衣服和不是纯白衣服来站圈的时候，我们来看看小组会发生什么变化。”这时，孩子们发现分类的属性改变了，同样是5个人可以有两种不同的分类方法，其结果也是不同的。在这里只有当所有人都清楚要根据特定的属性来分成两个集合时，分类才真正开始。这是一个与现实生活密切联系的案例，案例中教师抓住契机发展幼儿的观察能力，促使他们更敏锐、多角度地思考事物的属性。

要点三：集合之间可以进行比较，以感知它们之间的关系

相关情景：活动室里，几个孩子在一起串木珠，方方发现了一个问题：“方块珠子没有了，我要的方块珠子不够了。”明明看了看放珠子的盘子，对方方说：“你可以用小星星来代替方块呀，这里有好多小星星珠子，比方块珠子多。”……

当一个整体被分成不同的集合时，幼儿和成人一样都会去进行比较。有时是比较哪个集合“更好”或者更让人喜欢，如“我喜欢猫，不喜欢狗”“木质玩具比塑料玩具好”“孩子们不喜欢用橙子作为水果点心”，等等，有时是对集合的数量进行比较，就像案例中的明明那样。5岁幼儿常常会比较日常生活中碰到的有关数量的问题：谁的更多？哪个更大？这样公平吗？这类数量比较会涉及不同集合之间的三种数量关系：……比……多；……比……少；……和……一样多。

幼儿需要更多的机会去感受物体是如何被分成不同的集合的，这样他们才能更容易去进行数量比较。在上面的案例中，盘子里的珠子已经被孩子们按照形状特点进行了分类，因此，明明一眼就看出小星星珠子比方块珠子多。在现实生活中，一般在作比较前必须先进行分类。例如，如果我们想知道今天是穿雨鞋的幼儿多还是不穿雨鞋的幼儿多，我们肯定要先把幼儿分成两类：穿雨鞋的幼儿一类，不穿雨鞋的幼儿一类。有时候，有些物体的属性是显而易见的，比如，哪些图画是用水笔画的，哪些图画是用蜡笔画的等，分类是为了更容易比较。

在不同集合的比较中，如果数量接近，要想更准确地知道哪组数量更多，最好的办法就是数数。数数比目测更有效，是因为它能排除视觉干扰，使人更清晰地感知需要比较的不同集合中的每个组成部分。因此，在一个数学资源丰富的活动室里，教师常常会运用“什么是一样多”之类的问题去评估幼儿的数数和分类能力的发展情况。

当幼儿创造或重组集合的能力越来越强时，教师就可以鼓励他们对更复杂的组合进行分类和比较，比如开展“鞋子分类”活动：每个孩子拿出一只鞋，大家在一块小地毯上把鞋堆放到一起。教师提问：“我们应该怎样重新整理这一堆杂乱的鞋子呢？”这时教师需要引导幼儿思考如何进行分类，如有的幼儿可能会将鞋子分成“靴子、运动鞋、其他鞋子”；有的幼儿可能会将鞋子分成“尼龙搭扣的、系鞋带、扣扣子的”……教师可以让幼儿把自己所作的分类画在一张图表中，对它们进行数量比较（例如，从多到少依次排列）。这种分类方法不同于二分法，可称为多样化分类，它为幼儿提供了更多讨论如何确定集合与分类属性的机会，同时还能加深幼儿对通过分类更快地进行数量比较的理解。可见，当集合中的物体属性变得更加复杂时，教师引导幼儿掌握多、少、相等的相关概念是很重要的。教师可以多用这类概念来帮助幼儿仔细思考物体数量间的关系。这其中，师幼之间有关数学概念的对话非常重要，它对巩固幼儿的分类和数数经验极有价值。

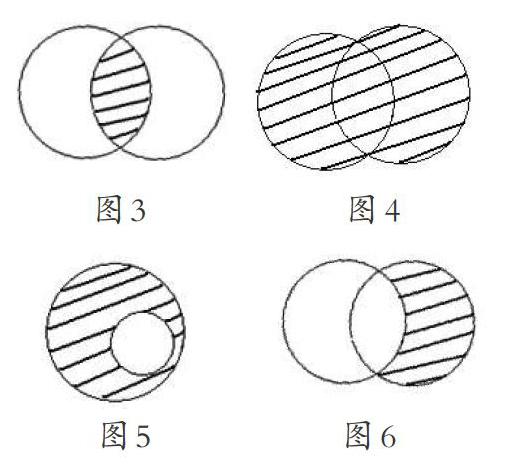
随着幼儿相关经验的积累，教师还可以引导幼儿感知不同集合之间的关系。一般说来，两个集合间存在着包含或相等关系。由同时属于两个集合的元素所组成的集合称为两个集合的交集（见图3）；所有属于两个集合的元素组成的集合称为两个集合的并集（见图4）；由全集中所有不属于该子集的元素组成的集合称为补集（见图5）；由属于一个集合而不属于另一集合的元素组成的集合称为差集（见图6）。教师可以充分利用幼儿的日常生活经验，加以适宜的引导，帮助年龄稍大的幼儿尝试着理解基于实际生活情境的集合关系，如在“人物分类”游戏中将两个呼啦圈相交（红色圈里站穿跑鞋的孩子，绿色圈里站戴眼镜的孩子），启发幼儿思考“既戴眼镜又穿跑鞋的孩子可以站在哪里”的问题，从中引导幼儿感知交集的概念；也可以引导幼儿给一堆包括有水生和陆生动物、四条腿和两条腿动物的图片分类，让幼儿思考后按照不同层级进行多次分类，并在分类中深入思考两栖动物该放在什么位置之类的问题，等等。需要强调的是，对于集合之间的抽象关系让幼儿纯粹靠记忆学习或通过成人的传授学习都是没有意义的，它需要幼儿与生活情境和问题背景相联系才有可能产生有意义的学习。