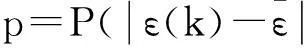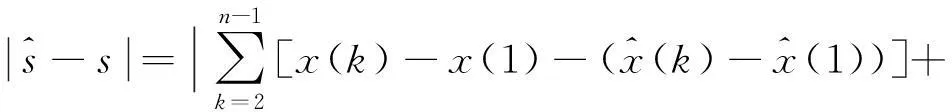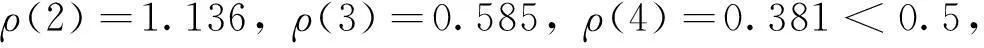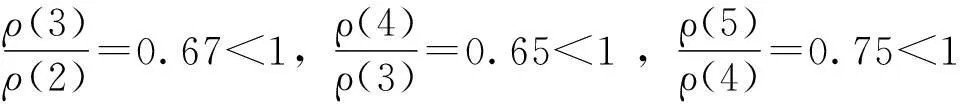基于灰色GM(1,1)模型的阶梯水价实行效果分析
2016-03-24栗嘉琨
栗嘉琨
(三峡大学 水利与环境学院,湖北 宜昌 443002)
基于灰色GM(1,1)模型的阶梯水价实行效果分析
栗嘉琨
(三峡大学 水利与环境学院,湖北 宜昌 443002)
摘要:现有文献对阶梯水价的研究集中于如何制定合理的阶梯水价,阶梯水价的可行性等方面,对于阶梯水价的实行效果没有统计分析。灰色GM(1,1)模型可以充分利用已有的城市供水量数据信息,分析其变化规律,对相同条件下的未来城市供水量做出预测。通过分析实例对比相同条件下实行阶梯水价和不实行阶梯水价时城市的供水量,得到的差值即为实行阶梯水价所节约的水量,结果表明这一预测模型合理有效。
关键词:管理科学与工程;节水效果;灰色GM(1,1)模型;阶梯水价
2002年4月1日,中国国务院国家计委、财政部、住房和城乡建设部、水利部、国家环保总局就联合发出《关于进一步推进城市供水价格改革工作的通知》,以下简称《通知》,要求进一步推进城市供水价格改革。《通知》要求全国各省辖市以上城市须在2003年底前实行阶梯水价,其他城市则在2005年底之前实行阶梯水价。从2002年至今,我国的深圳、银川等城市陆续实行了阶梯水价,阶梯水价的实行,不但有效的提高了人们的节水意识,而且在推动污水的再生利用,推广、更新节水器具等方面发挥不可低估的作用,体现了阶梯水价的价值所在。居民生活用水实施阶梯水价具有很多优点,但同时也存在着一些不足[1]。目前研究侧重于阶梯水价如何制定,如何实施,如何预测城市的用水量[2],却鲜有实行阶梯水价前后城市用水量的对比,而且对于阶梯水价的实行效果评价没有统一标准。对于阶梯水价的节水效果也没有科学的数据给予支持。因此,寻找一种评价阶梯水价实行效果的方法,不但可以对阶梯水价这一政策给予支持,也可以为更好地制定阶梯水价给予一定的支持。
1灰色系统预测理论
灰色预测运用序列算子对原始数据进行生成、处理、挖掘系统演化规律,建立灰色系统模型,对系统的未来状态做出科学的定量预测。具体采用什么预测模型,应以充分的定性分析为依据,选择适合的模型。建立模型之后,还要对模型进行多种精度检验以判定其是否合理、有效,只有通过检验的模型才能用于预测。
自20世纪80年代邓聚龙教授提出并建立了灰色系统理论以来,该理论已应用于农业、林业、气象、灾害、矿产的预测[3]。该理论不同于概率统计理论需要所有的训练数据集建立模型,是一种有效地处理不完全信息,解决不确定性问题的方法。在使用该理论建立预测模型前先消除原始数据的波动,就可以准确预测系统未来的发展趋势[4]。本文采用灰色系统理论,对阶梯水价实行前的用水量数据进行开发利用,预测阶梯水价实施后的用水量并与实际用水量进行对比,从而可以定量评价阶梯水价的实行效果。
2预测模型体系
针对要分析的具体问题,本文选择最常用的数列预测模型GM(1,1)模型。
2.1GM(1,1)模型建模条件
(1)原始序列光滑比检验。对于原始序列Χ=(x(1),x(2)……x(n)),由公式
(1)
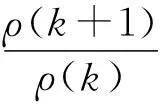
(2)一次累加生成序列准指数规律检验。对原始序列Χ=(x(1),x(2)…x(n)),由公式
(2)
计算其级别。
若∀k,σ(k)∈(0,1),则称序列具有负的灰指数规律;若∀k,σ(k)∈(1,b),则称序列具有正的灰指数规律;若∀k,使得σ(k)∈(a,b),且b-a=δ则称序列具有绝对灰度为δ的灰指数规律;当δ<0.5时,称序列具有准指数规律。
若有Χ(0)为非负准光滑序列,则Χ(0)的一次累加生成序列Χ(1)必然具有准指数规律。可以建立GM(1,1)模型。
原始序列的一次累加生成序列由公式为
其中
(3)
因此若第一步中原始序列满足光滑比条件,则不必再检验一次累加生成序列的准指数规律,可使用Χ(1)序列建立GM(1,1)模型[5]。
2.2模型建立
(1)对Χ(1)作紧邻均值生成。令
(4)
可得:Ζ(1)=(z(1)(2),z(1)(3)……z(1)(n))。
(2)建立模型。
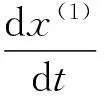
则GM(1,1)模型的最小二乘估计参数列满足
(5)
那么GM(1,1)模型的时间响应序列为
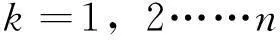
(6)
还原值即原始序列的模拟值为
(7)
2.3精度检验
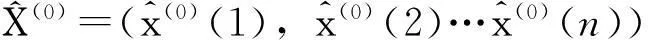
(8)
相应误差序列为
(9)
(2)原始序列的均值和方差为
(10)
残差的均值和方差为
(11)
均方差比值为
(12)
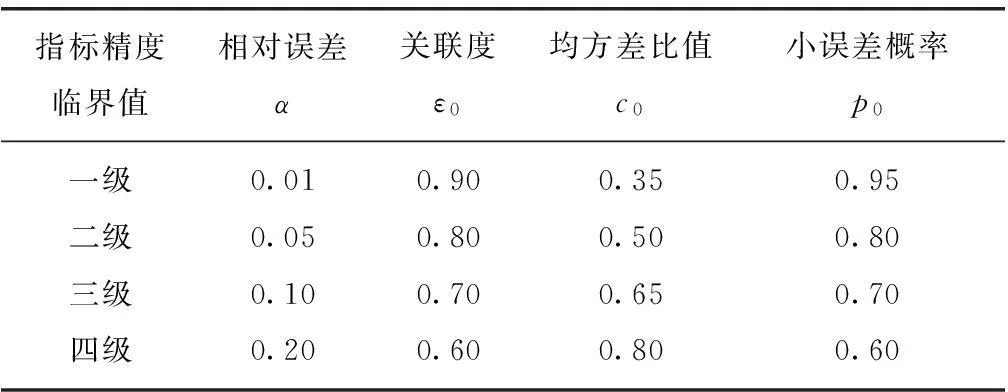
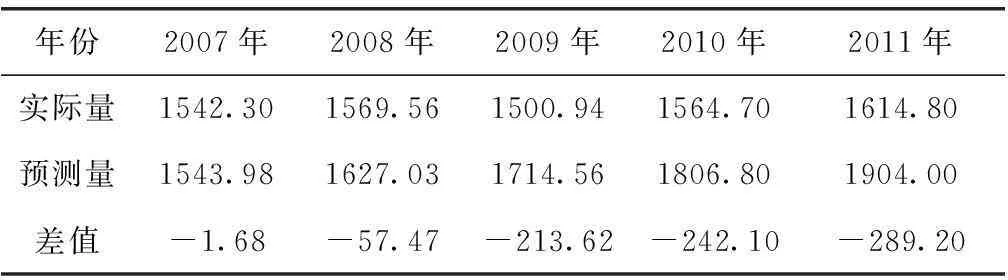
对于给定的C0>0,当C (3)小误差概率为 (13) 对于给定的p0>0,当p>p0时,称模型为小误差概率合格模型。 (14) 若对于给定的ε0>0有ε>ε0,则称模型为关联度合格模型[6-7]。上述进度检验指标的等级临界值见表1。 表1 精度检验等级参照表 2.4灰色GM(1,1)模型适用范围 当-a≤0.3时,可用于中长期预测;当0.3<-a≤0.5时,可用于短期预测,中长期预测慎用;当0.5<-a≤0.8时,做短期预测应十分谨慎;当0.8<-a≤1时,应采用残差修正GM(1,1)模型;当-a>1时,不宜采用GM(1,1)模型[8]。 3实例分析 以深圳市为例,运用2007年以前(阶梯水价实行前)的城市供水量数据序列建立GM(1,1)模型,对相同环境下2007年,2008年,2009年的城市供水量进行预测,并和实际供水量进行对比,评价阶梯水价的实行效果。深圳市城市供水量见表2。 表2 深圳市城市供水量[9] 106 m3 (1)对原始序列作光滑比检验。由式(1)计算得 ρ(5)=0.287<0.5 (2)对一次累加生成序列作准指数规律检验。由式(3)计算 Χ(1)=(1080.70,2308.65,3658.91,5053.78,6506.05) 由式(2)计算得σ(2)=2.136,σ(3)=1.585<2,σ(4)=1.381<2,σ(5)=1.287<2,当k>3时,σ(k)∈[1,1.5],δ=0.5,准指数规律满足,故可以对Χ(1)建立GM(1,1)模型。 (3)对Χ(1)作紧邻均值生成。由式(4)计算得Z(1)=(1694.67,2983.78,4356.34,5779.91)。 (4)建立GM(1,1)模型。由式(5)计算得a=-0.0524,b=1162.875,则GM(1,1)模型为x(0)(k)-0.0524z(1)(k)=1162.875。 (5)建立预测公式。由式(6)、(7)计算得 对照表1知模拟精度为较高级别,且发展系数-a=0.0524<0.3,此GM(1,1)模型可做长期预测。对深圳市供水量进行预测,预测结果见表3。 表3 2007—2011年实际与预测供水量的比较 106 m3 从实际供水量与预测供水量的差值可以看出阶段水价实行后的节水效果十分明显。 4结论 灰色系统预测理论所需要的原始数据少,模型精度合格后的预测精度高,因此适用于多个领域。本文采用深圳市的城市供水量作为实例分析,验证了灰色系统预测理论在评价阶梯水价实行效果中是切实可行的,预测结论符合实际情况,同时也为评价阶梯水价的实行效果提供了一定的科学数据。 参考文献: [1]李明,金宇澄.居民生活用水实施阶梯水价引发的思考[J].给水排水,2006,32(3):107-111. [2]师鹏飞,杨涛.深圳市用水量预测及情景分析[J].水电能源科学,2011,29(11):25-27. [3]Jun Lan,Hua xiang Cheng.The Grey System and Prediction of Geological and Mineral Resources [J].Mathematical Geology,1992,24(6):653-662. [4]Guo-Dong Li,Shiro Masuda,Chen-Hong Wang,et al.The hybrid grey-based model for cumulative curve prediction in manufacturing system [J].Int J Adv Manuf Technol 2010,47:337-349. [5]尹连生,白玉皎.GM(1,1)模型建模条件及模型改造[C]//中国土地学会.中国土地学会首届青年学术年会论文集,1992. [6]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010. [7]聂相田,李东亮.基于GM(1,1)——马尔科夫模型的城市用水量预测[J].华北水利水电学院学报,2011,32(2):5-7. [8]邓聚龙.灰色系统理论数据[M].武汉:华中理工大学出版社,1990. [9]深圳市统计局.深圳统计年鉴(2012)[EB/OL].(2012-11-20)http://www.sztj.com/main/index.shtml. The effect analysis of the cascade water price based on Grey GM(1,1) model LI Jiakun (CollegeofHydraulicandEnvironmentalEngineering,ChinaThreeGorgesUniversity,Yichang443002,China) Abstract:There searches about cascade water price focused on how to make the reasonable water price or the price ladder's feasibility, while there is no statistical analysis of the implement effect of the cascade water price. The Grey GM (1, 1) Model can fully use the existing urban water supply data, analyze their change rule, and then make predictions about the future of the urban water supply in the same conditions. Comparing the urban water supply with the implementation of the cascade water price and not under the same conditions, the difference is the water consumption saved with the implementation of the cascade water price. The example analysis shows that the prediction model is reasonable. Key words:management science and engineering;water saving effect; Grey GM(1,1) model;cascade water price 中图分类号:TV213.4 文献标志码:A 文章编号:2096-0506(2016)01-0031-04 作者简介:栗嘉琨(1990-),男,硕士研究生,专业为管理科学与工程。E-mail:596660198@qq.com