基于Kostiakov二参数入渗模型参数的BP预测
2016-03-24舒凯民樊贵盛
舒凯民 ,樊贵盛
(太原理工大学,太原 030024)
土壤水分入渗是指降雨或灌溉水等地面水转换成土壤水的过程,是农田水分循环的主要过程之一。土壤水分入渗是指表征入渗过程模型的参数,也就是说土壤入渗参数的确定也就是入渗过程的确定。土壤入渗参数直接影响到地面灌溉过程的水分分布和灌溉质量,是确定地面畦、沟灌合理灌水技术参数的依据。由于我国灌溉面积的97%均采用地面灌溉的灌水方式,故土壤入渗参数的准确获取和应用是提高我国农业灌溉质量和水管理水平的关键措施之一。尤其是现代地面灌溉过程模拟及其灌水技术参数的优化都依赖着土壤入渗参数的输入。因此,获得准确的土壤水分入渗参数,是提高灌溉质量和效率,实现农业水资源优化管理的前提。然而在实际的农业生产中,土壤水分入渗参数的实测存在着耗时、费力、设备技术复杂等问题,要得到精准的入渗参数难度颇大。
针对上面提出的问题,国内外学者进行了许多试验与探索。管孝艳等[1]以水量平衡方程为基础,提出采用IPARM方法建立沟灌Kostiakov-Lewis入渗模型参数的估算方法;王维汉等[2]在畦灌实验的基础上提出了工作量小,精度较高的线性回归法来估算土壤入渗参数;缴锡云等[3]通过数学推导,提出改进Maheshwari法来对土壤入渗参数进行直接计算;冯锦萍等[4]依据土壤理化参数与土壤入渗参数之间的相关性,建立起两者之间的多元线性传输函数。然而这些估算土壤入渗参数的方法都存在一定的限制条件,其参数获取难度较大,精度不高,在实际的应用过程中存在局限。为了揭示土壤入渗参数与土壤理化参数之间的非线性本质,同时解决前人预测精度低的问题,郭华等[5]通过建立非线性预测模型对冻融土的入渗参数进在实际的应用过程中存在局限。为了揭示土壤入渗参数与土壤理化参数之间的非线性本质,同时解决前人预测精度低的问题,郭华等[5]通过建立非线性预测模型对冻融土的入渗参数进行预测;武雯昱等[6]利用BP神经网络模型对Philip入渗半经验半理论模型参数进行预测。因而,本文基于大量大田入渗试验,利用BP神经网络模型在表达非线性、不确定性和模糊关系问题上的巨大优势,建立适用性较广的Kostiakov二参数入渗模型的入渗参数的BP测模型,即建立以土壤基本理化参数为输入变量,以Kostiakov二参数入渗模型参数为输出因素的BP神经网络预测模型,为获取准确的入渗参数提供技术手段,进而为提高农业灌溉水管理水平和灌水效率提供支撑。
1 材料与方法
1.1 试验土壤条件及数据样本
本文基于的试验数据样本来自山西黄土高原区大田耕作土壤入渗试验。试验地块一耕作大田土壤为主,但也有少量设施农业土壤, 耕作层深度一般为20 cm。试验土地土壤质地包括黏土、粉沙黏土、粉沙壤土、壤土、沙壤土等类型,其黏粒含量变化范围为0.9%~19.8%,粉粒含量为10.9%~76.0%。土壤状态分别为原茬地、翻松地和压实地,地表深度0~10 cm范围土壤的密度变化范围为1.0~1.6 g/cm3,10~20 cm土壤密度范围为1.101~1.536 g/cm3,犁底层20~40 cm土壤干密度变化范围是1.3~1.7 g/cm3。试验时耕作层体积含水率的变化范围为2.2%~39.6%,犁底层20~40 cm体积含水率变化范围是3.0%~49.9%。其土壤密度范围在地表深度0~20 cm范围土壤有机质质量分数为0.4~1.9 g/kg。本文所基于的试验土壤条件丰富,基本涵盖黄土高原区各种各种地貌单元土壤和土壤种类,代表性强。经过分析与筛选,选择具有代表性的110组数据样本建立模型,并预留10组进行精度检验。随机抽取其中3组数据的土壤常规理化参数见表1,Kostiakov二参数入渗模型参数实测值见表2。
1.2 试验设备与方法
本试验主要目的是为建立以土壤基本理化参数为输入变量,以Kostiakov二参数入渗模型参数为输出的模型提供样本。试验数据样本主要包括入渗参数与土壤基本理化参数。其中,土壤入渗参数用双套环土壤水分入渗仪获取。土壤入渗仪为自制的双套环入渗仪[7],其内环直径为26 cm,外环直径为64.4 cm,高度均为25 cm,试验前将双套环入渗仪埋设于大田试验点,深度达到犁底层。土壤入渗的试验时间控制在90 min,入渗开始后,采用分时段记录时间段与入渗量[8],试验时前15 min内,每1 min观测一次,10~70 min内,每5 min观测一次,70~90 min内,每10 min观测一次。大量试验证明,在试验开始后60 min时,大田土壤水分入渗基本可达到相对稳定入渗状态,为了确保任何一个试验达到相对稳定入渗状态,将入渗的时间控制在90 min。

表1 土壤基本理化参数表

表2 土壤入渗参数实测值
土壤基本理化参数的获取,包括土壤含水率、密度、质地、有机质等的测定。采用烘干称重的办法测的重量含水率,经换算得到体积含水率;用环刀法在各试验地点不同深度处进行土壤密度测定;在室内用比重计和筛分结合的方法测定耕作层与犁底层的颗粒级配,从而确定其土壤质地;采用重铬酸钾氧化法测定耕作层有机质质量分数,因而获得较为完整的土壤基本理化参数值。
1.3 Kostiakov二参数入渗模型
国内外专家学者提出了多种入渗经验模型,其中包括Philip入渗模型、Kostiakov三参数模型以及Kostiakov二参数入渗模型,在这3种经验模型中,二参数模型形式简单,计算方便,且模型拟合表明在0~90 min内,Kostiakov二参数模型的拟合精度要比三参数模型为高。考虑到灌溉的灌水时间一般小于90 min,本文对Kostiakov二参数入渗模型参数进行预报模型的建立与分析。模型形式为:
H=ktα
(1)
式中:H为任意时刻的累积入渗量,cm,t为时间,min;k为经验入渗系数,其物理意义是指入渗开始后第一个单位时段末的累积入渗量,在数值上与第一个单位时段末的入渗速度相等;α为经验入渗指数,反映土壤入渗能力的衰减速度。
分析可知,Kostiakov二参数入渗模型参数k与α值均随土壤基本理化参数的变化而变化,在不同的土壤条件下,k与α的取值情况即会发生变化,从而使得累积入渗量H也发生改变,最终形成不同情形的入渗状况。国内外学者对土壤水分入渗进行了大量研究试验,土壤本身性质是影响入渗状况的主要因素,其中质地、密度、初始含水率、有机质含量等是造成入渗差异的主要原因。
1.4 土壤入渗影响因素分析
研究发现,影响土壤入渗的因素很多[9-12]。首先是土壤质地:土壤质地越粗,其透水性越好,土壤入渗能力就大大提高,质地越细,孔隙越小,比表面积增大,其颗粒吸附能力越强,毛管力对重力的抵消作用也就越大,单位势梯度下,水分通量也就越小,入渗能力也就越差。其次是土壤密度:当土壤结构疏松,孔隙率大,孔隙之间的连通性好,因此对流动其中的水分阻力小,单位势梯度下的水分通量就越大;而随着密度增大,形成大量的土壤团聚体,从而使得土壤水吸力增大,透水性减弱,其土壤入渗能力大大减弱;再次是土壤含水率:初始含水率对土壤入渗影响较大,初始含水率较高的土壤,下面土层与饱和土层间的吸力梯度小,水分传导就会变慢,入渗速率就会降低,而对于初始含水率低的土壤,其下面土层与饱和土层之间的吸力梯度就大,水分下渗的驱动力增大,传导速度加快,土壤入渗的能力得到提高;土壤有机质也是影响因素:土壤有机质是土壤内部胶结物质,有机质含量越大,土壤团聚体数量越多,从而改善了土壤孔隙状况,使其更加稳定,土壤入渗能力也将得到提高,而对于有机质含量低的土壤,土壤结构性差且团粒结构不稳定,因而会阻碍土壤水分入渗,降低其入渗能力。
综上所述,本文选择了上述影响土壤入渗的多个主要基本理化参数,以其为输入变量,以Kostiakov二参数入渗模型参数k、α以及90 min累积入渗量H90为输出变量,建立BP神经网络预测模型,并验证其精度。从而实现基于土壤基本理化参数的土壤入渗参数预测。
2 BP神经网络的建立
2.1 输入变量与输出变量
由式(1)可知,k与α作为Kostiakov二参数入渗模型的经验参数,H为累积入渗量,将这三者作为BP神经网络的输出变量;同时,从前面的分析中可知,影响土壤水分入渗的基本理化参数包括有初始含水率、质地、土壤密度、有机质等,因此可作为BP神经网络的输入变量,由于水分通过地表进入土壤,地表对土壤水分入渗能力起控制作用[13],所以BP神经网络预测模型的输入变量为:耕作层(0~20 cm)含水率、0~20 cm土壤密度、0~20 cm黏粒含量与粉粒含量、0~20 cm有机质含量5个变量。
2.2 BP神经网络设计
BP神经网络一般具有3层或3层以上的神经网络结构[14],本文神经网络结构由输入层、隐含层及输出层组成。其中,输入参数有5个,故输入层的神经元个数为5,输出参数为3个,输出层神经元个数为3,中间隐含层神经元个数需要经过多次迭代计算才能得出,通过反复计算与迭代训练,最终达到精度要求时中间隐含层神经元个数为25,因此建立的BP神经网络拓扑结构为5∶25∶3。
在进行预测前,一般需要对样本数据进行归一化处理,从而使得 BP神经网络输入输出变量的数据在0~1之间,以确保输入输出变量的同等重要性。因此,选择学习速度较快、迭代误差小的trainlm函数为模型的训练函数,并利用MATLAB 7.0中归一化函数premnmx和还原函数postmam来实现对输入和输出样本的归一化处理,隐含层的激活函数为正切函数tansig,同时用线性purelin函数作为输出层的激活函数。本文模型参数设定为:最大学习迭代次数1 500次,学习率0.01,训练精度为0.000 5。
2.3 土壤入渗参数预报模型
根据土壤入渗样本利用软件MATLAB 7.0建立BP网络模型如下式:
net=newff[min max(trainput),[25,3],
{‘tansig’, ‘purelin’}, ‘trainlm’]
(2)
式中:net为所建立的BP神经网络;newff为MATLAB 7.0生成的BP神经网络函数;trainput为输入向量;min max(trainput)为输入向量范围;[25,3]为隐含层与输出层神经元个数,这里输出层3个变量分别为Kostiakov二参数入渗模型参数k与α值以及累积入渗量H;{‘tansig’,‘purelin’}分别为隐含层和输出层的激活函数;‘trainlm’为网络的训练函数。
BP神经网络的训练结果如下式:
[α,k,H]=purelin{iw2[tansig(iw1p+b1)]+b2}
(3)
式中:k、α与H为输出的土壤入渗参数;iw1为模型输入层到隐含层的权值;iw2为模型隐含层到输出层的权值;b1为模型输入层到隐含层的阈值;b2为模型隐含层到输出层的阈值;p=[θ,β1,β2,γ,Q],其中,θ为耕作层0~20 cm体积含水率,β1为耕作层粉粒含量,β2为耕作层黏粒含量,γ为耕作层土壤密度,Q为耕作层有机质含量。
BP神经网络预报模型iw1、b1组成的矩阵数值表见表3,iw2、b2组成的矩阵数值表见表4。
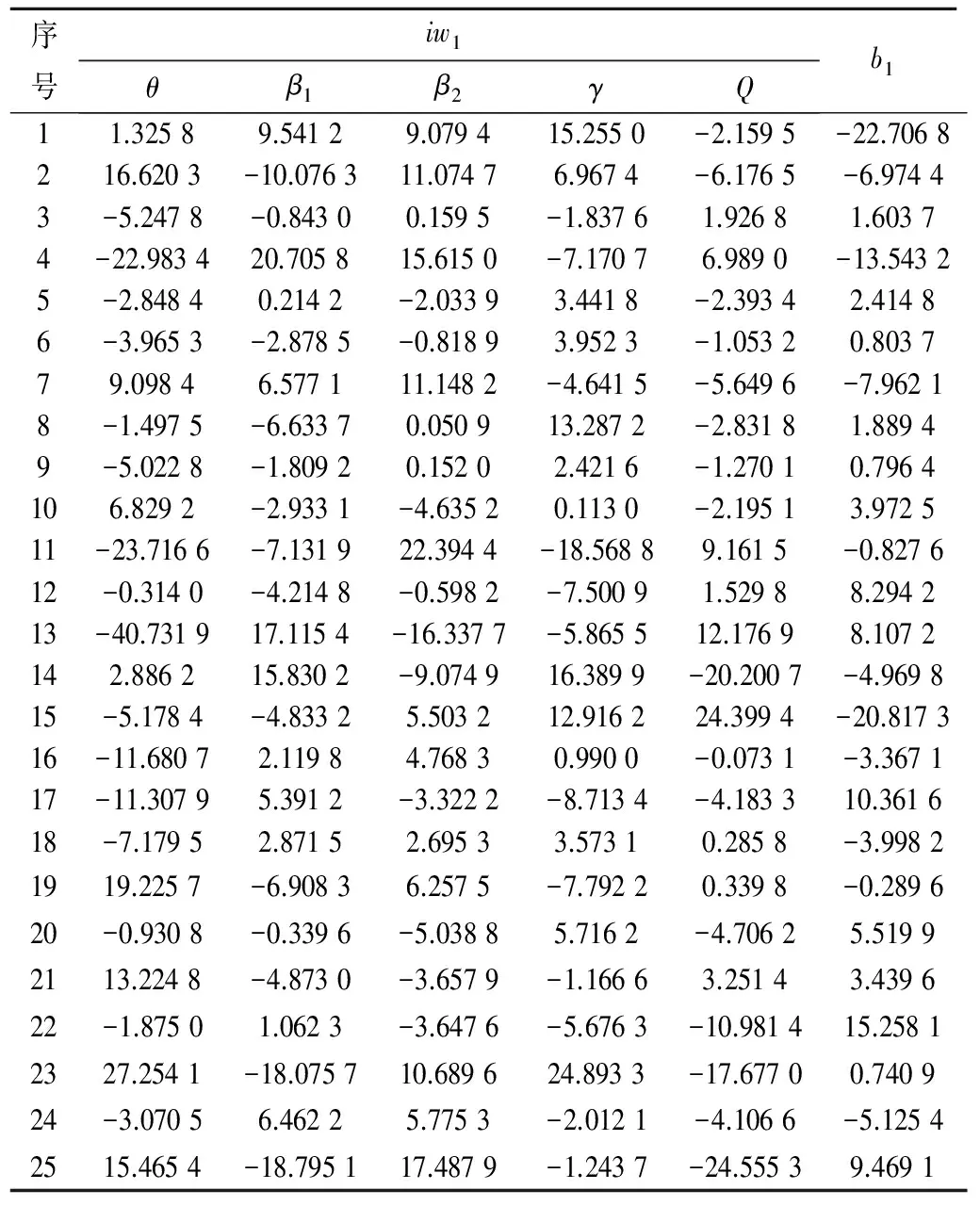
表3 BP神经网络输入层到隐含层矩阵数值表

表4 BP神经网络隐含层到输出层矩阵数值表
3 土壤入渗参数BP模型预测
3.1 Kostiakov入渗模型参数BP建模预测
用110组样本数据建立模型,利用MATLAB7.0程序进行BP神经网络预测,通过计算发现,当训练步数为717步时,训练精度为0.000 499 59,满足精度小于0.000 5的精度要求,证明用于建立BP神经网络模型的110组数据良好,与实测情况基本符合,精度较高。同时将得出的Kostiakov二参数入渗模型参数k与α以及90 min累积入渗量H进行精度对比,具体情况见表5~表7。

表5 入渗系数k预测结果与误差检验
从表5中看出,对于入渗系数k,其预测值与实测值的平均值相近,说明BP模型整体预测效果较好,同时BP预测模型相对误差平均值为6.140 5%,最大值为14.692 7%,最小值仅为0.032 1%,说明预测模型的精度较高,对入渗系数k的预测结果合理准确,满足训练精度要求。

表6 入渗指数α预测结果与误差检验
从表6中可以发现,入渗指数α的预测值与实测值几乎一致,说明对于α的整体预测结果十分准确,同时进一步分析,BP预测模型相对误差的平均值仅为1.045 9%,最大值为7.734 2%,最小值等于0,说明用数据样本建立的BP模型对入渗系数α的预测效果很好,训练精度高,实现较好的预测功能。
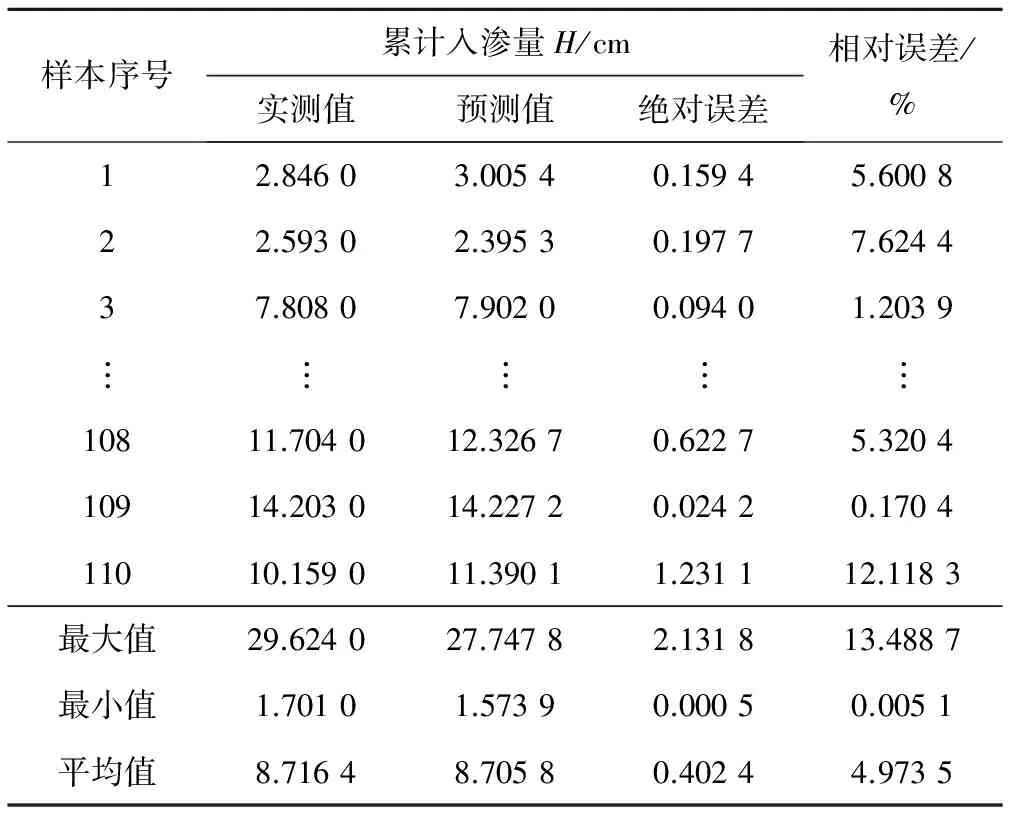
表7 累计入渗量H预测结果与误差检验
从表7中看出,对于90 min累积入渗量而言,实测值与预测值的平均值接近,BP预测对H的实现效果较好,同时还可以看到,相对误差的平均值为4.973 5%,最大值为13.488 7%,最小值为0.005 1%,相对误差值虽较前面入渗指数为大,但是整体而言误差较小,满足精度要求,实现了较为准确的预测效果。
3.2 BP预测模型检验
将预留的10组随机土壤样本对BP预测模型进行检验,并对比其精度,用以验证该BP预测模型的效果,实测值与预测值及相对误差对比情况见表8。

表8 BP预测模型精度检验表
从表8中可以看出,对于Kostiakov二参数入渗模型参数进行检验,证明BP预测模型的精度都较高,预测效果很好,检验时所有参数的相对误差均在3%以下,均略高于建模时的训练精度,说明本文所建立的BP预测模型在实际预测时可以达到较好的精度,预测模型可行性较强,故基于Kostiakov二参数入渗模型建立的BP预测模型具有较好的可信度。
4 结 语
采用BP神经网络方法,对Kostiakov二参数入渗模型参数进行建模预测是可行的,预测精度较高,预测效果较好。入渗系数k的平均相对误差为6.082 3%,入渗指数α的平均相对误差为1.045 9%,而90 min累积入渗量H的平均相对误差为4.973 5%,入渗指数α的预测结果最佳,入渗系数k次之,累积入渗量H误差最大,但此三者的相对误差值均在7%以下,都达到了很好的预测效果。
但是,本文所考虑的输入变量主要集中在土壤耕作层0~20 cm处,对土壤犁底层20~40 cm的土壤基本理化参数考虑不足。土壤理化参数对土壤入渗的影响作用十分复杂且涵盖深度较深,因此也存在个别预测值与实测值偏差较大的情况,在以后的研究中,可以进一步分析不同深度下土壤理化参数对土壤入渗模型参数的影响情况,从而确定更加合理准确的输入变量,使得预测精度进一步提高。
[1] 管孝艳,杨培岭,吕 烨.基于 IPARM 方法估算沟灌土壤入渗参数[J].农业工程学报,2008,24(1):85-88.
[2] 王维汉,缴锡云,彭世彰,等.畦灌土壤入渗参数估算的线性回归法[J].水利学报,2007,38(4):468-472.
[3] 缴锡云,王文焰,雷志栋,等.估算土壤入渗参数的改进Maheshwari法[J].水利学报,2001,(1):62-67.
[4] 冯锦萍,樊贵盛.土壤入渗参数的线性传输函数研究[J].中国农村水利水电,2014,(9):8-11.
[5] 郭 华,樊贵盛.冻融土壤 Kostiakov入渗模型参数的非线性预报模型[J].节水灌溉,2015,(11):1-4.
[6] 武雯昱,樊贵盛.基于Philip入渗模型的土壤水分入渗参数BP预报模型[J].节水灌溉,2015,(10):25-29.
[7] 曹崇文.利用土壤传输函数确定入渗参数的方法研究[D].太原:太原理工大学,2007.
[8] 李 卓,刘永红,杨 勤. 土壤水分入渗影响机制研究综述[J]. 灌溉排水学报,2011,(5):124-130.
[9] 解文艳,樊贵盛.土壤含质地对土壤入渗能力的影响[J].太原理工大学学报,2004,35(5):537-540.
[10] 解文艳,樊贵盛.土壤结构对土壤入渗能力的影响[J].太原理工大学学报,2003,35(4):381-284.
[11] 解文艳,樊贵盛.土壤含水率对土壤入渗能力的影响[J].太原理工大学学报,2003,35(3):272-275.
[12] 李雪转,樊贵盛.土壤有机质含量对土壤入渗能力及参数影响的试验研究[J].农业工程学报,2006,22(3):188-190.
[13] Magnus Porsson, Ronny Bemdtsson. Estimating transfer parameters in an undisturbed soil column using time domain reflectometry and transfer function theory[J]. Journal of Hydrology, 1998,205:232-247.
[14] 赵西宁,王万忠,吴普特,等.坡面入渗的人工神经网络模型研究[J].农业工程学报,2004,20(3):48-50.
