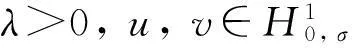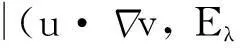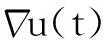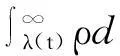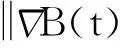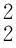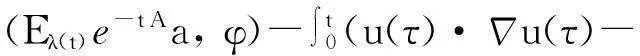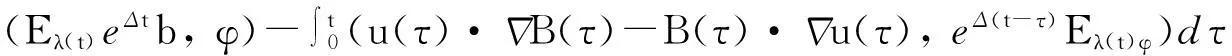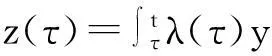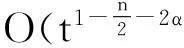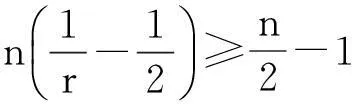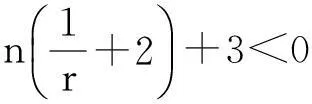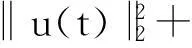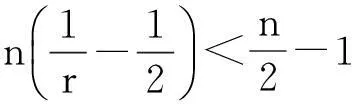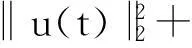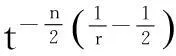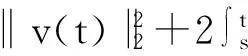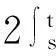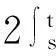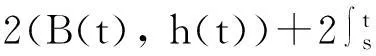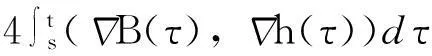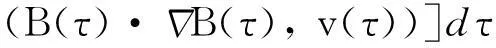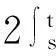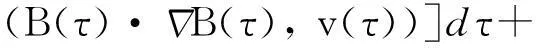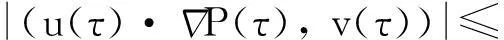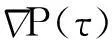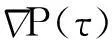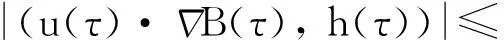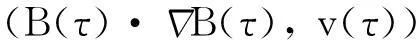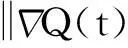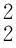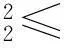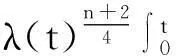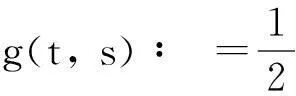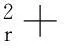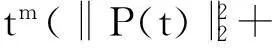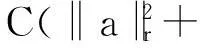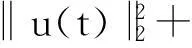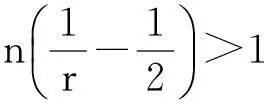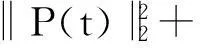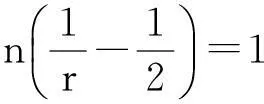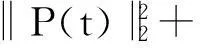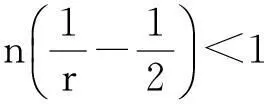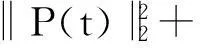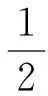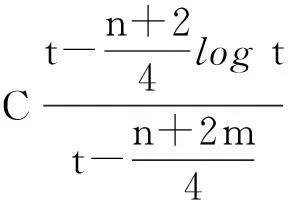半空间上MHD方程弱解的衰减下界
2016-03-24吕锴
吕 锴
(东华大学 理学院, 上海 201620)
半空间上MHD方程弱解的衰减下界
吕 锴
(东华大学 理学院, 上海 201620)
研究了磁流体力学(MHD)方程的弱解在半空间+上的衰减性质,通过建立一族产生弱衰减的初值, 得到了MHD方程的衰减下界.
磁流体力学(MHD)方程; 半空间; 衰减下界
磁流体力学(MHD)方程的一般形式为
(1)
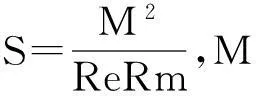
对于方程(1)的Cauchy问题,文献[1]构造了一类类似于Navier-Stokes方程的Leray-Hopf弱解的整体弱解.在全空间n上方程(1)的Cauchy问题的衰减性质的研究上,已有不少研究成果.文献[2-3]在文献 [4]的基础上研究了强解的衰减性质.而对于弱解的衰减性质的研究,可以参见文献[5-7].然而上述针对全空间n问题的结论,大多使用Fourier变换法,并不适用于半空间+∶={x=(x1,x2, …,xn)∈n;xn>0}问题.对于半空间上的MHD方程,文献[8]研究了弱解的L2衰减.文献[9]证明了当半空间上的Navier-Stokes方程(N-S)的初值在满足一定条件的情况下,可以得到N-S弱解的衰减下界的估计.本文在文献[9]研究成果的基础上,得到了半空间+上的MHD方程的相关结论.
(2)
1 主要结论
在介绍本文的主要结论之前,首先给出一些符号的定义.
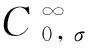
简便起见,将Ar简写为A.
下面给出方程(2)弱解的定义[10].
定义1.1 若(u,B)满足以下条件:
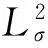

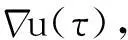
-(u(t), φ(t))+(u(s), φ(s))
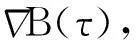
-(B(t), φ(t))+(B(s), φ(s)),
(3)
(iii) 能量不等式

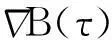
(4)
则称(u,B)为方程(2)在上的弱解.
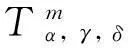
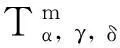

其中:m≥0, α, γ, δ>0.
假设 考虑满足以下条件的初值:
(A2)a′(x′,xn)=(a1(x′)η1(xn), (a2(x′)η1(xn), …,an-1(x′)η1(xn))∶=a″(x′)η1(xn)和b′(x′,xn)=(b1(x′)η2(xn), (b2(x′)η2(xn), …,bn-1(x′)η2(xn))∶=b″(x′)η2(xn),其中ηi∈L2(且满足对几乎所有的,都有,这里的表示ηi相对于xn的奇延拓,即

定理1.1 若n≥3,a,b∈Lr((满足假设(A1)~(A3),且r和m满足(i)或(ii):
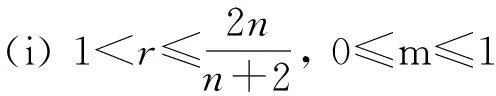

则存在T>1及常数C>0,使得当t≥T时,方程(2)的任意弱解(u,B)都有
(5)
定理1.1为本文主要结论.
2 Stoke方程及热方程解的衰减
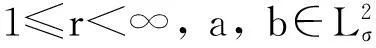

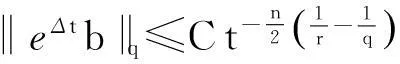
(6)
其中:q需满足1 (7) 其中:C=C(n, m, α, γ, δ)>0. 定理2.1[9]若n≥3,a满足假设(A1)~(A3),则当t≥1时,有 (8) 其中:C=C(n, m, α, γ, δ)>0. 定理2.2 若n≥3,b满足假设(A1)~(A3),则当t≥1时,有 (9) 其中:C=C(n, m, α, γ, δ)>0. 证明:因为bn≡0,所以有hn(t)≡0和h′(t)=eΔtb′.因此,由Plancherel定理和Fubini定理,有 (10) 对于I1,由引理2.1可知,存在C=C(n-1, m, α, γ, δ)>0,使得当t≥1时,有 (11) (12) 本节研究MHD方程解的衰减性质并给出定理1.1的证明.为了估计非线性项,首先给出以下引理. (13) 引理3.2 设1≤r<2 ,a,b∈Lr(对于方程(2)的任意弱解(u, B),当t→∞时,有 (14) 证明:设λ=λ(t)为(0, ∞)上的光滑函数,则 (15) 同理可得 (16) (17) (18) 由引理3.1,有 ‖Eλ(t)u(t)‖2≤‖e-t Aa‖2+ (19) ‖Eλ(t)u(t)‖2≤ (20) y(t)-g(t, s)+z(s)≤y(s) (21) z′(τ)=-λ(τ)y(τ)≤ -λ(τ)[y(t)-g(t, τ )+z(τ)] (22) 设Z(τ)≥0为方程Z′(τ)=λ(τ)Z(τ)的解,将式(22)乘上Z(τ),并对τ作(s, t)上的积分 (23) 对式(23)作分部积分,因为z(t)=0, g(t, t)=0,所以 (24) 取λ(τ)=m τ-1, m>0,则Z(τ)=τm.令s→0,得 (25) (26) (27) 下面将分情况进行讨论. 因此,有 引理3.3 若1≤r<2, a, b∈Lr(假设v(t)=e-t Aa和h(t)=eΔ tb,则对于方程(2)的任意弱解(u,B),当t→∞时,有 ‖u(t)-v(t)‖2+‖B(t)-h(t)‖2= (28) 证明:设P(t)∶=u(t)-v(t),Q(t)∶=B(t)-h(t), (u,B)满足能量不等式(4),v和h满足能量不等式 因此有 (29) 在式(3)中取试验函数φ(τ)=v(τ)和ψ(τ)=h(τ).此外,因为dv/dt=-Av,dh/dt=Δh,所以可得 (u(t), v(t))= (30) (B(t), h(t))= (31) 将式(30)和(31)代入式(29),有 (32) (33) ‖‖ ‖b‖‖u(τ)‖ (34) (35) 同理,由命题2.1,有 (36) (37) 设λ=λ(t)为(0, ∞)上的光滑函数,类似引理3.2中式(15)的证明,有 (38) 同理可知 (39) e-(t -τ)AEλ(t)φ)|dτ≤ (40) 同理有 (41) 类似引理3.2中的证明,可得 (42) 取λ(t)=m t-1,其中m>0足够大,有 (43) 此时注意到,若1≤r<2, (u, B)满足 下面将分情况进行讨论. 综上所述,引理3.3得证. 定理1.1的证明. 所以,存在T≥1,使得 再由三角不等式以及定理2.1和2.2,有 ‖u(t)‖2+‖B(t)‖2≥ ‖v(t)‖2-‖u(t)-v(t)‖2+ ‖h(t)‖2-‖B(t)-h(t)‖2≥ 综上所述,定理1.1得证. [1] DUVAUT G, LIONS J L.Inéquations en thermoélasticité et magnétohydrodynamique [J]. Arch Ration Mech Anal,1972,46(4):241-279. [2] ZHAO C, HE Y.GlobalLnstrong solutions to magneto-hydrodynamics equations in the Rnspace [J].Dyn Contin Discrete Impuls Syst Ser A Math Anal,2007,14(6):805-835. [3] LI Y, ZHAO C.Existence, uniqueness and decay properties of strong solutions to an evo-lutionary system of MHD type in R3[J].J Dyn Diff Eq,2006,18(2):393-462. [4] KATO T. StrongLpsolutions of the Navier-Stokes equations in Rmwith applications to weak solutions [J]. Math Z, 1984, 187(41): 471-480. [5] SERMANGE M, TEMAM R.Some mathematical questions related to the MHD equations [J].Comm Pure Appl Math,1983,36(5):635-664. [6] AGAPITO R, SCHONBEK M. Non-uniform decay of MHD equations with and without magnetic diffusion [J].Comm Part Diff Eq,2007,32(11):1791-1812. [7] GUO B, ZHANG L.Decay of solutions to magneto- hydrodynamics equations in two space dimensions [J].Pro R Soc Lond Ser A Math Phys Eng Sci,1995,449(1935):79-91. [8] 刘颖,李佳.半空间 MHD 方程组弱解的L2衰减 [J].数学物理学报,2010,30A(4): 1166-1175. [10] SCHONBEK M E, SCHONBEK T P,SÜLI E.Large-time behaviour of solutions to the magnetohydrodynamics equations [J]. Math Ann,1996,304(1):717-756. [12] BORCHERS W, MIYAKAWA T.L2decay for the Navier-Stokes flow in half-spaces [J]. Math Ann,1988, 282(1):139-155. 《东华大学学报(自然科学版)》征稿简则 《东华大学学报(自然科学版)》是由国家教育部主管、东华大学主办的以纺织、服装、纤维材料科学及相关学科为特色的学术性期刊(双月刊).从2008年起本刊栏目设有纤维与材料工程、纺织与服装工程、化学化工与生物工程、计算机与信息工程、机械与制造工程、环境科学与工程、经济与管理工程、基础科学,主要刊登本校师生的科学研究成果,适量刊登校外作者的优秀科技论文.本刊以高校师生、科研人员、工程技术人员及其他相关人员为读者对象.为保证刊物质量,根据国家标准和本刊的编排规则,特制定本简则. 1. 来稿要求 (1) 来稿要求论点明确、数据可靠、逻辑严密、文字精炼.来稿必须包括题名、作者姓名、单位及邮编、中英文摘要和关键词(3~8个)、中国图书资料分类号、第一作者简介(包括姓名,出生年,性别,籍贯,职称,学位,目前主要从事的研究方向及E-mail地址)、正文、参考文献.在文稿的首页地脚处注明论文属何基金项目资助及项目编号. (2) 论文摘要尽量写成报道性摘要,其内容独立于正文而存在,摘要内容应包括研究的目的、方法、结果、结论等要素,其长度一般在200字左右.中英文摘要一律采用第三人称表述,不要使用“本文”、“作者”等作为主语. (3) 论文篇幅(含图表)限7000字以内,科研简报限3000字.正文(含图表)中的量和单位的使用必须符合国家法定计量单位最新标准.文稿中外文字符的大小写、正斜体、黑白体、上下角标及易混淆的字母应打印清楚. (4) 正文中标题:一级标题1, 2, …;二级标题1.1, 1.2, …;三级标题1.1.1, 1.1.2, …;引言不排序. (5) 文中的图、表应有自明性,且随文出现.图、表应有中、英文名.插图须注意规范.如为坐标图,需用符号注明所表示的量(斜体)/单位(正体);如为照片,须黑白分明、层次清晰. (6) 参考文献应只列出作者查阅过的、最主要的且在正式刊物上发表过的文献.在正文中引用时用[1], [2], …顺序标注;在文末“参考文献”中,相应用[1], [2], …顺序标注,序号顶格写. 文后参考文献编排格式: ① 期刊:[序号]作者(姓前名后).题名[J].刊名(外文刊名可缩写),出版年,卷(期):起止页码. ② 专著:[序号]作者(姓前名后).书名[M].版本(第1版不写).出版地:出版者,出版年:起止页码. ③ 会议论文集:[序号]作者(姓前名后).题名[C]//编者.论文集名.出版地:出版者,出版年:起止页码. ④ 科技报告:[序号]作者(姓前名后).题名[R].报告题名,编号.出版地: 出版者,出版年:起止页码. ⑤ 学位论文:[序号]作者(姓前名后).题名[D].保存地点:保存单位,授予年份:页码. ⑥ 国际、国家标准:[序号] 主要责任者.标准编号,标准名称[S].出版地:出版者,出版年. ⑦ 专利文献:[序号] 专利申请者或所有者(姓前名后).专利题名:专利国别,专利号[P].出版日期. ⑧ 电子文献:[序号] 作者(姓前名后).题名[电子文献类型/标识](类型:数据库用DB,计算机程序用CP,电子公告用EB;标识:磁带用MT,磁盘用DK,光盘用CD,联机网络用OL).(发表或更新日期)[引用日期].电子文献的出处或可获得地址.建议在网址和相应的文献间建立起超链接. 文献作者3名以内全部列出,4名及以上只列前3名,后加“,等”或“,et al”. 2. 编辑部与作者的约定 (1) 本刊可接受网上在线投稿,在本刊的自动化采编系统完成投稿,凡初审符合要求的稿件,校内稿件每篇收取200元审稿费(东华大学校内经费卡转账),校外稿件每篇收取300元审稿费(将钱款邮汇到本刊编辑部).请勿一稿两投或多投.稿件经专家两审和编委复审通过同意发表,方可录用,对刊用稿件收取一定的发表费.凡不宜在本刊发表的稿件,编辑部将及时退还作者.如作者投稿4个月内未收到本刊编辑部任何通知,可自行处理稿件. (2) 为了适应我国信息化建设,扩大本刊及作者知识信息交流渠道,本刊已被国内外文献索引、文摘和全文数据库收录,作者著作权使用费与本刊稿酬一次性给付.如作者不同意文章被收录,请在来稿时向本刊说明,本刊将做适当处理. 编辑部地址:上海市延安西路1882号东华大学学报(自然科学版)编辑部(200051);电话:021-62373643, 62373724,传真:021-62373611;E-mail:dhutougao@126.com;网址: http://dhdz.cbpt.cnki.net Lower Bound of the Energy Decay of the Weak Solution of the MHD Equations in the Half-Space LÜKai (College of Science, Donghua University, Shanghai 201620, China) An asymptotic behavior of weak solution of the magneto-hydrodynamic(MHD) equations in the half-space+ is studied. By constructing a class of initial data which cause slow decay, lower bound of the energy decay of the MHD equations is obtained. magneto-hydrodynamic(MHD) equations; half-space; lower bound of the energy decay 1671-0444(2016)01-0160-07 2014-10-23 吕 锴(1988—),男,江西南昌人,硕士研究生,研究方向为磁流体力学方程.E-mail:faustxxiv@gmail.com O 175.14 A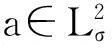
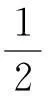
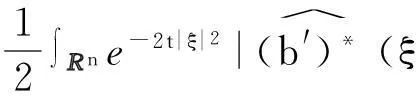
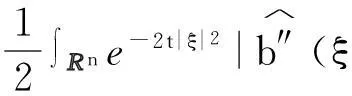
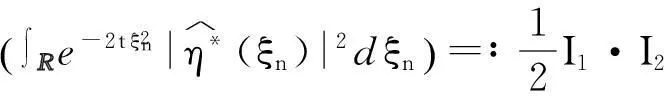
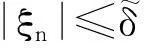
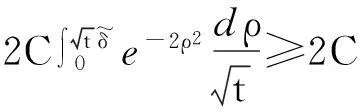
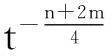
3 MHD方程解的衰减