例谈对应思想在教学中的渗透
2016-03-23姜达芹
姜达芹
[摘 要]对应思想是数学的基本思想方法之一,运用对应思想就是寻找对应关系,运用对应关系解决问题。教师要注重对应思想在课堂教学中的渗透,帮助学生全面提高数学素养。
[关键词]小学数学 课堂教学 对应思想 渗透
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)08-064
所谓对应思想是指在两类事物(集合)之间建立某种联系的思维方法,是数学的基本思想方法之一。运用对应思想解决数学问题可以化抽象为直观,化繁为简,发展学生思维,使学生的数学能力全面得到提升。下面我主要就对应思想如何在小数课堂进行渗透谈谈自己的教学体会。
一、在观察对比中渗透
对应思想为学生提供了思考问题的新视角。在关于数学知识的学习中,教师可以引导学生对不同层面的知识点进行观察、对照,学生观察越仔细,对问题的理解也就越深刻。因此,教师要善于引导学生站在对应的角度让学生对数学问题进行观察、探析等等,从而使对应思想在教学中得到有效渗透。
如教学“20以内的加法”时,虽然许多学生已经能够熟练进行20以内加减法的计算,但他们毕竟年龄小,灵活运用所学知识解决问题的能力还不高,容易出现各种各样的计算错误。
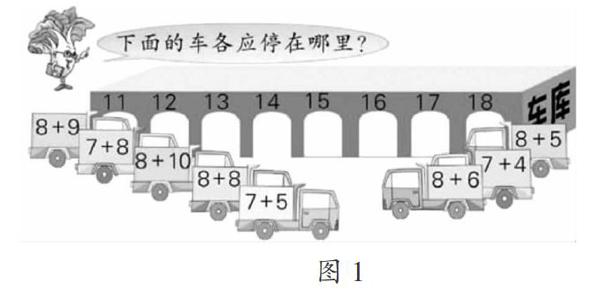
对于如图1所示的例题,怎样才能保证学生答题正确呢?教师可先向学生进行对应思想的渗透:让学生仔细观察图1,使其明白车库上面标注的数字是什么意思、各个加法卡片上面写的是什么、计算这些加法有什么用处等,帮助学生形成对应的思想。如此一来,学生解答问题的正确率有了明显提高。
上述教学案例中,教师没有急于让学生正确、快速地计算,而是把教学的侧重点放在了数学思想方法的渗透上。这样教学,既能够激发学生的学习兴趣、培养学生的观察力和想象力,又能使对应的思想得到有效的渗透,显著提高了教学效果。
二、在实际应用中渗透
学习数学的最终指向是学生的应用能力。教师如能把对应思想引入课堂教学中,不但可以简化教学过程,而且可以提高学生分析问题与解决实际问题的能力。
如教学“数据的统计与整理”时,当学生学完本节知识后,我让学生调查本班同学的视力情况,并做好关于视力的统计与整理工作。在教师的引领下,学生的调查结果如下:
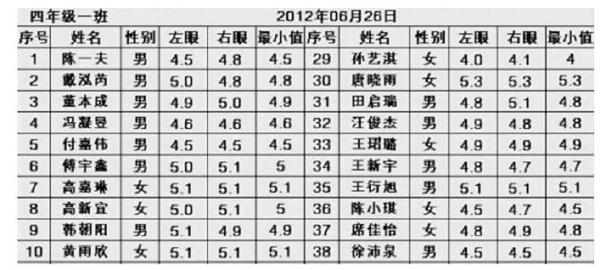
在学生统计汇报完毕以后,我就学生的统计结果让学生分别找出男生左眼视力在4.5以上的有几人、女生左眼视力在5.1以上的有几人……就这样,学生不仅完成了学习任务,而且建立起了一一对应的思想,深化了对所学知识的认识。
由此可见,在数学学习过程中,教师不仅要引导学生学会本节课的内容,还要向学生渗透相关的数学基本思想方法。长此以往,不仅可以提高学生的思想认识,还可以使学生触类旁通,有效地将知识进行迁移。
三、在数形结合中渗透
教学过程中,许多数学问题如果只是站在数的立场上,学生理解和解决起来会很困难。这时教师可以用图形表示数,或者通过数来对图形进行描述。
如对于“一条公路全长1200公里,已经修了400公里,余下的计划4天修完,求余下的每天修路多少公里?”这个问题,教师就可以引导学生从寻找对应关系入手,画出对应关系图,如图2所示。
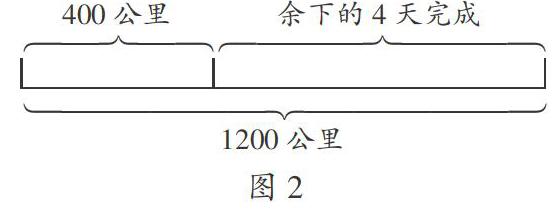
根据题意,结合该图,题目中各量的对应关系一目了然,解答起来也就简单许多。
在这个教学过程中,教师主要把对应思想引入其中,让学生从对应量与对应形入手,帮助学生建构图形,找出解题思路。这样解决问题直观、具体形象,可以使复杂问题简单化,降低解题难度,提高学习效果。
总之,教师要根据教学内容的需要,极力挖掘题目中的对应关系,渗透对应思想,拓宽学生的解题思路,使学生在学习过程中感受到数学的魅力,增强应用意识,提高学习效果。
(责编 吴美玲)
