少一点传道授业 多一些质疑多思

钱学翠

[摘 要]在小学数学课堂中，培养学生有效质疑的能力是课程标准的基本要求。从学生的认知入手，营造适宜的课堂氛围，让学生学会在已有知识的基础上质疑，从而获得解决问题的能力。

[关键词]质疑 课堂教学 能力

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）08-047

“学源于思，思源于疑。”教师应该鼓励学生大胆质疑，帮助学生在数学学习过程中获取知识，让学生学会在已有知识的基础上提出问题，又在数学活动过程中解决问题。

一、质疑习惯来源于氛围营造

小学生喜欢动手操作，喜欢表现自己，更喜欢自由表达。所以，给学生一个良好的课堂氛围，学生能够说出自己的想法，课堂就可以变成学生自由翱翔天地。

比如，在分数的教学中，教师首先出示一个三等分的圆饼状图形，然后出示“1/3”，问：“从这个图形中你能看出这个数字意味着什么？”学生回答十分踊跃，很快就得出“将圆形分成三等分，1/3表示一等分”。紧接着让学生用图形来表示他们所见过的分数。学生有的用剪刀将纸片剪成相等的份数，有的将绳子折叠成几折，有的将橡皮切成相等的几个小块，有的将数量相等的小棒分成几组，还有学生能够画图来表示分数……有个学生画了一个图形来表示1/3，引起了教师的注意，于是教师通过多媒体将图形展示出来（如右图）。

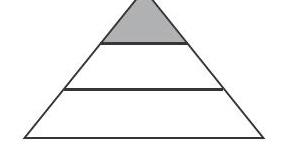
学生很快就觉得不对劲，但不知道问题出在哪里。于是教师让学生先展示自己做好的分数模型，再研究这个图形的问题。经过比较，很快就有学生提出：“必须将大的图形平均分成几等份才行！”学生顿时醒悟，对分数的定义理解得更透彻了。

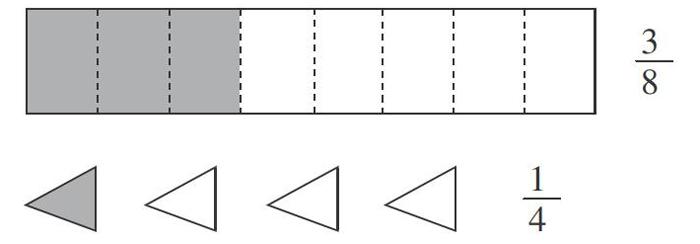
在教师的引导下，在教师精心创造的质疑氛围中，学生动手动脑，在活动中发现问题，独立思考，合作学习，从而解决问题。这样的教学方式让学生摆脱了灌输式的被动学习，也让教师摆脱了传道授业的传统模式，从讲台走到学生中间。

二、质疑内容来源于学生认知

一切质疑都是建立在原有认知的基础之上。学生对事物的认知或对事物的认知角度不同，质疑也就不尽相同。因此，不同的学生会有不同的思维模式或思维方法。

例如，在教学奇数与偶数时，教师给班上每个学生的胸前贴一个数字“0，1，2，3…”等，要求学生听口令站队。先要求胸前是偶数的学生站成一排。很快，胸前是2、4、6、7、10的学生站成了一排。教师提问：“这五个数中，哪一个数与众不同？”学生会质疑7为什么与众不同。但是不同的学生思考角度、原有认知都不同，所以有的学生会认为10与众不同，因为2、4、6、7都是一位数，而10是两位数。在原有认知的基础之上，学生的答案五花八门。不同的答案，说明学生的认知方式、认知水平不同，但有一点是相同的，即学生的思维是活跃的。此时教师本着绝不限制学生思维的原则，在夸赞学生的思维真不错的同时给出奇数偶数的定义。“自然数中，是2的倍数的数是偶数，不是2的倍数的数是奇数。”进一步得出结论：偶数=2乘任意一个数，奇数=2乘任意一个数+1，这里任意一个数是整数。”

紧接着，学生又有新的质疑：“0”号学生该站到哪一队去？

不同的思维，不一样的认知，让质疑一环扣一环，让学生不停歇地独立思考。有话想说，有话能说，这样的课堂极大地提高了教学质量，学生不再只是一个模仿者，而真正变成一个善于思考的“小科学家”

三、质疑效果决定于教师

1.质疑效果决定于教师的延迟判断

小学生的表现欲很强，教师可以利用这一优点来组织课堂。但是当学生产生不同意见吵着要表达，急着寻求教师的肯定时，教师要善于把握课堂。此时教师有必要延迟判断，与学生一起静下来，给学生更多的时间再斟酌，让学生获得更准确的表达。

比如，自然数和整数的学习过程中，一个物体也没有用0表示，0也是自然数。所以得出所有的自然数都是整数。那么，是不是所有的整数都是自然数呢？问题的提出引发了学生的争论，但此时的我只是静静地微笑，直至学生停止争论，达成共识。

可见，学生争相抢答时，教师做出的延迟判断，能为学生提供思考时间，提供心理安全的环境，让学生更为理智地发现自我、表现自我，从而高效地质疑。

2.质疑效果决定于教师能否融入学生

当然，教师的控制能力还表现在能否与学生一起质疑。学生的思考和判断能力是不可小觑的。当教师认为“自己是不懂的”，学生就会积极思考，来“教”或者“告诉”教师答案。

比如，分数教学中，“分母不可以是零”的教学，教师就可以故意装糊涂，来引导学生质疑“为什么分母不可以是零”。学生的答案很清晰：“任何数与0相乘的积只等于0，而不等于5。这就告诉我们，5÷0的商是不存在的，0不能作除数。”紧接着教师再糊涂一次：“因为0×0=0，所以0÷0=0。”但是学生的思考是有效的，他们坚决地回答：“必须有一个确定的数，使它与0相乘的积等于0，但是任何数与0相乘的积都等于0，这样的数有无数个。这就是说，没有一个确定的数可以作为0÷0的商，所以0÷0也是没有意义的。”

多年的教学经验证明，学生是有较好的反思意识和能力的。教师融入学生，也做“初学者”，站在“我是错的呀”的立场上与学生一起辩论、讨论，最终达成“咦，原来你是对的呀”，既能加深学生对概念的认识，也能培养学生数学问题解答的严密性和逻辑性。

3.质疑效果决定于教师的语言规范性

教师语言的不规范会给学生造成错觉，进而引导学生走进质疑的误区。小学生的表达能力还存在一定的障碍，所以教师需要在数学语言上下工夫，纠正学生数学语言不规范的缺点。

比如：“如果a÷b=c（a﹑b﹑c是不为0的自然数），a就叫做b的倍数，b就叫做a的约数。”教师要进行完整的表述，并突出整除及倍数和约数的相互依存关系，避免学生产生“把a叫做倍数，b叫做约数”的错误说法。

高效的质疑课堂的设计并不容易。教师既要提供可以质疑的内容，又要有效控制课堂，还需要注意数学语言的严谨性。在整个质疑过程中教师要解决的核心问题是要学生解决什么问题，“问题解决”的过程中学生应该质疑什么。少一点传道授业，多一些质疑多思，教师的精彩在于走下讲台，给学生更多的机会出彩！

（责编 童 夏）