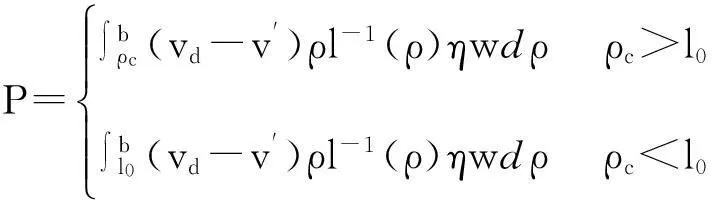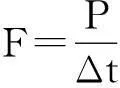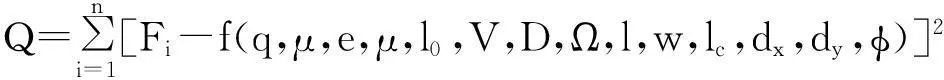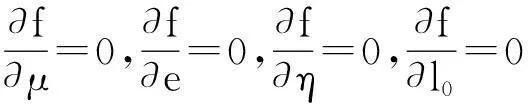基于动力学分析的谷物流量模型
2016-03-23胡静涛
王 鹤,胡静涛,高 雷
(1.中国科学院 沈阳自动化研究所,沈阳 110016;2.中国科学院大学,北京 100049;3.辽宁科技大学,辽宁 鞍山 114051)
基于动力学分析的谷物流量模型
王鹤1,2,3,胡静涛1,2,3,高雷1
(1.中国科学院 沈阳自动化研究所,沈阳110016;2.中国科学院大学,北京100049;3.辽宁科技大学,辽宁 鞍山114051)
摘要:基于运动学原理建立了谷物流量模型,该模型综合考虑了谷物流量测量时的外部因素影响,如升运器转速、机械结构参数、相对位置参数和谷物特性参数等,并且通过引进相关参数来反映谷物外部因素变化影响。为了实现谷物流量模型参数的辨识和模型的精度验证, 研制了一种谷物流量实验台。3个称重传感器安装在谷物流量实验台的称重箱上,用于标定和精度检验。进给箱的底部设有一块阀板,通过对阀板开度的调节可控制实验过程中不同进给量大小。在谷物流量实验台上测试结果表明:该模型能够准确描述:冲击力和谷物流量之间的关系,测量的最大误差不超过2. 5%,效果要优于常用的经验模型,并具有一定通用性和鲁棒性。
关键词:谷物流量模型;运动学分析;冲击力
0引言
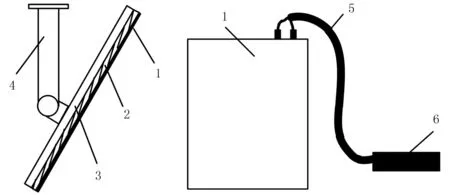
冲量式谷物流量传感器以其可靠性和安全性等优势近年来在测产系统中广泛应用[1-4]。这种传感器安装在收割机升运器的出口处,如图1所示。升运器抛出的谷物冲击在感应板上,引起弹性元件发生应变,此变形再经力敏元件转换成电量来反映谷物冲击力大小。当谷物流量不同时,冲击力也随之在一定范围内作近似线性变化。通过测量冲击力可对谷物流量进行估计。
1.冲量式谷物流量传感器 2.谷物 3.升运器
通常,谷物流量和冲击力或传感器输出的电信号的关系采用线性模型来描述,由于线性模型较为简单、建模容易,所以线性模型得到了广泛的应用。线性模型一般是对实验数据进行拟合来建立[5-10]。陈树人等[6]在静态下将谷物流量传感器横向放置,使冲击板保持水平,依次添加砝码并记录下砝码总质量和对应的输出电压值,根据记录下的数据进行建模;实验结果表明:测产最大误差为6.55%,平均误差为4.24%。王薄等[8]在自制的实验台上记录小麦实际质量与输出电压的累计量,通过试验数据可以发现:小麦质量与输出电压累计量保持一致的比例关系,所得到的拟合系数很稳定,因此可以采用平均拟合系数来建立线性模型;实验数据显示测产最大误差为5.44%,最小误差为2.07%。Loghavi等[9]通过实验发现谷物流量传感器采用多点拟合线性模的测量精度要好于两点拟合线性模型;多点拟合线性模最大测量误差为5.8%,两点拟合线性模型最大测量误差为8.3%。
线性模型的建立容易受实验条件的影响,如谷物流量不在标定范围就会产生较大的测量误差[10]。实验结果表明:在外部条件变化时(如升运器转速变化、较大的谷物流量),冲击力与谷物流量之间是非线性的[11]。所以,为了提高传感器的测量精度,研究人员考虑外部条件的影响并建立了非线性模型。邱白晶[12]等基于软球模型的离散元法,采用 Hertz-Mindlin接触力学模型模拟水稻籽粒流与承载板冲击过程,提出了在建立谷物流量模型时考虑如何减少谷物在谷物流量传感器上滑落阶段的影响;去除滑落阶段后,冲击力与谷物流量的线性关系有了很大的提高,从而提高传感器的测量精度。魏新华[13]在建立谷物流量模型时考虑了升运器转速影响,经过多次标定实验,建立一个以谷物流量为因变量,以冲击力和升运器转速为自变量的二元三次方程;试验结果表明:在不同升运器转速下,谷物流量范围为0.5~2.3kg/s时,最大测产误差不大于3.1%。Shoji[14]建立一种指数模型,并在模型中引入两个参数,并以标准差最小为目标优化两个参数,通过不同的优化参数以适应较大范围的流量变化,测量的最大误差为3.5%。
上述模型都是经验模型,且能够较好地估计出谷物流量。但是,经验模型中的参数没有明确的物理意义,使得外部因素对谷物流量的测量影响较大(如升运器转速、机械结构参数、相对位置参数和谷物特性参数),往往外部因素变化时需要对谷物流量传感器重新建模,降低了谷物流量传感器的通用性。根据上述模型中存在的问题,本文通过对谷物从抛出到撞击到谷物流量传感器的过程进行分析,基于运动学原理建立了一种谷物流量动态模型。谷物流量动态模型能够反映出冲击力与谷物流量之间的关系,模型中通过引进多个参数来反映外部因素的影响。
1谷物运动过程分析与建模
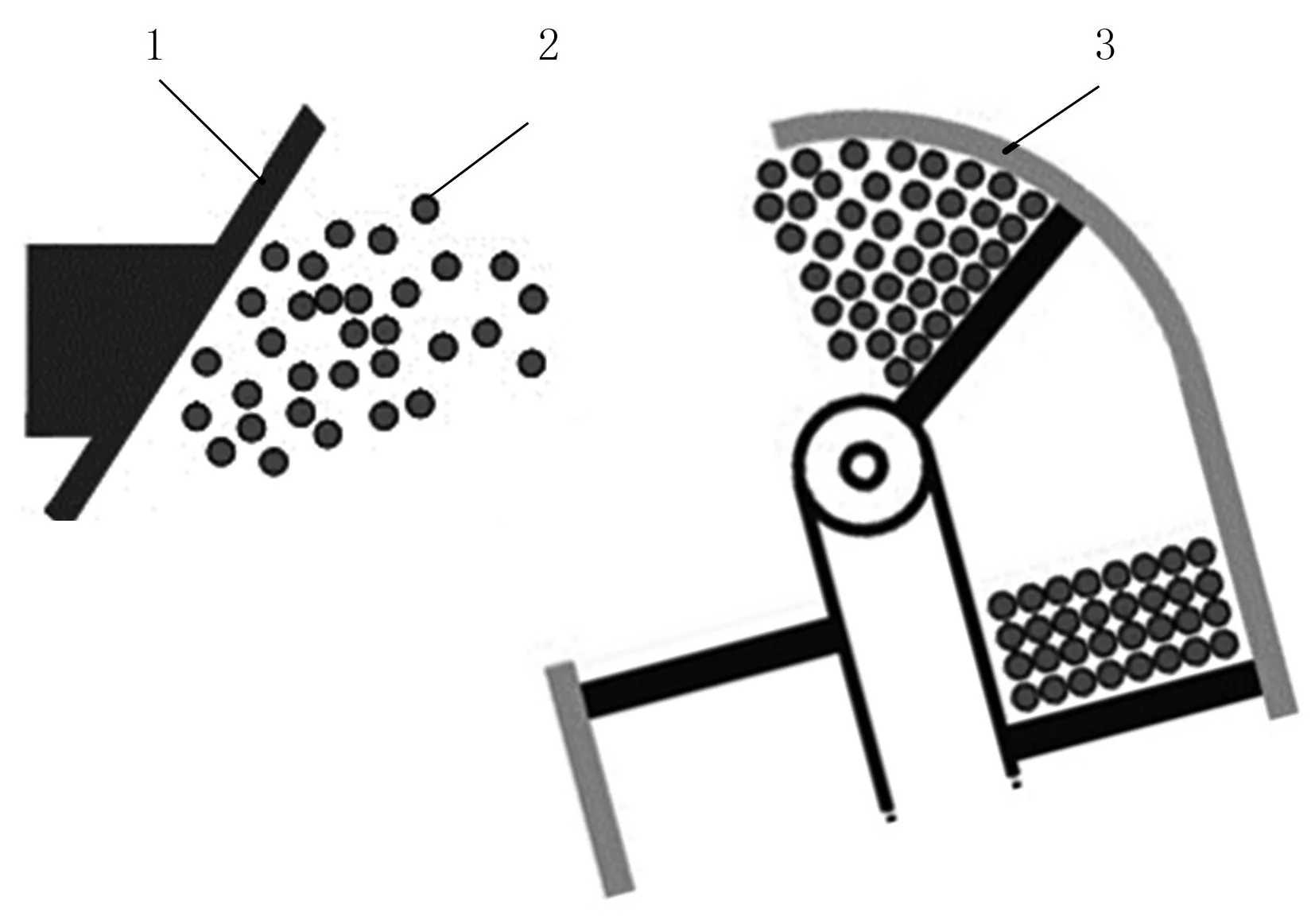
把谷物从抛出到撞击在谷物流量传感器上分为3个不同阶段(见图2)。①过渡阶段。谷物在刮板和升运器外壳的作用下,围绕着刮板旋转轴中心做圆周运动。在此阶段,假设没有谷物损失,并且谷物绕着刮板旋转轴中心的运动可以看作是刚体的定轴转动,即谷粒间的相对位置保持不变,各个谷粒的角速度相等,线速度与旋转中心距离成正比。②释放阶段。谷物脱离升运器外壳,只受刮板作用而不再受升运器外壳的约束,把释放阶段的谷物分割成角度区和径向层。在释放阶段的初始,谷物的径向速度由零变为非零,径向速度也与刮板旋转中心距离成正比,所以假设径向层的谷物之间没有力的作用,但角度区的谷物之间存在摩擦力。③飞行阶段。谷物不受任何限制和约束飞向谷物流量传感器。谷物飞行阶段的速度等于释放阶段末端的速度,由于谷物的速度较快,可假设谷物不受重力的影响。谷物与谷物流量传感器之间的碰撞属于弹性碰撞,并且符合冲量定理。
1.1 过渡阶段谷物内部边界分布规律模型
过渡阶段,谷物在刮板和升运器外壳联合作用下呈现一定的分布规律。文献[15]通过有限单元仿真表明:在此阶段中,无论谷物的数量多少,谷物的内部边界可以近似看作一条直线(见图3),并给出了谷物内部边界函数为

(1)
其中,l(φ)为谷物分布函数,表示谷物内部边界的点到旋转中心的距离;b为刮板宽度;φ为谷物内部边界上的任意一点到旋转中心的连线与刮板所成的角度;l0为谷物内部边界的最低点到旋转中心的距离;φm为谷物内部边界的最大角度。特别说明:当φ=0时,l(0)=l0;当φ=φm时,l(φm)=b。式(1)中,有3个参数φ、l0和φm,下面进一步推导l0和φm之间的关系,减少式(1)中的参数。
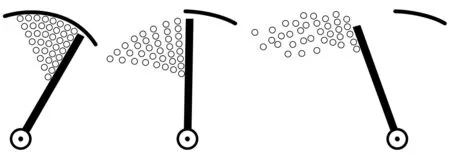
(a) 过渡阶段 (b) 释放阶段 (c) 飞行阶段
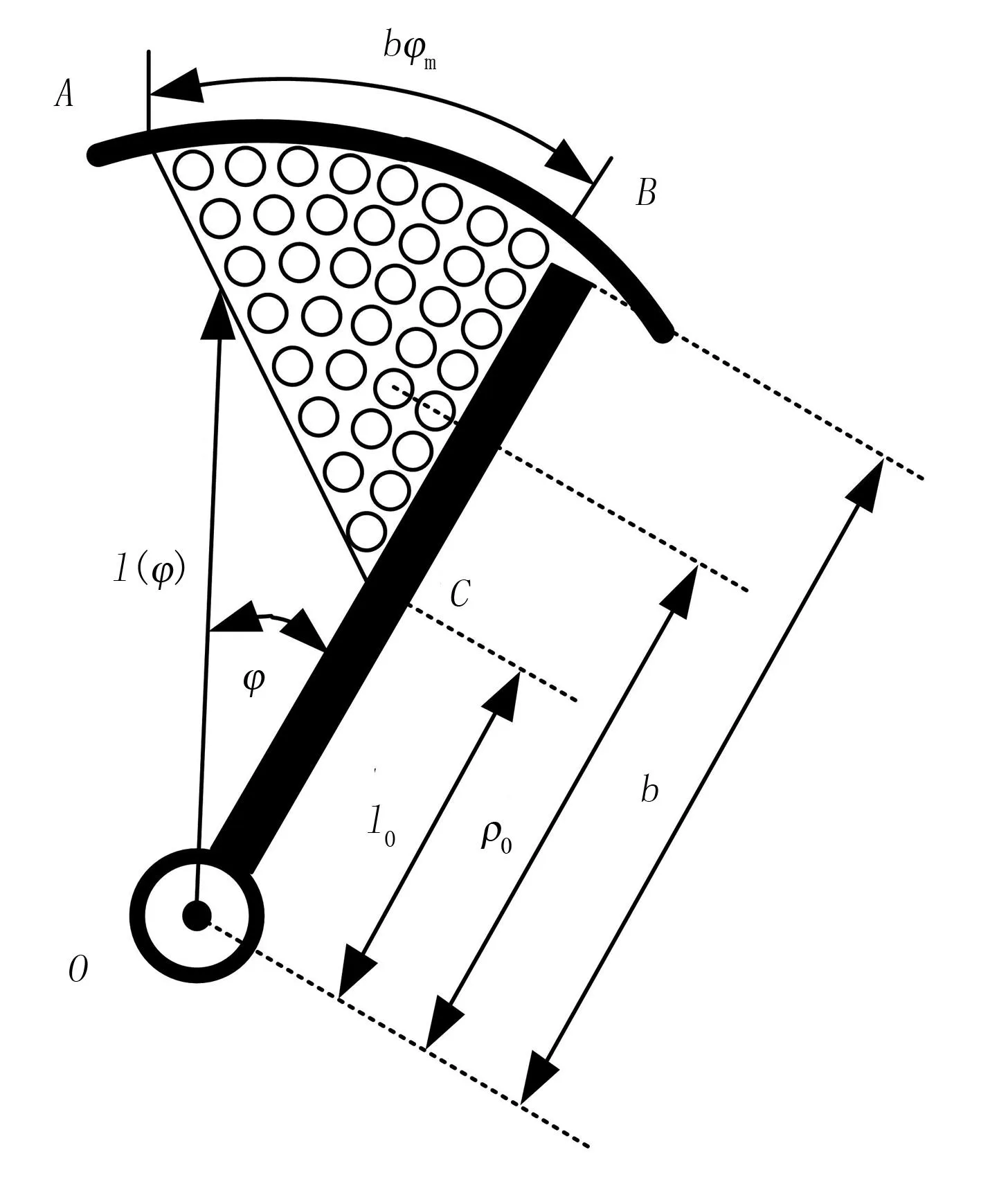
图3 过渡阶段谷物内部边界分布建模
谷物在此阶段的最大弧长为bφm,最大谷物厚度为b-l0,l0和φm两个参数可以描述谷物的形状,设谷物的形状系数为λ,则
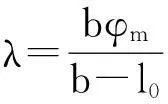
(2)
把式(1)中参数φm由参数l0代替,即

(3)
从而在谷物内部边界函数中只剩下一个未知参数l0,为了确定l0的大小,以谷物的截面积sABC为中间量,如图3所示,则
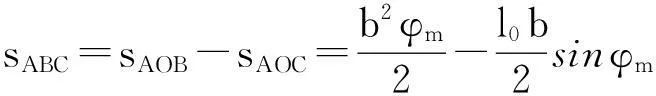
(4)
设刮板上谷物质量为M,那么谷物的截面积可表示为
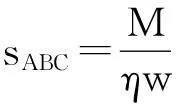
(5)
其中,sABC为谷物的截面积;η为谷物的体积密度;w刮板长度。由式(3)~式(5)可得
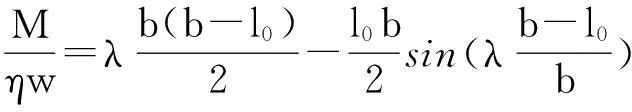
(6)
由于升运器转速快,刮板上的谷物质量M可认为与谷物流量传感器检测到的流量q相等。此外,文献[16]通过数值模拟发现谷物形状系数的值是约为2,式(6)又可变为

(7)
1.2 释放阶段谷物抛出速度模型
在释放阶段,谷物不再受到升运器外壳的限制,而是在刮板的作用和谷物间相互摩擦作用下,向外做加速扩散运动直到谷物到达刮板的末端。谷物间的相互作用主要产生在径向层之间和角度区之间,如图4所示。
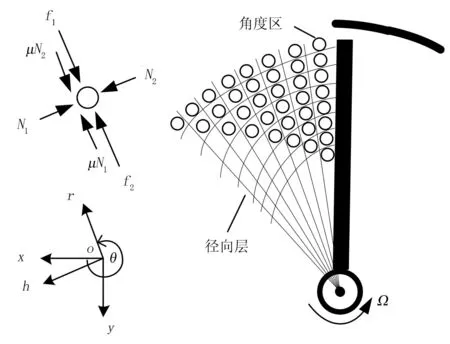
图4 释放阶段的谷物受力分析
图4中符号的具体含义如下:μN1、μN2为谷物之间的摩擦力;N1、N2为来自角度区谷物的压力;μ为谷物间的摩擦因数;f1、f2为径向层谷物的作用力;Ω是刮板旋转角速度;坐标系roh的r轴与刮板的宽度b方向重合,h轴垂直于刮板的宽度方向;坐标系xoy的x轴为水平方向,y轴为垂直方向。θ为两个坐标系的角度差,且θ=3π/2+Ωt。由牛顿第二定理可得
mar=f2-f1-μN2+μN1
(8)
mah=N2-N1
(9)
其中,m为单个谷粒的质量;ar为谷粒在r定轴方向的加速度;ah为谷粒在h轴方向的加速度。把式(9)代入(8)得到
m(ar+μah)=f2-f1
(10)
根据对释放阶段的分析,可以假设径向层之间的谷物不存在相互作用力,只存在角度区间的相互摩擦力。去掉径向层谷物间的作用力,式(10)可变为
m(ar+μah)=0
(11)
设er、eh和ex、ey分别为两个坐标系的基向量,则单个谷粒沿着刮板方向的位置可表示为
r=ρer=xex+yey
(12)
其中,ρ是单个谷粒到升运器旋转中心的距离。由坐标系转换可得

(13)
将式(13)对时间t求导得

(14)
联合式(13)和式(14)不难发现
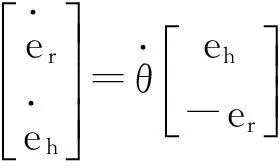
(15)
对式(12)求导,得到单个谷粒在坐标系roh内的速度为

(16)
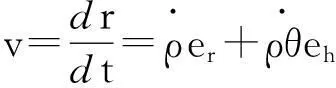
(17)
进一步对式(17)求导可得单个谷粒在坐标系roh内的加速度

(18)
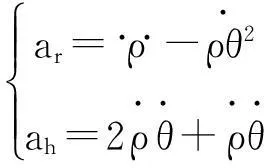
(19)

(20)


(21)
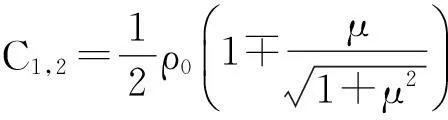
(22)
假设每个谷粒从过渡阶段的初始位置到达刮板末端的时间相同,并且设时间为td。td可由下式求得
ρ(td)-b=0
(23)
最后,在释放阶段的末期谷粒的速度可表达为
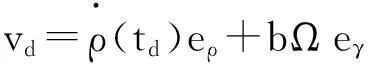
(24)
将速度转换到xoy坐标系中得
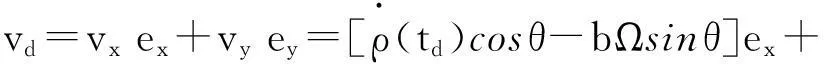

(25)
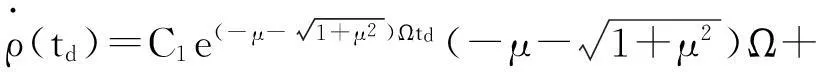

(26)
由式(22)~式(26)可知:在升运器转速一定情况下,释放阶段末期谷粒的速度主要由过渡阶段的初始位置ρ0决定,如图3所示。
1.3 飞行阶段谷物碰撞到传感器的条件
此阶段是谷物相互之间没有影响自由地飞向冲击板,如图5所示。图5中符号的意义如下:φ为传感器与水平方向的夹角;hy为升运器旋转中心到谷物流量传感器最低点的垂直距离;hx为升运器旋转中心到谷物流量传感器最低点的水平距离;β为传感器最低点到谷粒与谷物流量传感器碰撞点的距离;lc为谷物流量传感器的长度。在飞行阶段的初始,谷物的速度和位置等于释放阶段的末期速度和位置,并且谷物与冲击板撞击后符合冲量定理。

图5 飞行阶段
有研究表明:大约有15%~20%的谷物将不能达到传感器上[17]。为了计算施加在传感器上的冲击力,有必要确定与传感器碰撞的谷物比例。考虑到谷物从刮板到冲击板的飞行时间较短,可以忽略重力对飞行轨迹的影响。那么,谷物在飞行阶段的运动可以看作速度不变的直线运动。谷物能否与冲击板碰撞由谷物在释放阶段末期的位置和速度共同决定。由上节分析可知,这两个量又由谷物在释放阶段初始位置ρ0决定的。所以,这里设定一个谷物初始位置阈值ρc,当谷物初始位置ρ0>ρc时,谷物能够到达传感器;而ρ0<ρc时谷物将错过传感器。下面推导决定阈值ρc的条件。
在飞行阶段,单个谷粒从离开刮板飞向传感器的轨迹可表示为
straj=(bcosθ+vxt)ex+(-bsinθ+vyt)ey
(27)
其中,t为谷物离开刮板到达传感器所用的时间,特别当t=0时代表了谷物在释放阶段末期的位置;b是刮板的宽度;vx、vy为谷物在释放阶段末期的初始速度。同样,传感器的几何形状可由一条线段来表达,有
sstru=(hx-βcosφ)ex+(hy-βsinφ)ey
(28)
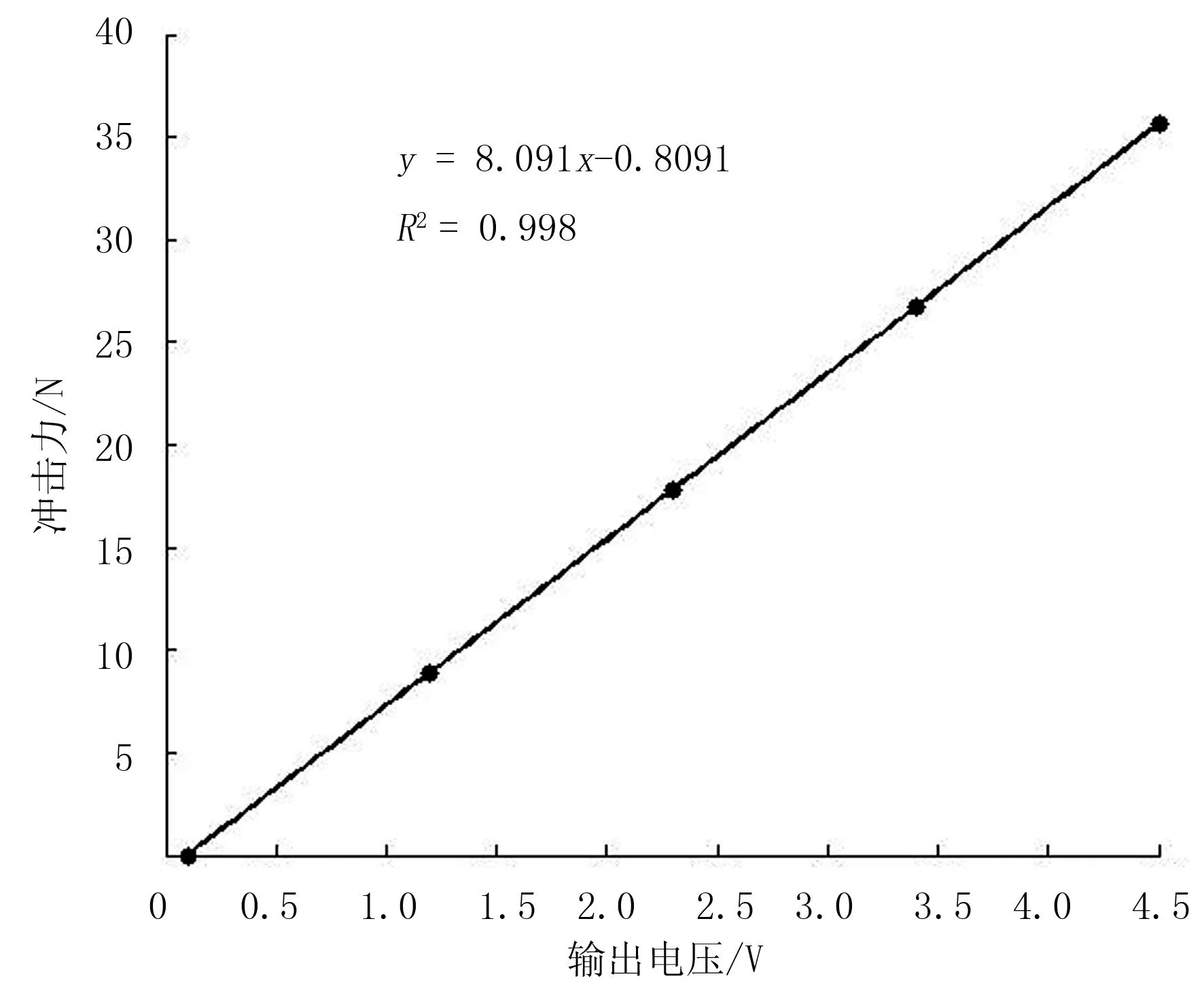
其中,β为传感器最低点与撞击点之间的距离,且0<β (29) 对式(29)求解得到 (30) (31) 由此谷物能够冲击到传感器上的条件为t>0和0<β 谷物与传感器碰撞过程中,冲击力和碰撞速度的变化都非常复杂,在分析谷物与传感器碰撞现象时,首先作如下假设:①谷物与传感器的碰撞属于弹性碰撞,即恢复系数0 对于假设1实际的碰撞一般都属于这一类。碰撞物体的动能因引起振动而失散,物体的变形不能完全恢复,或伴有内阻引起的能量损失。谷物与传感器碰撞时,能量交换主要发生在垂直于传感器方向上,如果传感器表面光滑,在平行于传感器方向上基本没有能量损失,所以假设2很容易满足。总之,这两个假设并不会使所建立的模型失去一般性。 谷物与传感器碰撞前的速度在释放阶段已求出,即vd。设谷物与传感器碰撞后的速度为v′,则碰撞前后的速度在xoy坐标系中可表示为 vd=vxex+vyey (32) (33) 设垂直于传感器方向上的基向量为n,如图6所示,那么 n=-sinφxex+cosφey (34) 谷物碰撞前的速度在垂直传感器方向上的分量可表示为 vd·n=-sinφxvx+cosφvy (35) 而平行于传感器方向上的速度可表示为 n×(vd×n)=(vxcos2φ+vysinφcosφ)ex+ (vysin2φ+vxsinφcosφ)ey (36) 根据假设1和假设2分别可得到 vd·n=-ev′·n (37) n×(vd×n)=n×(v′×n) (38) 式(37)中,e=es/eg为综合恢复系数;es为碰撞恢复系数,代表了谷物与传感器碰撞时的能量损失;eg为作用恢复系数,代表了谷物达到传感器之前,谷物间的相互作用造成能量损失。将式(35)和式(36)分别代入式(37)和式(38)得 (39) (40) (41) (42) 图6 谷物撞击传感器后的速度模型 由过渡阶段得到的谷物内部边界函数、释放阶段推导出谷物的速度以及飞行阶段的谷物碰撞后速度和谷物冲击到传感器上的条件,综合3个阶段的结果可得到传感器上获得的总动量为 (43) 其中,l-1(ρ)是谷物内部边界分布的逆函数,这里l-1(ρ)=φ。由于ρl-1(ρ)dρ是径向层的面积单元,如图7所示。所以,ρl-1(ρ)wdρ是径向层的体积单元。在冲击板上的谷物冲击力为 (44) 其中,F为作用在冲击板上的谷物冲击力,Δt=D/V,D是两块刮板之间的距离,V是刮板线速度。 图7 径向层面积单元 2模型参数辨识 根据谷物在各个阶段的模型和相关参数,对式(43)和式(45)进行简化,有 F=f(q,μ,e,η,l0,V,D,Ω,l,w,lc,dx,dy,φ) (45) 模型中包含了谷物特性参数(如μ,e,η,l0),相对位置参数如(dx,dy,φ),升运器结构和工作参数V,D,Ω,l,w,lc。其中,谷物特性参数无法直接测量,需要对其进行辨识。 如果给定冲击力、谷物流量和谷物的外部条件就可对模型中的谷物特性参数进行辨识(见图8)。对于谷物流量动态模型中参数的辨识同大多数动态测试数据处理问题一样,可借助曲线拟合法来解决。拟合法主要应用各种广义回归分析方法。在拟合代数多项式或更一般的广义多项式时,常采用传统的最小二乘法。由于外部条件的变化使冲击力与谷物流量之间由于外部条件变化存在非线性关系,故可建立二者之间的非线性回归模型并用非线性最小二乘法估计谷物特性参数。根据最小二乘原则使回归误差平方和为最小,对于式(45)则有 (46) 式(46)想要达到最小值,必须满足条件 (47) 式(47)将计算最优解的问题转化为求解非线性方程组的问题。非线性方程组不便直接求出参数的精确解。因此,通常要采用迭代法或最优化方法来求得近似解,这里采用牛顿迭代法求非线性方程组的解。 图8 模型参数辨识的输入输出 实际辨识时,首先把冲击力分为了不同区间,然后通过非线性最小二乘法和已知谷物流量辨识冲击力区间内相应的谷物特性参数。采用模型对谷物流量进行估计时,由于式(45)是非一个非线性方程,一般对非线性方程的求解一般有对分法、迭代法和牛顿法等。这里采用对分法对谷物流量模型进行求解,主要是考虑了对分法的计算简单、方法可靠及计算速度快的优点。所以,在冲击力测量值和相关模型模型参数已知情况下,根据测量的冲击力通过模型可对谷物流量进行估计。 3测产实验 谷物流量实验台上进行实验验证,实验台组成如图9所示。工作时,输送搅龙在异步电机的驱动下,将从存储箱中漏下的谷物输送到升运器,再由升运器将其提升并抛撒到称重箱中,以模仿谷物在联合收割机内的输运过程;调节阀板开度可改变谷物进给量,通过变频器调节异步电机转速可改变谷物的升运速度。 本文所采用的自行开发研制的冲量式谷物流量传感器,具体结构如图10所示。传感器具体包括:PVDF压电薄膜、阻尼材料、承载板、固定调整架和前置电荷放大器。PVDF压电薄膜通过针状金属端子作为电极并用屏蔽线引出接入前置电荷放大器,几何尺寸为220mm×180mm×0.07mm、压电常数d33为200pc/N。整张PVDF压电薄膜敷贴在承载板上,承载板的另一面设有固定调整架。PVDF压电薄膜通过固定调整架安装在收割机提升器的出口处,并且利用固定调节架上的定位孔来调节PVDF压电薄膜的安装角度和高度。在承载板和PVDF压电薄膜之间敷贴了阻尼材料,构成了自由阻尼结构。经过标定,冲击力与电荷放大器输出的电压之间呈现较高的线性关系,如图11所示。 1.称重传感器 2.均粮搅龙 3.称重箱 4.支撑机架 5.存储箱 (a) 传感器机械结构 (b) 传感器电气结构 图11 冲击力与输出电压关系 升运器转速传感器采用SZGB-6型光电转速传感器,测速范围为1~30 000r/min;检测距离最大为150mm;输出信号幅值为5±0.5V对应“1”, 0.5V以下对应“0”;谷物含水率传感器采用型号为HM1500,测量范围为0~100%RH,测量精度:≤±3%RH;谷物流量传感器和称重传感器的输出信号由NI USB-6216多功能数据采集卡进行采集。实验应用程序采用 LabVIEW 开发而成,谷物流量传感器和称重传感器的输出信号的同步采集、记录和分析。 在上述的实验台上进行模型验证实验:通过变频器把升运器转速调整为320、360、400r/min3个等级,在每个升运器转速下通过调整阀板的开度得到4种不同的谷物流量,测试重复3次,冲击力和谷物流量3次测试的均值作为真实值。模型中的相关几何相对位置和参数如表1所示。 表1 模型中相关参数 将上述参数代入谷物流量动态模型中,并根据传感器上测得的冲击力,按照模型估计谷物流量,实验结果如表2所示。 表2 不同升运器转速下对谷物流量估计结果 续表2 从表2中看出:在同一含水率下,冲击力随着升运器转速的增加也略微增大。这是因为升运器转速增加使谷物的撞击前的速度增大,根据冲量定理,当谷物撞击后的速度一定时,冲击力与撞击前的速度成正比,所以冲击力随着升运器转速的增加而增大。 4结论 1)在动力学理论下建立了一种谷物流量动态模型,模型分为3个阶段:过渡阶段、释放阶段和飞行阶段。模型准确描述了冲击力和谷物流量之间的关系,通过测量冲击力可以求出谷物流量。 2)谷物流量模型中引入了一些参数可以反映谷物的外部因素变化,如机械结构参数、相对位置参数和谷物特性参数等。模型中参数物理意义明确,目前模型中的未知参数在实验水平下可以获得。当传感器的安装点的几何形状发生变化时,调整模型中相应的参数,谷物流量传感器可以继续测量,不必重新标定建模,使谷物流量传感器具有了鲁棒性和通用性。 3)采用所建立的模型对谷物流量进行测量具有较好的精度,在谷物流量范围为 0.8~2.4kg/s时,测量的最大误差不超过2.5%,并且外部因素变化时能够保持测量精度的稳定。该模型为谷物流量测量提供新的理论基础。 参考文献: [1]Zhou J, Cong B, Liu C.Elimination of vibration noise from an impact-type grain mass flow sensor[J].Precision Agriculture, 2014,15(6):627-638. [2]丛秉华,周俊.双平行梁谷物流量传感器振动噪声消除方法[J].传感技术学报,2013,26(3): 377-381. [3]胡均万,罗锡文,阮欢,等.双板差分冲量式谷物流量传感器设计[J].农业机械学报,2009,40(4):69-72. [4]Fulton J P, Sobolik C J, Shearer S A, et al.Grain yield monitor flow sensor accuracy for simulated varying field slopes[J].Applied Engineering in Agriculture, 2009, 25(1): 15-21. [5]Hemming N, Chaplin J.Precision of real time grain yield data[C]//Proceedings of 2004 ASAE annual international meeting,2004:747-756. [6]陈树人,仇华铮,李耀明,等.谷物流量传感器试验台的设计与试验[J].农业工程学报,2012,28(16):41-46. [7]吕佐朝,邱白晶,房义军,等.承载板式谷物质量流量传感器设计与试验[J].农业机械学报,2011(S1):90-93. [8]王薄,李民赞,张成龙,等.冲击式谷物流量传感器设计与性能试验[J].农业机械学报,2009(S1):52-56. [9]Loghavi M, Ehsani R, Reeder R.Development of a portable grain mass flow sensor test rig[J].Computers and electronics in agriculture,2008,61(2):160-168. [10]Burks T F, Shearer S A, FultonJ P, et al.Effects of time-varying inflow rates on combine yield monitor accuracy[J].Applied Engineering in Agriculture,2004,20:269-276. [11]Schrock MD, Oard D L, Taylor R K, et al.A diaphragm impact sensor for measuring combine grain flow[J].Applied Engineering in Agriculture,1999,15(6):639-642. [12]邱白晶,姜国微,杨宁,等.水稻籽粒流对承载板冲击过程离散元分析[J].农业工程学报,2012,28(3):44-49. [13]魏新华,张进敏,但志敏,等.冲量式谷物流量传感器测产信号处理方法[J].农业工程学报,2014,30(15):222-228. [14]Shoji K,Matsumoto I,Kawamura T.Impact-by-impact sensing of grain flow on jidatsu combine[J].Engineering in Agriculture, Environment and Food,2011,4(1):1-6. [15]Hennens D, Baert J, Broos B, et al.Development of a flow model for the design of a momentum type beet mass flow sensor[J].Biosystems engineering,2003,85(4):425-436. [16]Reinke R, Dankowicz H, Phelan J, et al.A dynamic grain flow model for a mass flow yield sensor on a combine[J].Precision agriculture,2011,12(5):732-749. [17]田丹,薛定宇,陈大力.一种原始对偶去噪模型的参数选取与求解算法[J].信息与控制,2014(4):463-469. Grain Flow Model Based on Kinematic Analysis Wang He1,2,3, Hu Jingtao1, Gao Lei1 (1.Shenyang Institute of Automation Chinese Academy of Science, Shenyang 110016, China;2. University of Chinese Academy of Science, Beijing 100049, China;3. University of Science and Technology Liaoning, Anshan 114051, China) Abstract:Currently the grain flow models that were used for grain flow estimation were mainly empirical models.These models were difficult to meet the requirements of robust and versatility.A grain flow model was established based on kinematic analysis to accurately estimate mass flow. The model considered the external factors to grain flow measurement, such as the elevator rotation speed,the mechanical structure parameters,the relative positions parameters and grain characteristic parameters, and introduced relevant parameters that reflected changes of external factors. The relationship between the impact force and grain flow was nonlinear due to the variation of the external factors, a nonlinear least squares method was used to identify the grain characteristic parameters.An experimental platform was built to for the grain characteristic parameters and model validation.Three weighting sensors were mounted on the weighting bin in the experimental platform to calibrate grain flow sensor and verify the accuracy of grain flow sensor. A valve plate was inserted in the bottom of the feed bin of the experimental platform.The feed flow could be controlled by adjusting opening of the valve plate. Experimental results showed that the model can accurately describe the relationship between grain flow and impact, the maximum measurement error did not exceed 2.5%.The model was superior to the empirical models that were usually used, and is with versatility and robustness. Key words:grain flow model; kinematic analysis; impact 中图分类号:S24;TP29 文献标识码:A 文章编号:1003-188X(2016)11-0015-08 作者简介:王鹤(1981-),男,辽宁鞍山人,博士研究生,(E-mail) wanghe@sia.cn。通讯作者:胡静涛(1963-),男,沈阳人,研究员,博士生导师,(E-mail)hujingtao@sia.cn。 基金项目:国家高技术研究发展计划项目(2013AA040403) 收稿日期:2015-10-12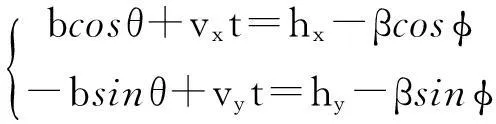
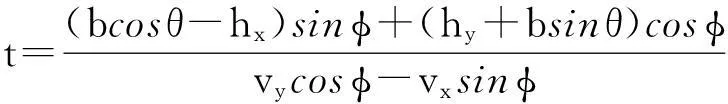
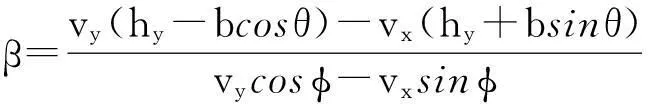
1.4 物碰撞传感器后的速度模型

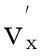



1.5 冲击力模型