水轮机叶片翼型参数化研究概述

朱尧华，袁寿其，张金凤，方玉建(江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013)

0 引 言

中国水电的发展从20世纪初的云南石龙坝电站到现在已经走过了100多年的历程。图1中展现了建国以后不同年代水电的装机容量和年发电量[1,2]。图1中标识了1960年我国自主设计的第一座水电站-新安江水电站；2004年随着公伯峡电站1号机组的投产，我国装机总量突破1亿kW，跃居为世界水电第一大国；如今水电的装机容量达到3.33亿kW。尤其近20年来，由于国家对大力发展水电事业的支持，特别是“西部大开发”国家战略，水电的发展可以说是处在蓬勃的发展时期，而且，这样的态势还将延续很长一段时期。

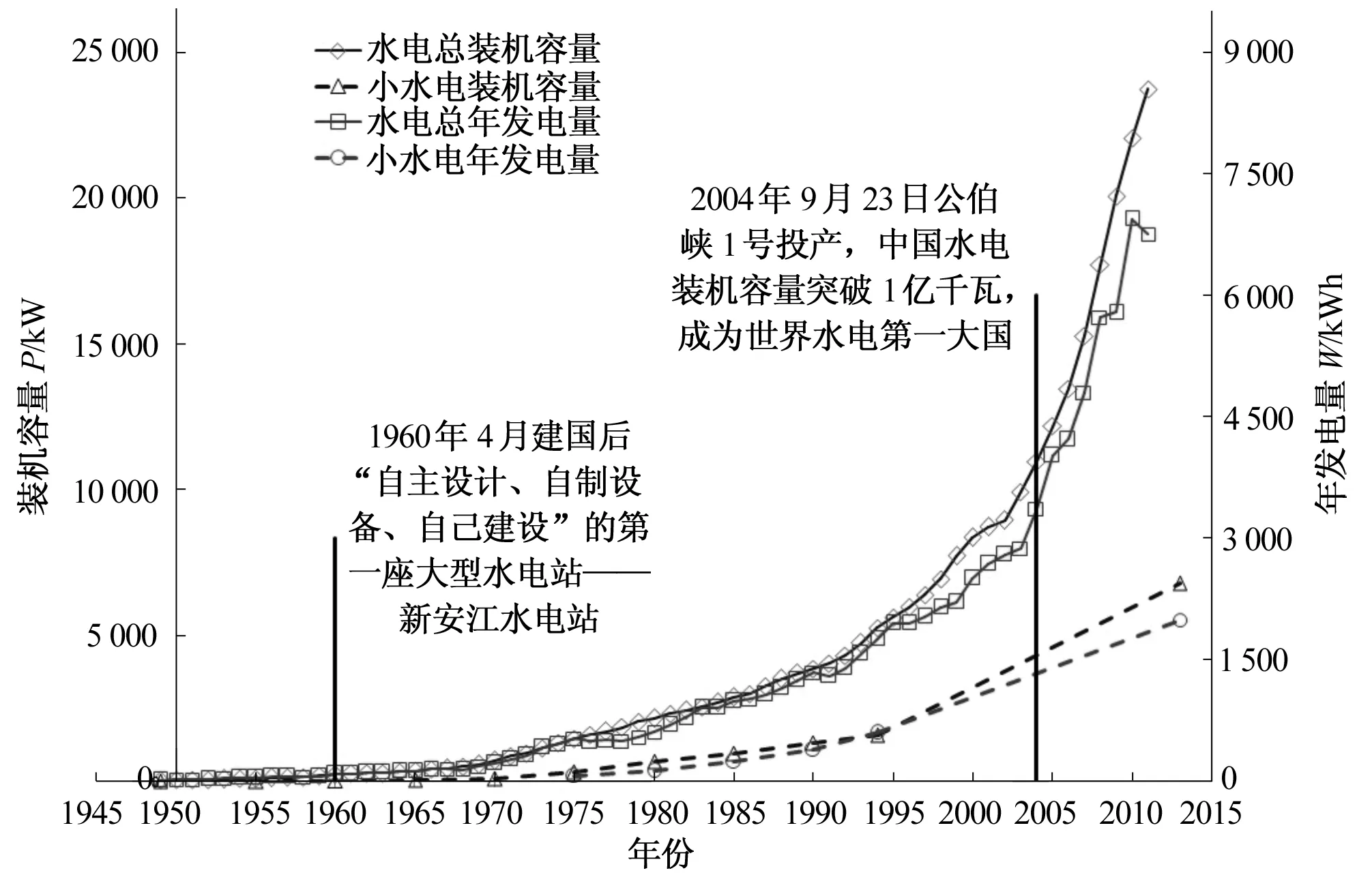
图1 我国水电发展历程图Fig.1 Hydropower development process in China

虽然我国水电事业发展迅速，但是水轮机设计开发的方法并不能匹配现如今水电的快速发展。传统的水力设计和开发是根据具体电站的参数和要求，每个项目都是从零开始做设计，然后进行大量的优化，包括设计和制作许多模型进行大量的模型试验，最终筛选出最优的水力模型。

随着经验的积攒以及一些优秀的水力模型的成功开发，尤其是计算机技术在几何造型、CFD计算、有限元计算方面的快速发展与成熟，并在流体机械中获得大量成功的应用，就出现了现代的水轮机的设计方法：根据项目具体参数要求和厂家已开发的水力模型进行初步水力分析，选择出适合作为进一步水力开发的基础模型，创建几何模型，采用计算流体模拟(CFD计算)和有限元分析(静态、动态应力和变形分析)联合进行优化。这个过程与传统的方法相比，它充分利用计算机技术实现优化的过程，取代了大量耗时投资大的模型制造和试验成本，具有很大的优势。即使如此，CFD模拟也不能代替模型试验，往往对于大型项目，还是需要开发设计1～3个模型进行试验筛选。

基于计算机的水力优化是从水力性能的角度去优化，包括效率、空化和压力脉力及其分布、动态应力及其分布和变形控制等方面的特性。但所有的优化计算，归根结底都是对转轮或模型几何形状的优化。

总之，具备一个高效的转轮叶片翼型和几何优化或参数化控制的方法，是实现这个水力和结构联合优化获得成功应用的核心。因此，对叶片翼型进行直接参数化的几何设计就有着重要的意义。

1 国内外发展现状

1.1 曲线的参数化思想

对于一般曲线的参数化设计理念，1988年M. Cardew-Hall等[3]提出完整的一般曲线参数化设计流程，即定义曲线→生成路径→计算曲线→创建模型→选取方案→反馈设计。国内在2002年金建国[4]等介绍了一般曲线参数化的各个模块及它们之间的内在联系。随后，金建国等[5]又提出了实现曲线参数化的6个基本要素，即曲线的分类，曲线尺寸的提取研究，曲线基本约束关系的归纳以及约束的语言文法表示，曲线、曲面的几何拓扑网状结构表示，约束的求解与几何推理和约束关系的满足方法。

对于具体的曲线参数化方法，2008年蔡江畔等[6]分别采用B样条曲线和参数3次样条曲线描述离心泵前后盖板、轴面流线和流线展开线，改变了传统手工设计方法，实现了计算机化。2011年张海军等[7]在飞艇外形设计过程中，采用了3种参数化方法：Bezier，B样条和NURBS。3种参数化方法在形式上基本相同，都包含基函数和控制点两部分；不同点是基函数的形式以及基函数中的变量取值范围不同。由于NURBS曲线多一组加权系数，增强了控制点对局部曲线形状的影响，故NURBS曲线拟合性能和效率都高于其他两种方法。

1.2 传统参数化方法应用于叶片翼型设计

水轮机叶片传统的设计方法主要有3种：升力法，保角变换法和奇点分布法[8]。相比较而言，奇点分布法[9]是应用相对广泛的一种参数化设计方法，它是用集中或者连续分布的涡、源、汇等奇点代替叶型。传统的参数化方法应用与叶片翼型设计优化中，主要是国内学者的一些研究。2009年薛正福等[10]在风力机适应性叶片中采用程序驱动法，利用了ANSYS APDL 参数化建模，通过分析模型的几何特点，确定了模型的主参数以及各尺寸间的数学关系。2010年朱国俊等[11]开发了基于奇点分布法和Bezier曲线参数造型方法的轴流式水轮机平面叶栅设计方法。先采用奇点分布法设计出翼型骨线并将骨线用Bezier曲线参数化，这样可以通过控制参数来变化骨线形状，然后把优秀翼型的厚度叠加到骨线上，这样就形成了通过控制参数的变化来变化叶栅翼型。2012年崔涛[12]用Bezier曲线参数化叶片翼型骨线，然后将导叶直接加到初始叶片进口前的流道上，保证了实际流动中转轮来流的真实条件。考虑叶片进出口边分别在轴向和周向上变化，多加了4个变量进行优化。2012年严敬等[13]将儒可夫斯基变换函数应用到轴流叶轮叶片的翼型设计中，以计算好的圆弧为骨线，采用被广泛应用的性能良好的791翼型加厚程序，最终得到流面完整翼型。2013年张为民等[14]运用NURBS进行翼型模板的定义，基于翼型模板的叶片参数化设计方法，根据叶片翼型弦长、安放角、叶片半径、翼型模板等参数进行叶片翼型数据的自动计算，求得各截面控制顶点的实际坐标；运用UG/open API 模块开发了叶片设计系统，实现了叶片设计的参数化。

1.3 整体参数化方法应用于叶片翼型设计

不同于传统的参数化设计叶片翼型的方法将参数化应用于翼型骨线等，近年来也有一些将参数化方法直接应用到叶片翼型的外形轮廓，然后，通过各类不同的求解方法(包括神经网络算法和遗传算法等)可以求得翼型轮廓的最优解。这样，可以采用有限数量的控制点坐标表征叶片翼型，对翼型的外形进行整体的控制，进而在今后的优化改进过程中仅需要改变控制点坐标实现改变叶片翼型的形状的作用。2003年M S Floater[15]提出并分析了一种无网格参数化的方法，这种方法基于评估曲线曲面的参数化方法，将一些无顺序点的样本重新建成一条曲线。 2007年I M Valakos等[16]指出差分进化算法用于优化的离心叶轮的背面几何形状，计算出的最大应力，以延长其超速极限。而背面的几何形状是使用Bezier曲线定义它的参数，并以此作为设计变量，用于现有优化程序。2010年闵新勇等[17]运用商业软件HyperWorks中HyperMorph模块的网格变形功能实现基于网格变形的翼型参数化。2010年Liang Y等[18]提出使用NURBS参数化方法设计多目标稳固翼型，并且对NASA SC0712翼型进行参数化设计，提升了翼型的气动性能。2011年Y Dong等[19]提出了一种简单而有效的逆设计方法，用于调整某些几何参数建立的叶片模具轮廓。2012年K Heinze等[20]提出了一种在设计过程中，采用概率方法来考虑压缩机叶片的几何偏差，根据气流的流线计算以下参数：前缘的轴向位置、前缘的切线位置、交错角、弦长、最大弯度及弦上位置、最大厚度及弦上位置、前缘厚度及弦上位置和后缘厚度及弦上位置。2012年李文全等[21]利用 Bezier 曲线对轴流泵叶片翼型坐标点进行曲线拟合，反求 Bezier 曲线控制点，从而可得各相应翼型曲线。2012年A Kharal等[22]指出基于Bezier-PARSEC 3434参数化方法和3种人工神经网络方法，使用15个参变量，采用基因算法对翼型进行造型，得到翼型的压力系数分布。2013年C B Allen等[23]提出悬停直升机旋翼的气动外形优化，利用可压缩CFD空气动力学模型，用作表面控制和变形的主要要素的外形参数化方法，链接到径向基函数全局插值，以提供主要要素运动的直接传递到设计表面和CFD体网格的变形，因此几何体的控制和体网格变形问题同时解决。2013年S. Walton等[24]比较了一些自由梯度算法，最终提出使用布谷鸟搜索算法对翼型和网格进行优化。2013年Q Wang等[25]提出使用B样条曲线对中等厚度的风机翼型后缘进行设计，并且使用改良的粒子群优化算法对翼型进行整体造型。2014年R Mukesh等[26]提出基于PARSEC参数化方法仅使用12个参数对航空翼型NACA2411进行设计，并且使用遗传算法对设计的翼型进行优化设计。2014年P D Vecchia等[27]在PARSEC 参数化翼型过程中以纳什平衡为目标采用基因算法优化翼型，并且认为CFD计算时应当采用StarCCM+ 和OpenFOAM软件。2014年Y V Pehlivanoglu[28]提出一种基于基因算法和神经网络的机翼翼型的逆设计方法，缩短了计算时间，并且比较了6种不同的算法，最后得出新的设计方法S12-GA最有效。2014年K Heinze等[29]提出翼型可以使用Voronoi图和Delaunay三角网参数化，并对水轮机叶片后缘骨线(图2)以及翼型(图3)进行参数化。2015年S Murugan[30]等在变弯度机翼的设计过程中，提出分级建模优化，采用多目标优化方法来满足机翼的几何外形和动力要求。

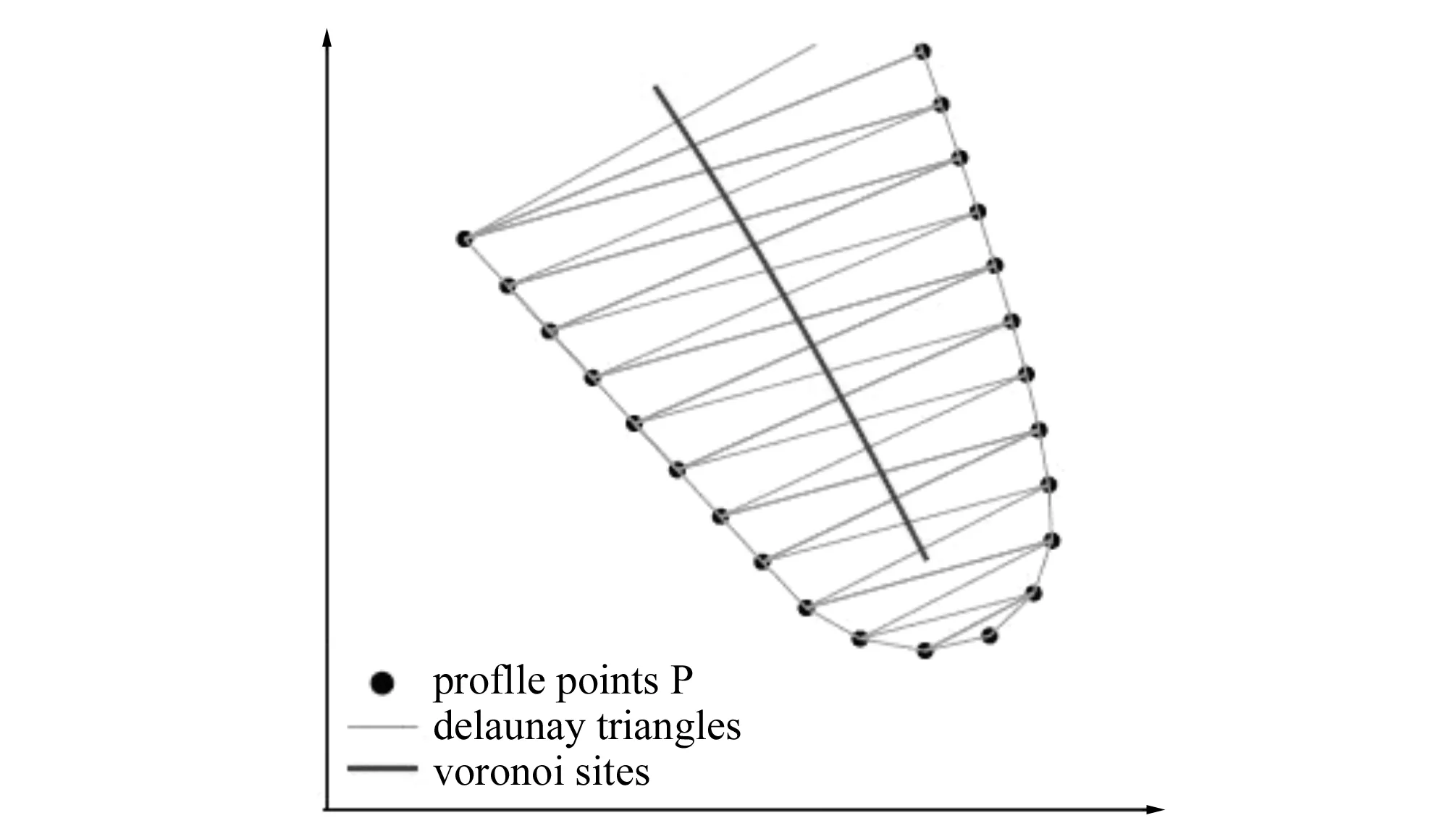
图2 Voronoi图(水轮机叶片后缘骨线)Fig.2 Voronoi graph (turbine blade trailing edge)

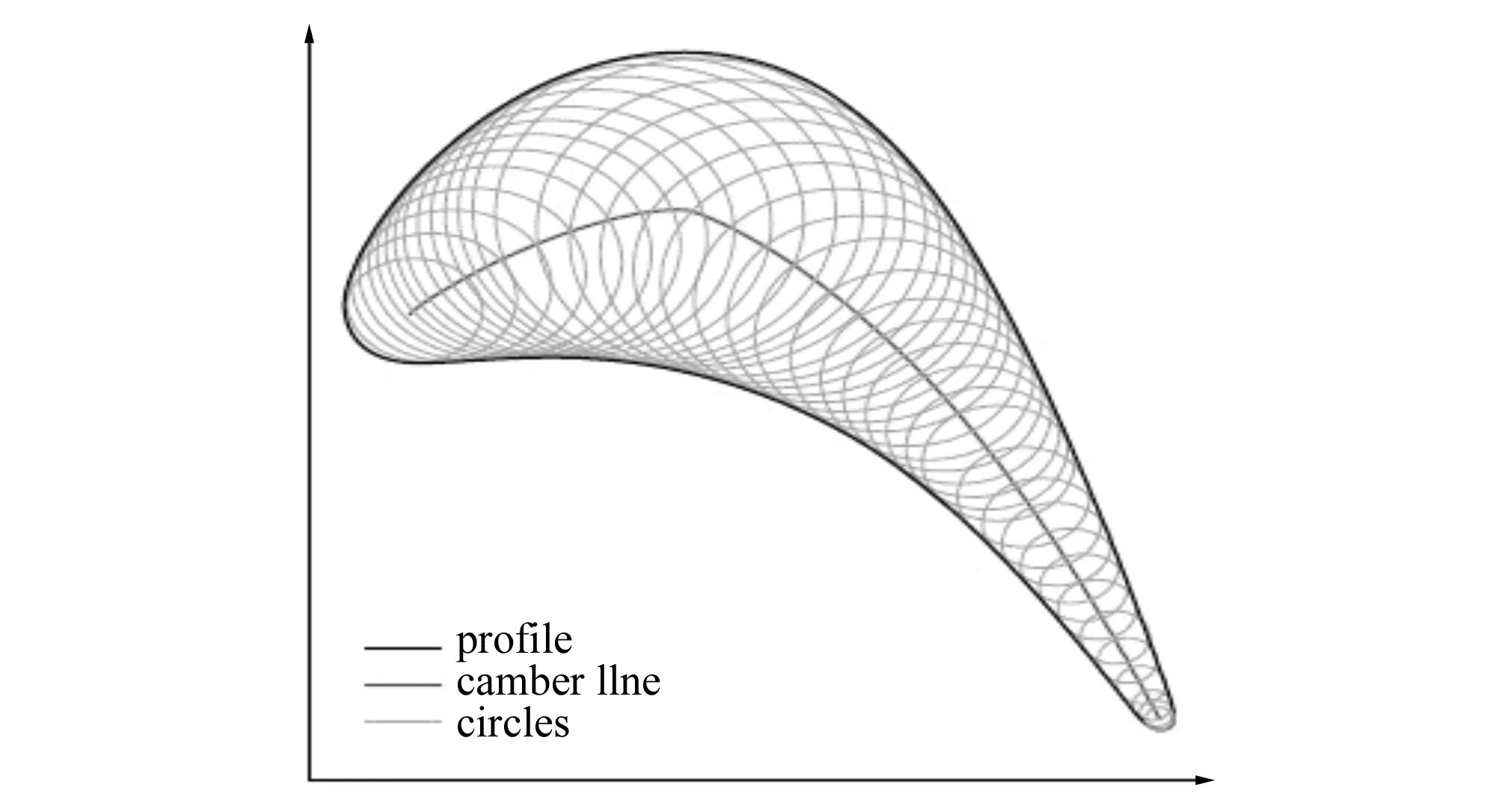
图3 Delaunay三角网参数化Fig.3 Delaunay parametric triangulation

因此，综上分析，可以得到以下结论。

(1)目前，随着计算几何学科的发展，对曲线参数化的研究已经非常成熟，尤其是在航空翼型方面出现了很多参数化设计优化方法。

(2)在水力机械领域，国内学者对曲线参数化进行了许多研究。从这些研究来看，主要是应用曲线参数化于具体的传统水力设计和优化，即将选取优秀的加厚程序应用到参数化的骨线流面上。但将曲线和曲面参数化直接应用于翼型和叶片的优化较少，其核心的问题是对翼型和叶片的参数化造型研究还不够深入和透彻。而由于整体参数化方法得到的结果在设计过程中已经进行初步的优化，并且由于参数数量有限，可以更容易通过改变参数进一步优化叶片翼型，所以国外学者在曲线参数化方面的研究更多，方法多种多样。

2 采用整体参数化方法应用于水轮机叶片设计

曲线参数化思想在航空翼型，特别是现有翼型谱中翼型的分析比较多，得到的多是翼型的气动性能，这是由于在气体中，雷诺数相对较低，流动相对稳定，升阻比较大[31]。其中使用的主要有几类重要的参数方法，Hicks-Henne型函数叠加法[32-34]和PARSEC几何参数法[35-37]等。

水轮机叶片传统的设计方法中应用最广泛的奇点分布法分析设计叶片时，一般认为翼型的厚度很小，可以用叶型骨线代替翼型。在选定翼型最大厚度和翼型厚度沿骨线变化规律后，就可以在各翼型骨线上作各计算截面的翼型的剖面图，即二维翼型图，随后，选定翼型转动轴线，并按此把各计算截面翼型组成转轮叶片。然而，奇点分布法在厚度较大的叶片的设计过程中，由于在设计过程中，叶型骨线代替翼型以及加厚程序的半经验性，其设计过程存在一定的偏差。因此，今后的研究应更多的将曲线参数化的方法直接应用到水轮机叶片翼型的设计，用有限数量的参数控制翼型的外形，并且在确定控制点坐标的过程中采用优化算法选取最佳的解，得到的叶片翼型相对较好，再者，选用参数控制叶片翼型可以在优化过程中更加简便的通过控制点坐标的变换实现几何上的改变，达到优化的作用。

然而一般在水轮机叶片的设计过程中，由于水力性能的要求，很少采用单一翼型库中的翼型，而是很多未知翼型的组合。因此分析水轮机叶片的过程中，需要从叶片中截取翼型进行参数化的分析。除了这些，在翼型的整体参数化造型中，还需要着重注意以下几个问题。

2.1 控制点的选取

选取合适的控制点[38]是该方法的第一步，也是该方法最重要的一个环节。控制点的选取直接关系到它的轮廓。一般参数化过程中，控制点坐标由翼型的特征变量(例如最大厚度及位置、最大隆起高度及位置等)来表征。当然，不同的方法得到的控制点也是不一样的，但是，所有方法的目的相同，都是为了得到拟合度更高的曲线，图4为由Bezier曲线参数化的某水轮机叶片翼型。

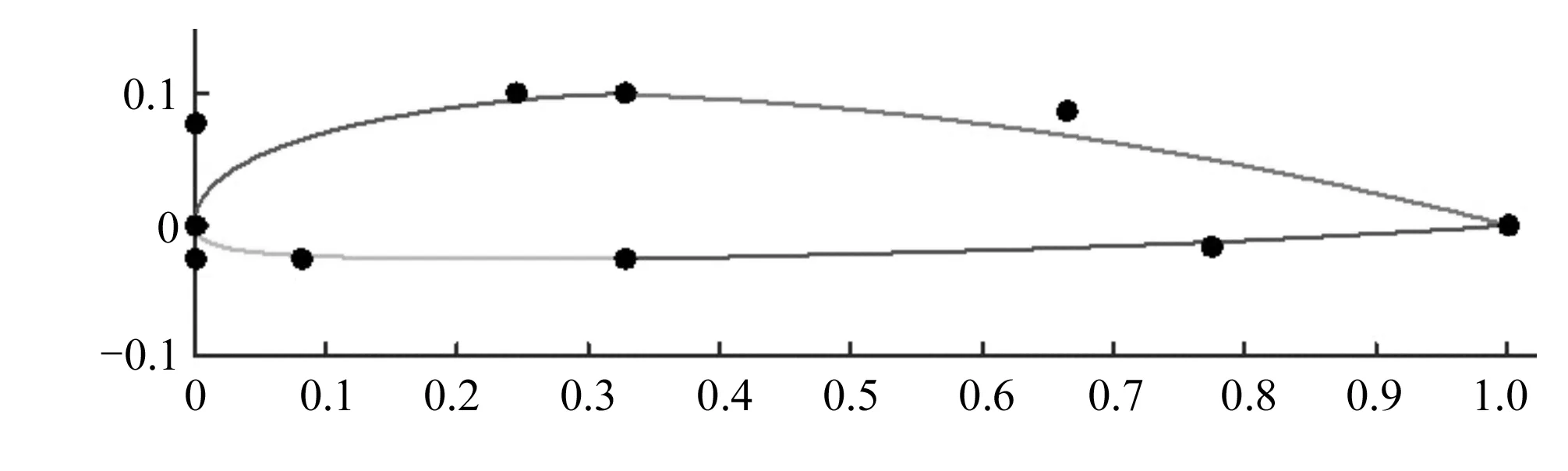
图4 Bezier曲线参数化的某水轮机叶片翼型Fig.4 One Kaplan turbine airfoil parameterized by Bezier curve

2.2 方法的通用性

选取了一种参数化的方法，可能对这类翼型适用，然而，对于另外的不同形状的翼型可能出现拟合度不高的情况，造成误差较大，因此选取通用的翼型参数化方法，即通用的控制点，是该方法普遍适用的关键所在。一般而言，对于宽翼型拟合度较高的方法，而对于较窄的翼型拟合度较低。所以，选取通用的参数化方法是得到简单易行的曲线轮廓的关键。

2.3 水力特性的比较

一般航空翼型的好坏由其气动性能(如升阻比等)决定。而水轮机翼型不仅需要考虑升阻比等因素，更重要的是翼型生成的叶片的水力特性(如空化性能等)。一般情况下，参数化的方法虽然可以得到外形上与原翼型相似的轮廓，但是其水力性能与原翼型相比，还是会存在一定的偏差。由于水轮机叶片翼型最主要的还是其水力性能[39]，所以参数化的关键在于寻找简单便捷的参数化方法的同时，保持或者优化翼型的水力性能。

3 结 语

采用曲线参数化的方法来设计叶片翼型，较传统的设计方法，具有操作简单，方便等特点，国内外对其的研究在航空领域已经比较成熟，但是在水力机械方面，参数化的思想还是相对落后，尤其在国内，想法思路已经出现，但是还是很多局限在以骨线为参数化的对象，通过加厚程序实现参数化建模，而真正把翼型轮廓作为参数化的对象目前还比较少。由于参数化的方法可以简单地改变翼型叶片的形状从而达到优化其水力性能的作用[40]，今后对叶片翼型结合参数化的研究，当然同时也要注意其与水轮机叶片相结合的问题，这样才能为水轮机叶片优化设计的发展开拓新的方法。

□

[1] 邴凤山. 中国水力发电年鉴(第16卷)[R]. 北京：中国电力出版社, 2011:17-18.

[2] 水利部农村电气化研究所.小水电现状[EB/OL].http:∥www.hrcshp.org/aboutshp/aboutshp.asp?docId=05.2013-12-17.

[3] Cardew-Hall M, Cosmas J, Ristic M. Automated proof inspection of turbine blades[J]. The International Journal of Advanced Manufacturing Technology, 1988,3(2): 67-88.

[4] 金建国, 周明华, 王明怡,等. 曲线参数化模型研究[J]. 浙江大学学报(工学版), 2002,36(1):597-597.

[5] 金建国, 包 晔, 缪永伟. 曲线参数化技术研究与分析[J]. 浙江工业大学学报, 2003,31(5):580-585.

[6] 蔡江畔, 李 春, 李沈坚. 参数曲线在水泵叶轮设计中的应用[J]. 上海理工大学学报, 2008,30(4):311-314.

[7] 张海军, 郭雪岩, 戴 韧. 飞艇外型设计中曲线参数化方法的比较[J]. 力学季刊, 2012,32(4):634-639.

[8] 曹 鲲, 姚志民. 水轮机原理及水力设计[M]. 清华大学出版社, 1991.

[9] 张礼达, 陈维森. 轴流式转轮叶片奇点分布法 CAD 软件设计与研究[J]. 水动力学研究与进展: A 辑, 1998,13(4):397-405.

[10] 薛正福. 风力机适应性叶片的参数化建模与有限元分析[D]. 呼和浩特：内蒙古工业大学, 2009.

[11] 朱国俊, 罗兴锜, 郭鹏程, 等. 基于组合优化方法的平面叶栅优化设计[J]. 大电机技术, 2010,(1):50-53.

[12] 崔 涛. 基于遗传算法的轴流式水轮机叶片优化设计[J]. 现代制造, 2012,(33):122-123.

[13] 严 敬, 王 桃, 肖国华, 等. 基于儒可夫斯基变换的轴流叶片翼型设计[J]. 排灌机械工程学报, 2012,30(3):265-269.

[14] 张为民, 郝小忠, 何 磊. 基于 NURBS 的涡轮叶片参数化设计[J]. 机械设计与制造工程, 2013,42(8):23-26.

[15] Floater M S. Analysis of curve reconstruction by meshless parameterization[J]. Numerical Algorithms, 2003,32(1):87-98.

[16] Valakos I M, Ntipteni M S, Nikolos I K. Structural optimization of a centrifugal impeller using differential evolution in CATIATMenvironment[J]. Operational Research, 2007,7(2):185-211.

[17] 闵新勇. 风力机翼型的气动性能模拟与优化设计[D]. 上海：上海交通大学, 2010.

[18] Liang Y, Cheng X Q, Li Z N, et al. Multi-objective robust airfoil optimization based on non-uniform rational B-spline (NURBS) representation[J]. Science China Technological Sciences, 2010,53(10):2 708-2 717.

[19] Dong Y, Zhang D, Bu K, et al. Geometric parameter-based optimization of the die profile for the investment casting of aerofoil-shaped turbine blades[J]. The International Journal of Advanced Manufacturing Technology, 2011,57(9-12):1 245-1 258.

[20] Heinze K, Schrape S, Voigt M, et al. Probabilistic endurance level analyses of compressor blades[J]. CEAS Aeronautical Journal, 2012,3(1):55-65.

[21] 李文全. 轴流泵叶片动力特性预测模型研究[D]. 西华大学, 2012.

[22] Derksen R W, Rogalsky T. Bezier-PARSEC: An optimized aerofoil parameterization for design[J]. Advances in engineering software, 2010,41(7):923-930.

[23] Allen C B, Rendall T C S. CFD-based optimization of hovering rotors using radial basis functions for shape parameterization and mesh deformation[J]. Optimization and Engineering, 2013,14(1):97-118.

[24] Walton S, Hassan O, Morgan K. Selected engineering applications of gradient free optimisation using cuckoo search and proper orthogonal decomposition[J]. Archives of Computational Methods in Engineering, 2013,20(2):123-154.

[25] Wang Q, Chen J, Pang X, et al. A new direct design method for the medium thickness wind turbine airfoil [J]. Journal of Fluids & Structures, 2013,43(7):287-301.

[26] Mukesh R, Lingadurai K, Selvakumar U. Airfoil shape optimization using non-traditional optimization technique and its validation[J]. Journal of King Saud University-Engineering Sciences, 2014,26(2):191-197.

[27] Vecchia P D, Daniele E, D`Amato E. An airfoil shape optimization technique coupling PARSEC parameterization and evolutionary algorithm [J]. Aerospace Science & Technology, 2013,32(1):103-110.

[28] Pehlivanoglu Y V. Direct and indirect design prediction in genetic algorithm for inverse design problems [J]. Applied Soft Computing, 2014,24:781-793.

[29] Heinze K, Meyer M, Scharfenstein J, et al. A parametric model for probabilistic analysis of turbine blades considering real geometric effects[J]. CEAS Aeronautical Journal, 2014,5(1):41-51.

[30] Murugan S, Woods B K S, Friswell M I. Hierarchical modeling and optimization of camber morphing airfoil [J]. Aerospace Science & Technology, 2015,59(2):31-38.

[31] 李德顺, 李仁年, 杨从新,等. 雷诺数对风力机专用翼型气动性能影响的研究[J]. 流体机械, 2009,37(12):31-34.

[32] Hicks R M, Henne P A. Wing design by numerical optimization[J]. Journal of Aircraft, 1978,15(7):407-412.

[33] Wu H Y, Yang S, Liu F, et al. Comparison of three geometric representations of airfoils for aerodynamic optimization[C]∥16th AIAA Computational Fluid Dynamics Conference. 2003.

[34] 左林玄, 王晋军. 低雷诺数翼型的优化设计[J]. 兵工学报, 2009,30(8):1 073-1 077.

[35] 尹 强, 高正红. 外形参数化方法对气动优化过程的影响[J]. 科学技术与工程, 2012,20(14):3 394-3 398.

[36] 廖炎平, 刘 莉, 龙 腾. 几种翼型参数化方法研究[J]. 弹箭与制导学报, 2011,31(3):160-164.

[37] Sobieczky H. Parametric airfoils and wings[J].Notes on Numerical Fluid Mechanics,1998:71-88.

[38] 孙 勤, 张俊彦, 邹汝红. 三种翼型参数化方法的研究[J]. 湘潭大学自然科学学报, 2013,35(3):34-39.

[39] 刘德民, 程 宦, 袁凌丽. 潮流能水轮机水力特性研究[J]. 东方电机, 2013,41(6):9-12.

[40] 陈红勋, 霍聪聪, 刘文梅. 基于 CFD 的分段翼型控制研究[J]. 排灌机械工程学报, 2012,30(5):513-516.