基于投影寻踪聚类模型的水务系统评价——以郑州市为例

周振民，管 财，范 秀，李延峰(.华北水利水电大学，郑州 4500；.新乡市大功引黄工程管理处，河南 新乡 453300)

0 引 言

众所周知，21世纪被称为“水的世纪”，水危机已成为继能源危机之后，人类面临的又一难题，水资源匮乏已成为关系到经济可持续发展、世界贫困人口生存乃至世界和平与安全的重大问题。应对水危机、解决水问题，关键在于做好水务系统的管理工作，研究水务系统、掌握水务系统发展现状以及存在的问题、制定科学合理的发展战略，从而实现人、水、经济社会和谐发展的目的。城市水务系统包括水资源环境、水源、供水、用水、排水、水处理与回用，以及相关的资源管理和产业管理，其主要任务是为城市水资源开发、利用、配置、节约和保护提供科学的管理和服务[1]。目前，有关水务系统评价的方法主要有主成分分析法、熵值法[2]、层次分析法等，这些方法都存在一些问题，比如主成分分析法要求前几个主成分的累计贡献率必须达到一个较高的水平，层次分析法指标选取受人为干扰性大等，而本文采用了投影寻踪聚类模型分析法，可以克服上述两个方法的弊端，从而更科学地构建水务系统综合评价模型指标体系，建立投影寻踪目标函数，从而用遗传算法求得最优解，进而得到郑州市水务系统评价等级为Ⅱ级。

1 投影寻踪模型理论基础

1.1 投影寻踪模型简介

投影寻踪方法最早由美国科学家Kruscal 提出并使用，他把一组高维数据投影到低维数据空间，发现了数据的聚类结构，进而解决了化石分类问题。Tukey和Friedman教授在1974年发现了一种把局部的凝聚程度和整体散度结合的新指标，用于聚类模型分析，并首次提出了投影寻踪的概念，并于1976年编制了计算机图像系统。

在此之后，投影寻踪模型计算方法在理论和应用领域取得了长足进展，Friedman等学者于1981年提出了投影寻踪分类模型、投影寻踪回归模型和投影寻踪密度函数估计。1985年Huber对前人的成果进行了归纳和总结，发表了关于投影寻踪的综合性论文，并初步建立了投影寻踪模型在统计学中的独立运用体系。至此投影寻踪模型开始在实践中的大规模应用。目前投影寻踪模型主要用于以下3个方面：投影寻踪回归模型、投影寻踪聚类分析和投影寻踪学习网络。

投影寻踪聚类方法主要用于将模型中的高维数据投影到低维空间中，即1～3维的可视空间，然后通过数学计算，优化反映数据聚类程度的一个指标，得到若干个投影方向，在这多个投影方向中找到最优的投影方向。在这个投影方向下，投影到低维空间的点能够最直接地反映高维空间散点数据的特征，这样我们就可以通过研究低维数据结构特征，学习和掌握高维数据空间的特征。所以说投影寻踪模型方法的关键就是找到最佳投影方向，这正是该模型研究者们一直研究的重点。本文采用的是一种全局优化方法——遗传算法(Genetic Algorithm ，GA)来计算最佳投影方向，该方法不是把优化区域划分为若干个小区域，在小区域上求最优解，而是根据目标函数反映在低维空间结构上的特征，在整个优化域内求最优解，所以不会错失任何最优解[3]。

1.2 投影寻踪模型求解过程

1.2.1评价指标归一化处理

由于评价指标种类多，而各指标的量纲又存在差别。因此，为了消除各指标的量纲影响，并统一各指标取值的变化区间，在建立模型之前首先需要将指标分成越大越优型和越小越优型两种类型，对指标数据进行归一化处理。归一化处理的方法不同，对投影寻踪模型有一定的影响，本文采用常规的处理方法加以处理[4]。

各指标值用样本{x*(i,j)|i=1,2,…,n,j=1,2,…m}表示，其中x*(i,j)为第i个样本第j个指标值，n、m分别为样本的个数(样本容量)和指标的数目。为消除量纲和指标值的变化范围对结果的影响，应用下式进行极值归一化处理：

步骤1：对于越大越优的指标

(1)

对于越小越优的指标

(2)

式中：xmax(j)、xmin(j)分别为第j个指标值的最大值和最小值；x(i,j)为指标特征值归一化的序列。

1.2.2线性投影

投影寻踪中投影的目的是寻求能够最大限度地反映样本数据结构特征、最能够充分挖掘样本数据信息的最优观察角度，即最佳投影方向。其实质就是通过投影的方法、把高维数据所反映的信息投影到一维空间里，这样处理的结果非常形象、直观，也便于使用常规的数学方法对高维数据进行处理和分析[5]。

1.2.3构造投影指标函数

构造投影指标函数F是投影寻踪计算过程中的关键步骤。水务系统评价主要是对样本进行级别判断，通常采用分类指标来构造投影指标函数，即投影特征值在低维空间散布的类间距离与类内密度同时达到最大值。

投影寻踪聚类模型方法就是把p维数据{x(i,j)|i=1,2,…,p}综合成以a={a(1),a(2),a(3),…,a(p)}为投影方向的一维投影值z(i)。

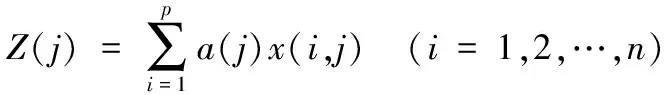
(3)

式中：a(j)为投影向量。

根据投影函数的特性，要求投影值z(i)的散布特征向量应为：局部投影点尽可能密集，尽可能凝聚成若干个点团，但整体上投影点团之间尽可能散开。因此，投影指标函数可以表达成

F(a)=SzDz

(4)

式中：Sz为投影值z(i)的标准差；Dz为投影值z(i)的局部密度。即

(6)

式中：E(z)为序列{z(i)|i=1,2,…,n}的平均值；R为局部密度的窗口半径(密度窗宽)，其值可以根据试验来确定；r(i,j)表示样本之间的距离，r(i,j)=|z(i)-z(j)|；u(t)为一单位阶跃函数，当t≥0时，其值为1，当t<0时，其函数值为0。

1.2.4优化投影指标函数

对于给定指标的样本集，投影指标函数值只随投影方向的变化而改变。不同的投影方向必然反映出不同的数据结构特征，其中，可能最大限度暴露高维数据特征结构的投影方向就是最佳的投影方向。相关研究表明，当投影指标函数F=Fmax(a)取得最大值时，就得到投影指标函数F(a)的最佳投影方向。即:

最大化目标函数

maxF(a)=ZzDz

(7)

约束条件

(8)

这是一个以{a(j)|j=1,2,…,p}为优化变量的复杂非线性优化问题。利用遗传算法与MATLAB工具箱中的直接搜索工具箱求最优解，用MATLAB代码编写适应度函数，在MATLAB中以M文件的形式存储适应度函数，方便直接搜索工具箱的调用，在MATLAB中运行所编写的投影寻踪模型程序，求得该水务系统评价模型的最优解。

1.2.5用遗传算法求最优投影方向

在投影寻踪模型中，最关键的一个环节就是寻求该模型的最佳投影方向，本文采用的是基于生物进化理论的全局优化方法——遗传算法。遗传算法最早由美国Holland教授于20世纪60年代提出，经过几十年的发展，Goldberg于80年代对该方法进行了系统的归纳总结，形成了遗传算法的基本框架，其主要步骤包括：选择(Selection)、交叉(Crossover)和变异(Mutation)[6]。然后模拟生物界对变异的数据进行筛选，找到初次优化的变异数据，如此进行多代的交叉、变异和重组，找到最优解。该方法能够避免诸多优化方法的缺点，使投影目标函数能够在可行域内实现最优，该方法是一种有效确定最佳投影向量的算法。

2 基于投影寻踪模型理论的郑州市水务系统评价

2.1 概 述

郑州市北临万里黄河，西靠中岳嵩山，东南接黄淮海大平原，属北温带季风气候，年平均气温14.3 ℃，平均降水量640.9 mm。境内大小河流35条，分属于黄河水系和淮河水系，其中流经郑州段的黄河长150.4 km，，郑州市土地面积7 446 km2，市区面积1 010.3 km2，常驻人口866万人，人均GDP 47 608元/人，建城区面积343 km2。

经过多年的不懈努力，郑州市水务建设取得了很大的成绩，基本满足了城市供水的需求，尤其是水务一体化改革之后，水务局履行了水务一体化管理职责。水务系统与日常生活息息相关，对于社会各个子系统的正常运转起到积极的推动作用，水务系统的综合评价是对于我们现阶段水务系统建设的一次系统研究分析，并且对于以后的城市水务系统的发展方向有一定的指引作用[7]。水务工程是保障城市安全有序发展的重要基础设施，城市水务工程体系的建设水平要和当地的社会经济发展速度相适应，要根据现状条件下的工程建设和运行情况，分析城市防洪排涝、供水、节水、污水收集处理、污水回用、水生态环境建设等工作对社会经济发展的影响。

2.2 研究技术路线

本文采用如下技术路线进行了水务系统评价研究。首先，明确本论文研究的目的，结合研究目标，构建水务系统评价指标体系，然后进行郑州市水务系统的数据收集与处理，进而选择投影寻踪聚类模型评价方法进行评价，最后得综合评价。

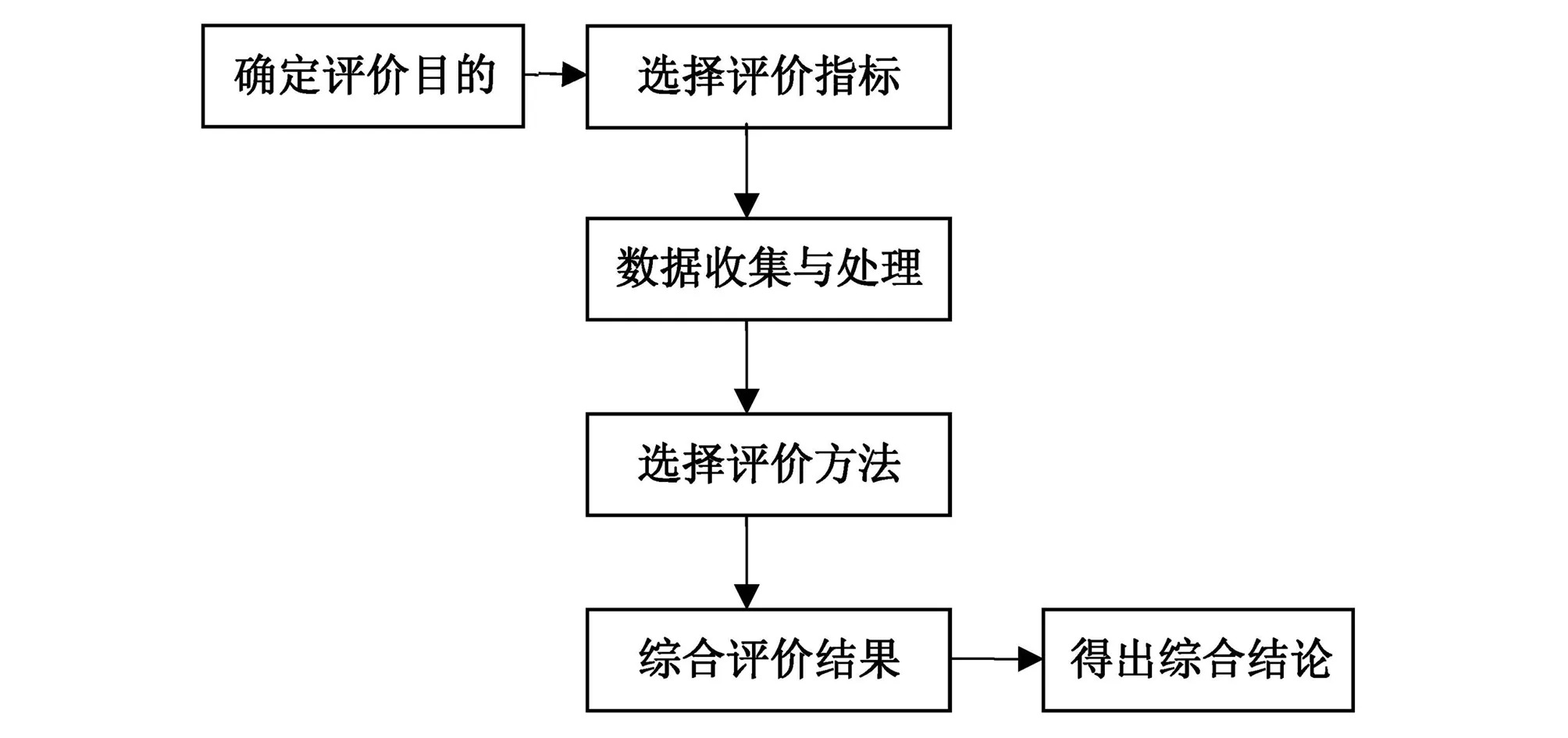
图1 研究技术路线图Fig.1 The skechmap of research

2.3 投影寻踪评价模型的建立

统筹考虑水务系统的各个子系统，选取各子系统的代表性指标，进而构建合理的水务系统指标评价体系。构建水务系统评价指标要遵循以下原则：

(1)综合性。指标选择时，要从城市的特点及水环境要素等方面综合考虑，不要求对城市水务的各个要素进行细致的分析。

(2)代表性和导向性。选取的指标要能反映城市水务系统的综合质量状况，即所选指标要能反映城市水体的水质情况、防洪情况、供水情况、再生水水利用情况，以及城市水务系统的变化趋势等，为城市水务的管理者提供决策的依据。

(3)可操作性。指标数据应容易获得，并且真实可靠，指标须有一定切实可行的量化方法可以利用，指标体系的指标条目数量应当适中，过多在评价中难以实施，过于简化又不能说明问题，更无法得到正确的评价结果。

2.4 评价指标构建

城市水务系统是城市涉水事务的各个子系统的综合，各个子系统之间既相互联系又相互制约。城市水务系统是以工程建设为主的传统工程水利逐步向以资源优化配置和环境生态平衡为主要目标的资源水利转变的结果[8]。从城市水务的系统功能上来说，城市水务系统包括水资源环境、水源、供水、用水、排水、水处理与回用，以及水务系统管理。其主要任务是为城市水资源开发、利用、治理、科学配置、节约和保护提供核心的技术支撑[9]。

结合城市水务的系统特征，从技术的层面划分为9个子系统，城市防洪系统、城市节水系统、城市供水系统、城市排水系统、城市中水回用系统、城市污水系统、城市水生态环境系统、水务管理系统及社会环境系统[10-15]。

运用投影寻踪模型，对样本数据进行处理，根据水务系统的评价等级分类，将水务系统评价等级分为Ⅰ、Ⅱ、Ⅲ、Ⅳ 4个等级，依次为优良、良好、及格和差。

在MATLAB中优化该目标函数，计算得到如下结果，见表2。

2.5 评价结果分析

计算最佳投影方向向量a*=(-0.010 17，0.046 171，0.498 364，0.349 984，0.011 902，0.152 378，0.136 069，0.186 38，0.043 024，0.306 349，0.194 764，0.190 925，0.624 06)，Ⅰ、Ⅱ、Ⅲ、Ⅳ级的各标准样本对应的投影特征值Z*j分别为：2.730 198 947，1.698 662 714，0.861 438 824，0。即水务系统评价等级标准样本的投影特征值向量z=(2.730 198 947，1.698 662 714，0.861 438 824，0)。

将最佳投影方向向量值和各投影方向特征值代入式(3)得到郑州市水务系统评价模型的投影特征值Z*j=1.819 078。绘制水务系统等级值Z*j与投影特征值之间的关系图，并根据曲线图建立水务系统评价等级判别函数y=P(z)，即投影寻踪等级评价模型。

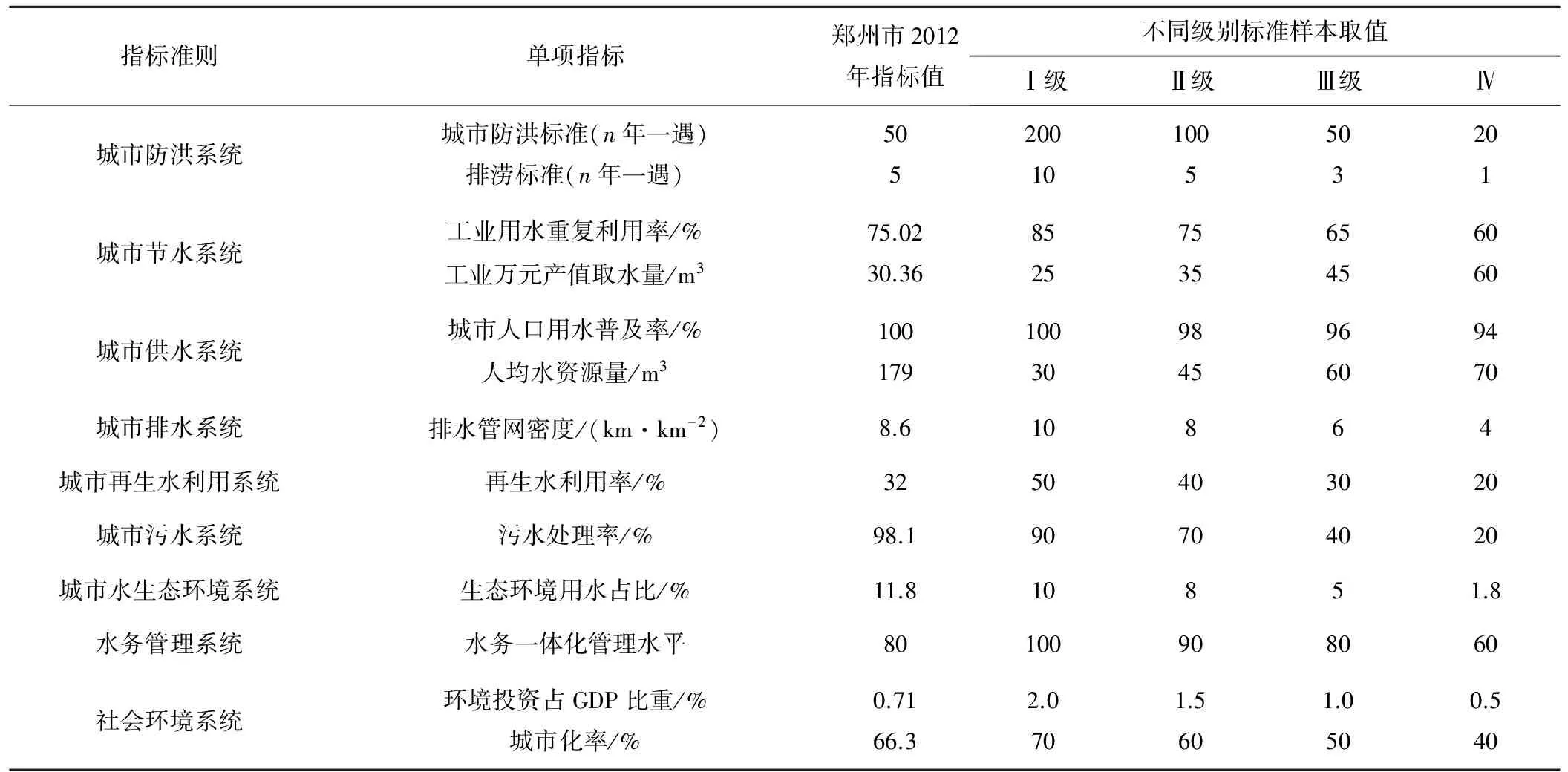
表1 郑州市水务系统评价指标及单项指标标准Tab.1 The evaluation indexes of water system and single standard index in Zhengzhou

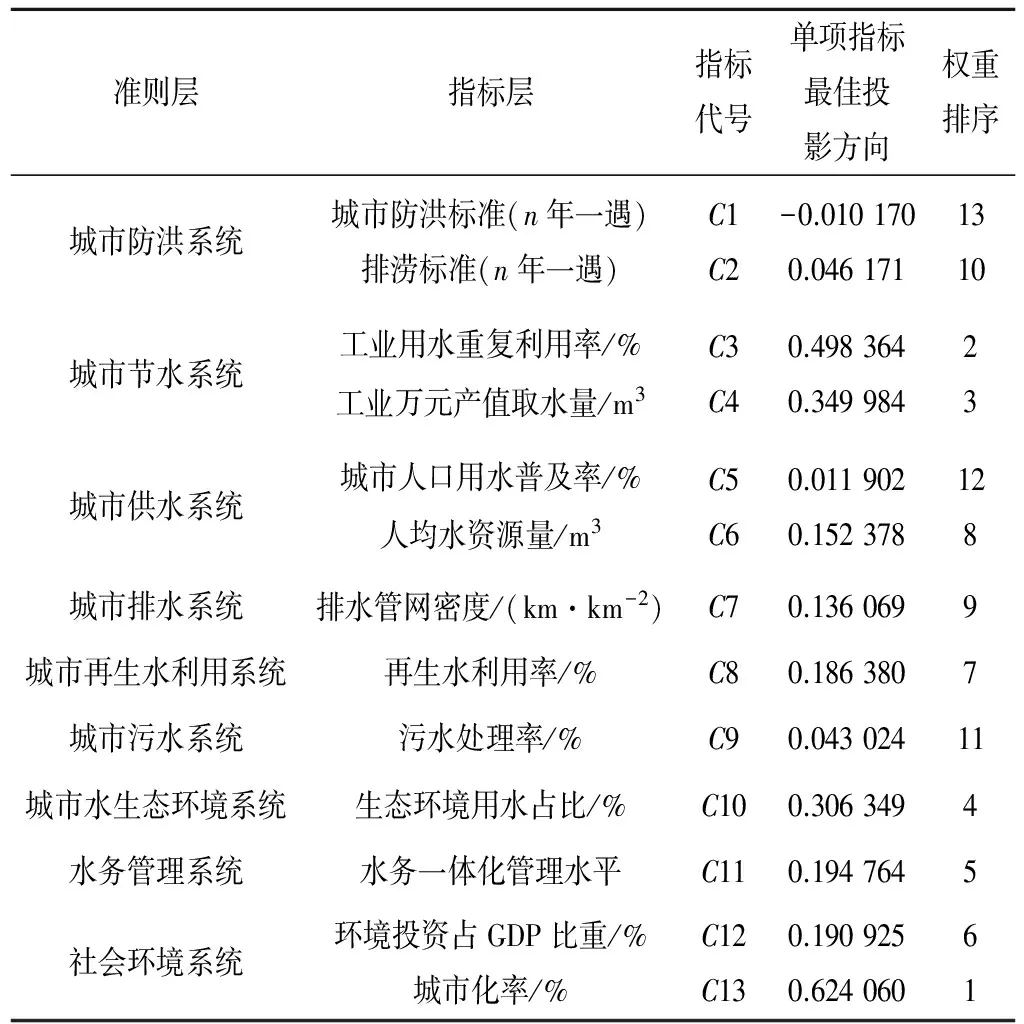
表2 投影寻踪模型单项指标最佳投影方向分量Tab.2 The single index best projection direction component for projection pursuit model

首先绘制各等级标准样本对应的投影特征值Z*j与水资源承载能力间的关系图(图2)，然后根据关系图变化趋势建立投影寻踪等级评价函数y=P(z)。

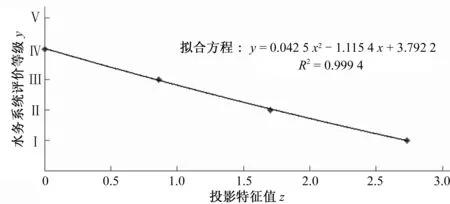
图2 投影特征值与水务评价等级拟合图Fig.2 Relationship between eigenvalue and the evaluation of water systems

从表3可以看出，投影特征值与拟合评价模型等级平均绝对误差为8.35×10-5，平均相对误差为6.298 7%。显然，该模型误差较小，精确度高，因此该模型可用来评价郑州市的水务系统现状。

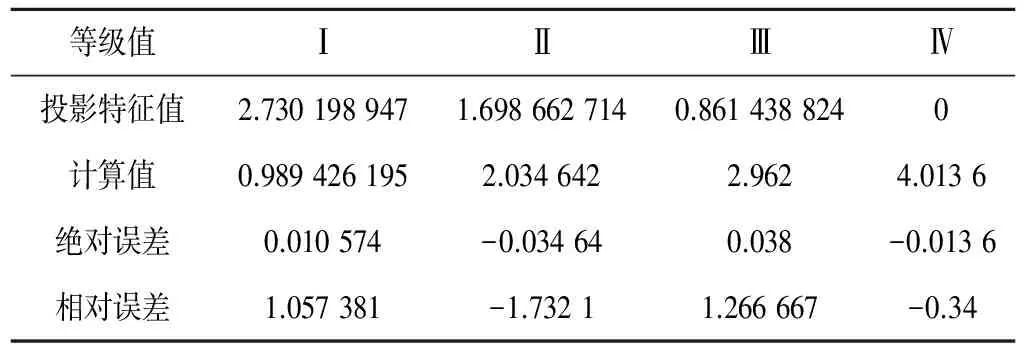
表3 投影寻踪模型评价结果误差分析Tab.3 The error analysis of the projection pursuit grad evaluation model

将郑州市水务系统评价投影特征值代入拟合等级函数y=0.042 5x2-1.115 4x+ 3.792 2得到y=1.184 051 1，该值接近评价等级的第Ⅱ级，因此郑州市的水务系统等级为Ⅱ级。当前水务系统处于良好状态。

3 结 语

城市水务系统是一个复杂的大系统，包含一个区域的所有涉水事务，并在不断地发展和完善，因此，对于水务系统的研究仍需不断的深入。本文在充分考虑郑州市水务系统影响因素的基础上，以郑州市城市防洪系统、城市节水系统、城市供水系统、城市排水系统、城市再生水利用系统、城市污水系统、城市水生态环境系统、水务管理系统、社会系统等9个系统为评价基础，全面系统的分析当前郑州市水务系统建设运行状况，取得了如下结论。

(1)采用系统分析模型，将水务系统看做一个完整的、开放的巨系统加以研究。通过研究水务系统的各个子系统，并加以凝练和总结，提出了一个有代表性的评价指标来概括该子系统，加深了对水务系统内涵的认识，为科学的分析城市水务系统的组成提供了一定的依据。

(2)结合郑州市水务系统的具体情况，筛选了13项具体评价指标，包括城市防洪标准、排涝标准、工业用水重复利用率、工业万元产值取水量、城市人口用水普及率、人均水资源量、排水管网密度、再生水利用率、污水处理率、生态环境用水占比、水务一体化管理水平、环境投资占GDP比重、城市化率。这些指标能够基本概括郑州市的水务发展核心要素。

(3)在建立水务系统评价指标体系的基础上，首次将投影寻踪模型应用于水务系统的综合评价，并运用遗传算法对目标函数进行优化，最后得到具体的评价结果。结果显示，目前郑州市社会环境系统、城市节水系统、城市水环境系统建设方面存在不足，需要作为当前水务系统建设的重点内容。本次系统评价为政府相关决策部门提供了一种可参考的依据，有利于对目前水务系统建设的薄弱环节进行改进，进而使郑州市的水务系统建设得到全面的发展。

□

[1] 谢京.城市水务大系统分析与管理创新研究[D].天津：天津大学,2007.

[2] 方国华,程发顺,黄显峰,等. 基于熵值法的徐州市水利水务现代化评价研究[J]. 水资源与水工程学报,2014,(6):34-38.

[3] 付 强. 投影寻踪模型及其在水文水资源系统分析中的应用[J]. 黑龙江水专学报,2008,(4):80-85.

[4] 马 峰,王 千,蔺文静,等. 基于指标体系投影寻踪模型的水资源承载力评价——以石家庄为例[J]. 南水北调与水利科技,2012,03:62-66.

[5] 万中英,廖海波,王明文. 遗传-粒子群的投影寻踪模型[J]. 计算机工程与应用,2010,20:210-212,240.

[6] 甄伟平.投影寻踪模型在生态系统评价中的应用[D]. 兰州：兰州大学，2011.

[7] 张海涛,谢新民,杨丽丽. 水利现代化评价指标体系与评价方法研究[J]. 中国水利水电科学研究院学报,2010,(2):107-113.

[8] 生春新. 泰州水生态工程可持续发展研究[J]. 江西建材,2014,20:118.

[9] 吴季松,石玉波,李砚阁.水务知识读本[M].北京:中国水利水电出版社,2003.

[10] 程晓冰. 我国水务管理20年回顾与展望[J]. 水资源管理.2015,(11).

[11] 刘大根. 北京市“十三五”时期水务发展规划编制的思考与建议[J]. 中国水利,2015,(11):18-20.

[12] 邵益生. 城市水系统控制与规划原理[J]. 城市规划,2004,(10):62-67.

[13] 陈益明,刘坤,郑涛,徐竟成. 城市污水回用现状及发展趋势[J]. 净水技术,2003,(5):34-36.

[14] 夏岑岭.城市防洪理论与实践[M].合肥:安徽科学技术出版社,2001.

[15] 林洪孝.城市水务系统与管理[M].北京:中国水利水电出版社,2009.