开放Petri网可达状态求解系统的开发与实现

吴亚光

摘要：Petri网模型是理论计算机科学包括自动机模型和形式语言理论的一个分支，具有自然、直观、简单易懂等特点。开放Petri网是Petri网的一种扩充，在并行模型分析，协议的验证，自动控制等方面有广泛的应用。该文的主要工作在于开发一个可以生成开放Petri网的软件，并能够求解其所有的可达状态，最后通过这样一个软件来研究开放Petri网的可达状态总数随网的规模变化和初始Token数变化而变化的情况。我们得到的结论是在这两种情况下可达状态数都是呈指数增长的。

关键词：开放Petri网 ； Petri网生成 ； 可达状态 ； Petri网规模

中图分类号：TP393 文献标识码：A 文章编号：1009-3044（2016）02-0213-03

Abstract： The model of Petri Net is a branch of theoretical computer science with automaton model and theory of formal language. It is nature， intuitive and easy understanding. Open Petri Net is an expansion of Petri Net and widely used in analysis of parallel model， protocol verification and automatic control. The main work of this subject is to develop a software to build a open Petri Net and calculate all its reachable markings， which meanwhile outputs them. In the end we study the changes of reachable markings when the scale of Nets is increasing by the software. The conclusion we got is that the reachable markings are growing exponentially when the scale of Petri Nets and the initial Tokens are increasing.

Key words： Open Petri Nets； Generation of Petri Nets； Collection of Reachable Markings； Scale of a Petri Net

1 问题的提出

在Petri网研究与应用的发展历史中，它的应用范围已经远远超出了计算机科学的领域，成为研究离散事件动态系统的一种有用工具。如今，Petri网模型在众多方面得以应用，如分布式软件系统，分布式数据库系统，并发并行计算，柔性制造系统，多处理机系统，逻辑推理，办公自动化系统，形式语言，神经元网络和决策模型等。Petri网在如今各个科学领域都已经有了重要的地位，Petri网的分析方法和应用范畴也在被不断扩展，因此实用的Petri分析工具的开发研制也受到各国Petri网研究者的重视。

可达性研究是研究一个Petri网的可能达到的状态和各个状态之间的关系。我们想清楚得到需要研究的网的每个可达状态和它们之间的关系，通过研究开放Petri网的可达状态随着网的规模的变化而变化的情况，来给基于Petri网建模的实际应用系统的研究提供依据，这也就是本文的研究意义。

由于Petri网研究在各个领域的重要意义，我们希望能够开发一个用于计算并输出开放Petri网可达状态的可视化软件，并以此来研究开放Petri网的可达状态数随网规模变化而变化的情况

2 算法实现

2.1 画图界面的算法

在软件运行以后，先选择工具栏上的一个按钮，在空白的空间上进行绘制。绘制会启动一个鼠标左键的点击判定（OnLButtonDown）。如果选择的是添加库所按钮，则先判断改点与已有的库所或者变迁点之间的距离（DistanceBetweenPoints），如果该距离过小，则无法添加，这也是防止两个库所或者变迁元素在图形上过近甚至重合，影响图形的正确性和美观。如果是安全距离，则将库所数（PlaceNum）加1，并将目前的PlaceNum-1作为该库所的标识。同理如果点击的是添加变迁按钮，经过相同的判断来决定添加情况。

如果选择的是添加流关系按钮（界面上显示是箭头），则需要通过以下步骤的验证：

1）通过起始点（FirstPoint）的坐标读取该点的数据，判断它是库所还是变迁。

2）通过终点（SecondPoint）的坐标读取该点的数据，判断它是库所还是变迁。

3）如果两者性质不同，则建立两者间的连线，并将存储网中库所和变迁关系的数组Connec[100][100]中的相应项置为1，表示库所和变迁的连接，否则视为无效操作。

如果选择的是库所删除或者变迁删除按钮，则需要通过以下步骤的验证：

1）通过鼠标所在的坐标确定该点的性质。

2）如果是库所（变迁）的话则删除该元素点，找出标识小于该库所（变迁）的库所（变迁），将其标识减1，并在Connec[100][100]数组中把所有关于该库所（变迁）的数置为0，表现为删除所有关于该库所（变迁）的连接。

如果是流关系删除按钮，则在Connec[100][100]中将该连接的数据置为0，并表现为删除该箭头。

2.2 可达状态计算的算法

按提示输入各个库所的标识（token）数，点击计算结果按钮，会在下面的框中出现所有的可达状态并统计其数量。下面我们先从整体上讨论一下算法的思想。算法包含以下几个函数：

GatherData（）：比较TempToken数组中的标识是否与Token数组中已有的各组标识，若和已有的标识组完全不同，则将TempToken中的标识作为新的一组标识统计到Token数组中，表示又得到一组新的可达状态，否则舍弃。这里我们定义一个变量k=库所数量，利用一个嵌套的循环来逐个比较临时状态数组TempToken和已有的Token数组里面的状态，如果不是每一个都相等那么k将通过自减运算成为0，触发下一个循环，将TempToken里的状态复制到Token数组中存储，并将总的状态数DifferCount加1。如果循环过后k等于0，那么说明TempToken中的状态是和已有的状态之一重复的，那么我们在这里break，继续下一步的动作。

Fire（）：这个函数里面我们先定义了两个容器test和canf，然后同样通过一个循环来依次检测当前token数下的每一个变迁是否可以触发。我们下面用一段伪代码来简单说明一下具体的算法思想。

当一个变迁T的所有前置库所P都至少有一个Token，那么该变迁是可以激发的。激发之后该变迁的每个前置库所的Token减1，每个后置库所的Token加1。可激发的算法运行时先检测Connec数组中与当前变迁有关的部分，如果Connec[P][T]=-1，说明P是该变迁的前置，如果Connec[P][T]=1，则P是该变迁的后置。容器test的作用是存储该变迁每个前置库所是否有Token，如果有Token则在test中存入1，没有就存入0，最后让test容器中的所有数自乘，如果得到的数非0，则表示该变迁的每个前置库所都是有Token的，也就是说该变迁可以触发，如果得到的数是0，则表明该变迁的前置库所中必然至少有一个的Token数为0，也就是该变迁在当前状态下不能触发。这样用循环依次检测以后将可以触发的变迁T存入canf容器中。

完成上面的步骤以后，canf容器中应该都是可以触发的变迁的序号了。依次取出这些序号按顺序触发，触发成功就会将该变迁的前置库所的Token减1，后置库所的Token加1，得到一个新的可达状态，调用GatherData（）函数，将得到的可达状态与已有的Token数组中的状态进行比较来决定是否存储。至此Fire（）函数的功能介绍完毕。

FireSelect（）：从Token数组中依次取出各组标识存入PresentToen进行触发计算，如此往返递归直到Token数组的大小不变为止，即得到了可达状态的总数并且能够输出每个可达状态。

Output（）：输出Token数组中所存储的所有可达状态和它的序号，并通过Num数组的计算输出其直接可达状态的序号，最终输出总的可达状态数。

3 程序功能演示

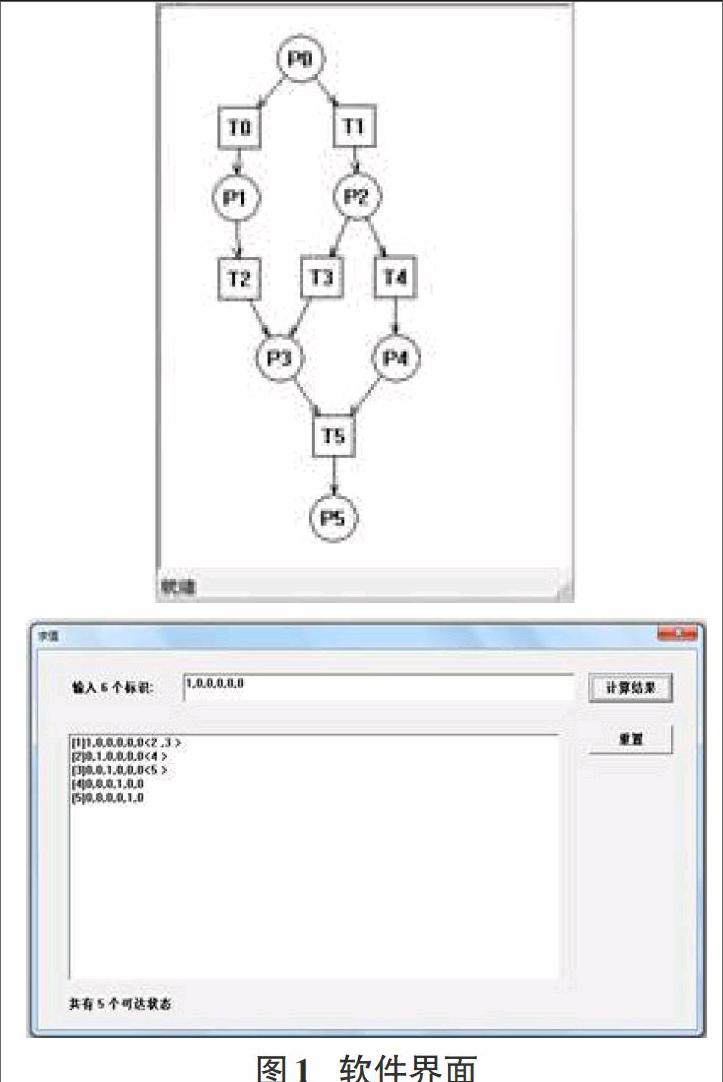
使用Visual C++的MFC对实现上述功能。软件实现界面如图1，左侧为Petri网绘制界面，右侧为可达状态集计算界面。

4 开放Petri网可达状态数变化情况的研究

4.1 可达状态数随初始Token数变化的研究

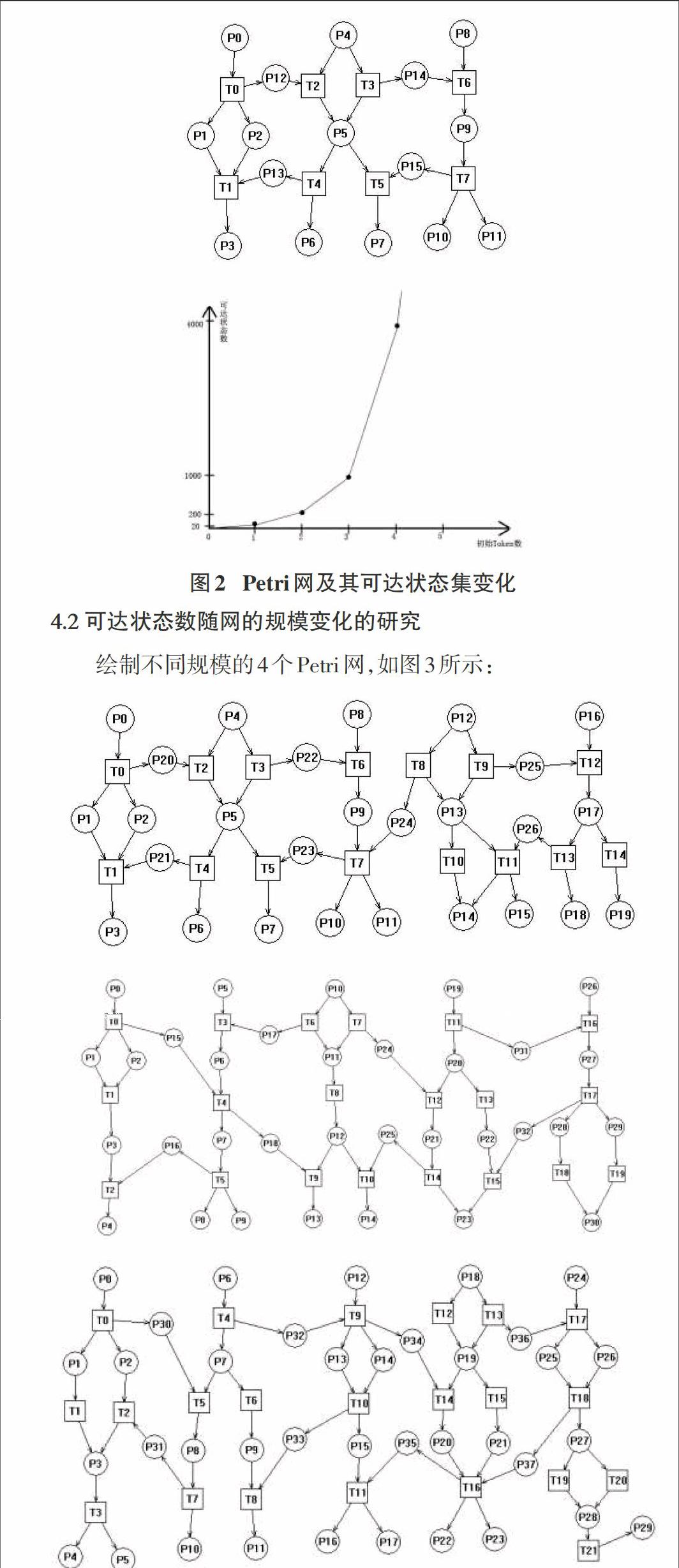
绘制图2左侧的Petri网并按照下列四种情况给Token赋值：

情况1：给库所P0，P4，P8的初始Token置为1，其余库所的Token为全0。运行软件进行计算。

情况2：给库所P0，P4，P8的初始Token置为2，其余库所的Token为全0.运行软件进行计算

情况3：同样的做法，将初始Token置为3，其余全0。

情况4：初始Token为4，其余全0。

最终得到图2右侧的可达状态集变化曲线。

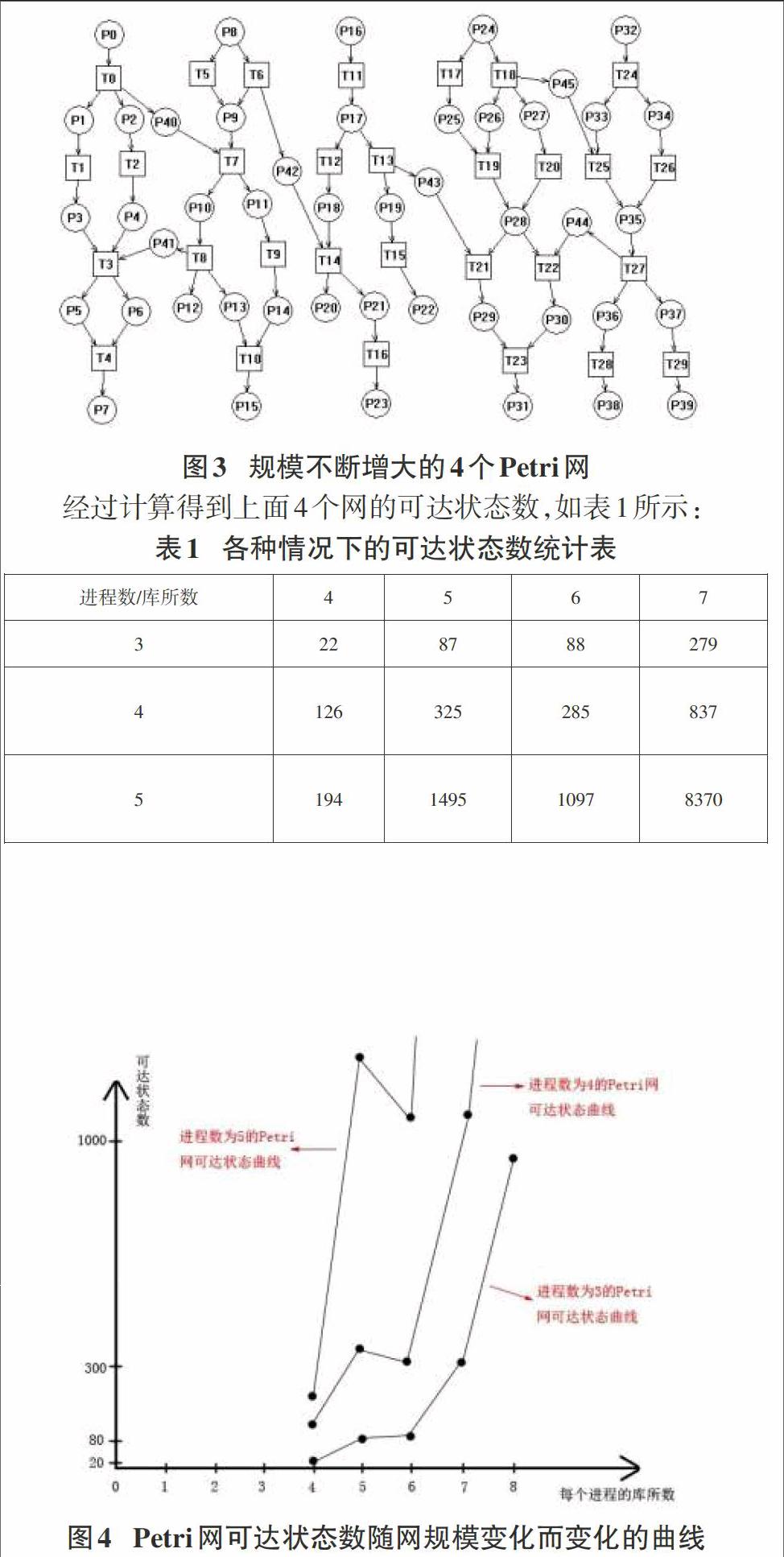
4.2 可达状态数随网的规模变化的研究

绘制不同规模的4个Petri网，如图3所示：

结论：由以上的数据和生成的曲线图可以知道，虽然在每个库所数由5增加到6的时候可达状态不升反减，这可能是由于我们的网都是用户随机生成的，其中的流关系会直接影响到可达状态数的数量，在后来的检查中我们也验证了这一情况。所以总的来说，我们可以很有把握地推断开放Petri网的可达状态数是随Petri网规模的增大而指数增长的。

5 结束语

本文给出了开放Petri网生成及其可达状态集计算的算法，并用C++语言进行实现，编写出了绘制和计算可达状态集的界面。使用该软件分别对开放Petri网随其初始Token数和网的规模变化而变化的情况进行分析，最终得到开放Petri网的可达状态数在上述两种情况下都是呈指数增长的。

参考文献：

[1] （德）Petri C A. Fundamentals of a Theory of Asynchronous Information Flow[J]. Proceedings of IFIP Congress 62，1963，12（4）：86-90.

[2] 吴哲辉. Petri网导论（重点大学计算机教材）[M]. 北京：机械工业出版社， 2006：56-62.

[3] Enric Pastor， Jordi Cortadella， Oriol Roig. Symbolic Analysis of BoundedPetri Nets[J]. IEEE Transaction On Computers，2001，50（5）： 432-448.

[4] 袁崇义.Petri网原理[M]. 北京：电子工业出版社，1998：13-22.

[5] 林闯. 随机Petri网和系统性能评价[M]. 北京：清华大学出版社，2000：89-120.

[6] Murata T. Petri Nets： Properties， Analysis and Applications[J].Proceedings of the IEEE，1989， 77（4）： 541-580.