一种基于分布式CDS的Adhoc网络方法

季梦清

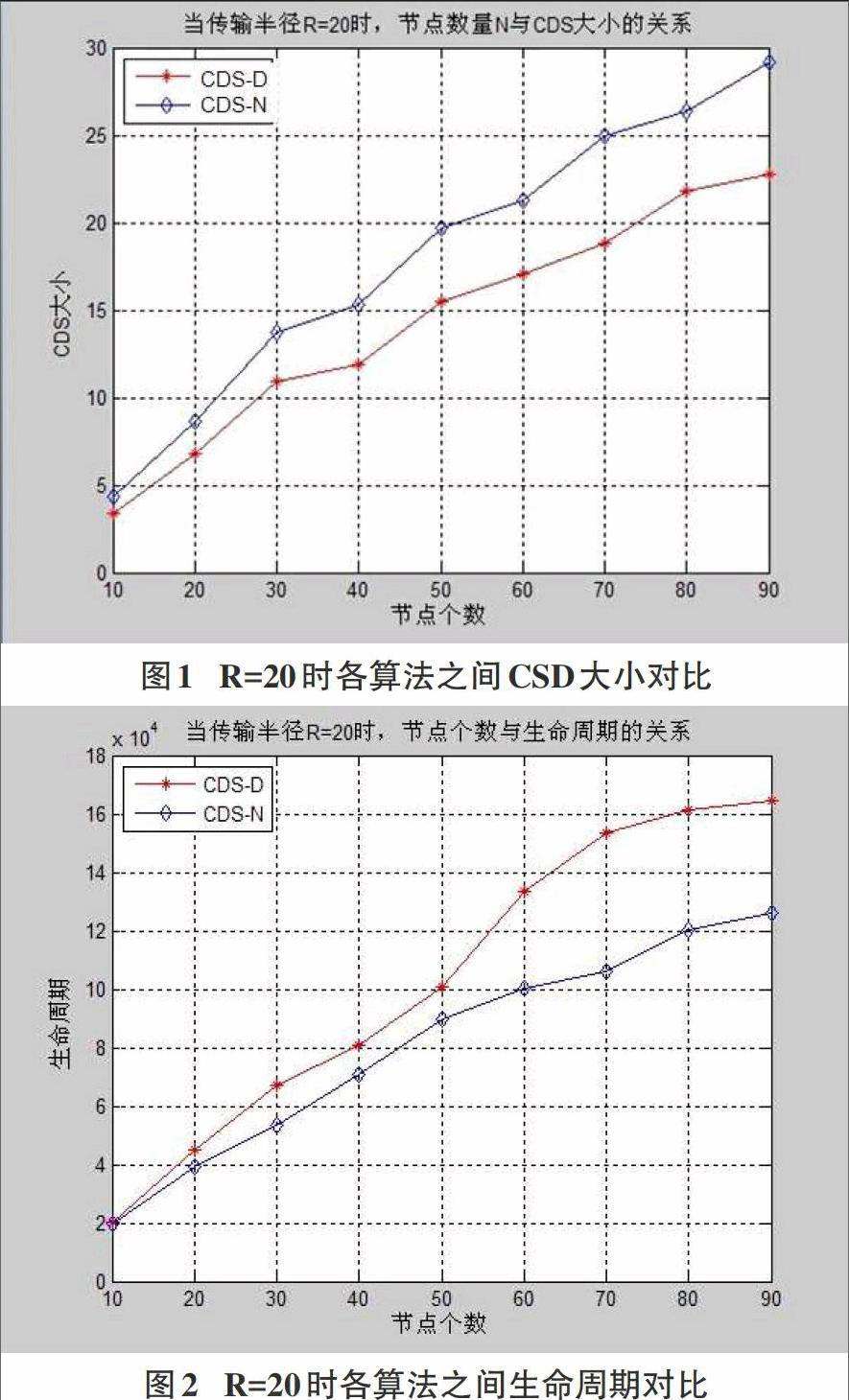
摘要：传统的CSD集中式算法因为考虑较为单一，所产生的CDS不够稳定。针对这个问题，设计实现了对应的CDS分布式算法，并从节点剩余能量，度以及ID三方面进行节点选取。通过对比实验，从形成的CDS大小，网络生命周期等方面，验证了CDS分布式算法的有效性。

关键词： Ad hoc网络；虚拟骨干网；连通支配集；分布式算法

中图分类号：TP393.08 文献标识码：A 文章编号：1009-3044（2016）02-0178-03

Abstract： Existing CSD distributed algorithms for generating CSD consider singlely so that the generated CSD is not stable enough. In order to solve this problem， the distributed algorithm for generating CSD in this paper combines with residual energy， degree and ID to select node in CSD. Experiments show that the proposed method can achieve the desired effect from the aspects of the size of CSD and life cycle of network.

Key words： Ad hoc network； virtual backbone； connected dominating set； distributed algorithm

1 引言

目前，无线局域网（IEEE802.11和HiperLAN）、蜂窝数字式分组数据交换网（CDPD）、家庭无线网（Home RF）、蓝牙 （Bluetooth）[1]等新移动通信技术的相继涌现，并且无线通信网络在全球范围内都已经被广泛地使用。它们的运行通常要基于事先架设的网络基础设施，当灾难发生，网络设备被毁坏时，这些网络完全无法工作。此时我们需要一种能够快速自动组网的临时的移动通信技术，也就是Ad hoc网络技术[2，3]。它是一种无线通信网络，其特点为无中心、多跳、自组织[4]，整个网络没有固定的基础设施，每个节点都能以任意方式动态地保持与其他节点的联系，并且都是移动的。

在Ad hoc网络中的移动节点都同时担当着主机和独立路由的双重功能，但节点在能量供应、网络带宽、计等各方面都有制约，因此我们需要综合各节点的资源选取出骨干节点用于承担网络的通信。关于骨干节点的选取，目前主要的方法有CDS算法[3]，主要分为两类：集中式，分布式。集中式算法需要用到整个网络的拓扑信息，这对于缺乏中心控制的Ad hoc网络来说是难以实现的，因此我们就要引入CDS集中式算法的分布版本。它只需要相邻节点之间的信息即可获得骨干网，不过由于它应用的是相邻节点之间的信息。根据节点的能量，度等选举出Ad hoc网络当中的骨干节点，使得网络的网络能量消耗达到平衡，延长网络的寿命。又由于集中式算法需要全局拓扑信息难以实现，所以有实现CDS分布式算法的必要。

CDS分布式算法[5-7]由于其现实意义成为了当前研究的热点。文献[7]的算法，唯一的ID是区别每个节点的标志。由于算法对于节点的选择因素考虑比较单一，所以产生的CDS相对较大，且有巨大的维护开销将被花费在从根节点出发形成生成树的过程当中。因此，在本文算法中我们综合考虑各方面的关键因素，将节点剩余能量，度等作为选择CSD节点的标准，使得生成的CSD能够尽可能的稳健。

2 分布式CDS算法

本文将连通支配集分布式算法简称为CDS-D算法。本算法是对CDS集中式算法的分布式版本，只利用相邻节点即一跳节点之间的信息进行实现与维护，大致分为节点分层，节点染色以及优化三个阶段。

在算法中的被支配节点的颜色为gray或者white，支配节点的颜色为black或者blue，本算法初始状态每个节点的颜色为white，并根据算法成为black或者gray节点。blue节点只能由gray转化而来，并且不能再改变。每个节点颜色变化后都要与相邻节点广播自己的状态。算法所运用的规则如下所示：

rule 1 当某个节点变为支配节点，则将其周围一跳非支配（white或者gray）邻节点染为gray。

rule 2 根节点将自己染为black。

rule 3 对于节点x，如果自己的父节点或者比自己权重更大的兄弟节点中存在支配节点，则x保持原状态不变。

2.1 节点分层

（1）选择根节点r。

（2）利用分布式BFS算法将所有节点分成不同的等级。

（3）令数组V[k][] = {y ∈v | hopdist（r， y） = k}表示与根节点最短跳数为k的节点的集合。

显然k的最小值为0，可能的最大值为总节点数N-1；

当k = 0时，V[k][]中只放入根节点r，k=k+1，并对所有根节点的邻节点进行广播，即此时节点r为他们的父节点；

当k = 1时，V[k][] = { y∈v| hopdist （r， y） = 1}，即与根节点r相邻的所有节点，根据V[0][]与V[1][]确定出V[1][]层所有节点的父节点与兄弟节点，并对其进行广播，k = k+1；

当k>=2且k<=N-1时，对于任意的节点x∈V[k-1][]，对其进行如下操作：{y∈v| hopdist（x， y） = 1}-{a∈v| hopdist（x， a） = 1&&a∈V[k-1][]}- {b∈v| hopdist（x ，b） = 1&&b∈V[k-2][]}，即从x的所有相邻节点中除去位于V[k-1][]层与V[k-2][]的节点即为与x相邻的V[k][]层中的顶点集合，根据V[k-1][]与V[k-2][]确定出V[k][]层所有节点的父节点与兄弟节点，并对其进行广播，对V[k-1][]层中的每个节点进行上述操作，便可得到V[k][]中的所有节点，k = k+1。