基于SPI和Copula的湟水流域干旱趋势研究

苏夏羿，张 鑫，王 云，王文亚(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

由于气候变化导致的水资源在时间和空间上的重新分配，以及质量和数量上的改变，区域旱涝灾害发生的频率有所增加[1]。近年来全国旱涝灾害频发，西北干旱地区更是首当其冲。湟水河是黄河上游的一级支流，主要由湟水干流和大通河构成，湟水干流全长为374 km，流域面积17 733 km2[2]。湟水流域位于黄土高原与青藏高原的交错地带，属高原大陆性气候，流域内降水地区分布很不均匀，西北部高原地带气温低、蒸发少，植被覆盖率大，降水整体上从西北到东南部递减，并且干、湿季节明显，降水高度集中于5-9月[3]。尽管湟水流域面积仅占青海省土地面积的2.3%，却养育了青海省56%的人口并贡献了48%的GDP[4]。流域中部和东南部地势相对较低，俗称湟水谷地，土壤肥沃、农业资源优越，是青海省东部农业区的主要生产基地，也是青海省政治、经济、文化、交通中心区域。杨发源[5]在对湟水流域研究时得出20世纪90年代后出现了气温升高、降水减少和蒸发量增大的干旱化趋势的结论，可见，对湟水流域干旱趋势的研究很有必要。

在众多的干旱指标当中，标准降水指标(SPI)计算简单，能较好地反映干旱历时和干旱严重程度，广泛应用于干旱监测与评估中[6]。姚瑶[7]和刘蕾[8]已将SPI指数应用于青海东部农业区研究，通过与实际干旱事件的比对，得出SPI能反映该区气象干旱的实际情况的结论。湟水流域中西部和南部均属于青海农业区，故本研究选取SPI作为气象干旱检测指标，结合游程理论对降水序列进行干旱识别，获得干旱历时和相应干旱严重程度序列。基于copula函数在极端水文事件中的广泛应用[9,10]，本文采用Copula函数将干旱历时和干旱严重程度这两个显著相关但服从不同分布的极值事件联合起来，计算干旱历时和干旱严重程度中有一个大于某一定值的“或”联合重现期和两者同时大于等于某一定值的“且”联合重现期，从而全面且系统地对湟水流域干旱趋势分析，为当地的干旱研究及水资源管理提供科学有效的依据。

1 材料与方法

1.1 数据来源

本文选取湟水河流域及周边17个气象站的1960-2006年日降水序列作为研究对象，其中乌鞘岭和皋兰站数据来源于中国气象数据共享网，其余15站数据均为气象站实测资料。湟水河流域以及气象站点所在位置如图1所示。所有站的降水数据均通过了三性审查。

图1 湟水流域以及气象站点位置示意图Fig.1 The schematic diagram of Huangshui River Basin and meteorological stations

1.2 干旱事件识别

不同时间尺度下的SPI值具有不同的物理意义，一般认为6个月尺度的SPI值可以很好地反映气象干旱。为了更好地研究湟水流域干旱的趋势变化，本文采用SPI6对降水序列进行处理，具体计算过程参考《气象干旱等级》[11]。SPI干旱等级划分如表1所示。

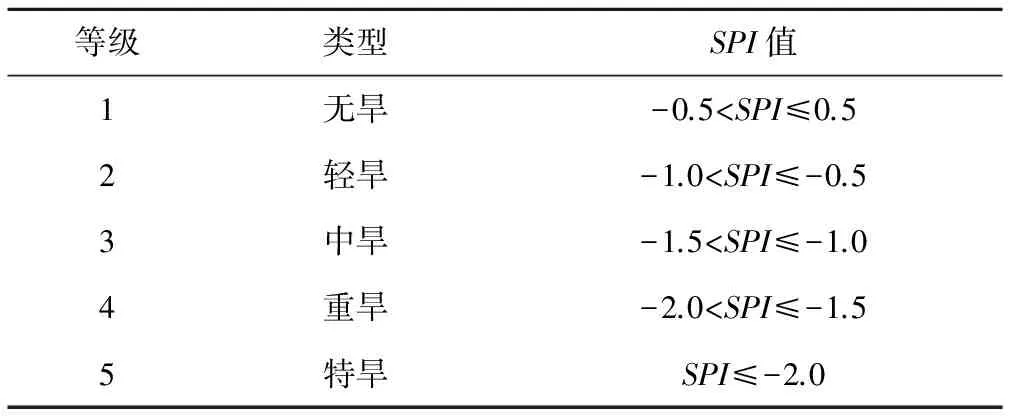
表1 SPI干旱强度等级划分Tab.1 Drought intensity grades of standardized precipitation index

本文选取干旱历时与干旱严重程度来表征一场干旱事件，故需结合划分的干旱等级和游程理论对降水序列进行干旱识别，即定义干旱历时D是SPI6值持续低于-0.5的时间(包括极个别略大于-0.5的月份)，干旱严重程度S为干旱历时内SPI6超出-0.5绝对值的累计值[12]。

(1)

式中：Ii为时段i的SPI值。

计算可获得干旱历时序列和相应的干旱严重程度序列，以及单变量的经验概率分布，此时为离散状态，需通过函数拟合的办法进行处理。本文采用指数分布对干旱历时进行拟合，采用威布尔分布对干旱严重程度进行拟合。各个分布函数的参数均采用最大似然法进行参数估计，并使用Kolmogorov-Smirnov(K-S)法进行非参数检验。

1.3 Mann-Kendall 趋势检验法

假设时间序列(x1,x2,…,xn)无趋势，计算统计量S[13]，计算式如下：

(2)

假设各变量独立同分布，则统计量S近似服从正态分布[13]。其期望和方差分别如下：

(5)

式中：m代表序列中元素相同的组个数；tj代表第j个元素相同组中所包含观测值的个数。

构造M-K统计量Uc：

(5)

假设序列无趋势，当样本数量n比较大时，Uc近似服从标准正态分布，给定显著性水平α，则可根据|Uc|与临界值Uα/2的比较结果判定序列趋势的统计显著性[13]。本文取显著性水平α=0.05。本文主要运用M-K法对17个气象站12个月份的SPI6、干旱历时以及干旱严重程度进行趋势分析，经计算表明这些数据均无明显的自相关性，因此可以采用该方法对其进行趋势分析。

1.4 Copula函数及其参数估计与选择

Sklar定理[14]是Copula函数理论及其应用的基础，阐述了Copula函数构造多元函数联合分布的方法。由Sklar定理可知，F(x1,x2,…,xn)是随机变量(X1,X2,…,Xn)的联合分布函数，其边缘分布函数分别F1(x1),F2(x2),…,Fn(xn)，则存在一个Copula函数C满足：

F(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]

(6)

如果边缘分布函数是连续的，那么C是唯一的。Copula函数可将不同边缘分布的变量构造成联合分布函数，由边际分布和copula函数来确定多变量的联合分布函数。对于干旱历时X与干旱严重程度Y，其边缘分布分别为FX(x)与FY(y)，F(x，y)为其联合分布。

Copula函数有很多种类，本文所使用的是只有一个参数 的二维阿基米德Copulas函数族，包括Gumbel Copulas，Clayton Copulas 和Frank Copulas，对湟水流域的干旱历时和干旱严重程度的联合分布进行拟合。这三种Copula函数的参数θ与干旱历时和严重程度序列的Kendall相关系数系数τ之间有确切的计算表达式(表2)，可据此关系进行参数估算[15]。

表2 Kendall-τ与copula函数的参数θ对应关系表Tab.2 The corresponding relation between the Kendall-τ and the parameter of Copula Function

本文评价上述3种Copula函数对干旱历时和严重程度的拟合优劣的指标值采用均方根误差(RMSE)：

(7)

式中：n为序列样本数；pc为Copula函数在原始点的理论概率分布值；pi为联合经验概率分布值。

优选出拟合效果最好的Copula函数，即为能反映该流域干旱历时和干旱严重程度特征的联合分布函数。为更好反映湟水流域某次干旱事件的干旱历时与干旱严重程度分别大于某一特定值发生的概率，本文计算对应的重现期值，重现期计算公式如下:

(9)

式中:T(X>x, Y>y)为干旱历时与干旱严重程度均超过特定值的重现期，下文称为“且”重现期；T(X>x or Y>y)表示干旱历时或者干旱严重程度超过某一特定值的重现期，称为“或”重现期；P(X>x,Y>y)和P(X>x or Y>y)相应的联合概率密度。重现期大表示出现干旱风险相对较低，重现期小表示出现干旱风险相对较高。

2 结果与分析

2.1 单站逐月SPI趋势分析

当M-K趋势检验法统计量的绝对值大于1.96 时，说明该序列的趋势在95%的置信区间内显著。单点M-K统计量小于零表示该站该月的SPI6序列随时间有减小的趋势，反映在旱涝上是干旱的趋势；大于零表示该站该月的SPI6序列随时间有增大的趋势，反映在旱涝上表示湿润的趋势。湟水河流域各个站点12个月份的SPI6用M-K趋势分析结果如图2所示。图中17个气象站的站点按照经度的大小，从西到东依次排列。

图2 湟水流域17站各月SPI序列趋势分析图Fig.2 Trend graph of SPI in each months at seventeen stations in Huangshui River Basin

由图2可知，湟水流域西北部各站SPI6序列在各月M-K统计量均在-1.96～1.96之间，呈不明显的变化趋势；流域东南部除了华隆和民和站之外其他站点的SPI6序列，均出现了M-K统计量的绝对值大于1.96的情况，呈现显著的变化趋势，并且显著变化的情况集中在乐都、互助、西宁三站，共占总体的55%。只考虑干旱情况时，流域南部的湟源、贵德以及东部的互助、华隆、乐都、民和站几乎每个月份的SPI6值均呈现下降的干旱化趋势。尤其是互助站，所有月份的SPI6序列M-K统计量都小于零，呈现干旱化趋势；并且3月、11月和12月均小于-1.96，呈现显著干旱化趋势。

M-K统计量为大于零集中在6-9月，意味着随时间有变湿润趋势；小于零集中在12月到次年3月，意味着随时间有变干的趋势，这与该流域降水高度集中在5-9月的背景相叠加，势必会造成湟水流域出现干旱的季节更干旱，湿润的季节更湿润的情况，符合气候变化对极端降雨和干旱事件的描述。尤其是乐都站，1月和2月 的M-K统计量均小于-2.3，呈显著干旱化趋势；5-7月SPI的M-K统计量均大于2.1，呈显著湿润化趋势，将增加旱涝灾害的可能，不利于水资源管理。

2.2 干旱历时和严重程度趋势分析

结合SPI值以及游程理论进行干旱识别，获得各站干旱历时与干旱严重程度序列，干旱特征统计情况以及M-K统计量见表3。单站干旱历时的M-K统计量小于零表示该站干旱历时减小的趋势，旱情减弱的的趋势；大于零表示该站干旱历时随时间有增大的趋势，反映出旱情加重趋势。干旱严重程度的M-K统计量表征能力同干旱历时。

表3 湟水流域各站干旱特征统计表Tab.3 Statistical table of drought character at each stations in Huangshui River Basin

由表3可知，除了刚察和乌鞘岭两站，整个湟水流域干旱历时的M-K统计量均在-1.26～1.36之间，干旱严重程度的M-K统计量均在-1.71～1.25之间，均无显著变化趋势。其中流域中部和西部地区干旱历时和严重程度的M-K统计量大部分落在-1～0之间，呈现不显著下降趋势，相比之下，流域东部地区的M-K统计量大于零，意味干旱历时和干旱严重程度有上升的趋势。虽然没有显著干旱等级加重的趋势，但湟水流域这些区域大部分为青海农业区和牧场，依然需要注意轻度等级干旱对农牧业带来的损害，做好防范应对措施。

利用湟水流域各站点干旱历时与干旱严重程度序列的M-K统计量，通过ArcGIS10.0软件的克里格差值法得到整个湟水流域干旱历时与干旱严重程度的增减趋势的空间分布图(图3)。由图可以看出，干旱历时与干旱严重程度的变化趋势在空间分布上存在较好的一致性，历时越长，相对应的干旱严重程度越大。

图3 湟水流域干旱历时与干旱严重程度趋势分析图Fig.3 Trend graph of the drought duration and drought severity in Huangshui River Basin

2.3 典型干旱情景分析

借助SPSS软件单参数K-S检验方法，湟水流域各个站点干旱历时的指数分布和严重程度的威布尔分布均通过了K-S检验。计算两序列的Kendall系数，再依据表1的表达式，对3种Copula函数的参数进行估算，并通过式(5)进行copula函数优选，经计算Frank Copula函数对经验联合分布的拟合效果最好，所以选取Frank Copula作为理论联合分布函数，计算干旱情景下的重现期。

针对不同重现期的计算，结合前人研究，选择两个典型干旱情景：干旱历时大于6个月，基于SPI指数的干旱严重程度大于4表示为联合中度干旱；干旱历时大于8个月，基于SPI指数的干旱严重程度大于6为联合重度干旱。再结合克里格差值法，便可得到整体湟水流域联合中度干旱和中度干旱的重现期空间分布(图4)。

图4 湟水流域典型联合重现期空间分布图Fig.4 Spatial distributions of joint return periods under typical scenarios in Huangshui River Basin

从图4(a)和图4(b)上看，在发生联合中度干旱的情况下，流域东南部的干旱重现期要低于西北部，因此东南部发生中度干旱的风险要高于西北部。湟水流域中度干旱“或”联合重现期平均为13.2年一遇[图4(a)]，“且”联合重现期平均为25.6年一遇[图4(b)]。而位于东南部的民和站，“或”联合重现期和“且”联合重现期分别低至8.9年一遇和17.9年一遇。相比较下，西北部的门源和湟源站“或”和“且”联合重现期均大于14.9年一遇和31.6年一遇，处于干旱低发区。

从图4(c)和图4(d)上看，在发生联合重度干旱的情况下，与中度干旱相似，流域东南部的干旱重现期要低于西北部，东南部发生联合重度干旱的风险要高于西北部。湟水流域重度干旱“或”联合重现期平均为23.7年一遇[图4(c)]，“且”联合重现期平均为59.7年一遇[图4(d)]。最低的民和站“或”和“且”联合重现期分别低至15.5年一遇和34.5年一遇，该站点附近区域重度干旱风险较大，相比之下流域北部和中西部地区重度干旱风险较小。

整体上看，无论对于中度干旱还是重度干旱，湟水流域东南部四种干旱联合重现期均小于西北部，流域东南部发生旱灾的概率均大于西北部。流域北部区域即大通河上游区域，因独特的地理位置，高山环绕，温度低，蒸发量小的原因，无论是何种情境的重现期都相对比较高，发生干旱的可能性较河流下游小。中西部的门源和湟源区域，“或”重现期处在中等水平，而“且”重现期处于大值范围，所以该区域易发生低等级干旱。流域东南部两种情景的“或”与“且”重现期都比较低，所以两种程度干旱均极易发生，应作为流域的干旱敏感区域对待。

3 结 语

(1)本研究采用的标准化降水指数(SPI)对湟水流域17站进行干旱趋势分析，从时间上看，湟水流域出现了干旱的季节更干旱，湿润的季节更湿润的两极化情况。在气候变化的背景下，湟水流域夏旱的情况可能会加重，不利于水资源管理。

(2)从空间上看，流域的东部与南部地区干旱化趋势严重，但通过对干旱历时和干旱严重程度趋势分析，流域各站干旱历时和干旱严重程度的上升趋势不明显，可以得出低等程度的干旱在湟水流域东南部发生的可能性增大的结论。

(3)通过湟水流域17个站点构建Copula函数描述干旱历时和干旱严重程度超过阈值的组合事件重现期，Frank Copula函数对各站的干旱历时和干旱严重程度拟合效果最好，可以用于该区域的干旱分析。从空间分布上看，不管是联合中度干旱还是重度干旱，湟水流域东南部的干旱风险要高于西北部。而流域东南部为需水量大、人口密集的农牧业区，干旱造成的损失更为严重，因此相关部门应加大该区域的干旱预警及监测力度，提前做好应对措施。

SPI指数只是基于降水的气象干旱指标，没有考虑温度、蒸发、地形等因素对干旱的影响，与实际情况存在一定的偏差；并且本文在Copula函数确定干旱评估指标上的研究还不够，有待进一步深入研究。

□

[1] 赵晓慎, 周 海, 王文川. 气候变化对区域水循环系统影响的研究进展[J]. 华北水利水电学院学报, 2012,(2):46-49.

[2] 邱玉利, 周建中, 马 林. 湟水流域地表水资源特征[J]. 水资源与水工程学报, 2007,(6):98-102.

[3] 郭 武. 青海省湟水流域河川径流特征分析[J]. 干旱区研究, 1996,(2):25-30.

[4] 赵串串, 杨晓阳, 张凤臣, 等. 基于生态足迹分析的青海湟水河流域可持续发展能力[J]. 干旱区研究, 2009,(3):326-332.

[5] 杨发源, 戴 升. 湟水河流域水资源变化特征及其对气候的响应[J]. 青海气象, 2010,(3):12-18.

[6] 韩海涛, 胡文超, 陈学君, 等. 三种气象干旱指标的应用比较研究[J]. 干旱地区农业研究, 2009,(1):237-241.

[7] 姚 瑶, 张 鑫, 马 全, 等. 基于SPI青海省东部农业区季节干旱变化分析[J]. 灌溉排水学报, 2013,(6):96-100.

[8] 刘 蕾, 张 鑫, 徐 静.SPI指数和Z指数在青海省东部农业区应用分析[J]. 中国农村水利水电, 2015,(4):97-100.

[9] 陆桂华, 闫桂霞, 吴志勇, 等. 基于copula函数的区域干旱分析方法[J]. 水科学进展, 2010,(2):188-193.

[10] 陈永勤, 孙 鹏, 张 强, 等. 基于Copula的鄱阳湖流域水文干旱频率分析[J]. 自然灾害学报, 2013,(1):75-84.

[11] GB/T 20481-2006，气象干旱等级[S].

[12] 肖名忠, 张 强, 陈晓宏. 基于多变量概率分析的珠江流域干旱特征研究[J]. 地理学报, 2012,(1):83-92.

[13] Kendall M G. Rank correlation methods[M]. London: Griffin, 1975.

[14] Sklar A. Fonctions de repartition an dimensions et leurs marges[J]. Publ Inst Statist Univ Paris, 1959:229-231.

[15] 孙 鹏, 张 强, 陈晓宏. 基于Copula函数的鄱阳湖流域极值流量遭遇频率及灾害风险[J]. 湖泊科学, 2011,(2):183-190.