岩溶塌陷水动力-力学耦合过程数值模拟——以武汉市青菱乡为例

陈冬琴，唐仲华

(1.中国地质大学(武汉)环境学院，武汉 430074；2.湖北城市建设职业技术学院，武汉 430000)

1 研究区岩溶塌陷区地质条件

烽火村乔木湾岩溶塌陷位于武汉市洪山区青菱乡烽火村二、三组，上、下倒口湖之间，东距京广铁路750 m，西距107国道120 m，距长江直线距离1.8 km。1997-2005年先后共发生大小陷坑23处，且近几年有新的塌陷坑形成，陷坑平面形态呈椭圆形，烽火村塌陷坑直径一般<10 m，深跨比≥0.3，认为是相互连通的扰动带和多个土洞发育而引起的塌陷。

垂向上分成三个发育段。

(1)上发育层。溶洞埋深20～40 m，标高段一般为(0～20 m)，钻孔遇洞率15.71%，此埋深段为研究区溶洞垂向发育程度最强。几乎存在于岩溶强发育区及较强发育地区，分布较广泛，面状多发育为溶孔、溶槽的形式，此层溶洞发育规模一般都比较大，最大溶洞高度为7.8 m。

上层发育带分为四段：20～25，25～30，30～35，35～40 m；各埋深段的岩溶发育情况如图1所示。从图中可以看出20～25 m埋深段是一个弱发育段，25～30 m为岩溶最发育段。

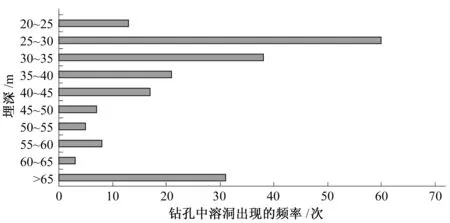
图1 岩溶发育程度与深度关系Fig.1 Degree of karst development vs. the depth

(2)中发育层。埋深在 40～65 m，标高段一般为-20～45 m， 该段岩层溶洞较发育，所有的石灰岩区普遍存在，遍布青菱乡、毛坦港、阮家巷、烽火村等地区，溶洞规模不大，洞高一般在3 m以下，全部分布在塌陷区，表明地表塌陷较深层次的溶洞也起着至关重要的作用。

但50～55 m埋深段、60～65 m埋深段钻孔遇洞率在3%以内，岩溶及溶洞发育相对较少，为岩溶弱发育段。

(3)下发育层。埋深约65 m以下(标高段一般为-45以下)，该段溶洞发育很不均匀，断层带溶洞发育规模较大，最高溶洞达7.08 m，这与地层的构造有密切的关系，此标高段钻孔遇洞率为15.6%，分布在阮家巷及毛坦港附近，全部为重点塌陷区，区内深部岩溶应该较发育。

2 数学模型

2.1 地下水流动数学模型

根据Darcy定律和水均衡原理，忽略密度变化对地下水影响的三维流动数学模型为：

(1)

式中：h(x,y,z,t)为水位，L；Kxx、Kyy和Kzz分别为沿x、y、z主方向的渗透系数，L/T;w为单位体积单位时间内注入或抽出的水量，1/T；μs为单位储水系数，1/L；t为时间，T；h0(x,y,z)为流场初始水位，L；B1为一类边界条件；B2为二类边界条件；q(x,y,z,t)为二类边界上单位面积已知流量，L/T。

2.2 力学模型的简化

假定地层在土压力变化过程中引起的垂向总应力不变，土体侧向变形忽略，只发生垂向变形。土体的有效应力变化及垂向应变为：

有效应力变化为：

(2)

Δσ′z=-αpΔP

(3)

平均有效应力变化为:

(4)

垂向应变为：

(5)

式中：ΔP为压力增量；Δσ′x、Δσ′y和Δσ′z分别为x，y和z三个方向的有效应力变化；Δσ′M为平均有效应力，σ′M=(σ′x+σ′y+σ′z)/3；v为泊松比；K为体积模量；αp为Biot系数；εz为垂向应变。由此模型可以看出，孔隙水压力的增加引起水平有效应力减小；由于地表的自由变形，垂向有效应力只受孔隙水压力变化的影响；垂向应力应变满足线弹性的Hooke定律。

2.3 耦合方法

在初始流场时有相对应初始应力值， 地下水位上升或下降都会引起土体有效应力的变化，利用GMS软件模拟出不同时段地下水的流场值，计算出不同时段的应力，不同时段之间应力差值是压力的增量为ΔP，不同时段之间有效应力差值为Δσ′x、Δσ′y和Δσ′z，再计算出不同时段土体的应力应变。饱和土体的有效应力表达式为：

(6)

2.4 土体破坏判别准则

土体是否产生应力破坏，采用库伦-莫尔准则：

τ=c+σ′ntanφ

(7)

首先需要根据应力状态得到应力莫尔圆，然后确定主应力(有效应力)方向，再得到最有可能发生剪切破坏的方向，最后采用破坏准则判定岩土体是否破坏。

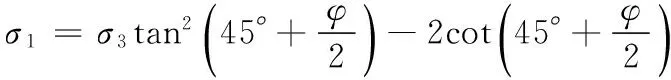
(8)

式中：σ1、σ3最大、最小主应力，上式表明岩土体处于极限平衡状态，还有另外两种情况存在。可以得到如下判别关系式：

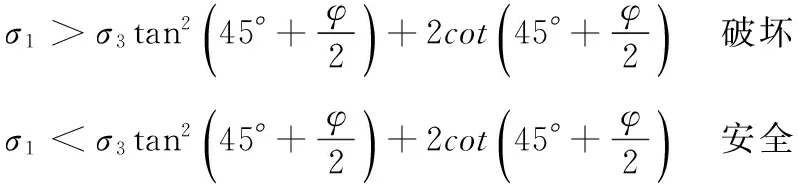
(9)

每一个单元体相应的最大应力及最小主应力为：

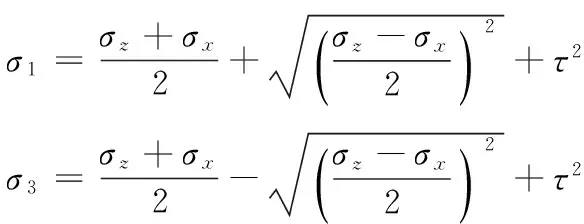
(10)

3 数值模型

3.1 模型边界条件及网格剖分

(1)侧向边界。研究区西临长江，可设此边界为河流边界，根据资料分析，长江历年的平均水位16.70 m，因长江切割了砂层及基岩，且与承压含水层及岩溶水有水力联系，在汛期侧渗补给前缘孔隙水，通过越流形式补给岩溶水，所以砂层以下定为隔水边界，砂层以上至长江底部高程以下定为定流量边界，分段量化补给量。模拟区的东、南、北面边界定为定水头边界，根据观测孔的资料分析得到。

(2)底边界。选在灰岩埋深165 m处，此边界基本没有产生水力交换，可以作为隔水层边界处理。

(3)上边界。潜水层的自由水面作为系统的上边界，作为潜水面边界，系统与外界发生垂向水流交换。如：接受河流渗漏补给、农田灌溉补给、降雨入渗补给、潜水面的蒸发排泄等。各含水层的顶、底板高程根据钻孔资料确定。

通过对该研究区的地质结构模型、地下水水流特征及补、径、排关系分析，将盖层地下水流模型概化为非均质各向同性、三维非稳定流模型。基岩层定义为非均质各向异性、三维非稳定流模型。

把研究区共剖分网格单元6 315个(图2)。垂向上由各含水层底板埋深及厚度决定，总模拟深度180 m。

图2 网格系统Fig.2 Grid system

3.2 模型参数分区及参数值

(1)渗透系数、弹性储水系数、给水度。渗透系数、弹性储水系数、给水度是正确建立水流模型的关键，在空间上具有很强的变异性，本次建立水流模型采用等效厚度法，结合钻孔、地质剖面图、观测孔资料、研究区前人的研究成果确定初始参数值，在模型识别阶段进一步调整，图3为各含水层参数分区图。灰岩及其他基岩的参数根据灰岩的埋藏及覆盖情况进行分区。

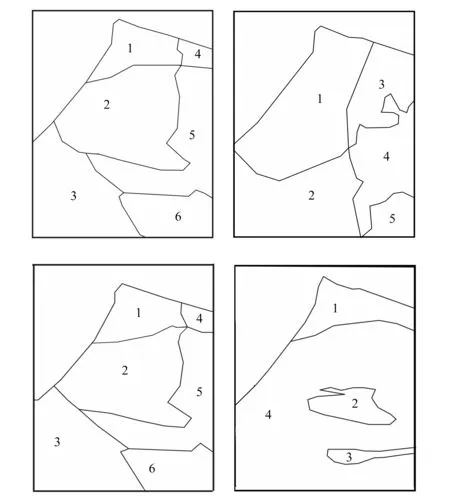
图3 潜水、弱透水层、承压含水层，其他基岩及灰岩参数分区Fig.3 Phreatic aquifer, aquitard, confined aquifer, other bedrock and limestone parameters partition

(2)力学参数初次选取。力学参数有压缩体积模量、回弹体积模量、天然重度、饱和重度、泊松比、黏聚力、摩擦角等。

3.3 模型识别

模型识别的目的是为了提高模型的精度，模型识别的过程是反复调整模型参数(包括边界条件)使计算结果尽可能与实际监测资料一致。模型识别资料选用2009年1月全区的统测水位作为模型识别的初始流场，2012年1月和7月的数据作为拟合检验。

(1)流场拟合。根据2009年1月为初始流场，计算出位于土洞上层即第三层的初始应变值及破坏分布如图4、5所示。

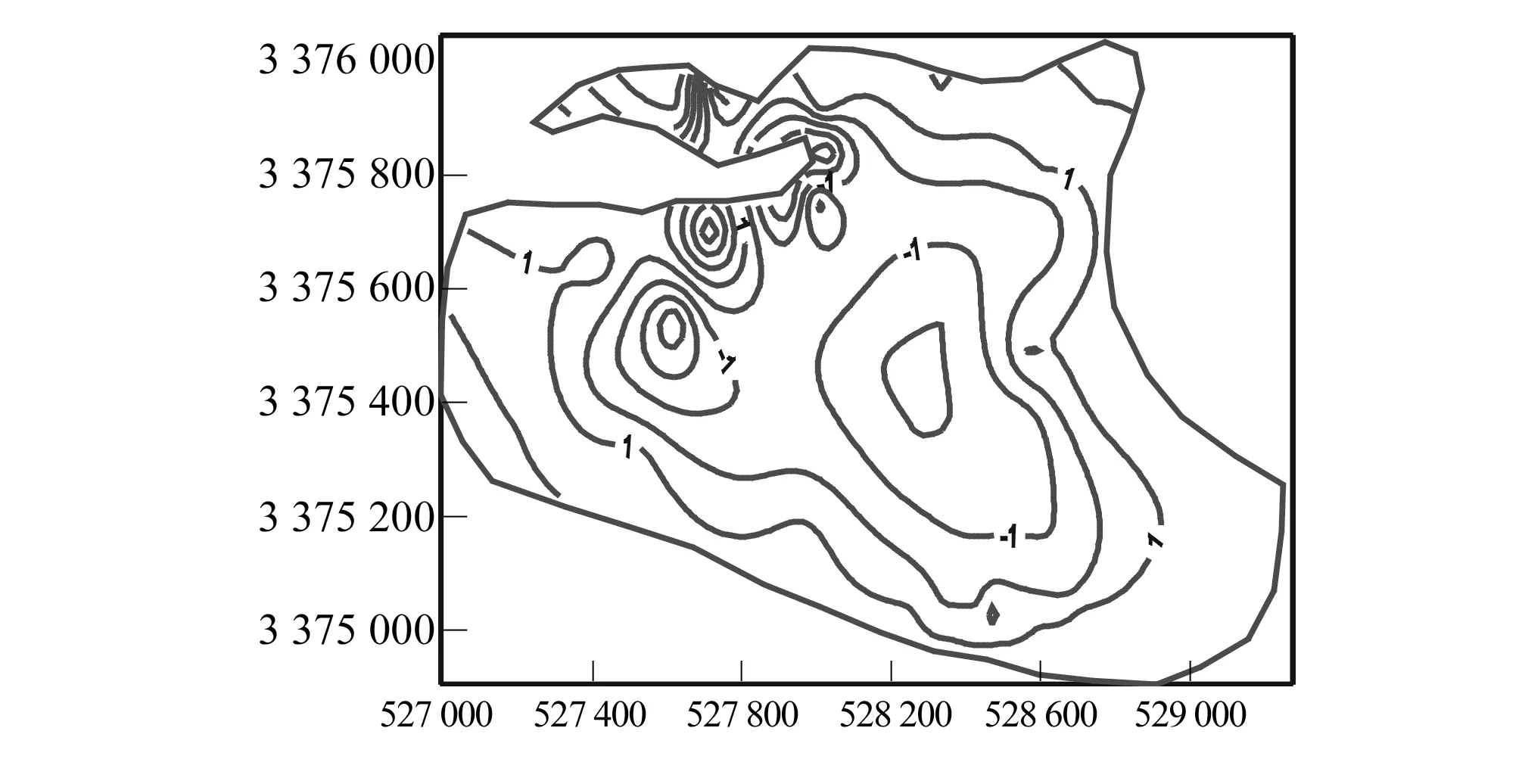
图4 2009年1月第三层垂向应变Fig.4 Vertical strain in lay 3 in January 2009

图5 2009年1月第三层破坏区Fig.5 Destroyed zone in lay 3 in January 2009

1月是武汉地区的枯水期、7月是丰水期，长江水位的上涨、降雨集中在7月，2012年1月流场实测值与计算值比较(图6)、7月土体应变及破坏区的分布情况如图7、8所示。

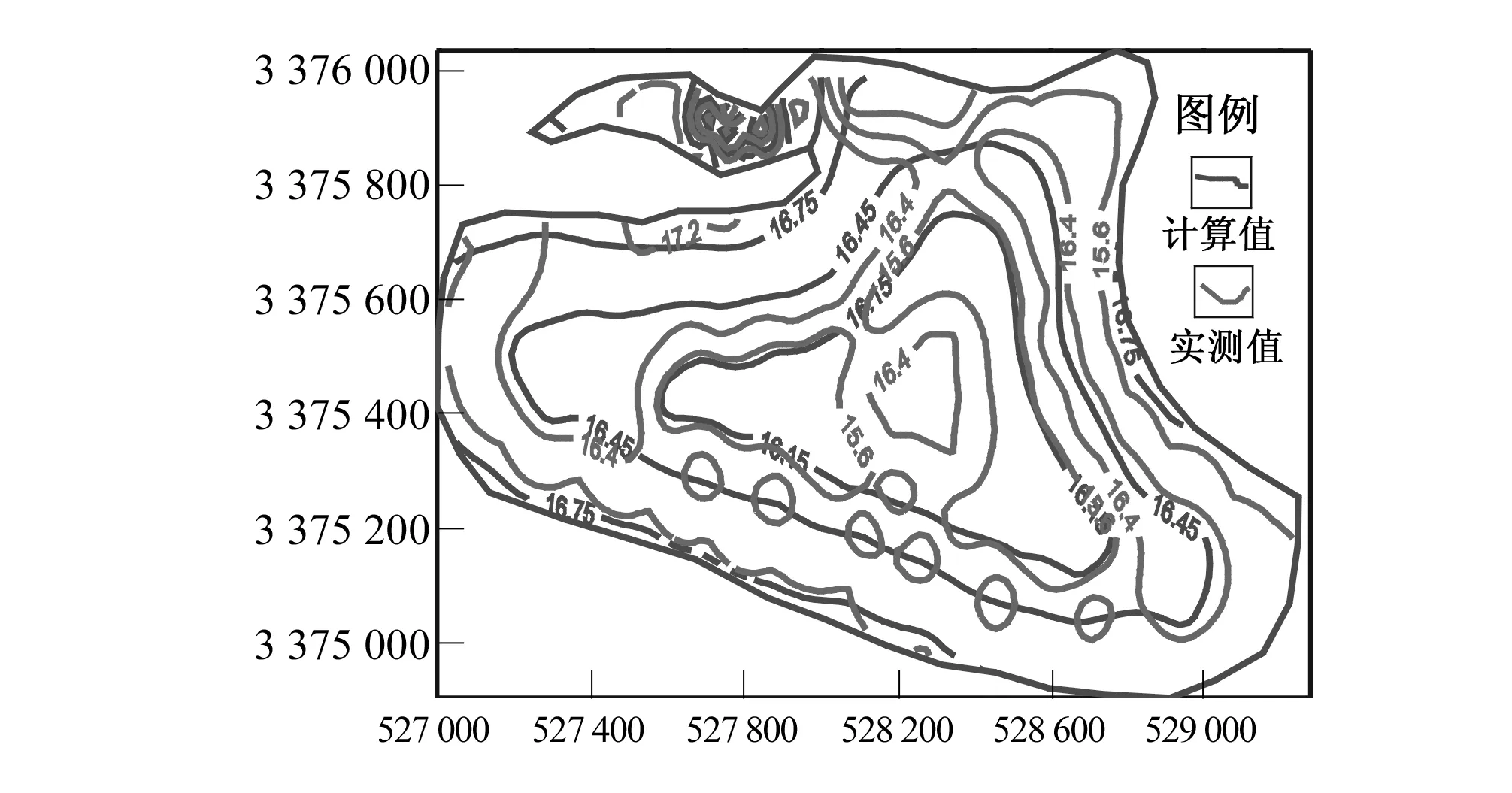
图6 2012年1月第三层地下水流场实测值与计算值比较Fig.6 Comparison of measured and calculated valuesfor groundwater flow field contours in lay 3 in January 2012

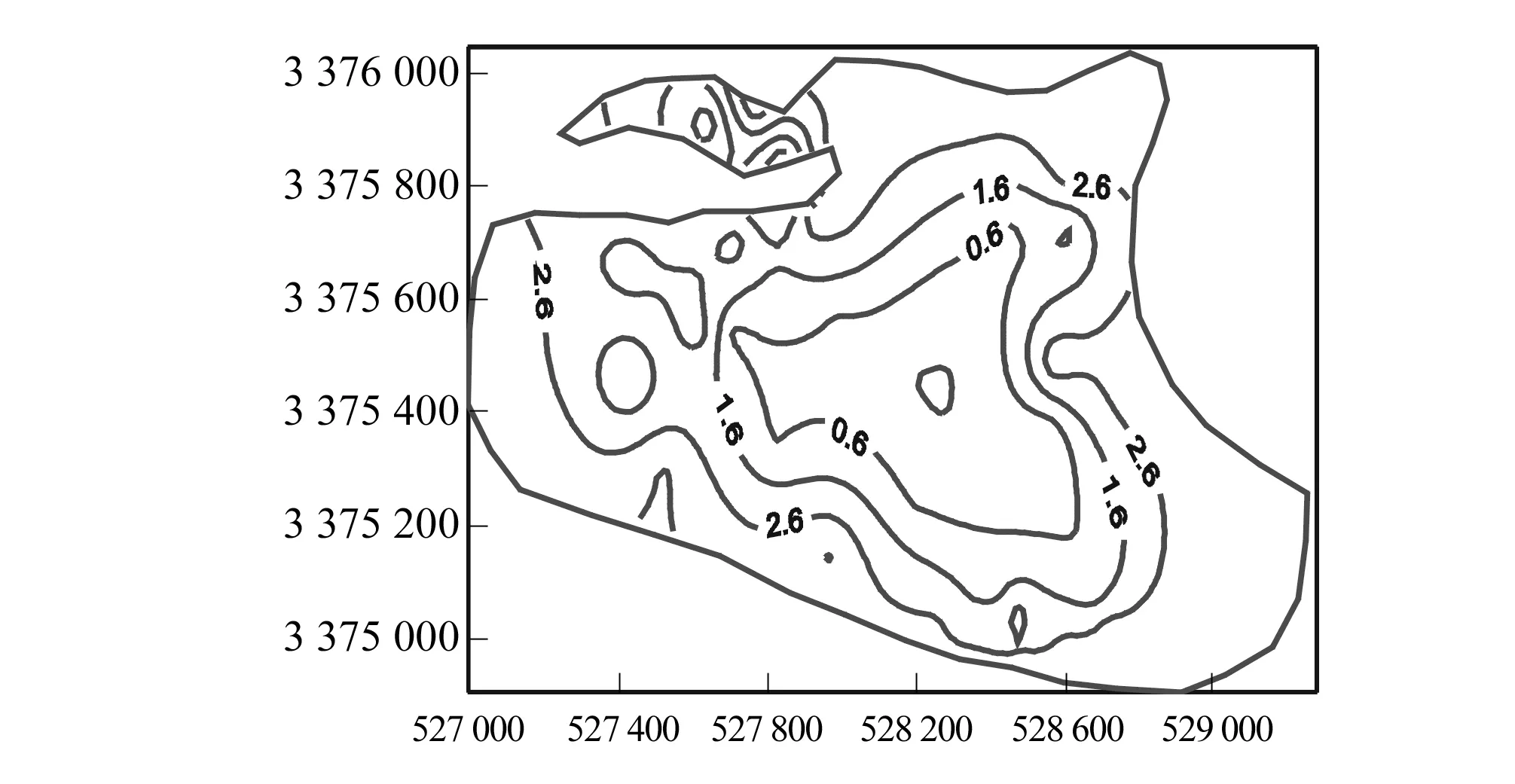
图7 2012年7月第三层垂向应变Fig.7 Vertical strain in lay 3 in July 2012

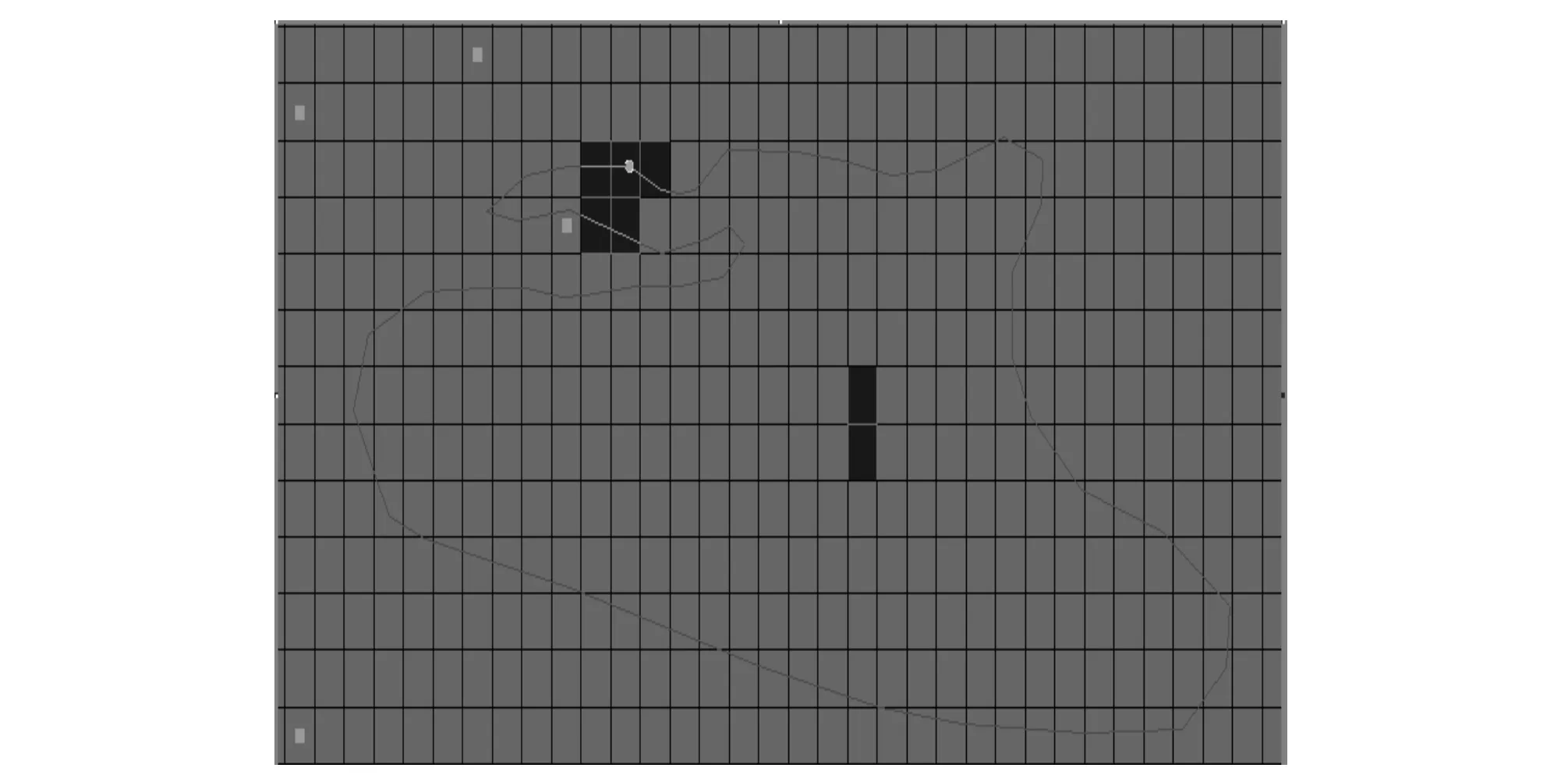
图8 2012年7月第三层破坏区Fig.8 Destroyed zone in lay 3 in July 2012

(2)应力及变形拟合。2012年监测点土压力及土体变形拟合效果如图9、10所示。

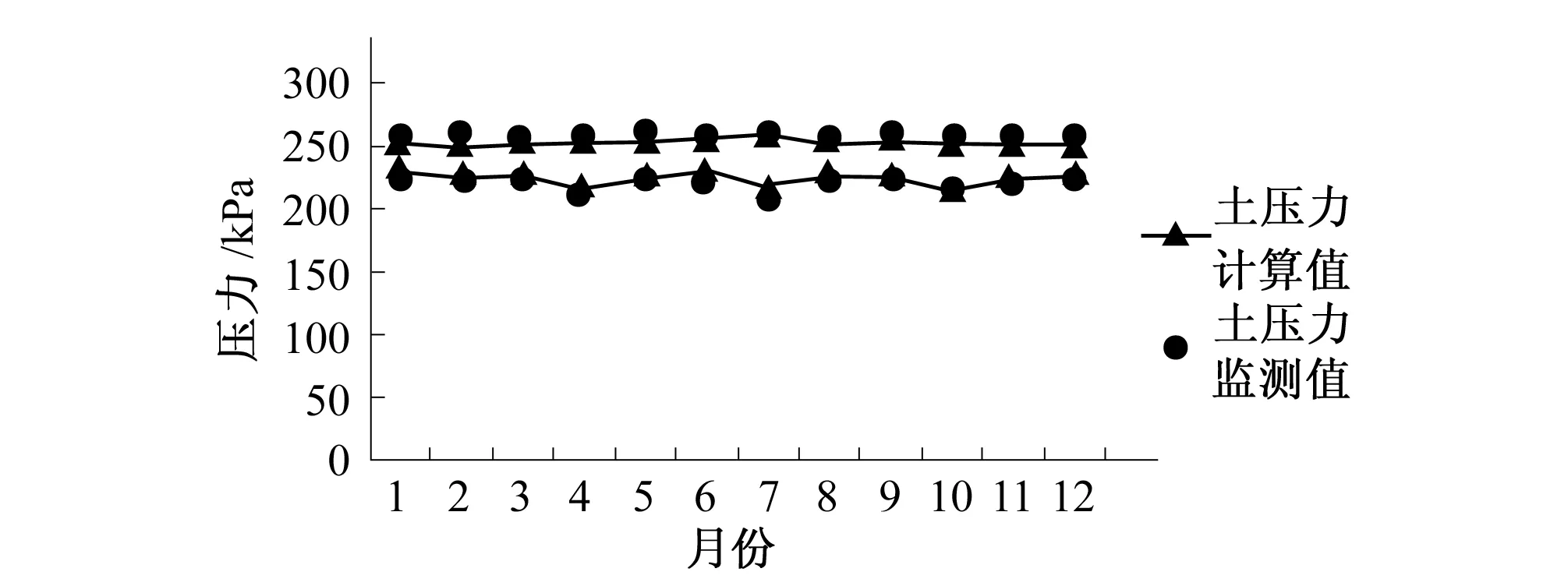
图9 监测点土压力拟合Fig.9 Earth pressure fitting of monitoring points

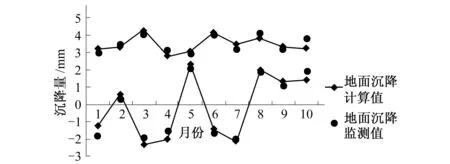
图10 监测点土体变形拟合Fig.10 Soil deformation fitting of monitoring points

(3)模拟结果分析。土体压力自2009年开始模拟计算，模拟数据表明， 2009年1月第三层砂层处于破坏状态，这与2009年发生在烽火村的岩溶塌陷时间一致，2012年7月模拟的土体破坏区与地下水流场变化有着密切的关系，与实际的塌陷点位置相符。充分说明利用流场值模拟土体的变形及岩溶塌陷是可行的。

土体受力状况的变化值受地下水的影响较大，每年的7-8月份相对于全年的土压力值及有效应力值偏低，是由于地下水位明显升高，产生浮托力作用的结果。在模拟的年度内土压力值的震荡性较大，随着地下水位的变化而压实回弹，经过几次回合后，土体出现塑性变形，之后发展到破坏引起岩溶塌陷。

土体垂向变形与地下水的升幅有直接的联系，土体的沉降与回弹与每一层地下的流场走向相符，在没有考虑施加荷载时，土体沉降的变形值一般小于4 mm。

土体破坏规律：地下水的活动和运移，将对土层产生潜蚀作用，从而形成土洞。此外，土洞形成后，其洞壁周围将产生应力集中现象，当地下水位发生变化时(上升或下降时)，将进一步改变洞壁周围土体的应力状态，并致使洞体周边产生破坏最终导致塌陷。

(4)识别后的参数，通过模型识别，得到的模型参数如表1-5所示。

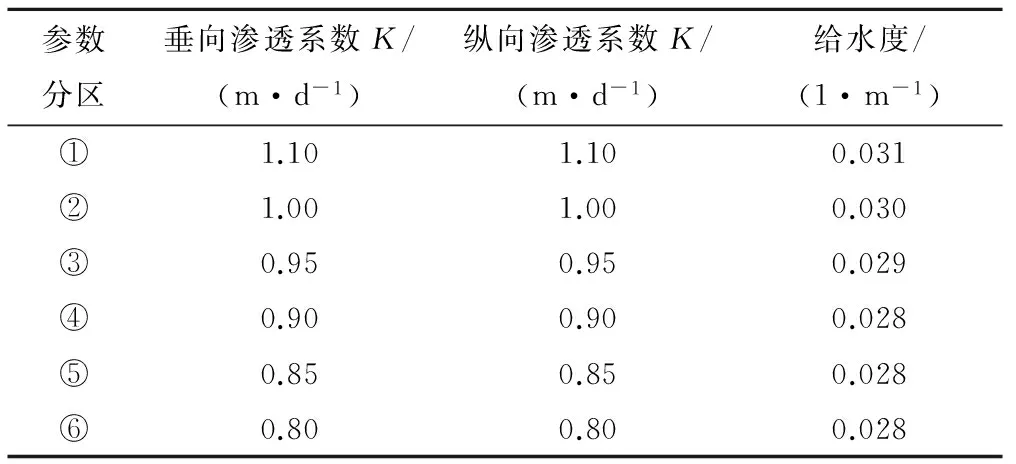
表1 潜水层参数分区表Tab.1 Phreatic aquifer parameters partition table

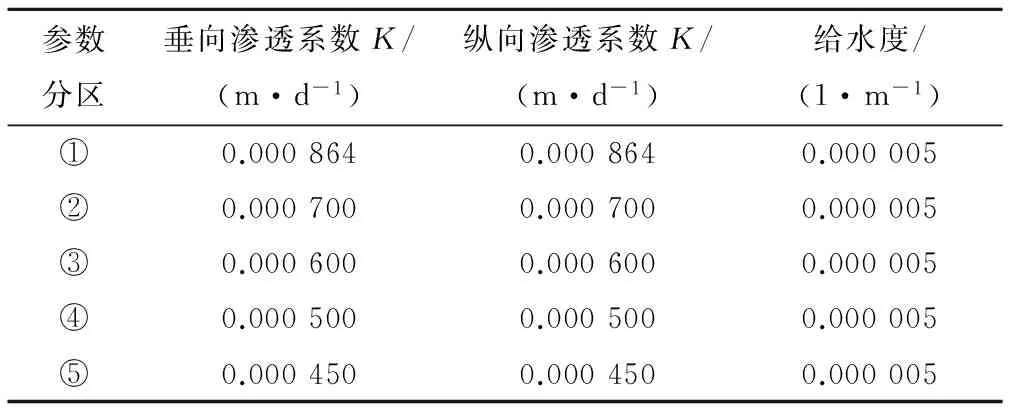
表2 弱透水层参数分区表Tab.2 Aquitard parameters partition table

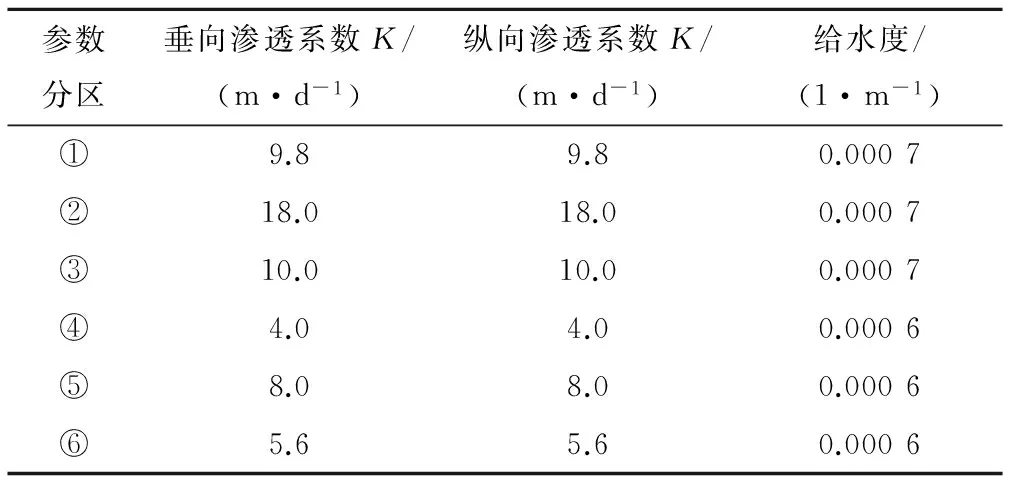
表3 承压含水层参数分区表Tab.3 Confined aquifer parameters Partition table

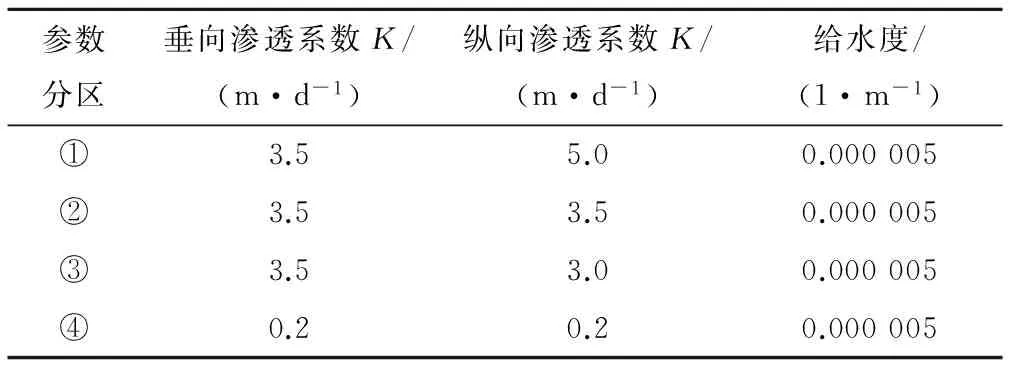
表4 其他基岩及灰岩参数分区表Tab. 4 Other bedrock and limestone parameters Partition table

表5 压缩回弹模型相关参数表Tab.5 The parameters of the compression and springback model

4 岩溶塌陷影响因素模拟评价

4.1 长江水位动态对岩溶塌陷的影响预测

实际调查监测表明，研究区内地下水水位动态受长江水位波动影响明显，地下水位动态与长江水位具有显著的相关性。因此，以长江水位变幅较大的2010年水位动态数据，在其他各项参数及源汇项不变的情况下，模拟预测了长江水位动态对岩溶塌陷的影响。

经过两次交替长江水位上升、下降，土体也经历了回弹、压缩作用，预测的第三层(砂层)应变及土体破坏情况如图11、12所示。结果表明，研究区地下水与长江水位具有很好的连通性，当长江水位在最高水位(年)与最底水位(低)交替出现时，地面塌陷点向长江方向偏移，这与地下水的排泄方向一致，岩溶塌陷很明显是由地下水渗流作用引起。

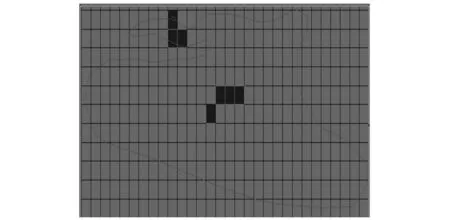
图12 长江水位交替时第三层破坏区Fig.12 Destroyed zone in lay 3 when water level changes in the Yangtze River water

4.2 工程建设排水施工对岩溶塌陷的影响预测

研究区近几年拆迁还建、市政建设等工程大量增加，很多工程涉及到深基坑开挖，为保证施工安全，需要降低地下水。根据施工规范规定，地下水位必须降至基础以下1～1.5 m，一般情况下基础的开挖深度10 m左右，研究区地下水位需降至高程11 m位置。为此，利用数值模型模拟了当某基坑开挖排水时得到的垂向应变及土体破坏情况如图13、14所示。模拟结果显示，土体的垂向应变发生明显变化，从降落漏斗最深处开始破坏。

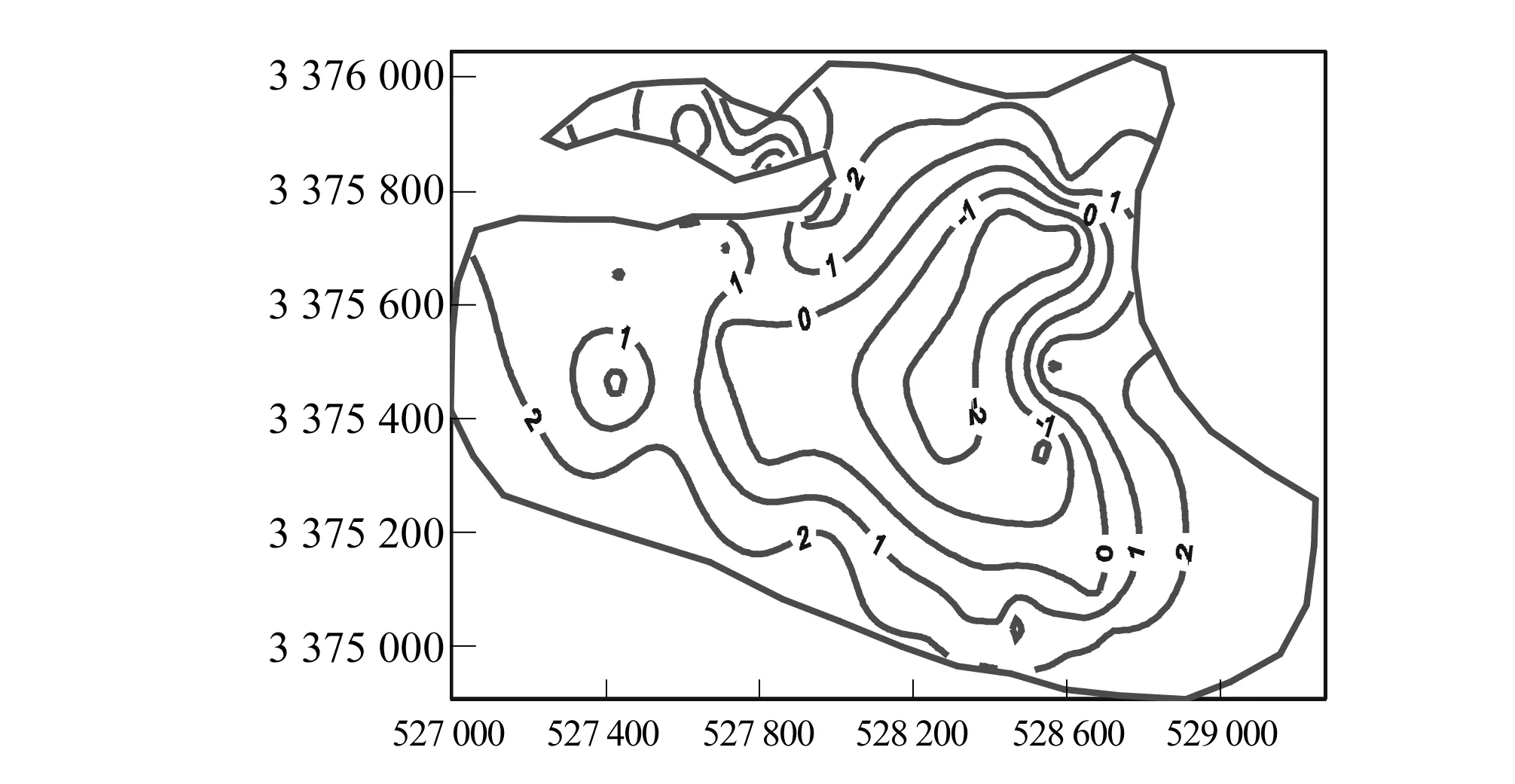
图13 基坑排水第三层垂向应变Fig.13 Vertical strain in lay 3 when drainage of foundation pit

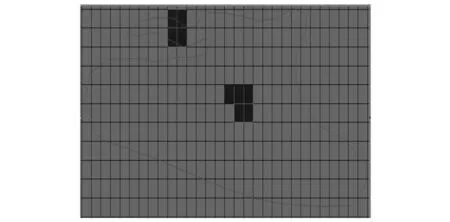
图14 基坑排水第三层破坏区 Fig.14 Destroyed zone in lay 3 when drainage of foundation pit

4.3 大气降水对岩溶塌陷的影响预测

降雨是研究区地面塌陷发生的重要影响因素之一，实际调查表明，研究区内多起地面塌陷的触发因素都是降雨。降雨对地面塌陷的直接作用主要体现在两个方面：使上部土体饱水自重增加，物理力学性质降低；降雨入渗的渗流作用破坏土洞的稳定性。

根据武汉地区的降雨特征，在7月份流场的基础上，通过改变降雨入渗补给量，模拟3种降雨模式(表6)，计算土压力的变化值分析降雨对土体变形及岩溶塌陷的影响。

在补给条件不变的情况下，以上几种降雨模式的土体变形及破坏情况如图15-20。

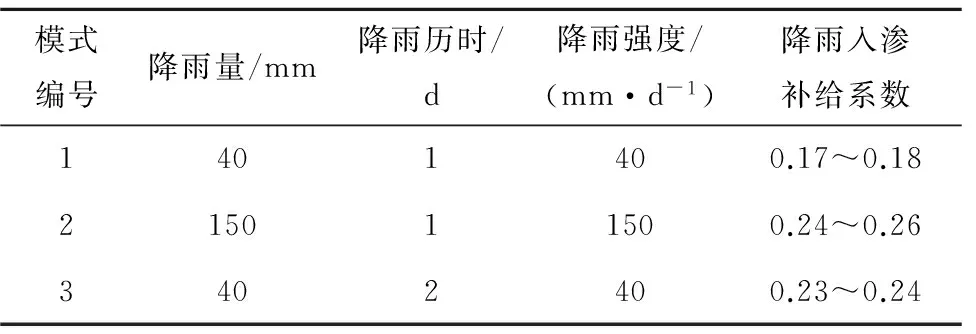
表6 降雨预测模式有以下3种情况Tab.6 Rainfall prediction model has the following three cases

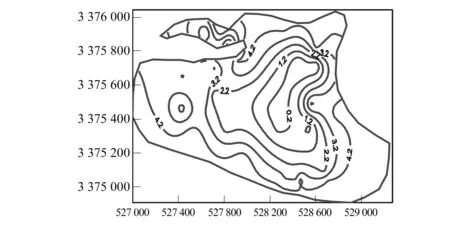
图15 模式1第三层垂向应变Fig.15 Strain contour in Layer 3 for case 1

图16 模式1第三土层破坏区Fig.16 Destroy zone in Layer 3 for case 1

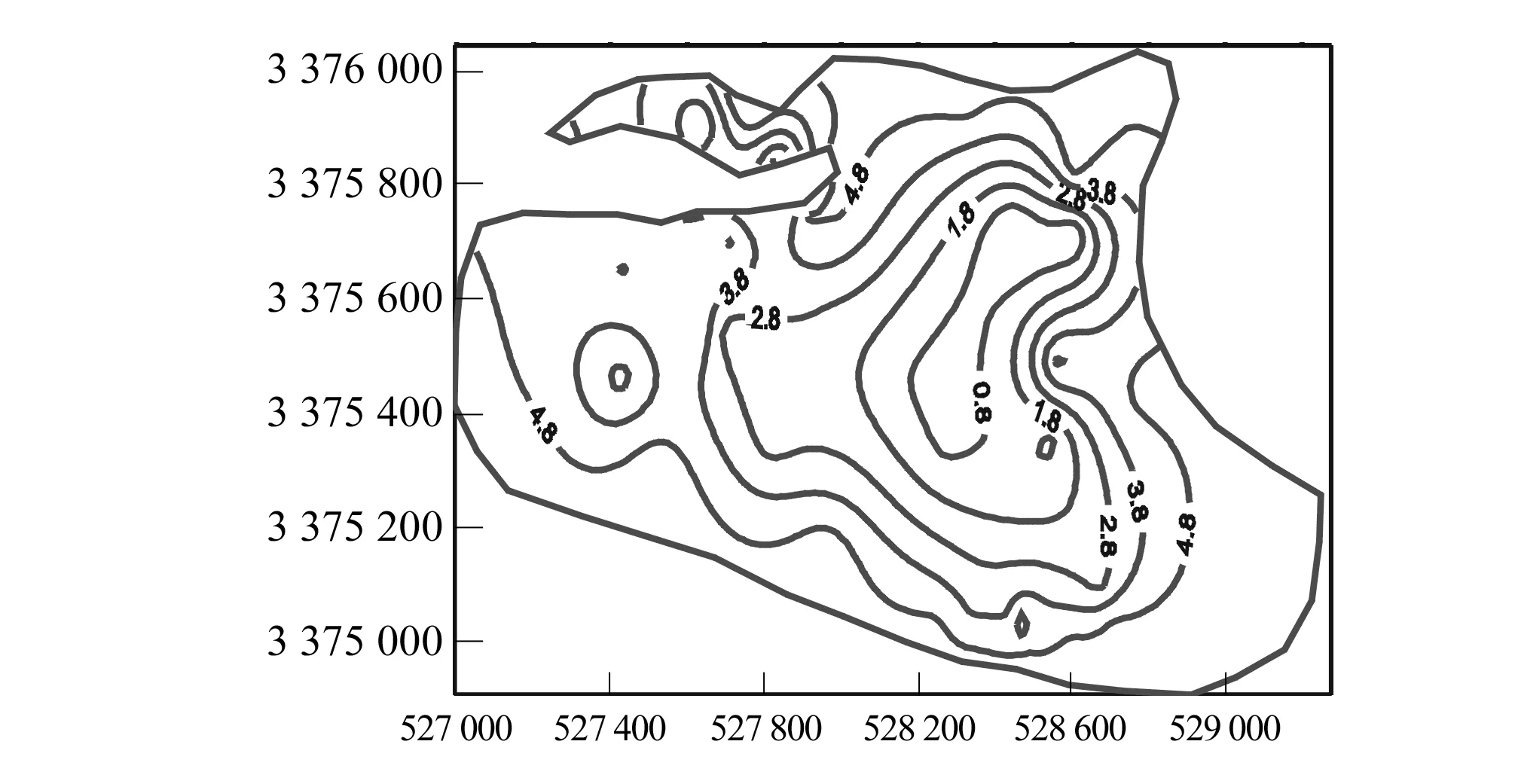
图17 模式2第三层垂向应变Fig.17 Strain contour in Layer 3 for case 2

图18 模式2第三土层破坏区Fig.18 Destroy zone in Layer 3 for case 2

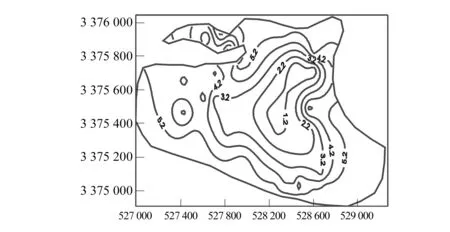
图19 模式3第三层垂向应变Fig.19 Strain contour in Layer 3 for case 3

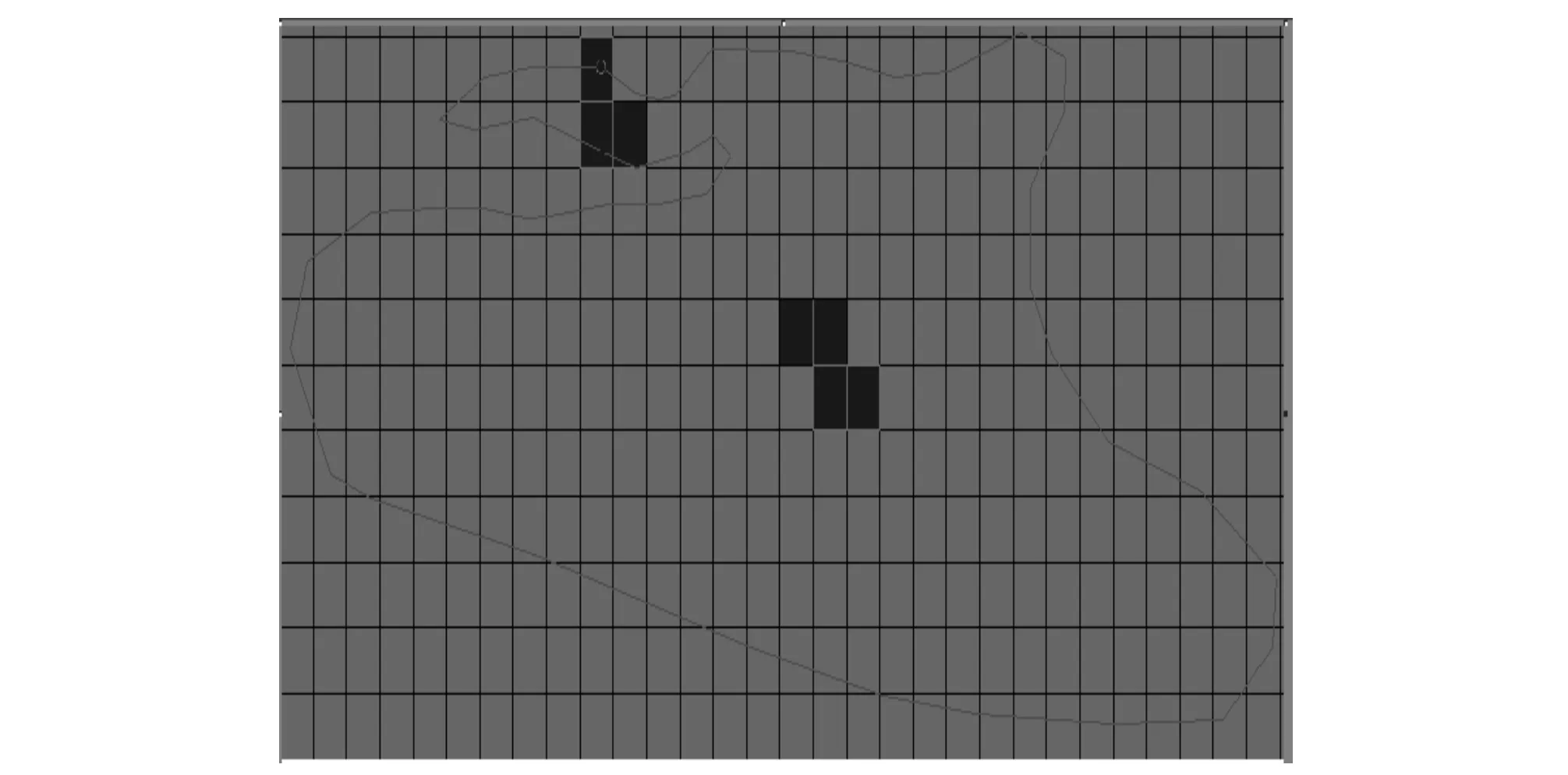
图20 模式3第三层破坏区Fig.20 Destroy zone in Layer 3 for case 3

模拟结果表明，研究区降雨对于土洞稳定性有明显影响。三种模式下应力分布规律大致相同，由于区内地下水与长江有着较直接的排泄途径，短期的降雨没有造成水位大幅度上升，但使水压力增大导致土洞破坏。由以上模拟分析的变形位移图可知，相同时间下，降雨强度越大，土洞变形越大，同时降雨强度较小但持续时间较长时，对土洞的影响几乎和降雨强度较大的暴雨相同，也可成为塌陷的主要诱发因素。

5 结 论

(1)基于地下水动力学理论和Terzaghi固结沉降理论，采用MODFLOW软件和自编Terzaghi模型计算程序，建立了青菱乡烽火村岩溶塌陷区地下水动力学-岩土力学耦合数值模型。

(2)利用该模型模拟了长江水位动态、基坑排水、降雨等因素对岩溶塌陷的影响，结果表明：长江水位上升、下降交替出现时，土体发生破坏且塌陷点偏移长江方向；周边工程建设排水施工时，降落漏斗最深处沉降量4 mm，对土洞的破坏性影响最大；降雨强度不大，但降雨时间长造成的土体变形大，最大处引起土体上浮1～2 mm，大大降低了盖层的强度。

□

[1] Lu Y R，Liu Q，Zhang F E，et al. Environmental characteristics of karst in China and their effect on engineering[J]. Carbonates and Evaporites，2013，28(1-2)：251-258.

[2] 郭殿权，刘道喜. 武昌陆家街地面塌陷成因机理分析[J].工程勘察，1990,(6):11-13.

[3] He K Q，Zhang S Q，Wang F，et al.The karst collapses induced by environmental changes of the groundwater and their distribution rules in North China [J]. Environmental Earth Sciences，2010，61(5):1 075-1 084.

[4] 胡亚波，刘广润，肖尚德,等.一种复合型岩溶地面塌陷的形成机理——以武汉市烽火村塌陷为例[J].地质科技情报，2007，26(1):96-100.

[5] 张人权，梁 杏，靳孟贵，等.水文地质学基础[M].6版.北京，地质出版社，2011.

[6] 方 云，林 彤，谭松林. 土力学[M]. 武汉: 中国地质大学出版社，2003.

[7] He K Q，Jia Y Y，Zhao M，et al. Comprehensive analysis and quantitative evaluation of the influencing factors of karst collapse in groundwater exploitation area of Shiliquan of Zaozhuang，China[J]. Environmental Earth Sciences，2012，66(8):2 531-2 541.

[8] Zhao H J，Ma F S，Guo J，et al. Regularity and formation mechanism of large-scale abrupt karst collapse in southern China in the first half of 2010[J]. Natural Hazards, 2012，6(3)：1 037-1 054.

[9] Liu X M，Chen C X. Prediction and evaluation of space collapse for typical covered karst[J]. Disaster Advances，2010，3(4): 120-126.

[10] He K Q，Jia Y Y，Wang B. et al.Comprehensive fuzzy evaluation model and evaluation of the karst collapse Susceptibility in Zaozhuang Region，China [J]. Natural Hazards，2013，68(2):613-629.

[11] Haijun Zhao o Fengshan Ma o Jie Guo. Regularity and formation mechanism of large-scale abrupt karst collapse in southern China in the first half of 2010[J].Natural Hazards，2012，60:1 037-1 054.