马斯京根汇流参数抗差估计研究

2016-03-22沈丹丹包为民刘可新龚婷婷陈伟东河海大学水文水资源学院南京210098

中国农村水利水电 2016年7期

沈丹丹，包为民，刘可新，龚婷婷，张乾，陈伟东(河海大学水文水资源学院，南京 210098)

0 引言

马斯京根汇流参数估计采用的是河段上下两断面的实测流量过程资料。若流量资料误差为服从零均值正态分布或对数正态分布的随机误差时，利用传统的估计理论(如最小二乘法)可取得比较好的估计效果；但当流量资料中存在异常值时，用传统的估计方法进行参数估计常常会得出不合理的参数估计结果[1]。

抗差最小二乘法将抗差理论与最小二乘法相结合，利用抗差理论的特性抵御异常误差对参数估计的影响，从而提高参数估计的精度和稳定性。本文将附有条件的抗差最小二乘法运用到马斯京根汇流参数估计中，利用闽江流域沙县河段21场实测入流资料构建理想模型，并基于人工生成的零均值正态分布的随机误差和异常误差这两类误差，分析检验了用抗差最小二乘法进行参数估计的有效性与稳定性。

1 参数估计方法

1.1 最小二乘法

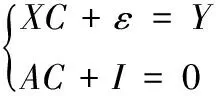
(1)

采用拉格朗日算子法，可导出最小二乘解：

(2)

1.2 附有条件的抗差最小二乘法

利用抗差等价权原理，采用拉格朗日算子法，可导出抗差最小二乘估计，为：

(3)

式中：W是对角元素为ωi的对角阵；ωi为抗差权函数。

根据文献[2]的研究，本文使用如下三段权函数和函数变量：

(5)

式中：ωi为抗差权；εi为权函数变量；k1和k2为待定的常数，本文中分别取1和2.5；Qi和Qci分别为下断面实测流量和计算出流；n为计算时段数。

1.3 抗差最小二乘法计算步骤

(1)由式(5)和式(4)分别计算出εi和ωi的值；

污水的深度处理工艺的目的是进一步去除污水中经二级处理后剩余的污染物质，工艺的选择取决于二级处理出水的水质和所需达到的水质标准。二级处理出水中污染物质为有机物和无机物的混合体，有机物包括细菌、病菌、藻类及原始生物等。不论是有机物还是无机物，根据它们存在于污水中的颗粒的大小又可分为悬浮物（＞1μm）、胶体（1μm ～1nm）和溶解物（<1nm），一般来说通过混凝沉淀等常规工艺可以去除悬浮物和胶体粒子。溶解性杂质必须通过某些非常规手段才能去除。

(2)计算等价权矩阵W；

2 应用实例

2.1 理想系统设计

本研究采用的汇流参数为C0=0.27，C1=0.50，C2=0.23，上断面入流过程选用了闽江流域沙县断面1989-2001年21场不同量级和不同特点的实测洪水过程(21场洪水的洪峰流量和最小流量见表1)，并用式(1)计算相应的下断面的出流过程作为理想系统的输出。由此构成的理想模型的参数、输入和输出都是已知且无任何误差。

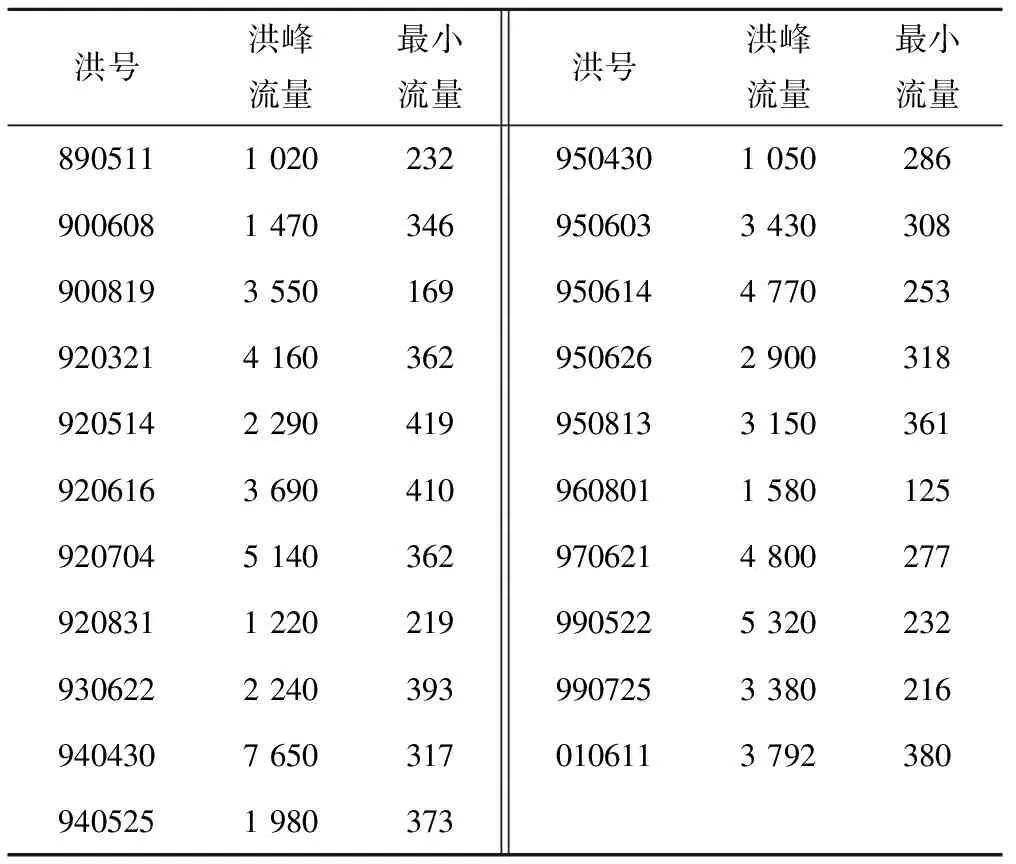
表1 21场洪水的洪峰流量和最小流量值 m3/sTab.1 The peak discharge and the minimum discharge of 21 floods

2.2 误差生成

观测误差按绝对值大小分一般可分为小误差、粗差和极值误差。小误差发生频率高，且一般服从零均值正态分布或对数正态分布；而粗差和极值误差发生频率低、变化较大，一般不具有这些误差统计特征。因此，本文采用如下两种误差生成模式：

δi～N(0,var)i=1,2,…,n

(7)

3 结果分析

3.1 随机误差

在1.1构建的理想模型的下断面计算出流过程上加上式(6)生成的随机误差，分别用最小二乘法和抗差最小二乘法估计河段马斯京根汇流参数，估计结果如表2。表2中Cl0，Cl1，Cl2为最小二乘法估计的汇流参数；Cr0，Cr1，Cr2为抗差最小二乘法估计的汇流参数。随机误差情况下两种估计方法的汇流参数估计结果(以参数C0为例)统计如图1。

表2 随机误差的参数估计结果Tab.2 Parameter estimation results of random errors

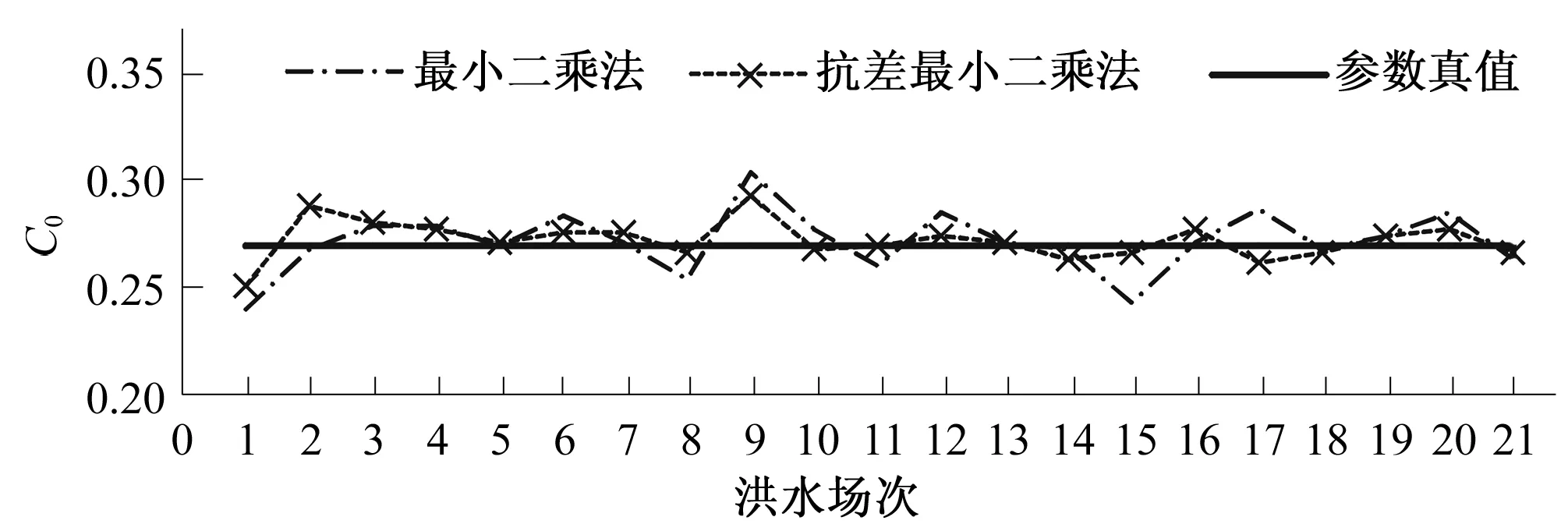
图1 随机误差参数(以C0为例)估计结果图Fig.1 Parameter estimation results of random errors(take C0 as example)

分析表2可以发现，当实测资料的观测误差服从零均值正态分布时，用最小二乘法和抗差最小二乘法估计出的参数值相差不大，且都非常接近真值。但比较而言，最小二乘法估计的参数均值更接近真值，说明此时最小二乘法的估计效果更好。

参数估计均方差从统计意义上反映了参数估值对于参数均值的偏离程度。因此，在同样的样本资料条件下，两种不同方法的参数估计均方差可以反映两种评价方法的稳定性。从表中可以看出，最小二乘法和抗差最小二乘法的参数估计均方差都比较小，表明误差服从零均值正态分布时，两种方法估计结果都比较稳定。但比较而言，抗差最小二乘法的参数估计均方差更小，因此，抗差最小二乘法估计结果更稳定。

由图1参数估计结果统计图也可以看出，随机误差情况下，两种方法的估计效果和稳定性相差无几，与表2分析结果相吻合。

综上所述，当误差服从零均值正态分布时，两种方法的参数估值都是有效的。最小二乘法估计结果更接近真值，而抗差最小二乘法的估计结果更稳定。

3.2 异常误差

在理想模型的下断面计算出流过程上加上式(7)生成的异常误差，这里时间间隔L取10 h，即本文采用的是崩溃率为10%的误差资料。分别用最小二乘法和抗差最小二乘法估计河段马斯京根汇流参数，估计结果如表3。表3中Cl0，Cl1，Cl2为最小二乘法估计的汇流参数；Cr0，Cr1，Cr2为抗差最小二乘法估计的汇流参数。异常误差情况下两种估计方法的汇流参数估计结果(以参数C0为例)统计如图2。

由表3可以发现，当误差为不满足正态分布的粗差或极值误差时，虽然最小二乘方法估计结果的均值与真值很接近，但每场洪水的参数估值都严重偏离真值，例如890511号洪水，最小二乘估计的参数估值为0.040 4，0.716 4和0.243 2。此时，最小二乘估计方法几近崩溃，根本无法得出有效的参数估值。而抗差最小二乘法的估计结果，无论从次洪还是估值的均值来看都非常接近真值，且参数估计均方差较小，稳定性较好。说明，在异常误差的情况下，抗差最小二乘法利用抗差特性抵御了异常值对参数估计的影响，能够获得有效且稳定的估计结果。

分析图2可以发现，异常误差情况下，最小二乘法估计结果严重偏离真值，且上下波动非常大，估计结果极不稳定；而抗差最小二乘法参数估值与真值非常接近，且稳定性较好。这与表格分析结果一致。