井渠灌区地下地表水耦合模拟及用水配置研究

孙骁磊，田军仓，朱 磊(1.宁夏大学土木与水利工程学院,银川 750021;2.宁夏节水灌溉与水资源调控工程技术研究中心，银川 750021;3.旱区现代农业水资源高效利用教育部工程研究中心，银川 750021)

井渠结合灌区具有充分利用地表水地下水、循环利用灌溉及渠系渗漏水、适时调控灌区地下水位、防治土壤发生次生盐碱化、能够实现适时灌溉、提高水资源利用率等突出特点，是我国西北地区灌区实现农业高效用水不可或缺的组成部分[1]。

2008年，宁夏水利厅确定了惠农渠、唐徕渠、汉渠3个典型引黄自流灌区试点，实施井渠结合灌溉综合规划，总灌溉面积达到0.262万hm2，机井分布达223眼。2010年，井渠结合的灌溉面积，平均已达到1万hm2规模，机井布置达到600眼左右[2]。但因当地农户反应井水凉、地下水矿化度较高使土壤积盐等问题，人工开采进行井灌积极性不高。尤其在作物需水量较大的六七月份，黄河来水较充沛时期，机井大多处于闲置或者弃用的状态，甚少用井水，破坏了地下水的采补平衡。只有在黄河水枯竭和断流时期进行井水补灌。人工开采数量相对较少，使得地下水埋深超过适宜的埋深临界。因此分析地下水-地表水水分相互转化关系，确定适宜的地下水-地表水配水比是迫切需要解决的问题。

针对地下水-地表水的联合耦合模拟，国内外不少学者开展了大量的工作。张浩佳，吴剑锋等，通过降雨径流的模拟系统PRMS和三维有线差分模型MODFLOW提出地下水-地表水GSFLOW模型，提出不同水文参数对于流域水资源影响提供理论和技术支撑[3]。Kim等针对SWAT模型在地下水及MODFLOW模型在地表水上模拟的不足，对SWAT模型优先进行输参，得到的结果由MODFLOW运行，输出后的结果最后由SWAT进行计算。得到的模型能够较全面的模拟地下水的补排规律以及地表水地下水的相互作用[4]。刘路广，崔远来等，通过将SWAT和MODFLOW中的差分网格进行相互对应，对改进的SWAT模型每个HRU地下水补给计算数值，再通过HRU-cells界面作为MODFLOW地下水模型补给板块的输入项，完成了试验灌区地下地表水分布式模型耦合[5]。曾献奎针对凌海市大、小凌河扇地内的水文地质条件，采用HydroGeoSphere软件建立试验灌区地下水-地表水水流运动及溶质运移耦合的模拟模型，选择总氮作为模拟对象，对研究区的水流及总氮浓度进行模拟分析与预测，并对当地水资源管理与规划提出建议[6]。

地下水地表水耦合模拟已经趋于完善，但是目前国内利用HydroGeoSphere软件对灌区地下水地表水进行耦合模拟的研究较少，并且通过耦合模拟对引黄灌区适宜地下水埋深进行探讨的相关研究就更少。因此本文通过建立地下水-地表水耦合模拟模型，运用HydroGeoSphere 对模型进行计算求解，并通过建立的地下水模拟模型，调整用水比例，对研究区内的地下水动态变化进行预测分析，得到在生态安全埋深下，渠井用水最优比例。

1 材料与方法

1.1 研究区概况

本文研究以宁夏银北引黄灌区为背景，试验灌区位于宁夏回族自治区惠农区李岗村试验区，东经106°～107°E，北纬38°～40°N之间， 海拔1 091.0 m，地处宁夏引黄灌区，东临黄河，西倚贺兰山，总控制面积212.4 hm2，耕地面积143 hm2，试验灌区的主要种植作物为小麦和玉米，以及西瓜、芹菜、番茄等经济作物，作物生育期总灌溉水量42.373 7 万m3，总抽水量10.307 2 万m3，现状年下渠首引水量水和抽井水量的用水比例接近4∶1。

试验区砂砾石分布广泛，灌区土壤的质地主要为沙壤土和壤土两种，耕作层的土壤干密度为1.45 g/cm2，土壤全盐量0.48～0.93 g/kg，适合农业耕作。试验区东部边界为官泗渠，西、南、北分别为第五排水沟、蔡家沟、艾家沟。试验区共有抽水井19眼，农渠39条，黄河来水在每年的4月底-8月底时期。

1.2 研究内容与方法

本次研究采用田间勘测与数值计算结合的方式进行开展，研究宁夏银北井渠结合灌区地表水与地下水水分运移规律。试验灌区内共设置6眼地下水位的观测井，试验观测内容主要为：大气观测、田间灌溉水量、灌区排水量观测以及地下水的动态变化观测。观测井具体布置见图1。

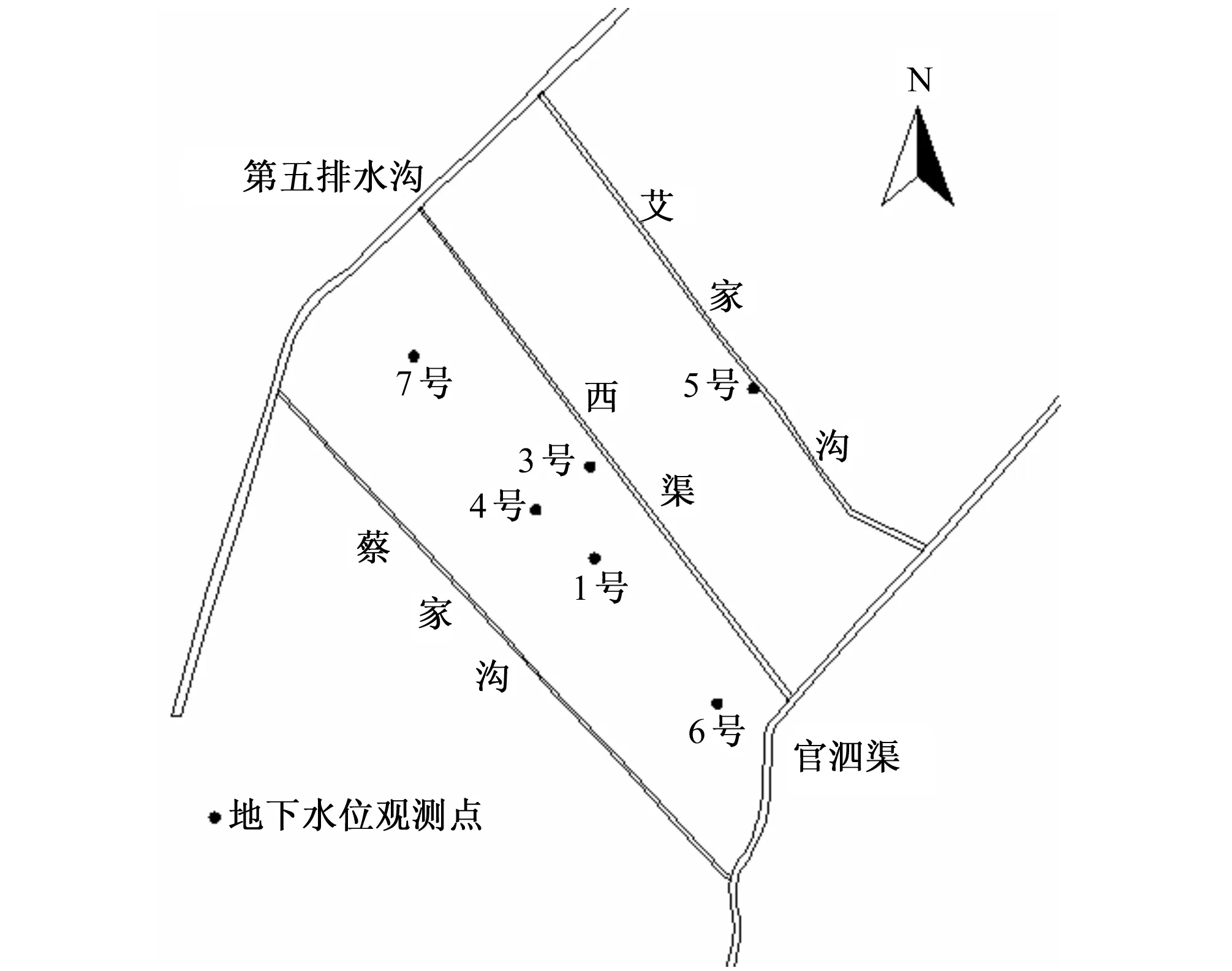
图1 试验灌区观测井的平面布置图Fig.1 Test area observation wells

2 地下水-地表水耦合模拟

2.1 水文地质概念模型

试验灌区属贺兰山山前坳陷，地下水埋深较浅，地下水开采主要以潜水为主，含水层为单一的潜水层，潜水层以下的亚沙土、亚黏土、黏土部分作为相对隔水底板[7]。承压水层一般的埋深在60 m以下，为远源的补给水，本灌区不作为灌溉用水水源。因本试验区地下水的开采未深入到承压水含水层，所以本次模拟以潜水为主。

尽管试验灌区地下水运动以垂向为主，水平方向上几乎无流动，试验区农沟较多，一部分地下水先通过各农沟汇入南北两侧斗沟(艾家沟和蔡家沟)，再由南北的斗沟排泄到西部的第五排水支沟排出。所以在概化潜水含水层的侧向边界条件时，将南北边界，即艾家沟和蔡家沟，其主要作用为侧向排水，设定为第二类边界。西部边界即第五排水支沟，其主要作用为侧向排水，设定为第二类边界。试验区东部为官泗渠，概化为河流边界。研究区内的地表水系统的源汇项主要有大气降雨补给、灌溉入渗补给、蒸发蒸腾、人工开采等。

2.2 数学模型

2.2.1地下水水流数学模拟模型

根据研究区水文地质模型，采用三维Richards方程定解条件及初始条件来描述研究区饱和、非饱和地下水的非稳定运动，建立相应的数学模型如下[8,9]：

(1)

q=-Kkr▽(ψ+z)

(2)

式中：q为地下水的渗流量；QGS为地表水入渗量；QG为地下水流的源汇项；Sw为饱和度，无量纲；Ss为贮水系数；ψ为压力水头；θs为饱和含水率(近似等于孔隙度)，无量纲；Ho为边界上水头；Γ1、Γ2和Γ3分别为给定水头边界、零通量边界和给定流量边界；qG为边界上的水流通量；Ω为试验区的地下水区域；K为渗透系数张量；kr为相对渗透率，无量纲；z为位置水头。

通过van Genuchten公式得到相对渗透率kr：

(4)

式中：Se为有效含水量，无量纲；Swr为残余含水率，无量纲；α为空气负压；β为孔隙大小的分布指数，无量纲；lp为孔隙连通性参数，无量纲。

2.2.2地表水水流数学模拟模型

研究区内的地表径流受到微地形的影响，其运动属于缓变不稳定的波动。所以采用忽略动量项的二维圣维南方程组(二维浅水方程)描述地表径流运动[6,8,9]。

(5)

式中：φo为地表孔隙度，无量纲；ho为水面高程；Kox、Koy为x、y方向上的地表传导系数；Qo为地表水的源汇项；do为地表径流深度；Do为地表水范围；h(x,y,t)为给定水深第一类边界条件；qo1(x,y,t)为给定通量的第二类边界；Kn为边界法向的地表传导系数张量；qo2(x,y,t)为临界深度边界条件；qo3(x,y,t)为零深梯度边界条件；So为地表坡度，无量纲；h(x,y,0)为初始条件。

Kox,Koy可由下式求出：

(6)

式中：nx和ny分别是x和y方向上的曼宁糙率系数。

2.2.3地下水-地表水水流数学模型的耦合

本次研究所采用的软件HydroGeoSphere采用双重节点法，从物理机制上将地下水和地表水进行耦合处理，进行模型的耦合时，首先将二维平面地表水模型重叠在地下水模型的顶部，对地下水、地表水模型进行相同的空间和时间的离散。将试验区剖分为31 080个节点和54 648个单位，并选择2015年3月27日-7月4日(共100 d)作为耦合模拟的率定期，2015年7月5日-10月12日(共计100 d)作为耦合模拟的验证期。本次模拟的时间步长输出为1 d。

试验区表层的地表水模型的节点与地下水模型的顶部节点获得相同的空间坐标，也就是说耦合模型表层的节点兼有地表水和地下水的双重属性，将上下层节点同时进行水力联系。在模型中地表水与地下水体间的水头保持完全相同，在模拟的过程中，以方程整合的方式对地表水与地下水量以及两者之间的交换进行水力计算[6,8,9]。

在这样的耦合方式下，并不假设相互系统间水头的连续性，水流交换的描述是通过达西流关系来实现：

dQGS=kroKso(h-hs)

(7)

式中：d为地表水与地下水的耦合的长度；QGS为地下水和地表水的通量交换;kro为上游节点的相对渗透率，无量纲；Kso为地下水的表层介质渗透系数;h为地下水水头；hs为地表水水头。

2.3 模型的率定与检验

2.3.1模型的率定

本文将试验区在竖直方向上划分为23层，根据抽水井的实际分布情况，以19眼抽水井平均分配的原则将试验区划分为六块平面区域建立模型(见图2)，利用GRIDBUILDER对试验区二维平面区域图进行前期处理，再进行网格剖分，在边界处及边界排水处，采用栅格加密进行描述(见图3)。

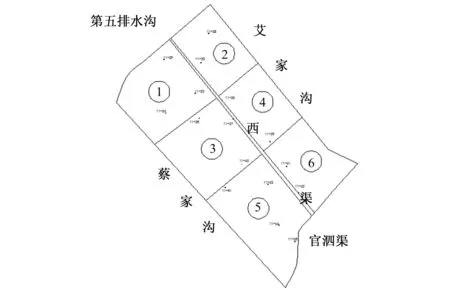
图2 试验灌区平面区域划分图Fig.2 Flat test area zoning

图3 试验灌区模型栅格剖分图Fig.3 Experimental zone model meshing figure

试验灌区的水文地质参数的初始值主要通过前人的研究资料并结合实际问题得出[10,11](见表1)。选择2015年3月27日-7月4日(共100 d)，作为模拟的率定期，确定模型的时间步长输出为1 d。为验证所选取的水文地质参数的真实性和所建立的数学模型的可靠性，在研究区内对已布置的6眼潜水观测井进行观测，利用实际观测得到的地下水动态变化资料来对模型进行率定。试验灌区空间离散图，如图4所示。

表1 主要水文地质参数的取值Tab.1 The main values of hydrogeological parameters

2.3.2模型的验证

为了进一步验证上述建立的模型的可靠性，选取2015年7月5日-10月12日(共计100 d)的地下水位动态观测资料对模型进行验证，试验区率定期和验证期各观测井地下水埋深变化实测值与计算值如图5所示。1号井、2号井、4号井、6号井种植作物为玉米，玉米全生育期灌溉3次，所列观测井渠井灌水时间较统一，即5月中后旬到9月中旬为地表径流与地下水水分相互交换的激烈期，明显看到有3次上升和3次下降。5月初到6月中旬，灌溉的补给是导致地下水位的上升的主要原因，在这个阶段，地下水量的消耗相对较少，地下水位上升约0.9 m。6月初到9月初，受到田间灌溉、大气降雨以及潜水蒸发等因素的影响，地下水水位呈波动性变化，但总体呈现出缓慢下降的趋势，下降约0.6 m。这说明，地下水的消耗不仅仅有灌区人工开采的原因，也表明作物在生育期内要消耗了一部分地下水，地下水是作物需水的不可或缺的一部分。

图4 试验灌区模型空间离散图Fig.4 Discrete model space test area

图5 率定期与验证期内地下水埋深的实测值与模拟值对比Fig.5 Comparison of measured and simulated values of groundwater level at regular and verification stages

从图5可以看出，经率定之后的模型在验证期内计算出的地下水埋深与实测值的变化趋势较为统一，模型计算得到的地下水埋深与地实际观测埋深的绝对误差小于0.2 m的时间天数占总观测天数的90%以上。表明模型所选择的含水层结构、概化得到的边界条件以及水文地质参数的选取合理。同时试验灌区的地下水系统特征能够通过所建立的数学模型真实地刻画得到，模型用来对试验灌区的地下水埋深进行预测是真实可靠的。

图6为模型进行计算后试验区不同时期饱和度的分布图，其中云图表示饱和度的大小。图6表示了在各个时期土壤水流饱和度的发展。从图6可以看出，在模拟初期及3月末4月初，试验区未进行灌溉，部分区域只以单井进行少量的灌溉，试验区水位较低，各观测井地下水埋深达到2 m以下，饱和度在0.69～0.76之间不断变化。在七八月试验区机井基本处于闲置状态，但渠灌溉水量为最大时期，试验区地下水位不断升高，饱和度不断变大。在灌水期水量达到顶峰时期，即地下水埋深小于1 m不断靠近地表面时，饱和度垂向变化剧烈，灌水后饱和度最高达到0.9～0.96。进入九十月份，灌溉停止，土壤水流饱和度不断降低到0.68以下，水位不断下降至最低点达到2.2 m以下，验证期末时段地下水的三维水位图见图7。

图6 试验灌区不同时期饱和度分布图Fig.6 The saturation distribution of the test area in different periods

图7 验证期末时刻(2015-10-12)试验区地下水三维水位图Fig.7 Verification of the final time (2015-10-12) test area groundwater three-dimensional water level

3 基于耦合模型的最优渠井用水比例计算分析

试验灌区地下水与地表水相互联系密切，灌区内渠引水量和井抽水量及渠井配水比对灌区内地下水埋深的动态变化影响大，且试验灌区人工开采灵活，井灌设施配套齐全，通过改变渠井用水比，得到适宜的地下水埋深是切实可行的。

在不超过试验灌区渠引水量和地下水安全开采量的条件下，渠井的用水比例不宜过大，过大会引起地下水位上升，潜水无效蒸发增加，水资源重复利用率低，引起土壤次生盐碱化；渠井用水比例也不宜过小，过小会造成地下水严重超采，导致地下水漏斗[12,13]。

基于上述提出的地下水模拟，针对现状年渠井比例，进行调整，对试验区地下水埋深进行模拟预测。在现状年4∶1下，不断减小渠井用水比例，试验区各模拟情景及计算结果见表2。

表2 试验区各模拟情景设置下计算结果Tab.2 Calculation results under different simulation scenarios in the test area

由上述不同情景设置下计算结果表明：①在保证总用水不变的情况下，渠井用水比例不断减小对缓解地下水水位上升有明显的效果。通过情景1和情景5的对照分析，渠井用水比为3∶1下的渠首有效引水量比渠井用水比为2∶1下的渠首有效引水量减小了11.4%，地下水位下降近22.5%，地下水位平均下降约0.38 m。情景5与现状年相比，试验区减少渠首引黄量7.678 280 万m3，每公顷每年减少引黄量约361.35 m3/hm2，地下水水位下降0.4 m。②随着渠井用水比例的不断减小，由3∶1减小到2∶1的过程中可以看出，观测井地下水埋深的最小值也在不断增大(见图8)，由渠井用水比3∶1下的1.134 m减小到渠井用水比2∶1下的1.808 m，地下水埋深下降达到60%，下降0.674 m。得到在增加地下水的开采比例后，对地下水位的下降有一定的促进作用。③通过上述提出的符合宁夏引黄灌区生态安全的适宜地下水埋深，并结合上述情景计算结果，可以得到，在渠井比为2：1下的地下水埋深时，模型计算结果表明地下水最小埋深为1.808，平均埋深为2.074，符合上文提出的地下水埋深维持在1.8～3.0 m的范围。该情景下，即2∶1的渠井用水比可以适度缓解地下水补排失衡，模拟期间，地下水位变幅变化较稳定，人工调蓄有效措施控制地下水位持续上升，能够避免危害性的地质灾害现象发生。

图8为不同的渠井用水比例下，利用模型进行预测分别计算不同渠井用水比例下地下水埋设变化情况。

图8 不同渠井用水比例下地下水埋深变化Fig.8 Variation of groundwater depth under different water use ratio

由图8可得适当减小渠井用水比例，以井补渠，可以得出黄河引水量减少明显，同时适当加大开采地下水量，能够保证地下水仍处在适宜埋深。

4 结 语

(1)在分析概化宁夏惠农李岗村试验区水文地质的基础上，采用双重节点方式对地表水模型与地下水模型进行耦合，并通过HydroGeoSphere软件对耦合模型进行计算计算求解。全面分析了试验区灌水期地下水系统输入输出的转化关系，在三四月以井灌为主时期，地下水开采量较大，并且处于集中开采期，地下水水位的下降幅度变化较大，地下水平均埋深在2 m左右，饱和度在0.69～0.76之间变化。七八月份为渠灌水量最大时期，地下水水位明显升高，地下水埋深最高达到1 m，超过生态安全水位，部分水位较高地区饱和度上升到0.94～0.96。当九十月份渠首停止引水后，地下水位又重新下降，最低达到2.2 m左右，饱和度下降到0.68以下。

试验区灌水期地下水地表水水分变化规律为当地地下水资源的合理开发和科学管理提供了依据。

(2)结合地下水地表水耦合模拟模型，得出在不同情景设置下，即不同渠井用水比例下地下水埋深的变化情况。计算结果表明，引黄灌区目前渠井灌水比例在4∶1左右，地下水平均埋深接近1.5 m，越过生态安全水位。建议试验灌区渠引水量与井抽水量比例控制在2∶1，试验区减少渠首引黄量7.678 280 万m3，每公顷每年减少引黄量约361.35 m3/hm2，节水效果明显，且地下水埋深能够维持在1.8～2.6 m的适宜安全埋深范围内。

[1] 史海滨，田军仓，刘庆华.灌溉排水工程学[M]. 北京：中国水利水电出版社，2006：210-216.

[2] 马德仁，刘学军. 宁夏井渠结合灌区管理技术研究与实践[J].人民长江，2014，45(14):107-111.

[3] 张浩佳，吴剑锋，林 锦，等. 基于GSFLOW 的地下水-地表水耦合模拟与分析[J].工程勘察，2015，43(5):34-38.

[4] Kim N W，Chung I M，Won Y S, et al. Development and application of the integrated SWAT-MODFLOW model [J]. Journal of Hydrology, 2008,356:1-16.

[5] 刘路广，崔远来.灌区地表水-地下水耦合模拟的构建[J].水利学报，2012，43(7):826-833.

[6] 曾献奎. 基于HydroGeoSphere的凌海市大、小凌河扇地地下水-地表水耦合数值模拟研究[D]. 长春：吉林大学，2009.

[7] 席文娟.宁夏石嘴山地区地下水水质模拟与变化趋势分析[D].西安：长安大学,2013.

[8] 朱 磊，田军仓，孙骁磊.基于全耦合的地表径流与土壤水分运动数值模拟[J].水科学进展，2015，26(3):322-330.

[9] R Therrien，R G McLaren, E A Sudicky, et al. HydroGeoSphere: a three-dimensional numerical model describing fully-integrated subsurface and surface flow and solute transport[R]. Waterloo: University of Waterloo, 2009.

[10] 刘玉珍. 平原区地下水系统模拟与决策支持研究[D]. 辽宁大连：大连理工大学, 2008.

[11] Marcel G S, Feike J L. Improved prediction of unsaturated hydraulic conductivity with themualem-van Genuchten model [J]. Soil Science Society of American Journal, 2000,64:843-851.

[12] 周维博，李佩成.井渠结合灌区节水灌溉的有效途径[J].沈阳农业大学学报, 2004,35(5-6):473-475.

[13] 樊自立，陈亚宁，李和平，等．中国西北干旱区生态地下水埋深适宜深度的确定[J].干旱区资源与环境，2008，22(2):1-5.