最短路径距离矩阵修正的多维标度定位算法

任克强，庄放望（江西理工大学信息工程学院，江西赣州341000）



最短路径距离矩阵修正的多维标度定位算法

任克强*，庄放望
（江西理工大学信息工程学院，江西赣州341000）

摘要：为了减小最短路径距离矩阵与欧氏距离矩阵之间的差异，提高MDS-MAP（C）算法的节点定位精度，提出一种改进的多维标度节点定位算法。该算法对MDS-MAP（C）算法进行了以下改进：采用启发式的搜索策略对最短路径距离矩阵进行修正，以减少最短路径距离矩阵与实际的欧氏距离矩阵之间的误差；利用smacof算法迭代误差函数代替SVD分解来求解节点的定位问题，以优化和改善节点定位的求解过程。实验结果表明，与MDS-MAP（C）算法相比，改进算法能够减少最短路径距离的误差，有效提高节点的定位精度，并且对不规则网络具有更好的适应性。

关键词：无线传感器网络；最短路径；MDS-MAP（C）算法；节点定位；多维标度；smacof算法

无线传感器网络WSN（Wireless Sensor Net⁃work）由大量部署在监测区域内的廉价微型传感器节点构成，它是一种自组织、分布式处理以及快速展开的无线网络［1］。传感器节点的位置信息对WSN的监测活动极其重要，获取准确的传感器节点位置信息是WSN进行相关监测以及传感器节点进行下一步活动和决策的基础［2］。WSN的节点定位算法按定位机制的不同可分为基于测距（Rangebased）的算法和测距无关（Range-free）的算法［3-4］。Range-based算法通过测量节点之间的距离或角度来实现定位，Range-free算法则无需测量节点之间的距离和角度信息，而是根据网络的连通性等信息来实现定位［5］。Range-based的代表算法有基于到达时间TOA（Time of Arrival）的定位、基于到达时间差TDOA（Time Difference of Arrival）的定位、基于接收信号强度指示RSSI（Received Signal Strength Indi⁃cator）的定位以及基于到达角度AOA（Angle of Ar⁃rival）的定位等算法［6-8］。Range-free的代表算法有距离向量-跳段DV-hop（Distance Vector-hop）定位、凸规划（Convex Optimization）定位以及多维标度MDS（Multidimensional Scaling）定位等算法［9-10］。

MDS是一种将多维空间中的研究对象简化到低维空间中进行定位、分析和归类，并且保持研究对象之间原有关系的多元数据分析技术。Shang Yi等人将MDS技术应用于WSN的节点定位，提出了MDSMAP算法［11］；该算法利用节点间的连通性或距离估计信息进行定位，将节点间最短路径距离近似为节点间的欧氏距离，再利用MDS方法进行定位；当网络拓扑不规则时，由于最短路径距离与节点间实际的欧氏距离相差较大，严重影响算法的定位精度。为了解决最短路径距离与节点间实际欧氏距离的差异性问题，国内外研究人员提出了不同的MDS-MAP算法改进和优化方案。文献［12］将网络拓扑分解为多个局部地图，再按分布式的计算模式对局部地图进行MDSMAP定位，减少了最短路径距离与节点间实际欧氏距离的误差，但在Range-Free环境的定位精度依然不高。文献［13］在生成相对地图的过程中采用迭代更新的方式来改善定位性能，使其定位精度有了较大的提升，但计算复杂度较高，节点的能耗较大。文献［14］采用距离矩阵重构的方式来替代最短路径距离矩阵，并用奇异值分解SVD（Singular Value Decompo⁃sition）低秩近似的方法来求解距离矩阵。文献［15］提出基于距离矩阵重构的WSN多维标度定位算法，利用节点间的相关信息对距离矩阵进行线性重构，然后使用经典MDS进行定位，取得了较好的定位精度。文献［16］针对MDS-MAP在不均匀网络中定位精度较低的问题，提出一种可用于不均匀网络的节点定位算法，有效地减小了平均定位误差。文献［17］提出改进距离重构的三维节点定位算法，该算法利用MDS-MAP算法获取节点之间相对的坐标，并采用精度更高的坐标映射方案对坐标转换过程进行优化，取得了较高的三维节点定位精度。

针对最短路径距离与节点之间实际欧氏距离的差异性问题，本文提出一种基于最短路径距离矩阵修正的多维标度定位算法MDS-DMC（MDSDistance Matrix Correction），通过修正最短距离矩阵来逼近欧氏距离矩阵，以提高节点的定位精度。

1　多维标度定位算法

MDS-MAP（C）是一种基于经典MDS（Classical MDS，CMDS）的多维标度定位算法，该算法将各个节点视作一个实体元素，各节点之间的相似性用欧氏空间距离来表示，通过建立欧氏空间距离与相似性信息的线性映射关系后，就可在多维空间内获得节点的分布。如果获得的相似性信息与欧氏空间距离的差异不大，则利用CMDS就可得到各节点之间相对的位置空间分布。

令Pi，j为m维空间中i和j两个点的相似性信息，通常等价于欧氏空间距离di，j，i点坐标为xi=(xi1，xi2，…，xim)，j点坐标为xj=(xj1，xj2，…，xjm)，则：

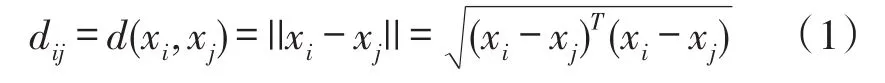
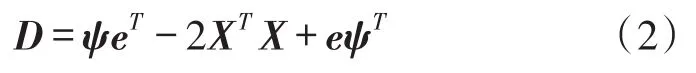
其中，e为元素全1的N×1维向量。

定义中心矩阵H=I-eeT/N（I为单位矩阵），对D进行双中心化：

2　MDS-DMC算法

MDS-MAP（C）算法以节点之间的最短路径距离替代欧氏空间距离，并采用SVD分解求解节点位置。在密集且分布均匀的网络环境中，最短路径距离可以近似欧氏空间距离；但在稀疏且分布不均的网络环境中，最短路径距离与欧氏空间距离的差异往往很大，此时两者近似将产生较大的误差。此外，当网络规模很大时，采用SVD分解求解节点位置比较复杂且定位精度不高。本文针对这些问题，提出MDS-DMC算法，对MDS-MAP （C）算法进行了两个方面的改进：①采用启发式的搜索策略对最短距离矩阵进行修正，以减少最短距离矩阵与实际的欧氏距离矩阵之间的误差；②使用smacof算法迭代误差函数代替SVD分解来求解定位问题，以改善和优化节点定位的求解过程。

2.1最短距离矩阵的修正

假定节点所能辐射范围的通信半径为R，A、C两个节点之间的距离L无法直接获取，如图1所示。

如果用最短路径算法求取的最短路径距离来近似代替A、C节点之间的距离L，则有AC≈AB+BC，即L≈d1+d2。

很明显，这种近似存在误差。为了减少误差，本文通过以下启发式的搜索策略来修正最短距离矩阵。

根据余弦定理，有：

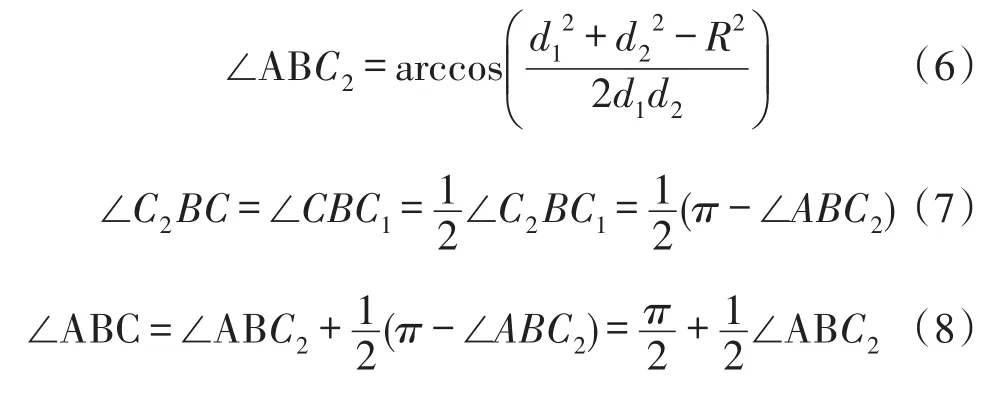
由上可得：

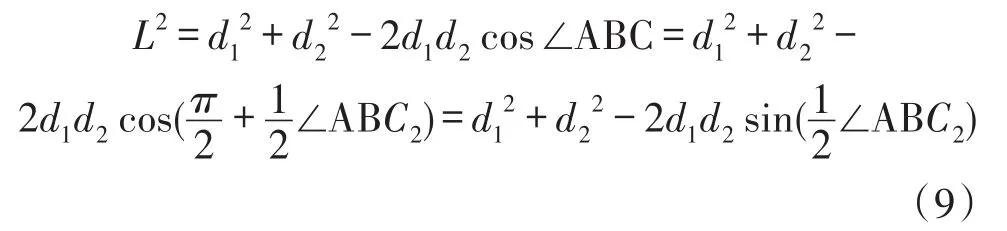
因此，通过以上方法修正最短距离矩阵，可以改善用最短距离矩阵近似欧氏距离矩阵产生的误差。

2.2求解节点位置的改进

对于节点数目为N的网络，使用SVD分解求解节点位置的复杂度为O(N3)，当节点规模很大时，一般采用迭代的方法代替SVD分解，以提高求解节点位置的效率。本文采用Metric MDS求解节点的位置，并利用smacof算法迭代误差函数代替SVD方法求解节点的定位问题，以下简称为MDS-MAP （smacof）算法。

定义函数S作为估算距离与实际距离的误差函数：

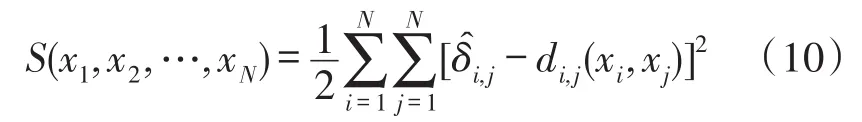
将式（10）展开得到：

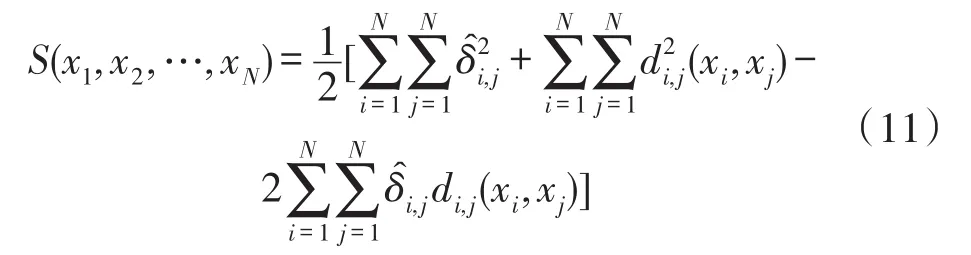
将式（11）转化成矩阵形式：

其中，trace{∙}为迹运算，代表矩阵的对角线元素之和；X是由所有节点组成的矩阵[x1，x2，…，xN]，XT是X的转置；H为中心矩阵，H=I-eeT/N，I为单位矩阵；Ψ(X)是关于X的中心矩阵，其元素由式（13）组成：

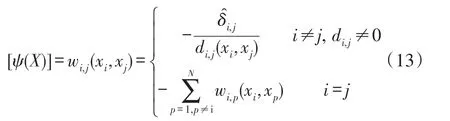
采用smacof算法，定义辅助函数φ(X，Z)为：

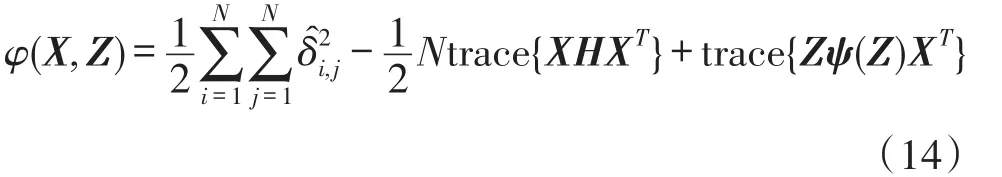
每次迭代k，采用Z=Xk-1，由于φ(X，Z)的梯度函数为：

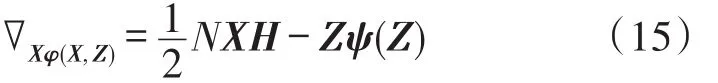
令梯度为0，可以得到：

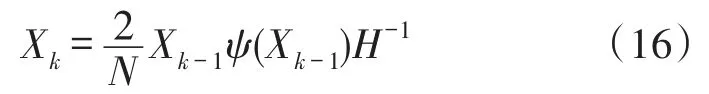
根据矩阵H的特性，可以推导出X的迭代形式：

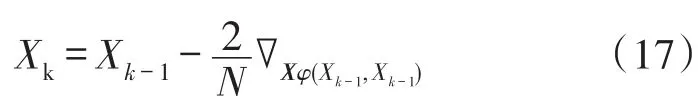
从而，节点的坐标可通过迭代的方式求得。

分析式(17)的迭代公式，求解该递归过程的复杂度为O(N2)，即节点坐标求解过程的复杂度为O(N2)；而执行SVD分解求解节点位置的复杂度为O(N3)。因此，通过smacof算法可有效降低求解节点位置的复杂度。

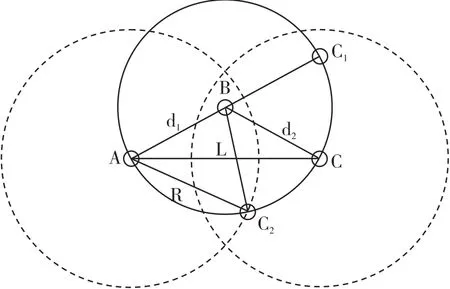
图1　最短距离矩阵修正示意图

3　实验结果及分析

为了测试MDS-DMC算法的改进效果，本文对MDS-MAP（C）算法、MDS-MAP（smacof）算法和MDSDMC算法进行了仿真比较实验。实验平台：WIN⁃DOWS XP SP3+MATLAB 2009a。实验环境与场景：矩形随机网络、C型随机网络；2-D平面L×L的区域内随机分布300个节点，包括4个锚节点。实验参数：未知节点通信半径为r，锚节点通信半径为R，并且r=R。

使用归一化的平均定位误差来评价实验算法的性能：

其中，N为网络节点个数，M为锚节点个数，r为未知节点通信半径，xi为节点i实际位置，为节点i估计位置。

3.1理想传输模型下的定位

该实验主要比较三种算法在理想传输模型的不同网络拓扑下的性能。在实验场景的两种网络拓扑下，随机部署300个节点，在通信半径为0.2 L的情况下，矩形网络平均连通度为31.1，C型网络平均连通度为34.6，分别用MDS-MAP（C）算法、MDS-MAP（smacof）算法和MDS-DMC算法进行定位。该实验的节点分布以及定位误差如图2~图4所示，图中空心圆圈代表未知节点的坐标，实心圆圈代表锚节点的位置，线段代表定位误差。

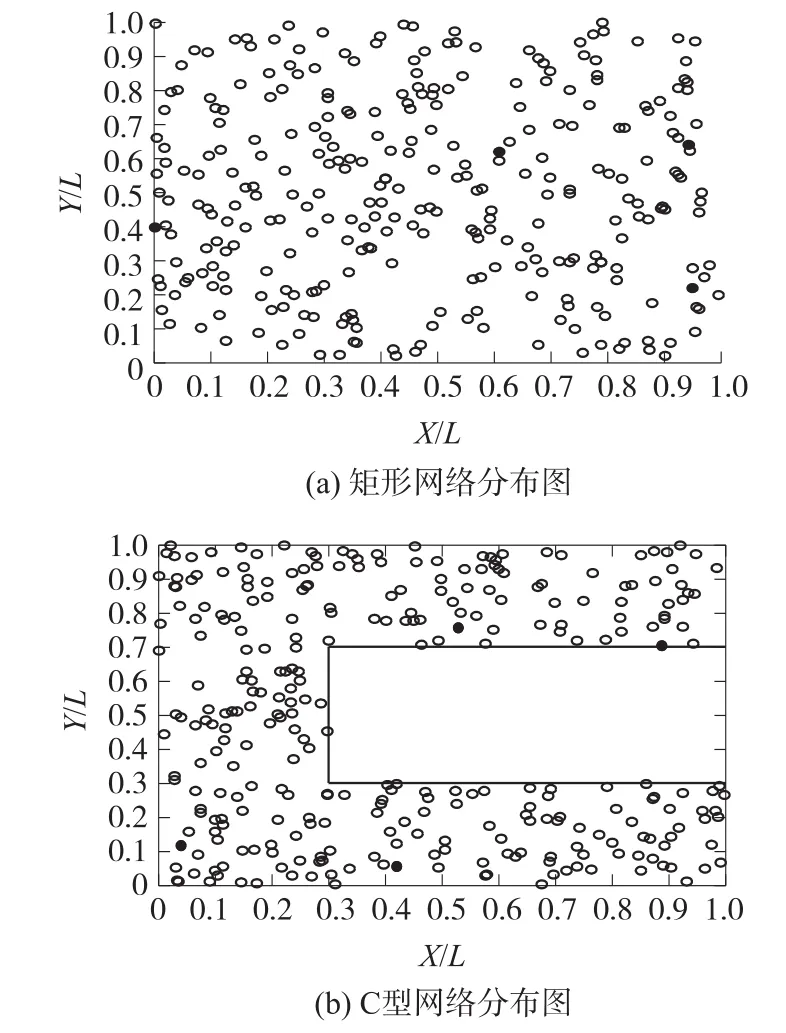
图2　理想传输模型下的网络分布

图3　理想传输模型下矩形网络的定位

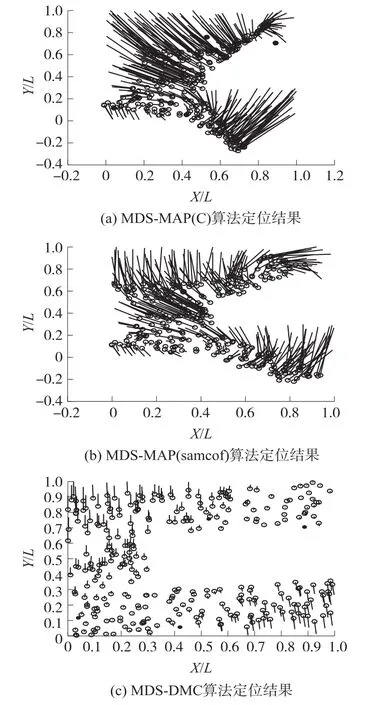
图4　理想传输模型下C形网络的定位

由实验结果可知，在矩形网络中，MDS-MAP （C）算法的平均定位误差为18.7%；MDS-MAP （smacof）算法的平均定位误差有了的改善，为16.9%；而MDS-DMC算法的平均定位误差仅为4.1%，有效的提高了定位的精度。在C型网络中，由于不规则网络的影响，出现了拓扑空洞的情况，最短路径距离矩阵存在较大的误差，导致MDSMAP（C）算法的平均定位误差高达117.8%，而采用MDS-MAP（smacof）算法和MDS-DMC算法的平均定位误差分别为95%和17%，MDS-DMC算法大幅度的减小了平均定位误差。因此，在C型网络中，MDS-DMC算法可以有效减少最短路径距离的差异，改善定位性能，提高对不规则网络的适应性。

3.2非理想传输模型下的定位

非理想传输模型的定位可用不规则的信号模型来模拟实际的环境，采用不规则度DOI（Degree of Irregular）表征锚节点的传播信号在传输的过程中受到的影响，DOI值反映了锚节点信号广播的不规则程度。该实验主要比较三种算法在非理想传输模型的不同网络拓扑下的性能，在实验场景的两种网络拓扑下，随机部署300个节点，在通信半径为0.2L以及DOI为0.2的情况下，矩形网络平均连通度为30.3，C型网络平均连通度为35.9，分别用MDS-MAP（C）算法、MDS-MAP（smacof）算法和MDSDMC算法进行定位。该实验的节点分布以及定位误差如图5~图7所示。

图6　非理想传输模型下矩形网络的定位

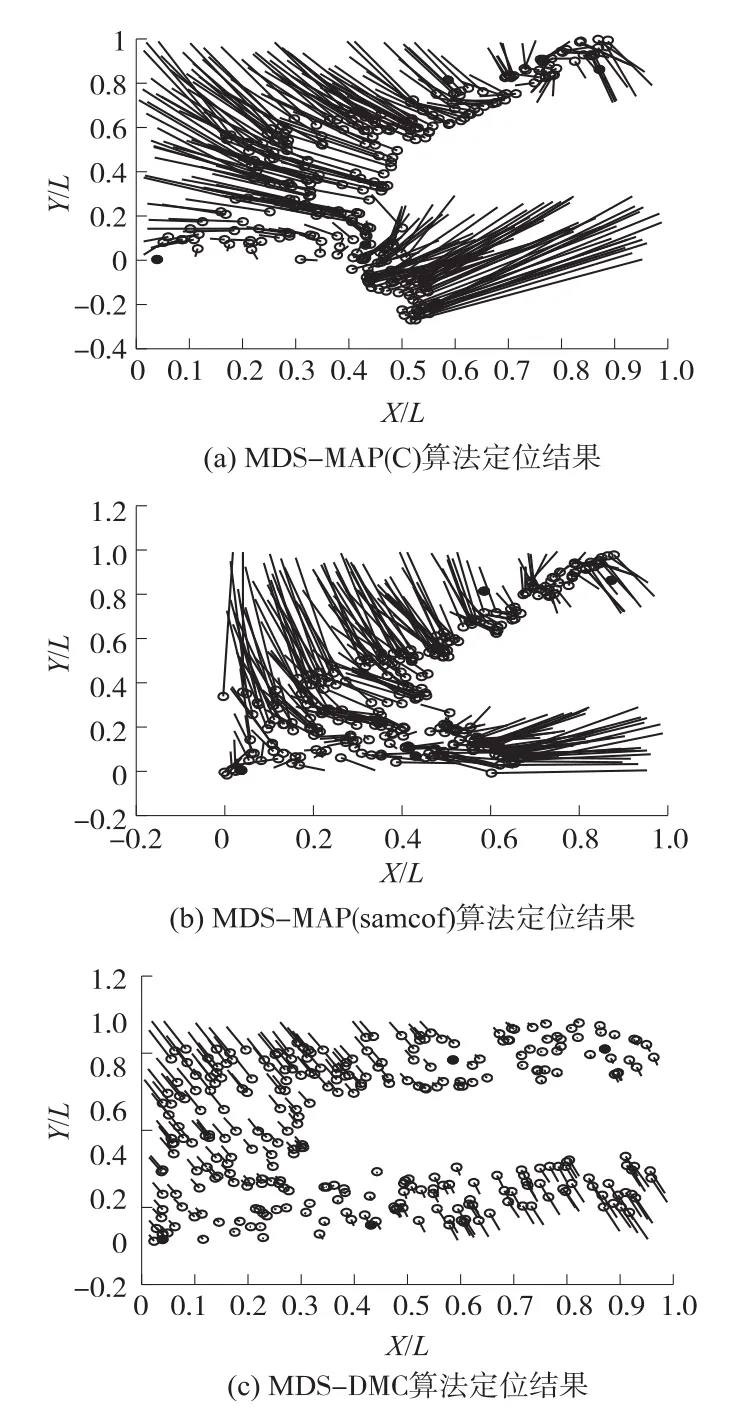
图7　非理想传输模型下C形网络的定位

由实验结果可知，在非理想传输模型的矩形网络中，MDS-MAP（C）算法、MDS-MAP（smacof）算法以及MDS-DMC算法的平均定位误差分别为20.7%、17.4%和8.1%，MDS-DMC算法的定位性能有了明显的改善。而在非理想传输模型的C型网络中，由于最短路径距离矩阵差异的影响不同，MDS-MAP （C）算法、MDS-MAP（smacof）算法以及MDS-DMC算法的平均定位误差分别为118%、107%和18.1%，MDS-DMC算法定位性能的提升更为显著。因此，MDS-DMC算法能够较稳定的适应非理想传输模型的节点定位，提高不规则网络的节点定位精度。

3.3不同连通度的定位误差

该实验主要比较三种算法在不同通信半径和连通度下的性能。在实验场景的两种网络拓扑下，随机部署300个节点，节点通信半径r分别取0.125L、0.15L、0.175L、0.2L、0.225L和0.25L时，矩形网络的连通度分别为13.6、18.7、25.1、31.1、38.0和48.3，C型网络的连通度分别为16.5、22.8、29.1、38.2、45.1和51.3。实验结果如图8所示。

从图8可以看出，MDS-DMC算法在不同连通度的定位性能均优于MDS-MAP（C）算法，在连通度较低的情况下，MDS-DMC算法的定位精度有了明显的提高，特别是在C型网络中，定位精度的提高幅度更大。因此，与MDS-MAP（C）算法相比，MDS-DMC算法在不规则网络拓扑下有更好的适应性，在WSN的定位应用中具有明显的优势。

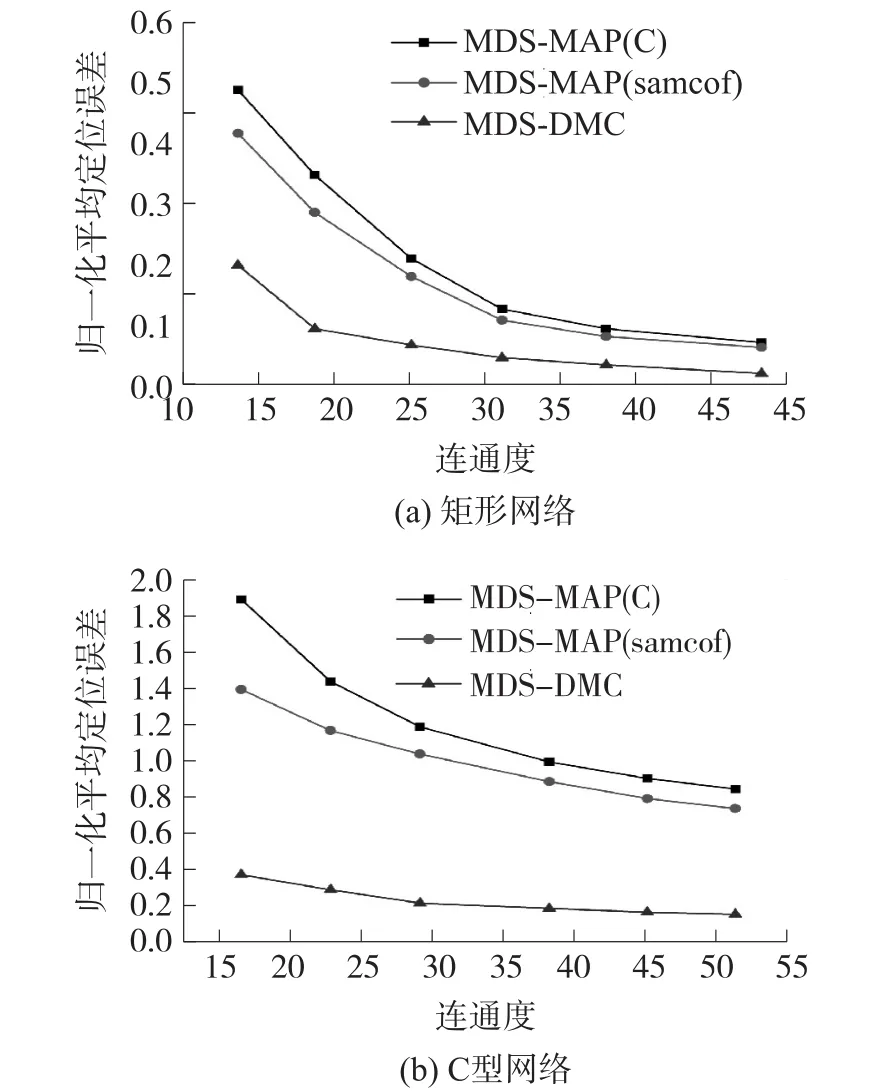
图8　不同连通度的归一化平均定位误差比较

4　结论

①针对MDS-MAP（C）算法中的距离矩阵问题，提出MDS-DMC算法。该算法采用启发式搜索的最短路径距离修正策略来减小最短路径距离与实际欧氏距离之间的误差，有效地提高了节点的定位精度和对不规则网络的适应性；引入smacof算法迭代误差函数取替SVD分解来优化节点定位的求解过程，进一步提升了算法的性能。

②在理想传输模型、非理想传输模型以及不同传输半径和连通度的算法仿真对比实验中，MDSDMC算法均表现出比MDS-MAP（C）算法更加优异的性能，进而验证了改进方法是正确和有效的。

③减小最短路径距离与实际欧氏距离之间的误差是提高多维标度节点定位算法性能的有效途径之一。如何进一步减小距离矩阵之间的差异是后续重点的研究工作。

参考文献：

［1］Liu Qiang，Huang Xiaohong，Leng Supeng，et al. Deployment Strategy of Wireless Sensor Networks for Internet of Things［J］. China Communications，2011，8（8）：111-120.

［2］侯洪涛，周鸿伟，李群，等.卫星导航系统接收传感器网络的攻击检测研究［J］.系统工程与电子技术，2014，36（6）：1195-1200.

［3］王福豹，史龙，任丰原.无线传感器网络中的自身定位系统和算法［J］.软件学报，2005，16（5）：857-868.

［4］张亚明，史浩山，刘燕，等.不对称链路环境下的WSN节点定位算法［J］.传感技术学报，2014，27（3）：320-326.

［5］刘瑜，衣晓，何友.基于分治求精的无线传感器网络节点定位算法［J］.系统工程与电子技术，2012，34（9）：1906-1913.

［6］钱志鸿，王义君.面向物联网的无线传感器网络综述［J］.电子与信息学报，2013，35（1）：215-227.

［7］Park J W，Park D H，Lee C. Angle and Ranging Based Localiza⁃tion Method for ad hoc Network［J］. The Journal of Supercomput⁃ing，2013，64（2）：507-521.

［8］袁鑫，吴晓平，王国英.线性最小二乘法的RSSI定位精确计算方法［J］.传感技术学报，2014，27（10）：1412-1417.

［9］彭宇，王丹.无线传感器网络定位技术综述［J］.电子测量与仪器学报，2011，25（5）：389-399.

［10］Macagnano D，de Abreu G. Algebraic Approach for Robust Local⁃ization with Heterogeneous Information［J］. IEEE Transactions on Wireless Communication，2013，12（10）：5334-5345.

［11］Shang Y，Ruml W，Zhang Y，et al. Localization from Mere Connec⁃tivity［C］//Proceedings of the 4th ACM International Symposium on Mobile Ad Hoc Networking and Computing. New York：ACM Press，2003：201-212.

［12］Shang Y，Ruml W. Improved MDS-based localization［C］// Twen⁃ty-Third Annual Joint Conference of the IEEE Computer and Com⁃munications Societies. Washington：IEEE Press，2004：2640-2651.

［13］Vivekanandan V，Wong V W S. Ordinal MDS-Based Localisation for Wireless Sensor Networks［J］. International Journal of Sensor Networks，2006，1（3）：169-178.

［14］Regalia P A，Wang J. On Distance Reconstruction for Sensor Net⁃Work Localization［C］// Proceedings of 2010 IEEE International Conference on Acoustics Speech and Signal Processing，Washing⁃ ton：IEEE Press，2010：2866-2869.

［15］黄亮，王福豹，段渭军，等.基于距离重构的无线传感器网络多维定标定位算法［J］.传感技术学报，2013，26（9）：1284-1287.

［16］温龙飞，崔灵果，张百海，等.不均匀布置传感器网络定位优化算法［J］.兵工学报，2013，34（05）：639-643.

［17］张亚杰，段渭军，王福豹，等.改进的距离重构三维定位算法［J］.传感技术学报，2014，27（12）：1681-1686.

任克强（1959-），男，教授，硕士研究生导师，主要研究方向为嵌入式系统、无线传感器网络等，jxrenkeqiang@163.com；

庄放望（1988-），男，硕士研究生，主要研究方向为无线传感器网络。

A Preliminary Study of Zanthoxylurn Bungeanum Maxim Varieties Discriminating by Computer Vision*

WU Lili*，XING Yuqing，ZHENG Baozhou，LIN Aiying
（College of Sciences，Henan Agricultural University，Zhengzhou 450002，China）

Abstract：Zanthoxylurn Bungeanum Maxim is a kind of important ingredients for cooking and traditional Chinese medicine. In this paper，the computer vision technology was introduced to discriminate the varieties of Zanthoxylurn Bungeanum Maxim rapdily. The Zanthoxylurn Bungeanum Maxim image of six categories were obtained by the com⁃puter vision hardware device，and the total number of images was 90，of which 60 were used as training samples and 30 as test samples. The 10 feature parameters of color and texture features were extracted from all the samples，which were identified by the probabilistic neural network. The correct recognition rate was 93.33%. The discrimination method of Zanthoxylurn Bungeanum Maxim varieties by computer vision can quickly and accurately extract the char⁃acteristic data of the Zanthoxylurn Bungeanum Maxim samples，which lays the technical foundation for batch sorting. Key words：computer vision；color feature；texture feature；probabilistic neural network；Zanthoxylurn Bungeanum Maxim

doi：EEACC：6135;7230G10.3969/j.issn.1004-1699.2016.01.023

收稿日期：2015-08-06修改日期：2015-10-20

中图分类号：TP393

文献标识码：A

文章编号：1004-1699（2016）01-0129-07