小学数学结构化教学的实践与思考

【摘要】通过整合知识板块、帮助思维结构化、倡导教学结构化来探讨小学数学结构化教学，并从实践中明确树立系统教学理念，将不同领域的知识及其育人价值通过整体架构、有机渗透，融合于教学过程中，有助于发展学生的数学核心素养。

【关键词】结构化教学；整合；思维；核心素养

【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009（2016）06-0035-03

【作者简介】徐微，江苏省镇江市中山路小学（江苏镇江，212000），一级教师，镇江市京口区数学学科带头人，江苏省小学数学课程教材改革实验先进个人。

如今，在学校日常教学中依然存在着这样两个问题：一是教师缺乏对数学知识的整体结构认识，过分依赖教材的单元和课时划分，局限于单课时教学，割裂了知识结构，削弱甚至偏离了数学学科的课程目标；二是教师缺乏对学生学习过程的整体设计，满足于当前情境或活动的设计，策划的视野短期化，忽略甚至局限了学生的数学思维和学习能力的长期培养。作为教师应该树立系统教学理念，将不同领域的知识及其育人价值通过整体架构、有机渗透，融合于教学过程中，使学生的学科素养得到整体提升。基于此，笔者进行了如下的实践与思考。

一、小学数学结构化教学的实践策略

1.整合知识板块。

结构的关联能使知识的教学和能力的发展呈现一条清晰的脉络，但这样的结构设计不是唯一，不应成为教学的桎梏，同样这样的结构也不应该固化，使教学陷入枯燥的模式化。在教学中，教师可以依据单元知识之间的并联关系、递进关系灵活设计教学流程。

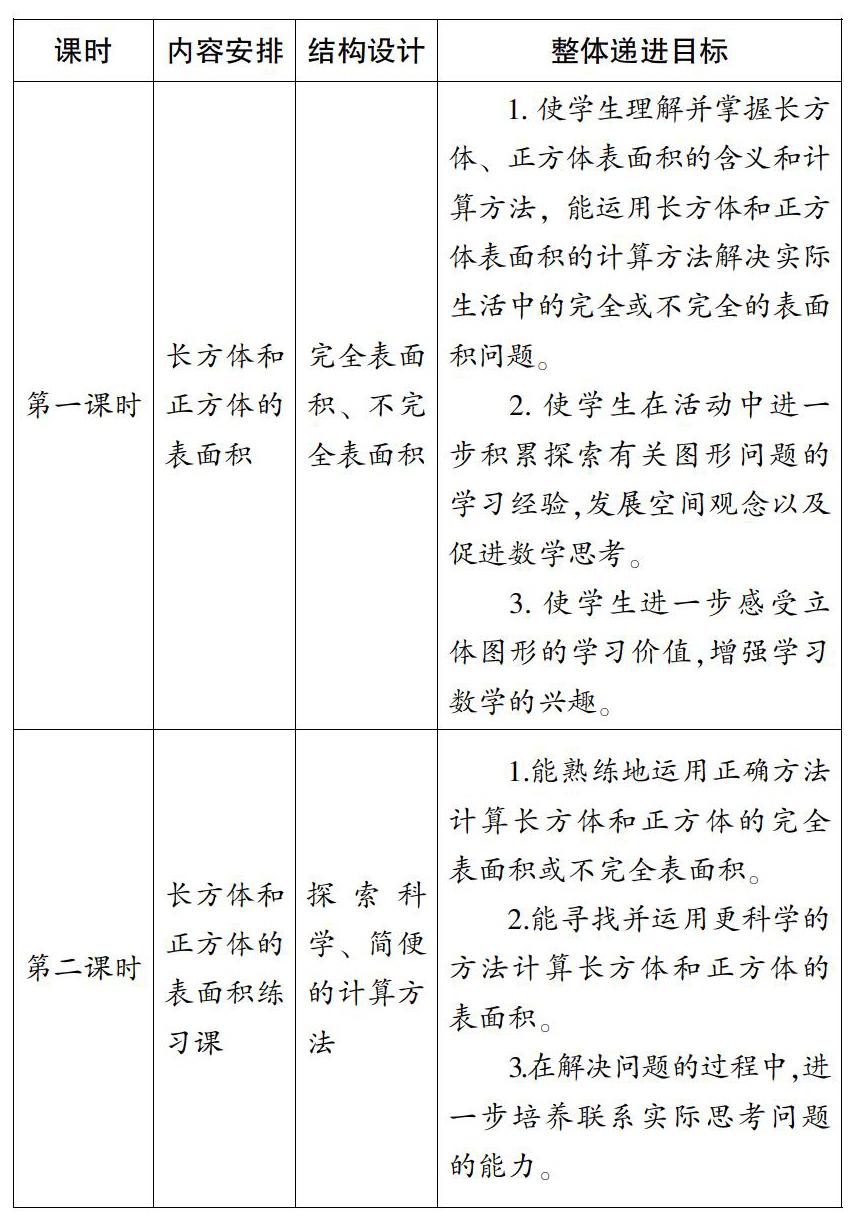
（1）整合课时知识。受40分钟教学时间的限制，有些内容被划分成两个或三个独立课时，比如：在苏教版六上《长方体和正方体》单元的教学中，“长方体和正方体完全表面积计算”和“长方体和正方体不完全表面积计算”这两个课时的学习都是建立在对这两种立体图形的认识和研究了它们的展开图的基础上进行的，两课的内容联系紧密，探究方法、教学过程基本一致。于是，笔者尝试对这两课进行如下调整：

通过实际教学，证明尝试是成功的，学生不仅能很好地达成学习目标，还能对长方体和正方体表面积计算的探究过程形成清晰认识，对实际遇到的各类完全表面积或不完全表面积均能正确灵活的计算。这样深入知识内部去整体把握、科学设计，摆脱了原有课时的桎梏，充分尊重学生的学习需求，灵活使用教材，从而达到让教材为教学服务、为学生发展服务的目的。

（2）整合单元知识。在实际教学中，我们发现有些年段单元知识前后的联系非常密切，不仅有利于教师在教学中保持知识的整体性，还有利于学生感受知识的整体性。例如苏教版五上第三、四、五单元，先后进行《小数的意义和性质》《小数加法和减法》《小数乘法和除法》的教学，对小数的学习通过认识和运算去整体把握，块面完整。而苏教版教材中分数知识的块面划分就有了区别，三、五、六年级均涉及，其中六上第二、三单元学习《分数乘法》和《分数除法》后，第四单元研究《解决问题的策略》，然后第五单元再学习《分数四则混合运算》。从教师角度看，不利于教学的整体结构；从学生的角度看，不利于学生头脑中对知识的整体建构。基于此，笔者在实际教学中将《分数乘法》《分数除法》《分数四则混合运算》三单元整体教学，脉络清晰，一气呵成。

2.帮助思维结构化。

结构化教学是一项长期的工程，其价值不仅限于知识的形成，更多地体现在学生对知识结构的把握和把握结构后自主建构学习的积极状态。

（1）整体感悟。思维整体的结构化在复习课中体现最明显，复习不是对单元知识的简单重复，而是依据复习内容采用新的复习策略，以此帮助学生保持较高的复习兴趣。如复习苏教版六上《分数乘法》单元时，笔者要求学生课前自我复习，并根据自己的理解制作知识结构图以展示整个单元的知识体系，课上分组交流汇报。通过这样的形式，学生能够整体地把握内容之间的关系，并能积极地进行讨论，继而在整体感悟的基础上，主动建构和完善自己的认知结构和思维方式。

（2）学会迁移。在由教到学逐步放手的过程中，迁移知识形成的过程性结构尤为重要，教师带领学生在一定程度上还原前人发现和发展某一领域知识的过程，并将这一过程结构化，帮助学生了解和掌握这个发现探索的过程性结构，然后自觉迁移到教材以外的探索中。如从探索加法、乘法运算律引导学生去验证减法和除法中是否存在类似的运算律，从探索平行四边形面积拓展到三角形的面积计算。教师只有学会利用迁移，才能激发起学生更多的运用和创造热情。

（3）培养能力。基于结构的教学，要让学生意识到结构的存在，并自觉地运用结构展开学习。因此，每一单元、每一学期或每一学段学习结束后，指导学生进行复习与整理，会让学生体会到知识的系统化和条理化。从系统梳理到整体结构化地把握知识，从寻找知识间的差异到沟通知识间的内在联系，从个性化整理到创造性呈现，学生对整个过程的经历与体验有利于学生形成综合的学习能力，发展数学核心素养。

3.倡导教学结构化。

教师要在深入解读课程标准、正确把握教材、明晰学生学习起点的基础上，科学制定目标。在纵向上，依据学生年段特点，从学习心态、知识积累、能力、习惯等方面进行分析；在横向上，紧扣知识间联系，预设学生发展的可能，以及学生面对具体的数学知识时的心理状态，分析学生现有知识经验对新知学习的影响。同时，科学评估学生的潜能，积极创设有利于学生学习和探索的思维空间和心理空间。关注不同基础学生在新知学习过程中的不同表达方式，关注差异性。例如：感悟统计思想方法贯穿整个小学阶段，从把相同的放在一起数到画勾、画正字、单式统计表、复式统计表、条形统计图、折线统计图、扇形统计图。再比如：学习比较的思想，从最初比较两类事物的个数，到数形结合给出条件比较，成了实际问题的雏形；从直观实物的比较，到抽象出线段图，这一过程把数学思想方法的长期感悟、持久熏陶，特别是结构的整体性表现得淋漓尽致。

二、小学数学结构化教学的价值认识

从列维的结构主义到皮亚杰的认知结构理论、布鲁纳的“学科基本结构”思想，以及奥苏伯尔提出“新知识的学习必须以已有的认知结构为基础”这些观点，无一不与“结构”相关。整体结构教学就是要通过回顾、提炼和反思逐步将知识结构内化为学生学习的方法结构，成为新的学习工具。它包括三个层面的结构：

一是展开结构，在前后关联的知识之间有着相似的呈现方式。如在整数中按照“数的意义”、“数的运算”以及“运算的规律”展开，同样方式在小数、分数教学中也遵循，这就是知识展开方式的相似性。同样，在“认数”教学中，不同年级数概念教学都有着相同的展开逻辑：数的意义→数的组成→数位→读写→数的大小比较。随着对数认识的逐步拓展，这些“知识结构”将会潜移默化地被学生个体“吸收”而内化为“认知结构”，帮助学生在整体上对数学知识和方法进行把握，改变碎片化处理数学知识和方法的现象，增强学生学习数学的整体意识，提高学习效率。

二是过程结构，同一类知识有着类似的教学过程。例如教学“运算律”时，一般都按“猜想→验证→概括→拓展”进行；“量的计量”教学按照“材料感知→操作感悟→形成概念→运用巩固”这一过程推进，这些就是相关知识教学的过程结构。认识到这种过程性结构的存在，教师就可以从起始内容开始，努力引导学生了解和把握，使得在后续的学习中，学生能主动迁移，开展学习研究活动。结构化地展开教学过程，学生获得了独立学习的有效路径，便能投入积极主动的学习过程，成为知识、能力和方法的主动建构者和创造者。

三是方法结构，学生在获取数学知识的过程中经常采用相同的学习方法。如：学习整数加减乘除的运算时，通常都采用“讲算理→明算法→多应用”的方式；学习正方体、长方体、圆柱体的表面积计算时，通常采用“想特征→试操作（剪开成平面图形）→说联系→多应用”的方法。当学生明晰了这样的结构，自主学习才有了可能，在遇到相似的问题时不再依赖教师，而是自己进行方法结构的正迁移。在这样的结构教学中，教师关注学生的不仅仅是获取知识量的多少、解题熟练程度和是否掌握了解题技巧，而是关注学生是否获得了思维方式与行为方式的双支撑。这种支撑能促进学生把已掌握的知识自觉地提炼成简洁的原理性结构，从而使学生拥有探究新知识和新事物的能力，如此，将极大激发学生学习数学知识的自主性，并为终身学习打下良好的思维基础。

如果教师能够合理把握好数学知识的整体框架，并能结构化地设计教学过程，教学就不会沦为“粗暴的给予数学知识碎片”。当我们站在学生的角度帮助学生在学习的过程中边学边“串”，将数学学习整体化，最终学生得到的不仅是数学“知识链”，更多的是数学思维能力、学习能力的提升。当结构化教学的渗透成为一种自觉时，必然能改变教师的思维方式，激发学生的强大学习动力，进而发展学生的数学核心素养，让学生的思维走向自主建构的结构化，为学生的终身发展奠定坚实的基础。