改进粒子群算法在主动磁悬浮轴承系统中的应用*

张建生 王一夫 马啸宇 沈莹雅

(①南通大学电气工程学院，江苏 南通 226019；②常州工学院电气与光电工程学院，江苏 常州 213002)

改进粒子群算法在主动磁悬浮轴承系统中的应用*

张建生①王一夫①马啸宇①沈莹雅①

(①南通大学电气工程学院，江苏 南通 226019；②常州工学院电气与光电工程学院，江苏 常州 213002)

通过分析得知，主动磁悬浮轴承系统本身是一个不稳定系统，可以采用PID控制器对其进行控制。但是传统PID控制在主动磁悬浮轴承系统中还存在着不足之处，为此可以将粒子群优化算法与常规PID控制相结合，对PID控制器中的参数进行优化，使系统能够达到更好的控制效果。采用了一种改进粒子群算法，对算法中的惯性权重w进行自适应调节，从而使得算法能够更快、更准确地寻找到最优值。通过Matlab/Simulink构建系统模型并进行仿真对比，改进粒子群算法可以使得系统达到更好的控制效果。

主动磁悬浮轴承；改进粒子群算法；PID控制；MATLAB

为了解决传统机械中的转子动力学问题，可以通过对转子进行无接触、无润滑、无磨损的悬浮支撑，并且进行动力学行为中的主动控制，这种技术方案就是主动磁悬浮轴承，简称为磁轴承[1]。和传统的轴承相比，磁悬浮轴承还有许多优点，比如：无摩擦、维护费用低、低噪音、精度高和运行过程可调控。另一方面，主动磁悬浮轴承可以比被动磁悬浮轴承调整更多的参数，比如：阻尼系数、静态刚度和动态刚度、悬浮位置等。对磁轴承系统分析可知，系统是开环不稳定的，因此需要进行闭环控制。但是普通的闭环控制仍然不能使系统趋于稳定，所以我们需要另外加上一个PID控制器。在PID控制器中，最重要的3个参数是KP、KI和KD，如何对这3个参数进行准确的设置一直是专家学者所要解决的问题[2]。粒子群优化算法就可以很好地解决这个参数设置问题，该优化算法能够快速并且准确地找到全局最优解，并且已被证明在多种优化环境中都可以进行应用。和传统的优化算法相比，它的全局搜索能力更强、计算速度更快，因此更具有优势。但是与此同时，传统的粒子群算法仍然有一些不足之处，本文就是基于改进的粒子群算法，来对磁悬浮轴承系统进行PID控制。

1 主动磁悬浮轴承控制系统模型

单自由度主动磁悬浮轴承控制系统模型图如图1所示。

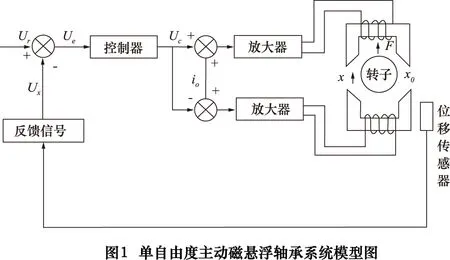
从图1中可以看出，控制器、功率放大器、电磁铁、转子和位移传感器这五个部分构成了主动磁悬浮轴承系统，这里采用的双电磁铁差动激磁连接方式。图1中，i0为转子平衡位置处的电流，x0为转子的平衡位置；当转子向上偏移一定的距离x远离了原来的平衡位置时，就会被位移传感器检测到此时的位移偏差信号，然后位移信号经过处理转换成相应的电压信号Ux，Ux与转子平衡时的电压Ur进行比较就能够得到偏差信号Ue，紧接着通过计算得出控制信号Uc，再通过功率放大器的信号处理得到控制电流i，最终使得转子向下运动并最终回到原来的平衡位置。

假设忽略转子和铁芯中的磁阻、磁滞和涡流及绕组漏磁，根据电磁学理论，电流i产生的电磁力为：

(1)

式中：μ0=4π×10-7H/m为真空磁导率，S0为气隙面积，N为线圈匝数；i为线圈电流；x为转子与电磁铁之间的距离。

图1中，转子在重力方向上受到上下电磁铁产生的电磁合力为：

(2)

式中：F为总的电磁力，i0为电磁线圈的偏置电流即转子平衡位置处的电流；i为控制电流；x0为转子平衡位置处的位移；x为偏移位移。根据牛顿定律md2x/dt2=mg-F，并代入式(2)得到主动磁悬浮轴承单自由度运动方程为：

(3)

由式(3)知，主动磁悬浮轴承数学模型为一个二次非线性微分方程，电磁吸力与激磁电流、气隙间距均为非线性关系。常用的方法是通过一些线性控制策略来获得很好的控制效果，因此，磁场力F中的力/位移与力/电流的关系需要在工作点(x0、i0、mg)处做线性化处理。这个工作点表示了一个期望的理想平衡位置，即Fm(x0,i0)=mg，图2描述了这些关系曲线[1]。

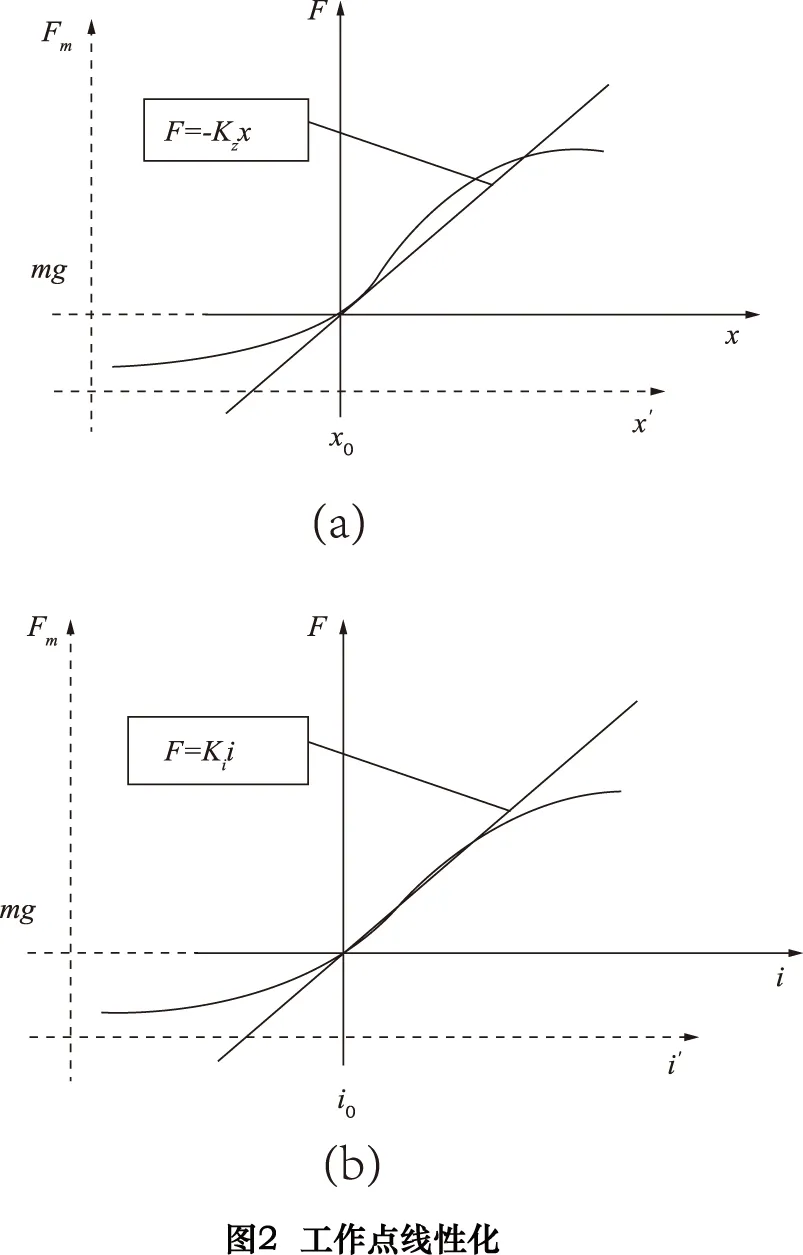
将式(1)在平衡点x=x0，i=i0处作泰勒级数展开：

(4)

将式(4)舍去二次及以上高次项后并计算代入偏导数，得到电磁力F(x,i)的表达式为：

(5)

式中：Ks=-μ0S0N2i02/2x03为位移刚度系数；Ki=μ0S0N2i0/2x02为电流刚度系数。由于在平衡点(x=x0，i=i0)处，Fm(x0,i0)=mg，将式(5)代入式(3)中，得到线性化后的磁悬浮轴承系统开环数学模型为：

(6)

将式(6)进行拉氏变换并化简后，得到磁悬浮轴承系统的开环传递函数为：

(7)

2 改进的粒子群优化算法

2.1 粒子群算法简介

在专家学者对鸟群的行为进行研究的过程当中，诞生了粒子群算法[5]。他们发现，现实生活中的许多优化问题都可以使用这种粒子群算法。在粒子群算法中，每一个优化问题的潜在解都可以看成是一个粒子；并且每个粒子都有一个属于自己的适应值，这个适应值是由所需要解决问题的目标函数决定的，此外每个粒子的运动距离和方向都由一个速度来控制。最终，种群里每个粒子就以此时的最优粒子为目标方向进行搜索。

每个粒子根据下面的公式来更新自己的位置和速度：

vid=w×vid+c1r1(pid-xid)+c2r2(pgd-xid)

(8)

xid=xid+vid

(9)

式中：c1，c2是学习因子；r1，r2是[0，1]范围内的均匀随机数。

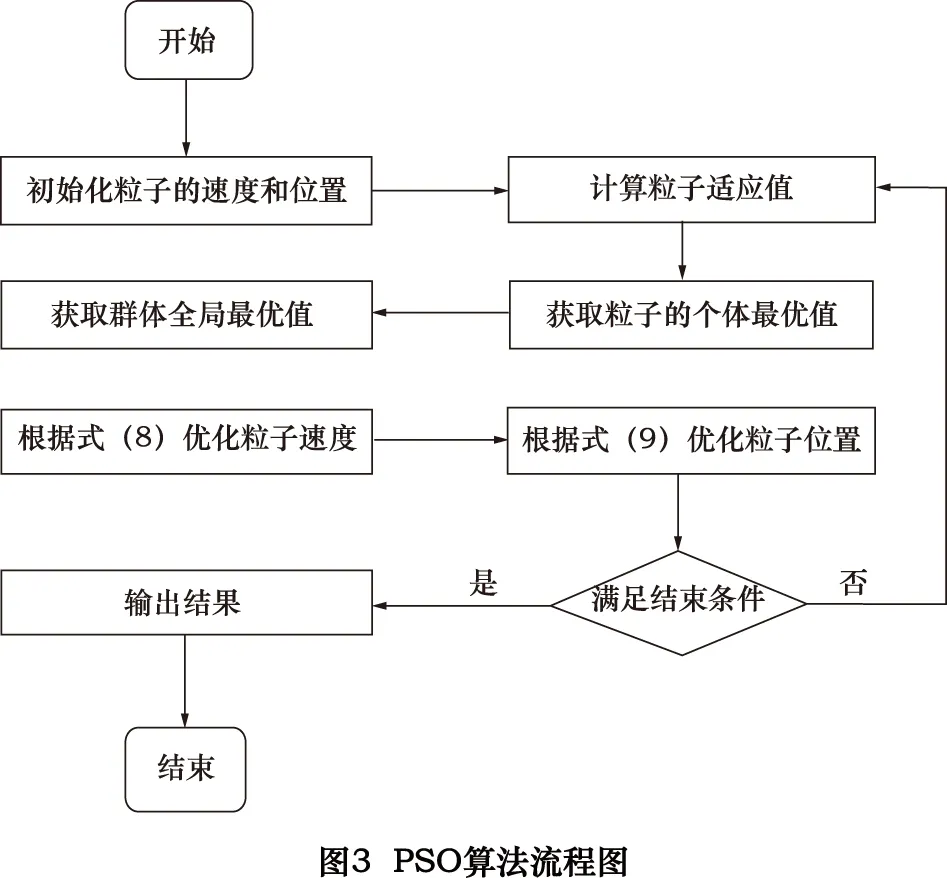
基本粒子群算法的流程图如图3所示[9]。

2.2 改进的粒子群算法

惯性权重w在粒子群算法中十分重要。增大w值可以提高算法的全局搜索能力，减小w值则可以提高局部搜索能力。因此，要想避免算法陷入局部最优同时又能够提高搜索效率，就必须想办法得到最为合适的惯性权重w。

粒子当前位置在全局当中是否合适可以用其适应度来反映。一些适应度较高的粒子pi所在的区域可能存在着能够更新全局最优点的px。所以，想要及时更新px并迅速找到全局最优解，就应该减小粒子pi的惯性权重w，提高粒子局部寻优能力；同时，对于那些当前位置较差的粒子而言，就必须要跳出当前所在区域，此时应当增大惯性权重w，提高粒子全局搜索能力从而可以更快地找到全局最优点。

粒子距全局最优点的距离也会影响惯性权重w的大小，不同粒子的惯性权重会随着迭代次数和距全局最优点距离的增加而递减，即惯性权重w的值会根据粒子的不同位置而发生动态变化。在这里我们可以采用一种自适应权重法，其非线性动态惯性权重系数公式为：

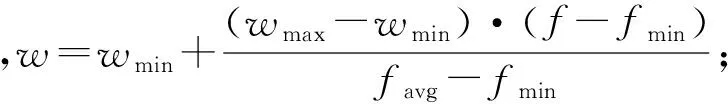
当f>favg时，w=wmax。

式中：f为实时的粒子目标函数值，favg和fmin分别为当前所有粒子的平均值和最小目标值。

从上面的公式可以看出，粒子的惯性权重值随着目标函数值的改变而改变。当粒子的目标值分散时，减小惯性权重值；当粒子的目标值一致时，增加惯性权重值。

算法的基本步骤如下：

(1)随机初始化种群中各个粒子的位置和速度。

(2)计算每个粒子的适应度值，将此时的位置和适应值存放在粒子的个体极值pbest中，再通过相互比较将所有个体极值中最优适应值的位置和适应值保存在全局极值gbest中。

(3)更新粒子的位置和速度：

xi,j(t+1)=xi,j(t)+vi,j(t+1)，j=1,2,…,d

(4)更新权重：

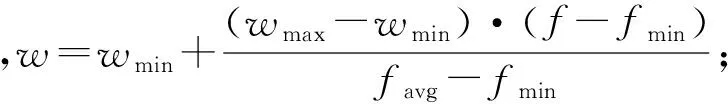
当f>favg时，w=wmax。

(5)将每个粒子的适应值和粒子中的最好适应值相比较，如果适应值较为接近，则全局粒子最好的位置就是此时的位置。比较当前所有的pbest和gbest，更新gbest。

(6)当算法达到其停止条件时，则停止搜索并输出结果，否则返回到第(3)步继续搜索。

2.3 函数测试

本文将采用三个标准测试函数来对标准PSO算法及其改进算法进行实验研究，这些标准函数都是专家经过精心设计和严格测试的，如果有优化算法能够准确并且迅速地解决某一个标准测试的优化问题，那么在大部分优化问题中就可以使用这个优化算法[5]。

(1)Rosenbrock函数：

(10)

在这里涉及到的参数有：学习因子c1=2，学习因子c2=2，最大迭代次数M=100，搜索空间维数D=30，初始化种群个体数目N=50，标准粒子群算法(PSO)的惯性权重w=0.7，改进粒子群算法(I-PSO)的惯性权重wmax=0.8，wmin=0.6。

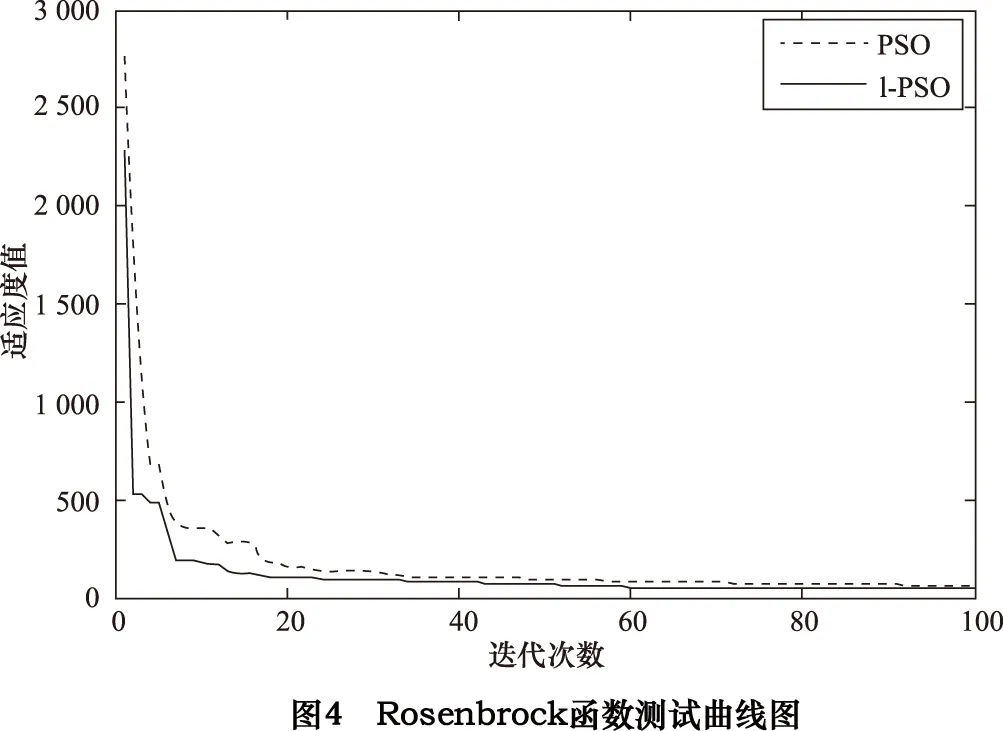
函数测试曲线如图4所示。

(2)Griewank函数：

(11)

在这里涉及到的参数有：学习因子c1=2，学习因子c2=2，最大迭代次数M=100，搜索空间维数D=30，初始化种群个体数目N=50，标准粒子群算法(PSO)的惯性权重w=0.7，改进粒子群算法(I-PSO)的惯性权重wmax=0.8，wmin=0.6。

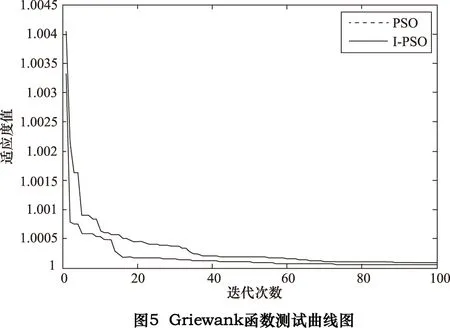
函数测试曲线如图5所示。

(3)Rastrigin函数：

(12)

在这里涉及到的参数有：学习因子c1=2，学习因子c2=2，最大迭代次数M=400，搜索空间维数D=30，初始化种群个体数目N=50，标准粒子群算法(PSO)的惯性权重w=0.7，改进粒子群算法(I-PSO)的惯性权重wmax=0.8，wmin=0.6。

函数测试曲线如图6所示。

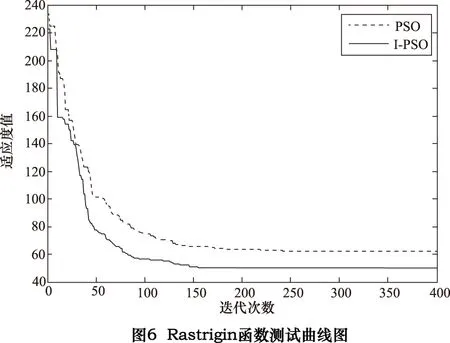
从三个函数测试曲线图中可以清楚地看出，改进的粒子群算法能够比标准粒子群算法更快、更准确地找出目标函数的最小值。因此，我们认为改进的粒子群优化算法可以很好的应用在主动磁悬浮轴承系统的优化问题中。

3 系统仿真分析

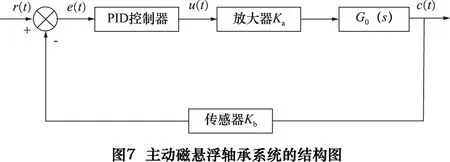
主动磁悬浮轴承系统的结构图如图7所示[6]。

图中所表示的是带有PID控制器的闭环控制回路，其中PID控制器可以表示为[10]：

(13)

系统的输入可以给为单位阶跃响应，经相应的传递函数计算和拉普拉斯变换，可以得出e(t)、u(t)和c(t)，还可以计算出上升时间tu。

在磁轴承系统中，目标函数采用基于时域指标的设计方法，这个方法是将多个性能指标的加权之和的最小值作为优化目标，使得系统能够有较好的响应。在这里，可以取目标函数为：

(14)

为了减小超调量对系统的影响，也把超调量算作目标函数的一项，并辅以一定的系数，则目标函数为：

(15)

式中的w1、w2、w3和w4为权值，并且w4≫w1，在这里我们可以取w1=0.8，w2=0.001，w3=20，w4=100；ey(t)=y(t)-y(t-1)，y(t)为被控对象输出[8]。

有了目标函数以后，就可以运用改进的粒子群优化算法对系统参数进行优化，再在MATLAB/simulink中构建系统的结构图进行仿真研究[7]。系统的响应曲线如图8所示。在主动磁悬浮轴承系统中，涉及的参数为：m=12kg，Ka=3.6，Kb=5 000N/m，Ks=-2.102 8×106N/m，Ki=420.56N/A。

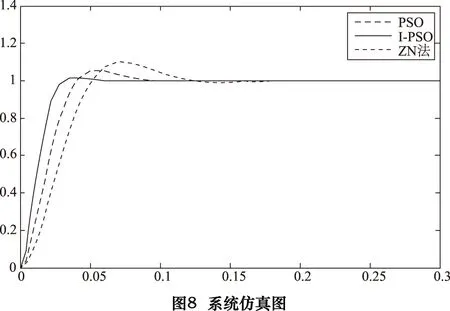
图8中相关参数如表1所示[4]。图8中折线表示的是标准粒子群算法(PSO)得出的曲线，实线表示的是改进粒子群算法(I-PSO)得出的曲线，虚线表示的是传统ZN法得出的曲线。从图8和表1中可以清楚地看出，与传统ZN法相比两种粒子群算法都使得系统的稳定性和动态性能得到了提升；进一步比较可以看出改进粒子群算法可以使得系统获得更好的稳定性和动态性能，从而说明了改进粒子群算法可以在主动磁悬浮轴承系统中得到很好的应用。

表1 仿真图参数表

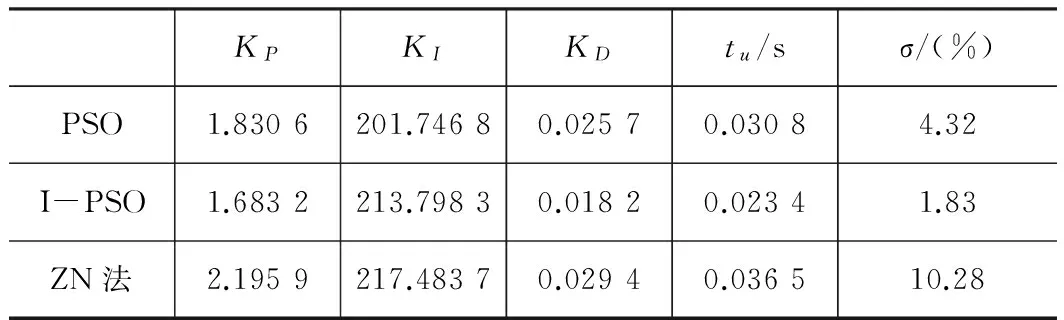
KPKIKDtu/sσ/(%)PSO1.8306201.74680.02570.03084.32I-PSO1.6832213.79830.01820.02341.83ZN法2.1959217.48370.02940.036510.28

4 结语

针对主动磁悬浮轴承系统的高度非线性和本质不稳定等问题，本文采用了改进粒子群算法与传统PID控制相结合的方式，使得传统PID控制可以更好地发挥控制效果，从而提升了整个系统的运行性能。因此，在主动磁悬浮轴承系统的PID控制过程中，我们可以采用改进的粒子群优化算法，并且也可以将它应用在其他类似的工作场合中。

[1]GerhardSchweitzer,EricH.Maslen.磁悬浮轴承：理论、设计及旋转机械应用[M].北京：机械工业出版社，2012.

[2]Kuan-YuChen,Pi-ChengTung,Mong-TaoTsai,etal.Aself-tuningfuzzyPID-typecontrollerdesignforunbalancecompensationinanactivemagneticbearing[J].ExpertSyst.Appl, 2009,Vol.36.

[3]Hung-ChengChen.OptimalfuzzyPIDcontrollerdesignforanactivemagneticbearingsystembasedonadaptivegeneticalgorithms[J].MathematicalStructuresinComputerScience, 2014, 24 (5).

[4]胡寿松.自动控制原理简明教程[M].北京：科学出版社，2008.

[5]李丽，牛奔.粒子群优化算法[M].北京：冶金工业出版社，2009.

[6]唐贤伦，张衡.基于多Agent混沌粒子群优化的磁悬浮系统PID控制器[J].信息与控制，2013,42(6):758-764.

[7]王晓玲，张广明.变论域模糊PID磁悬浮轴承控制系统仿真[J].仪表技术与传感器，2012(12):144-147.

[8]施文娟.基于ARM微处理器开发平台的对磁悬浮轴承的控制研究[D].苏州：苏州大学，2006:76-79.

[9]温正.精通MATLAB智能算法[M].北京：清华大学出版社，2015.

[10]陶永华，尹怡欣.新型PID控制及其应用[M].北京：机械工业出版社，1998.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Improved particle swarm optimization in active magnetic bearing system

ZHANG Jiansheng①②, WANG Yifu①, MA Xiaoyu①, SHEN Yingya①

(①School of Electrical Engineering, Nantong University, Nantong 226019, CHN; ②School of Electrical and Optical Engineering, Changzhou Institute of Technology, Changzhou 213002, CHN)

The analysis shows that the active magnetic bearing system is an unstable system, we can use a PID controller to control it. However, the traditional PID control still has some shortcomings in active magnetic bearing system, we can optimize the PID controller parameters through combining particle swarm optimization algorithm with conventional PID control, and make the system achieve better control effect. This article uses an improved particle swarm algorithm and adjusts its inertia weight w adaptive, so that the algorithm can find the optimal value more quickly and accurately. Through constructing system model by Matlab/Simulink and simulation comparison, improved particle swarm algorithm enables the system to achieve better control effect.

active magnetic bearing; improved particle swarm optimization; PID control; MATLAB

*国家自然科学基金项目(51175052)

TP273

A

10.19287/j.cnki.1005-2402.2016.09.008

张建生，男，1958年生，教授，博士生导师，研究方向为计算机数字控制与控制工程。

(编辑 孙德茂)

2016-01-26)

160913