中位数排序集抽样下总体均值的比率估计方法
2016-03-20王燕
王 燕
(信阳职业技术学院 数学与计算机科学学院, 河南 信阳 464000)
在数据获取和分析的过程中,抽样调查发挥着重要的作用。目前,在现有的排序集抽样方法基础上不断出现新型的抽样方法,例如中位数排序集抽样方法(MRSS)以及极值排序集抽样方法(ERSS)等。[1]在本文中主要通过对两种抽样方法的估计量进行效率对比和实例的证明,从而证明中位数排序集抽样方法对总体均值的比率具有更高的效率和准确度。
一、排序集抽样的优点与发展历程
(一)排序集抽样的优点
在统计数据和分析数据的过程中,抽样调查是重要的收集数据方法,在多个领域的统计调查以及市场数据的分析中都获得较为广泛的应用,发挥着重要的数据统计处理的作用。在统计数据收集的环节中,通过普查所得的数据具有极高的全面性,也具有精准度,但是考虑到实际数据统计的成本与时间并非无限度,因此难以在所有项目中都采取普查的方法收集数据,缺乏实际可行性。例如,在调查池塘中所含有的微生物数量、调查某个省中小学生的平均体重和平均身高等,如此的调查实验如果采用全面普查的方法进行收集数据,将会需要投入大量的成本和时间,因此只能够通过抽样调查的方法来收集数据。与全面普查对比,抽样调查具有着明显的相对优势:一方面,大大地减少全面普查所带来的巨大的费用,节省调查的时间,加快了收集数据的速度;另一方面,选择符合实际需求的抽样方法,有利于提高收集数据的有效性。
通常情况下,基本的抽样方法包括随机抽样方法、分层抽样方法以及系统抽样方法等。为了满足生活与生产中实际问题统计数据的需求,统计学不断发展,并且新的统计方法不断诞生。排序集抽样方法(RSS)是一种覆盖基本抽样方法优点的新型抽样方法,数量相同的测量样本对象含有多方面的总体信息,有利于提高测量样本的典型性和针对性,从而提高数据统计和估计的精确度。尤其对存在明显排序特点但是收集统计数据较为困难的抽样总体,采用排序集抽样方法进行数据收集,优势更为明显。与此同时,还可以通过成本高的调查统计数据的排序进行数据分析。例如,对某公司新研发的商品在全国市场的销售前景进行估计,必须保持产量处于适合的水平,才可以获取最大的利益。在全国范围内对产品需求量进行调查缺乏实际可行性,因此采取抽样的方法进行数据收集。产品需求量和人们的收入水平具有相关性,采用RSS的抽样方法进行抽样。首先把全国省市划分为不同的区域,随机抽取5个样本容量,即为5个排序样本。如下所示:


采用Xi(j,5)表示人均收入样本,其中i代表第i组,j代表第j个样本,Xi(j,5)代表第i组第j个样本。抽取 X1(1,5)、X2(2,5)、X3(3,5)、X4(4,5)、X5(5,5)作为测量样本城市,对这几个样本城的商品需求量进行调查,从中对全国商品需求量进行估算,最后根据估算量确定商品的生产量。
(二)排序集抽样的发展历程
排序集抽样方法于1952年被提出,在1968年,相关学者对该种方法的数学性质进行了分析。后来经过多位学者的改进,基本排序集抽样方法诞生出多种新型的排序集抽样方法。在1996年,极值排序集抽样方法(ERSS)被提出,该方法适用于样本数量为偶数的情况下,对每组样本抽取最大值或者最小值,减少误差,提高可操作性。[2]在1997年,中位数排序集抽样方法(MRSS)被提出,收集数据的效率比极值抽样方法收集数据的效率更加高,并且具有更小的方差。由于在样本总体的统计分析过程中,均值具有着重要的统计意义,选择均值来作为估计量对排序集抽样方法的优点和缺点进行分析,具有一定的参考意义。
二、排序集抽样方法的种类
(一)中位数排序集抽样方法
中位数排序集抽样方法在1997年被提出,具体的操作步骤:首先从样本总体中抽取样本组,容量为m,一共有m个样本组,按照变量从小到大的顺序进行排序。当m是偶数的时候,则从前面开始的m/2组选择样本组,次序为m/2,然后从后面开始的m/2组选择样本组,次序为(m+2)/2;当m是奇数的时候,则选择每个样本组的中位数,一共有m个样本测量对象。[3]
(二)极值排序集抽样方法
极值排序集抽样方法在1996年被提出,具体的抽样步骤:从样本总体中选择样本组,一共有m组,每个样本组容量为m,按照变量从小到大的顺序进行排序。当m是偶数的时候,则从前面的m/2组选择样本,选择样本组中最小的样本,然后从后面的m/2组选择最大的样本;当m是奇数的时候,则从前面的m-1/2组选择最小的样本,从后面的m-1/2组选择最大的样本,在前面m-1/2组和后面m-1/2组之间的中间组选择中位数。如此以来通过极值排序集抽样的方法获得m个测量样本。[1]
三、不同抽样方法下总体均值的比率估计方法
(一)简单随机抽样下估计总体均值的比率
假如目标变量为Y、辅助变量为(X,Y)属于一个二维总体,关系函数表示为f(X,Y),采用(Ux,Uy)表示均值。从样本总体中抽取随机样本,记录为(X1,Y1),(X2,Y2),…,(Xn,Yn),已知条件为总体均值Ux,变量的总体均值Uy比率估计为
Uysrs=Ysrs/Xxrs*Ux;
Ysrs=1/n∑Yi,Xsrs=1/n∑Xi表示样本均值。[5]根据相关文献证明,随机抽样方法对总体均值的比率进行估计具有无偏性。
(二)中位数排序集抽样下估计总体均值的比率
(1)根据上述中位数排序集抽样的方法抽取检测样本对象,当m为偶数的时候,排序集如下所示:

此时,测量样本记录为

总体均值为Uymrss=(Ymrss/Xmrss)Ux,Ymrss和Xmrss为样本均值。
(2)当m为奇数的时候,排序集如下所示:
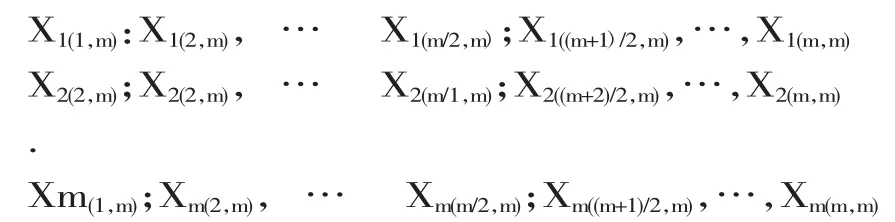
此时,测量样本记录为

样本均值为 Xmrss=1/n*∑Xi((n+1)/2),Ymrss=1/n∑Yi((n+1)2)
采用中位数排序集抽样方法对总体均值进行比率估计在整体上要比随机抽样方法对均值的估计要更为理想。[6]
综上,中位数排序集抽样方法是在基本排序集抽样方法的基础获得的改进方法。采用中位数排序集抽样方法对总体均值的比率进行估计,不仅具有基本排序集抽样方法的优点,具有渐进性,同时与随机抽样方法均值估计方法对比具有更高的统计效率。
[1]董晓芳,张良勇.基于中位数排序集抽样的非参数估计[J].数理统计与管理,2013(3):463-465.
[2]张建军,乔松珊.正态总体下参数的优化极大似然估计方法[J].统计与决策,2012(2):16-17.
[3]张良勇,董晓芳.基于中位数排序集抽样的符号检验[J].统计与决策,2013(14):76-78.
[4]董晓芳,崔利荣,张良勇.基于广义排序集样本的分位数估计[J].北京理工大学学报,2013(2):214-216.
[5]张建军,乔松珊.中位数排序集抽样下总体均值的比率估计方法[J].郑州大学学报(理学版),2015(1):47-48.
