基于Mathematica9.0设计机床补偿模型

朱琳琳

（辽宁机电职业技术学院 基础部， 辽宁 丹东 118009）

数控机床相对于传统机床，能够很好地解决复杂、精密、小批量、多品种的零件加工问题。在数控机床进行零件加工时，刀具会产生磨损，如果不进行必要的刀具轨迹补偿，对所加工零件的精度会产生很大影响。本文主要阐述利用Mathematica9.0的参数拟合功能构建刀具轨迹补偿模型，希望通过该模型拟合的数据来矫正数控机床刀具磨损轨迹，提高零件加工精度。[1]

一、模型设计思路

在构建磨损轨迹补偿模型时，我们充分考虑模型应具有一定的通用性，构建的模型针对不同刀具、不同机床时，只需要修改几组参数就能得到不同刀具磨损轨迹补偿数据与图像。[2]

基于上述考虑，我们将模型设计大致分为：数据录入、补偿模拟和拟合模型三个阶段。通过数据录入，我们修改其中的参数数据，就可以得到不同刀具磨损数据，让模型具有一定的通用性。通过补偿模拟，在考虑误差的情况下，我们能够准确计算刀具磨损程度并进行必要补偿。拟合模型，可以通过图像让我们更加直观地了解到需要补偿与实际磨损之间的差异。补偿模型为数控机床的编程工作提供必要的数据支持。[3]见图1。

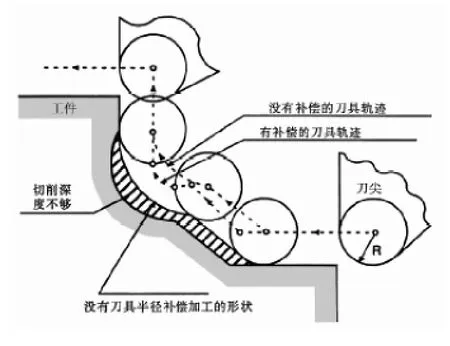
图1 刀具补偿示意图

二、刀具补偿模型设计

我们之所以选择Mathematica9.0作为模型设计平台，主要是其具有独特的参数设置与运算、函数拟合以及图像模拟等功能，它能够将这些功能进行良好的整合，这是其他数学软件很少具有的特点。[4]

（一）数据录入

为保证模型的通用性，在数据录入时，我们选择实验室数控机床实时加工零件过程进行录入，采用等时测量法，测试中每隔一小时测量一次刀具厚度（单位：mm），得到实验数据如表1所示。

表1 数控机床刀具磨损实时数据

依此表1进行数据录入得到图2，设计模型程序如下：[5]

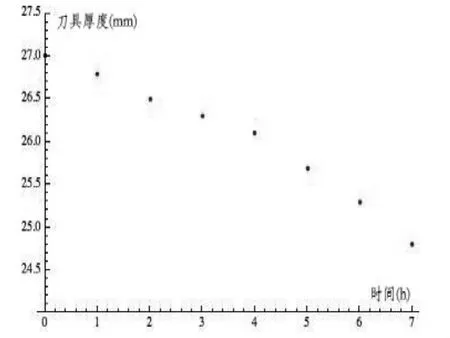
图2 刀具磨损数据图

从图2可以看出：这些点大致位于一条直线附近，我们拟合函数时可以认为y与t存在线性关系，可假设y=a+bt，其中a和b是未知常数。

（二）构建磨损补偿模拟

我们充分考虑了在实验中产生的误差，y与t的真实关系可以是=a+bt。对每一个自变量ti测定都会产生误差εi，所得到实际数据为yi=+εi。如果采用=a+bt，则误差如图3所示。

图3 补偿误差原理

数据的总误差平方和为：

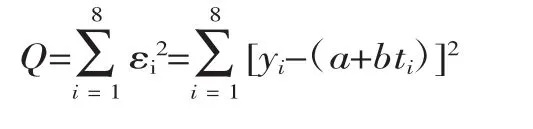
系数a与b的选择要使总误差平方和最小，刀具补偿才能达到理想状态，加工才能更精准。

参考上述误差估计，我们设计磨损补偿模型，此部分程序设计为：

（三）构建拟合模型

在得到上述补偿公式后，我们将上述补偿数据进行图像拟合。拟合后设计模型最终程序为如图4。[6]

图4 刀具补偿拟合图像

三、结束语

综上所述，利用Mathematica9.0设计的刀具补偿模型，能发挥软件自身参数运算和图像拟合的强大功能，精确运算需要补偿的数据。设计的补偿模型，能够研究如何精确控制数控机床刀具磨损补偿问题，提高加工零件的精度，提升数控机床编程效率。当然，由于该模型具有一定的通用性，只需修改相应参数就能得到其他刀具磨损参数，因此对于数控专业学生也可以作为一种实用教学模型，方便学生掌握专业知识。

［1］尤金D.Mathematica使用指南[M].北京：科学出版社，2012：113-145.

［2］蒂芬·沃尔夫雷姆.Mathematica全书[M].西安:西安交通大学出版社，2007：211-225.

［3］张雁.制图学[M].北京:高等教育出版社，2005：278-284.

［4］龙姝明,朱杰武,孙彦清,等.数学物理方法&Mathematica[M].西安：陕西人民教育出版社,2002.

［5］尤金 D.Mathematica使用指南[M].北京：科学出版社，2002.

［6］数学手册编写组.数学手册[M].北京：人民教育出版社，1979.