基于Mathematica9.0设计平面图形的几何变换
2016-03-20朱琳琳
朱琳琳
(辽宁机电职业技术学院 基础部, 辽宁 丹东 118009)
在工业设计制图中,当题目给出的原图需要进行位置调整时,我们可以将其作一定的变换,使问题得以解决,得到满意的制图设计。几何变换是一种重要的制图思想方法,它是一种以变化的、运动的观点来处理孤立的、离散的问题的思想,很好地领会这种思想实质,并能准确合理地使用,在设计制图中会收到奇效,也将有效地提高工业设计品质。[1]
一、几何变换基本原理
在函数定义中,如果有一种法则T,对平面点集D中的每个点A,都对应平面上唯一的一个点T(A),则 T 称为平面上的一个变换,T(A)称为点 A的像。[2]
几何变换是函数图像的一种自然推广。制图中的图像由点组成,因而平面上的变换T会将一个图形 C 变换到另一个图形 T(C),T(C)称为 C 的像,这就是T的几何变换。几何变换是Mathematica9.0辅助设计图形的重要技术之一,在工业设计制图中有着广泛的应用。[3]如图1。
二、几何变换设计模型
Mathematica9.0是一款科学计算软件,它很好地结合了图形系统、编程语言、文本系统与其他应用程序的高级链接。[3]几何变换模型,主要利用Mathematica9.0的图像模拟、进程演示等功能。
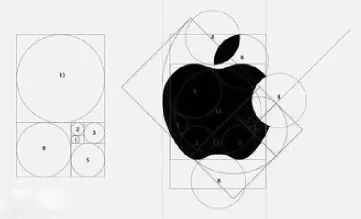
图1 商标设计
(一)平移模型
把函数y=f(x)变换为y=f(x+a),函数图像会向右移动a个单位,因此称a为水平位置参数。为方便模型设计,我们以此为例设计平移模型。[4]
据此设计程序为:

由上述结果绘制曲线,结果如图2所示。
(二)伸缩模型
把函数f(x)变换为f(s x),图像会发生压缩或者伸长,其作用是改变水平轴的刻度单位,我们称s为水平刻度参数。仍以此为例,设计伸缩模型。[5]
据此设计程序为:

由上述结果绘制曲线,结果如图3所示。
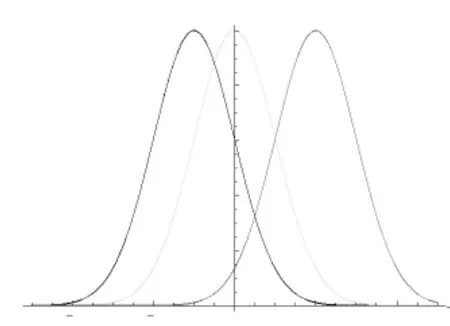
图2 平移模型图
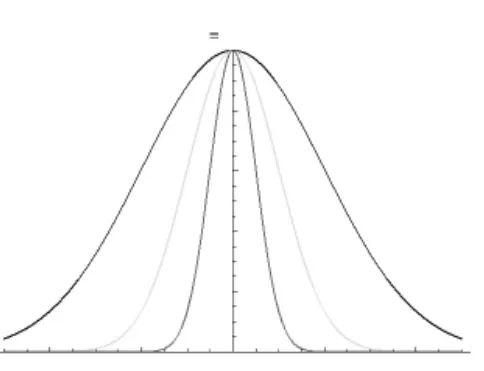
图3 伸缩模型图
(三)旋转模型
若图像以原点为中心旋转θ角,原来的坐标(x,y)变为新坐标(X,Y),旋转变换为:

由上述结果绘制曲线,结果如图4所示。
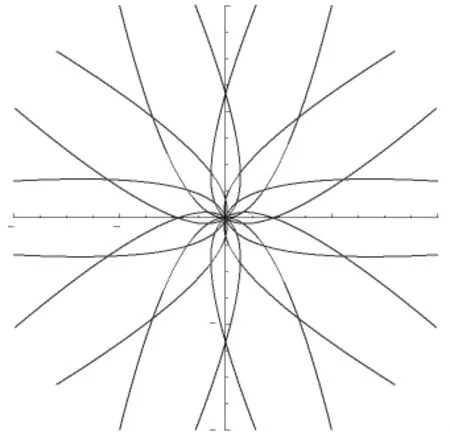
图4 旋转模型图
我们也可以对模型进行动态模拟,程序为:

由此动态模拟结果如图5所示。

图5 动态模拟结果图
三、结束语
综上所述,通过Mathematica9.0参数运算和图像等功能模拟函数图像的几何变换,让我们在了解函数几何变换的同时,还可对工业制图的设计技巧进行更深入研究,进而使工业制图设计更优化,也可使学生在学习工业制图课程时的教学更直观。
[1]尤金D.Mathematica使用指南[M].北京:科学出版社,2002:109-125.
[2]ANSLEY RF.Thewankel RC engine,design and performance[M].London:Liffe Books,Ltd,1970:125-168.
[3]蒂芬·沃尔夫雷姆.Mathematica全书[M].西安:西安交通大学出版社,2002:111-145.
[4]张雁.制图学[M].北京:高等教育出版社,1955:208-224.
[5]Jan P.Norbye.发动机设计与制图[M].华盛顿:奇尔顿图书出版社,1971:102-105.
[6]Martha L,Abell,James P.Braselton.Mathematica 的举例应用[M].纽约:埃森威尔图书出版社,2004:103-110.
