基于EMMS范式的离散模拟及其化工应用

徐骥，卢利强，葛蔚，李静海

（中国科学院过程工程研究所多相复杂系统国家重点实验室，北京 100190）



基于EMMS范式的离散模拟及其化工应用

徐骥，卢利强，葛蔚，李静海

（中国科学院过程工程研究所多相复杂系统国家重点实验室，北京 100190）

摘要：化工过程通常涉及化学、化工、过程系统工程3个层次，而每个层次又包含微尺度、介尺度和宏尺度，如化工层次的颗粒、颗粒团和反应器尺度。每个层次中的微尺度单元都自然适用离散模型，即通过跟踪每个单元的运动获得整个体系演化的宏观规律。但由于单元数量巨大，工程模拟往往依赖经过统计平均的连续介质模型。由此带来的精度问题，特别是忽略了介尺度结构的问题，随着对化工过程效率和绿色度等要求的提高而日渐突出。介绍了通过问题、模型、软件和硬件结构的一致性提升离散模拟的精度、能力和效率的方法、进展及其在复杂分子体系、颗粒流、气固流态化等方面的应用，展示了通过离散模拟实现虚拟过程工程的可能性。

关键词：离散模拟；EMMS范式；多相流；多尺度；颗粒；虚拟过程工程

2015-09-18收到初稿，2015-11-30收到修改稿。

联系人：葛蔚。第一作者：徐骥（1984—），男，副研究员。

Received date: 2015-09-18.

引 言

化工过程普遍涉及化学、化工和过程系统工程3个层次，如图1所示[1]。在每个层次中又可以划分为3个典型的尺度：微(单元)尺度、宏(系统)尺度以及两者之间的介尺度。微尺度用以描述系统中运动的最小时空单元，如考虑颗粒浓度分布时反应器中的单个颗粒；宏尺度代表所考虑的整个系统，如此时所涉及的反应器总体；介尺度则用以描述由微尺度单元在运动过程中形成的时空不均匀结构。由于介尺度结构的存在及其重要影响，宏尺度与微尺度间的关联往往难以借助既有的统计力学和热力学方法获得。因此无论对理论还是应用研究，从精确的微尺度模拟复现介尺度和宏尺度行为都是不可或缺的重要手段[1]。

然而，每一层次上单元尺度（上一层次的单元尺度同时也是下一层次的系统尺度）的研究方法，如分子动力学(molecular dynamics, MD)和离散单元法(discrete element method, DEM)，目前还存在计算规模小、速度慢、理想化假设较多和尺度间耦合困难等问题，难以满足上述需求。近年来的研究表明，通过保持问题、模型、软件和硬件结构的一致性，即EMMS范式[2]，可以极大地提高离散模拟的精度、能力和效率(ACE, 即accuracy, capability, efficiency)[3-4]。并可能带来以交互与实时模拟，及其与实验、测量、控制及可视化等系统紧密耦合为特征的化工模拟新模式，即虚拟过程工程(virtual process engineering, VPE)。

本文将重点介绍本研究团队在上述EMMS范式下建立大规模高精度离散能力的整体思路，所建立的模拟平台的基本框架、功能和性能，并介绍其在复杂分子体系、颗粒流和气固流态化等领域的典型应用。还将介绍通过多尺度离散模拟构建VPE系统的初步尝试，最后将展望离散模拟方法和VPE的发展方向。

图1 化学工程涉及的3个层次和其中的多尺度结构[1]Fig. 1 Multi-level, multi-scale hierarchy of chemical engineering[1]

1 基于EMMS范式的离散模拟

能量最小多尺度(energy-minimization multiscale, EMMS)模型最早针对气固流态化系统提出[5-6]，通过稀密相的划分和稳定性条件的引入封闭了含介尺度结构参数的多尺度流动模型，现已扩展应用于气液、气液固和湍流等体系[7-8]，由此形成了以不同的控制机制在竞争中协调为核心的稳定性条件的一般表达[1,9]，并通过拟颗粒模拟(pseudo-particle modeling, PPM)[10]等离散模拟方法在多个系统中得以验证[11-12]。在此过程中，通过抽象不同离散模拟方法的共性[13-14]，逐步建立了其通用模拟平台[15]，进而提出了EMMS范式，即通过离散模拟与介尺度模型结合提高计算精度与效率[2]。该范式的核心内容包括两方面：一是从整体到局部、从分布到演化的建模方法；二是保持问题、模型、软件和硬件结构一致性的计算模式[3]。基于EMMS范式可以建立更精确、快速和高效的模拟方法。下面分别从模型、软件和硬件3方面阐述该平台的构建思路，并说明如何在每个方面描述或建立其多尺度结构。

1.1 多尺度离散模型的构建

尽管化工过程涉及不同层次的多个尺度(图1)，但对每个尺度几乎都能建立相应的离散模型。这是多尺度离散模拟的第1层含义。首先在各层次的单元尺度，可以建立直观而自然的离散模型。在原子和分子尺度，从经典力学的角度看原子间主要存在两体或多体间的有势作用，可以用MD模型较好地描述[16]；而在颗粒尺度，宏观的颗粒间碰撞、摩擦和变形等也可以最终分解为离散点间的作用，以DEM[17]建模；在反应器尺度，过程系统工程中也广泛采用各单元设备模型，通过输入输出参量的耦合建立离散的网络模型。其次，为了解决实际系统中单元数量巨大、计算规模受限的问题，还可以在上述模型基础上发展相应的粗粒化方法。如考虑分子团之间能量转化的耗散粒子动力学(dissipative particle dynamics, DPD)[18]模型，和对原子/分子间碰撞做统计(随机)处理的直接模拟Monte Carlo (direct simulation Monte Carlo, DSMC[19])与拟颗粒模拟[10]。而从颗粒尺度出发，也相应地存在粗颗粒(coarse grain model)[20-21]和网格中的粒子(particle in cell, PIC)[22]等模型。这些模型的存在为构建完整的化工过程多尺度离散模拟体系提供了可能。

如图2左侧模型(modeling)部分所示，多尺度离散模拟的另一层含义是在某一尺度的离散单元间可以存在不同尺度的作用，它们可以包括如下作用。

（1）近程作用(short range interactions)，如MD中分子间的范德华力(van der Waals forces)以及DEM中颗粒间的接触作用或碰撞(contacts/ collisions)等，也包括各自独立的单元状态更新(updating)等。

（2）长程关联(long range interactions)，如复杂的聚合物[24]和生物[25]分子中多个原子间的约束作用(constraints)和静电力中的长程部分(long range electrostatic forces)[26]。而非平衡态体系的建模还涉及外场作用(external forces)[25]。类似地，在黏性颗粒、湿颗粒及颗粒流体系统中也存在静电等长程力和流体流动等外场作用。而在复杂形状颗粒的组合模型中，其成员颗粒间相对位置的控制也属约束作用。

（3）全局约束(global constraints)，在非平衡过程中，离散单元间在稳定性条件的驱动下通过上述短程和长程作用还会形成全局与介尺度结构(global distribution)。尽管单纯由动力学角度也可以从底层描述这些结构的形成，但从计算角度看，直接利用这些结构的特征首先从总体上分布和约束单元的演化则可以大大减少计算量，提高模拟精度和速度。因此在计算中将全局约束也看作一种独立的作用，并以此优化计算的初始条件与负载平衡(load balance)操作等。

这种多尺度作用模式的存在就要求在离散模拟的软件和计算硬件设计中同样考虑多尺度结构和逻辑，而这也正是EMMS范式的核心思想之一。

1.2 软件框架

尽管不同时空尺度的离散模拟方法具有各自的特点，但从计算角度分析，计算量最大的部分一般是单元间的相互作用，尤其是近程作用，通常会消耗50%～70%的计算量[27]。而这种近程作用在算法上的共性为建立离散模拟的统一软件平台提供了可能[13, 15, 28-29]。而在考虑了模拟对象的多尺度结构与稳定性约束后，体现EMMS范式的多尺度离散模拟平台为实现虚拟过程提供了有效途径。

图2 基于EMMS范式的离散模拟平台三层结构[23]Fig. 2 Three layers of discrete simulation platform based on EMMS paradigm[23]

根据这一思路，将离散模拟方法的软件实现分为3个层级，如图2中间“软件”(software)部分所示。软件的上层部分对应模型的全局约束，负责软件运行的整体控制。包括优化模拟的初场分布；软件运行过程中的负载均衡，即减少大规模并行计算时由于计算量分布不均造成相互等待和计算效率的损失。该类计算大多属于全局优化问题，往往涉及矩阵和图的全局操作并涉及几乎所有并行进程，计算复杂度高。但其调用频率较低、计算量较小，主要集中在计算开始时，因而由结构复杂而数量较少的上层计算硬件执行。

中层部分的软件对应模型中的长程关联部分的计算，其计算量适中但是操作比较复杂，而且往往涉及不同节点间大量的数据交换。在目前常见的分布式并行计算系统中，节点间的通信量随着节点数目的增加迅速增大，严重限制了大规模并行计算的效率。如MD中常用的约束(constraints)算法SHAKE[30]涉及迭代计算，通常需要多次并行通信；而LINCS[31]方法尽管无须迭代，但也受到并行通信速率的限制。而计算长程静电作用的PME (Particle Mesh Ewald)方法[32-33]则涉及全局通信。外场作用(external forces)为与其他方法（如连续介质模型）预留了耦合接口，从而将离散模拟拓展至多相流等体系，但它通常也涉及复杂的通信和数据交换。由此可见中层软件对并行度和通信速率与带宽等具有较高要求。

软件的底层部分负责处理模型中的近程作用(short range interactions)。因为涉及系统演化的细节，需要求解每一个单元的运动，其计算量通常最大。但从算法设计和软件实现角度分析，该部分模型的计算操作相对简单，主要是对大量常微分方程的数值积分，具有良好的数据局部性和可加性，并且经常可以对大量数据执行相同的操作。MD中范德华力(van der Waals forces)和LJ(Lennard-Jones) 势[34]，以及DEM中描述颗粒间碰撞(contacts/ collisions)的Hertz作用[35]等的计算均具有这样的特点。而运动单元的迭代更新(updating)由于通常不涉及数据通信也具有此特点，这些特点可以保证大规模并行计算的高效性。

1.3 硬件系统

根据上述软件实现的特点，建立了相应的基于EMMS范式的多尺度硬件体系结构[36]。这里以近年来构建的多尺度超级计算系统Mole-8.5E[37-39]为例，介绍该体系结构的一种初步实现。如图2右侧的硬件(hardware)部分所示，该系统的上层和中层节点采用CPU进行复杂的计算和通信；同时中层和底层的节点分别采用MIC (many integrated core)[40]和GPU[41]提高计算能力。这3层结构分别对应于多指令多数据多核 (multiple instruction multiple data (MIMD) multicore)、多指令多数据众核 (MIMD manycore) 和单指令多数据众核(single instruction multiple data (SIMD) manycore) 3类处理器架构，也分别对应了软件的三层结构中的操作。与传统上单纯基于CPU的超级计算系统相比，即使对于通用计算，它在效费比和效能比上也具备显著的优势[38]，而对EMMS方式下的离散模拟则可获得数量级的提升[36]。目前该系统已在一系列基础和工业应用研究中得到成功应用。

2 平台实现

除了构建基于EMMS范式的离散模拟方法与软硬件框架，为了在化工基础研究与工业应用中更好地发挥其能力，还应进一步建立系统的模拟平台。该平台应具备完善的前后处理能力和良好的易用性，并能与其他方法和软件耦合或建立高效方便的接口。近年来一个覆盖图1中从分子到反应器5个尺度的统一的离散模拟平台正在构建中，并已经实现了对一些体系的离散模拟，包括材料[42]、生物大分子[43]、颗粒流[44]、气固体系[21]、液固体系[45]等方面。其主要的技术和功能特点如下。

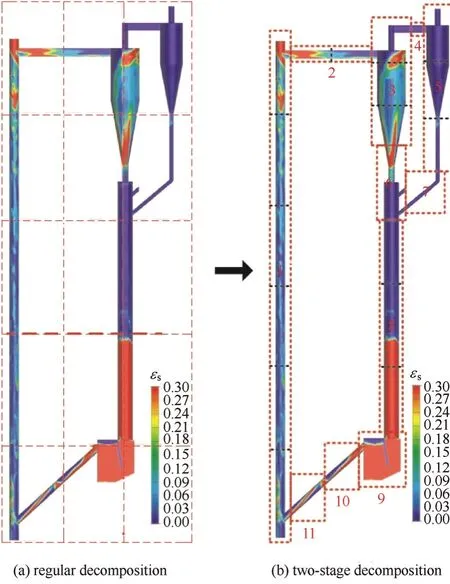
图3 非规则模拟区域的并行分割Fig. 3 Parallel decomposition of irregular simulation domains

（1）为适应实际化工装置的结构复杂性，在实现近程、长程、约束、外场作用等模型的CPU、GPU或MIC计算[21, 24, 42, 45-48]的基础上还发展了两级区域分解并行算法。如图3所示的循环流化床，实际需要模拟的区域仅为流化床内部，而常用并行算法对流化床占据的整体空间进行划分 [图3(a)]，浪费了大量计算资源。新算法[图3(b)]首先根据装置的有效区域划分第1级子区域[图3(b)中的1～11]，再根据它们各自的颗粒分布进行2级划分，实现了计算资源的有效利用。由于区域分割与负载平衡等操作可以在顶层节点执行，这样的精细分割并不会对计算本身产生较大影响，保证了平台的效率和实用性。

（2）为处理实际化工过程中离散单元的复杂结构，实现了简单形状单元组合[49]、多边形或样条曲线(面)近似、解析表达等非规则几何描述方式。由此可以处理如填料、催化剂、矿石以及聚合物和生物大分子等多种复杂单元。

（3）鉴于多种处理器及通信模式耦合的多尺度计算中数据交换受到一些瓶颈环节的制约(如GPU-CPU及GPU-GPU之间)，采用了多种计算与通信、计算与存储访问以及不同部分的计算间重叠的优化设计，最大限度缩短了计算中的等待时间，提高了并行效率[50]。

（4）为满足多相体系模拟的需求，离散模拟平台可以作为固相求解器与求解流体等其他相的方法或软件耦合，形成离散-连续耦合模拟平台。目前支持的流体求解方法包括有限体积法(finite volume method)、格子Boltzmann方法(lattice Boltzmann method, LBM)，耦合方法包括颗粒轨道模型(discrete particle method, DPM)和浸入边界法 (immersed boundary method, IBM)等，可耦合的软件有Fluent和OpenFOAM等。

目前，离散模拟平台中的MD和DEM模块已经形成注册软件[51-53]，其中DEM模块DEMms已开放使用(详见http://159.226.63.40/demms[53])。借助团队面向多尺度离散模拟建立的Petaflops级高效能超级计算系统Mole-8.5E[37-39]，离散模拟平台已能处理单元数高达109～1011量级的工业体系，并可达1010步/秒以上的粒子更新速率。在对聚合物、硅材料和颗粒混合等过程的模拟中其计算效能可达到原先基于CPU的相应软件的10倍左右[24, 46, 50, 54-55]。

3 应 用

基于EMMS范式的离散模拟及其软硬件平台的建立为它在基础研究以及工艺、过程和装备开发中的应用提供了条件。下面介绍的一些典型实例表明离散模拟已经能够突破理论与实验室研究的范畴，成为一种有效的工业和工程模拟手段。

3.1 材料和生物体系的MD模拟

图4 材料和生物体系的MD模拟Fig. 4 MD simulation of material and biological systems

离散模拟平台拓展了MD方法的模拟能力，从而能够直接从原子尺度进行材料、生物领域内一些宏观体系的模拟。如图4(a)所示，在硅纳米线的导热研究中，通过CPU与GPU耦合计算实现了从微观（10-10m）模型到宏观现象（10-3m）的直接计算，完整复现了其尺度效应。模拟体系含有约1100亿个原子，跨越了7个空间尺度量级，相对之前的CPU计算加速比达到650多倍，并实现了国内首个Petaflops级的应用计算，计算峰值达到单精度1.87 Petaflops[42]。在生物体系的研究中，实现了完整流感病毒（H1N1）在溶液中的动态结构的模拟，体系含有3亿多个原子，计算速度最高可达相同进程数通用CPU软件的32.6倍[54]，是当时生物体系模拟中规模最大、结构最复杂的原子层次模拟，有望为抗流感药物的设计提供有力工具。

3.2 颗粒流模拟

颗粒物料是化工过程中最常见的原料和产品之一，因此对颗粒的输送、混合、传热等过程的模拟具有广泛的工业应用。同时，由于对此类体系还缺乏有效的介尺度模型和连续介质描述，其理论研究也是多个领域关注的热点[57]，而模拟将为此提供有力手段。DEM是目前颗粒体系模拟的最主要方法。对于简单的光滑颗粒，在DEM模拟中已能实现工业规模的滚筒混合或输送设备的准实时模拟。如对一个长13.5 m、直径1.5 m、含960万个毫米级颗粒的工业规模滚筒混合器的模拟[46]，采用30 块C2050 GPUs，约能达到物理演化速度的1/60。

利用这样的能力，实现了某工艺中试装置的螺旋混合-输送器在不同结构和操作参数下的混合指标[58]与停留时间分布[59]的模拟。其中结构参数包括螺距、进料口位置和输送器长度等，而操作条件包括转速和物料添加速率等。另外通过计算颗粒间在接触面上的导热[60]还可获得其中的温度分布，图5为一组模拟结果的快照（在http://159.226.63.40/ demms上可看到其动态演示）。模拟结果与可测量的出口粒径分布等实验结果符合良好，而模拟还能提供实验中难以测量的内部动态过程，从而为了解混合机理、优化装置结构等提供重要参考。与实验相比，其费用低、速度快、效果好的优势非常突出。

3.3 两相流的直接数值模拟

为了深入了解多相反应器中介尺度结构形成的底层机理，以及微化工和过程强化等领域精细的流动、传递和反应过程，能够精确解析每个颗粒周围流场的直接数值模拟 (direct numerical simulation, DNS)[47, 61-62]已成为重要的研究手段。该模拟几乎不依赖经验模型，准确性和可靠性都明显优于其他模拟方法，但是其计算量巨大，严重限制了其适用范围。前述离散模拟平台以及多尺度超级计算系统的应用显著拓展了DNS的时间和空间尺度，为研究更接近于真实的化工过程提供了可能。

在图6(a)、(b)的气固两相流的模拟中，应用LBM求解气相[63]，DEM求解固相颗粒，实现了宏观体系的DNS[47]，模拟的空间尺度达到了10-1m。在11.5 cm×46 cm的二维体系模拟中，颗粒数最大超过100万个 [图6(a)]；在0.384 cm×1.512 cm× 0.384 cm的三维体系模拟中，颗粒数超过10万个[图6(b)]，而之前典型的DNS颗粒数在103量级[65-67]。其计算速度在单块C2050 GPU上即达到了E5520 CPU单核的60多倍，而且具有较好的并行性，拓展到672块GPU时仍然具有近乎线性的加速比[2]。

图5 颗粒在螺旋输送器中的混合与温度分布Fig. 5 Particle mixing and temperature distribution in screw conveyor

在图6(c)的搅拌釜模拟中，应用有限差分方法并结合IBM[68]和大涡模拟(large eddy simulation, LES)[69]求解流体，DEM处理固相颗粒，已经可以模拟实验室规模的搅拌反应釜。如图6(c)所示，该搅拌釜外形尺寸为f 48 mm×48 mm，具有圆柱形壁面，内置一套六叶斜桨，并含4731个1.5 mm颗粒。在5123的流体网格下可以获得釜内流动与传热过程的细节，并考察如有效曳力系数和传热系数等对工业反应釜设计至关重要的参数。目前在尝试更大规模的搅拌反应釜模拟，颗粒数达到136300个，网格数达13443≈2.4×109个，使用512块GPU计算时，估计能在1个月内获得稳态结果[64]。

3.4 气固反应器的离散颗粒模拟

在面向工业装置的多相体系模拟中目前普遍采用连续介质方法，如颗粒流体系统的双流体模型(two-fluid model, TFM)[70-71]等。但由于固相作为连续介质处理的困难，特别是忽视介尺度结构带来的误差，其模拟精度与工程需求还有很大差距[72]。现在随着离散模拟速度与精度的提高，特别是一系列粗粒化模型的提出[21]，颗粒离散模拟与流体连续介质模拟相结合的DPM有望带来很大改观[20, 21, 72-74]。

如通过流动开源求解器OpenFOAM与离散模拟平台的耦合，实现了如图7(a)所示的某气固反应器中颗粒停留时间分布(residence time distribution, RTD)的DPM模拟。其计算速度达到650 s·d-1，模拟的物理时间达6800 s。而之前双流体模拟的物理时间也仅为几十秒到几分钟[75]，且很难准确计算RTD。根据Kunii等[76]的分析，单一尺寸颗粒形成的密相流化床中颗粒近似处于完全混合状态。而比较模拟结果与全混流时的RTD[图7(b)]可以发现两者确能很好符合。

3.5 虚拟过程工程的初步示范

以上述高效离散和离散-连续耦合模拟方法和平台为基础，已能建立VPE的演示系统，即将计算机模拟与在线控制、实时数据处理相结合，实现高精度的化工过程模拟，实时、在线地比较模拟与实验数据，并动态观察结果[77]。VPE将从模拟角度改变化工过程的研发模式，帮助工程人员更精确、高效地实现化工过程的预测、优化、仿真和培训[2]。

图6 两相流的直接数值模拟Fig. 6 DNS of two-phase flow

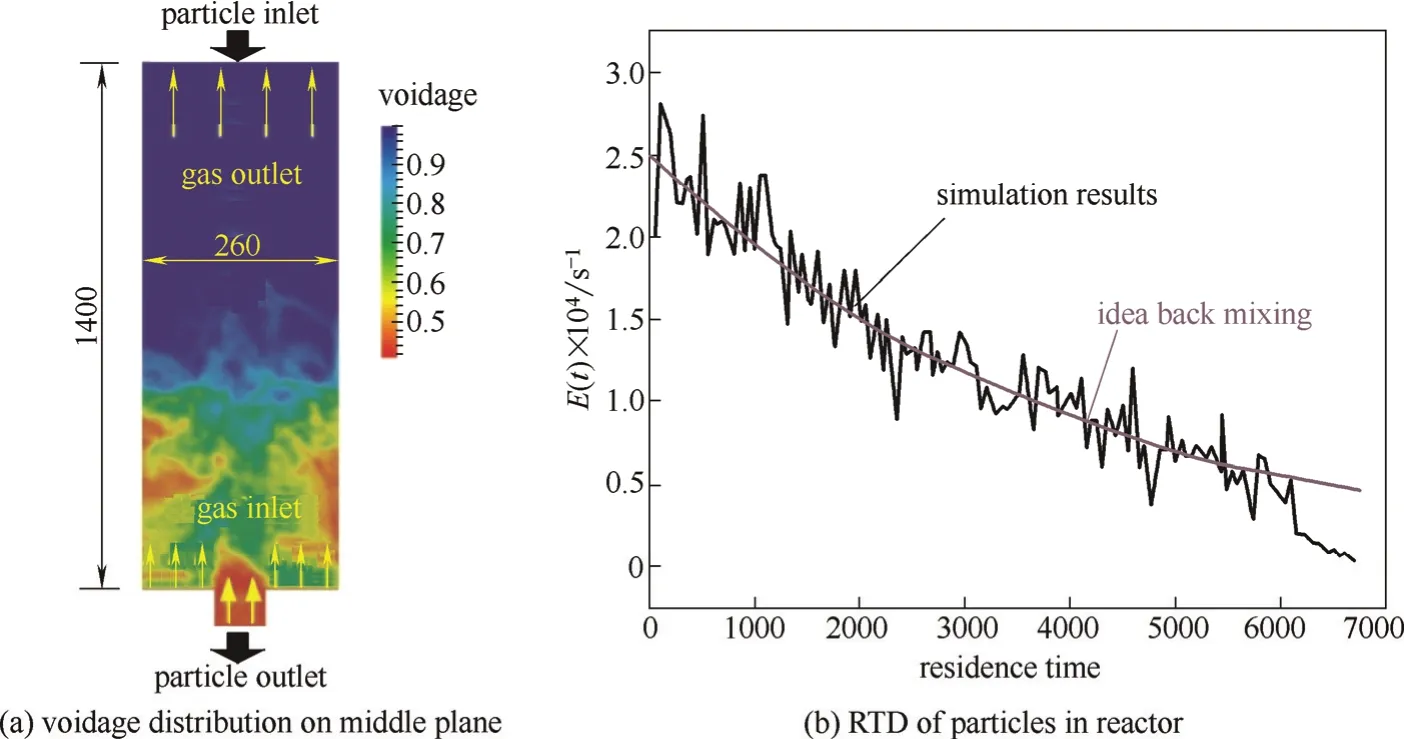
图7 气固反应器的DPM模拟Fig.7 DPM simulation of a gas-solid reactor

首先实现了两股射流体系（图8）的VPE演示，其模拟速度可完全达到实际物理演化速度[78]。在模拟过程中，可以在线改变操作参数，如射流速度、方向、颗粒属性等，实时地获得模拟结果，并根据模拟结果进一步优化操作条件。事实上，除了作为VPE的演示，该系统还可用于如多喷嘴撞击流反应器[79]及颗粒混合过程等的研究中。

在气固循环流化床(circulating fluidized bed, CFB)反应器中，尝试了提升管的VPE[21, 23]。如图9所示，用户通过拖动装置图上的红色矩形框可以调整显示区域（右侧当前显示的是提升管底部的模拟结果）。右下方为速度控制、显示窗口，可以拖动滑动条来减小或增大操作气速，左上方为系统统计的轴向空隙率的实时分布。该模拟采用21万个粗颗粒，在12个进程并行时可以达到1/40的实时速度，在线可视化速度为5帧/秒。如图10所示，其轴向[图10(a)]和全床瞬时空隙率分布[图10(b)]、底部4 m的床层内颗粒的瞬时分布[图10(c)]和不同高度上径向的空隙率分布[图10(d)]均能与实验数据吻合并且复现合理的颗粒团聚现象。尽管离实现完整的VPE系统其效果仍有较大差距，但对于教学和培训等目的，该系统已能发挥实际作用。

图8 两股颗粒流实时模拟[78]Fig. 8 Snapshot from realtime simulation of two streams of granular flows[78]

4 总结与展望

本文的论述表明基于EMMS范式的多尺度离散模拟通过保证问题、模型与软硬件的结构一致性可以显著提高模拟的精度、速度与效率，从而为实际化工过程的模拟带来新的可能，并推动虚拟过程工程的最终实现。为实现这一目标，今后的研究应集中于以下几方面。

（1）离散模拟在实际应用中还需解决很多问题，包括非规则单元结构与变形的更高效处理，以及单元间的聚并与破碎等动态过程的处理。对于运动与传热、传质、反应等过程的耦合，目前的处理大多借鉴了连续介质模型，还缺乏能充分利用离散单元特性的简便而高效的方法，值得深入研究。

（2）在通过模型降低离散模拟的计算量方面，从离散角度深入研究介尺度结构的形成机理，从而建立离散模拟粗粒化的通用理论，进而构建多尺度的离散模拟模型，是一条有效途径。尽管近些年计算能力的飞速发展极大地拓展了离散模拟的时空尺度，但与许多化工过程的模拟需求仍相去甚远，粗粒化是降低计算量的最有效途径之一[21, 80]。粗粒化的尺度是该方法的核心问题，尺度过小则加速效果不明显；尺度过大，特别是超过了介尺度结构的特征尺度，则会引起较大的失真。因此，基于介尺度科学的粗粒化方法应得到重视，而其本身也是统计力学与热力学的前沿课题。

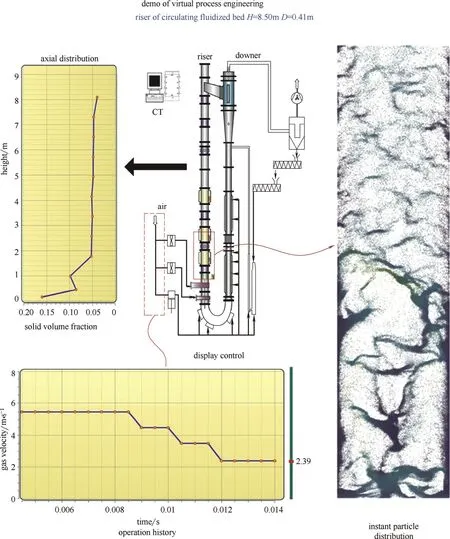
图9 气固循环流化床的虚拟过程工程演示[23]Fig. 9 Demo of VPE for gas-solid CFB riser[23]

（3）在提高离散模拟的计算能力方面，未来超级计算机的发展将与应用紧密结合，在归纳计算对象共同结构和逻辑特征的基础上，实现问题、模型、软件、硬件结构和逻辑一致性将是最合理的发展方向，一旦取得突破将对广泛的科学和工程领域产生重要影响，但这需要计算机科学和工程科学的无缝结合。多尺度离散模拟本身已覆盖了宽广的应用领域，而其软硬件设计又符合统一的框架，这就为其专用计算平台的建立提供了必要与可能。目前专门针对MD设计的Anton[81-82]等专用系统的应用面还较狭窄，而Mole-8.5E系统目前的实现还在节点层次，借用了既有的处理芯片。如何从更底层的芯片和软件体系结构设计出发建立更高效和通用的计算平台是实现虚拟过程等长远目标的技术保证。

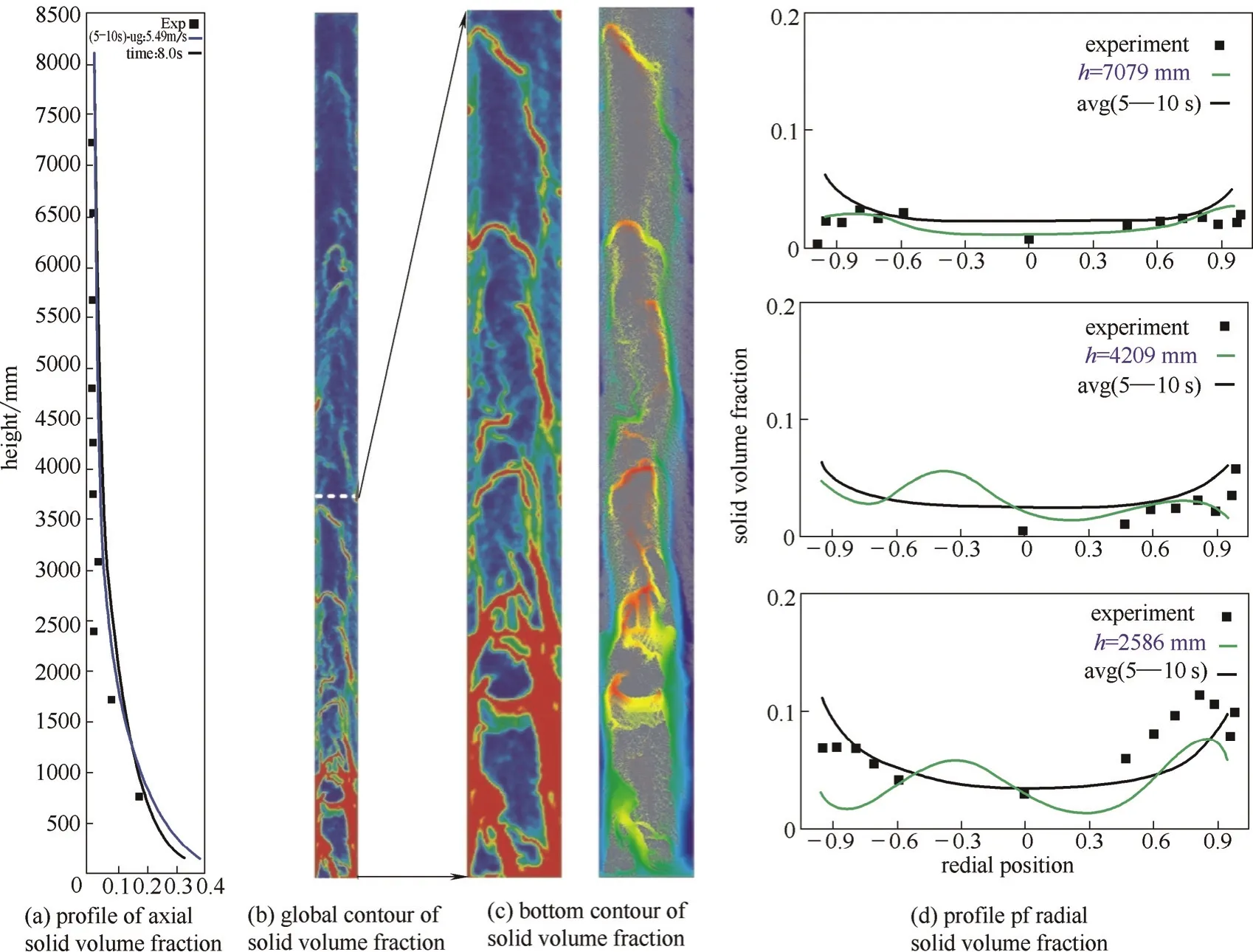
图10 VPE模拟结果与实验数据的对比Fig. 10 Comparison of the VPE simulation results with experimental measurements

（4）在拓展离散模拟的应用方面，与连续介质模型的耦合是重要的手段之一，而两者的变量间的映射是没有很好地解决但又对模拟精度与效率有重要影响的问题。这方面的研究涉及从离散到连续的统计力学处理，以及从连续到离散的约束条件等深刻的理论问题，需要多学科的交叉研究。

EMMS范式与多尺度离散模拟的发展已经预示了VPE的可能性，但其最终实现还有赖于介尺度科学、多尺度建模和模拟软硬件系统的极大发展。同时也需要与实验和测量技术、可视化与控制技术、人机交互技术等的有效集成。这将是一个多学科和多种技术交叉融合的前沿领域，需要不同学科的长期密切的合作才能实现。尽管还有这些艰巨的工作，多尺度离散模拟最终将带来化学工程基础研究与应用开发手段的革命性变化，为建立更高效而绿色的化学工业做出贡献[77]。

致谢 感谢狄升斌在液固搅拌釜直接数值模拟、戚华彪在颗粒流模拟方面提供的帮助。感谢国家杰出青年基金（21225628）、重点基金（91434201），中国科学院重大专项（XDA07080102）以及交叉研究团队的资助。

References

[1] LI J H, GE W, KWAUK M. Meso-scale phenomena from compromise—a common challenge, not only for chemical engineering [J/OL]. http://arxiv.org/abs/0912.5407.

[2] GE W, WANG W, YANG N, et al. Meso-scale oriented simulation towards virtual process engineering (VPE)—the EMMS Paradigm [J]. Chemical Engineering Science, 2011, 66(19): 4426-4458.

[3] 李静海, 黄文来. 探索介科学：竞争中的协调原理[M]. 北京: 科学出版社, 2014. LI J H, HUANG W L. Towards Mesoscience: the Principle of Compromise in Competition[M]. Beijing: Science Press, 2014.

[4] LI J H, HUANG W L. Towards Mesoscience: the Principle of Compromise in Competition[M]. Berlin: Springer, 2014.

[5] LI J H, TUNG Y, KWAUK M. Method of energy minimization in multi-scale modeling of particle-fluid two-phase flow[M]// BASU P, LARGE J F. Circulating Fluidized Bed Technology. Pergamon, 1988:89-103.

[6] 李静海. 两相流多尺度作用模型和能量最小方法[D]. 北京: 中国科学院化工冶金研究所, 1987. LI J H. Multi-scale modeling and method of energy minimization in two-phase flow [D]. Beijing: Institute of Chemical Metallurgy, Chinese Academy of Sciences, 1987.

[7] LI J H, ZHANG J Y, GE W, et al. A simple variational criterion for turbulent flow in pipe [J]. Chemical Engineering Science, 1999, 54(8): 1151-1154.

[8] GE W, CHEN F G, GAO J, et al. Analytical multi-scale method for multi-phase complex systems in process engineering—bridging reductionism and holism [J]. Chemical Engineering Science, 2007, 62(13): 3346-3377.

[9] LI J H, GE W, WANG W, et al. Focusing on the meso-scales of multi-scale phenomena—in search for a new paradigm in chemical engineering [J]. Particuology, 2010, 8(6): 634-639.

[10] GE W, LI J H. Pseudo-particle approach to hydrodynamics of gas/solid two-phase flow[C]// Proceedings of the 5th International Conference on Circulating Fluidized Bed. Beijing: Science Press, 1996: 260-265.

[11] GE W, LI J H. Macro-scale phenomena reproduced in microscopic systems—pseudo-particle modeling of fluidization [J]. Chemical Engineering Science, 2003, 58(8): 1565-1585.

[12] GE W, LI J H. Simulation of particle-fluid systems with macro-scale pseudo-particle modeling [J]. Powder Technology, 2003, 137(1/2): 99-108.

[13] GE W, LI J H. Conceptual model for massive parallel computing of discrete systems with local interactions [J]. Computers and Applied Chemistry, 2000, 17(5): 385-388.

[14] GE W, MA J S, ZHANG J Y, et al. Particle methods for multiscale simulation of complex flows [J]. Chinese Science Bulletin, 2005, 50(11): 1057-1069.

[15] 唐德祥. 粒子模拟并行计算通用平台的设计与初步应用[D]. 北京:中国科学院过程工程研究所, 2005. TANG D X. A general method of parallel computation for particle methods and its preliminary applications[D]. Beijing: Institue of Process Engineering, Chinese Academy of Sciences, 2005.

[16] ALDER B J, WAINWRIGHT T E. Molecular Dynamics by Electronic Computers[M]. New York: Wiley, 1956.

[17] CUNDALL P A, STRACK O D L. A discrete numerical-model for granular assemblies [J]. Geotechnique, 1979, 29(1): 47-65.

[18] HOOGERBRUGGE P J, KOELMAN J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics [J]. EPL (Europhysics Letters), 1992, 19(3): 155-160.

[19] BIRD G A. Approach to translational equilibrium in a rigid sphere gas [J]. Physics of Fluids, 1963, 6(10): 1518-1519.

[20] TSUJI Y, TANAKA T, ISHIDA T. Lagrangian numerical-simulation of plug flow of cohesionless particles in a horizontal pipe [J]. Powder Technology, 1992, 71(3): 239-250.

[21] LU L Q, XU J, GE W, et al. EMMS-based discrete particle method (EMMS-DPM) for simulation of gas-solid flows [J]. Chemical Engineering Science, 2014, 120: 67-87.

[22] ANDREWS M J, OROURKE P J. The multiphase particle-in-cell (MP-PIC) method for dense particulate flows [J]. International Journal of Multiphase Flow, 1996, 22(2): 379-402.

[23] GE W, LU L Q, LIU S W, et al. Multiscale discrete supercomputing – a game changer for process simulation? [J]. Chemical Engineering & Technology, 2015, 38(4): 575-584.

[24] XU J, REN Y, GE W, et al. Molecular dynamics simulation of macromolecules using graphics processing unit [J]. Molecular Simulation, 2010, 36(14): 1131-1140.

[25] XU J, HAN M Z, REN Y, et al. The principle of compromise in competition: exploring stability condition of protein folding [J]. Science Bulletin, 2015, 60(1): 76-85.

[26] PERUTZ M. Electrostatic effects in proteins [J]. Science, 1978, 201(4362): 1187-1191.

[27] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics [J]. Journal of Computational Physics, 1995, 117(1): 1-19.

[28] GE W, LI J H. General approach for discrete simulation of complex systems [J]. Chinese Science Bulletin, 2002, 47(14): 1172-1175.

[29] 王小伟. 可叠加近程作用粒子系统模拟的并行计算框架及通用化研究[D]. 北京: 中国科学院过程工程研究所, 2008. WANG X W. A framework for parallel simulation of particle systems with pair-additive local interactions — toward a general approach[D]. Beijing: Institute of Process Engineering, Chinese Academy of Sciences, 2008.

[30] RYCKAERT J-P, CICCOTTI G, BERENDSEN H J C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes [J]. Journal of Computational Physics, 1977, 23(3): 327-341.

[31] HESS B, BEKKER H, BERENDSEN H J C, et al. LINCS: a linear constraint solver for molecular simulations [J]. Journal of Computational Chemistry, 1997, 18(12): 1463-1472.

[32] DARDEN T, YORK D, PEDERSEN L. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems [J]. The Journal of Chemical Physics, 1993, 98(12): 10089-10092.

[33] ESSMANN U, PERERA L, BERKOWITZ M, et al. A smooth particle mesh Ewald method [J]. The Journal of Chemical Physics, 1995, 103(19): 8577-8593.

[34] LENNARD-JONES J E. Cohesion [J]. Proceedings of the Physical Society, 1931, 43(5): 461-482.

[35] HERTZ H. Miscellaneous Papers [M]. JONES D E, SCHOTT G A, trans. London, UK: Macmillan, 1896.

[36] LI B, ZHOU G Z, GE W, et al. A multi-scale architecture for multi-scale simulation and its application to gas-solid flows [J]. Particuology, 2014, 15(0): 160-169.

[37] WANG X W, GE W. The Mole-8.5 Supercomputing System[M]. Chapman & Hall/CRC, 2013.

[38] WANG X W, GE W, HE X F, et al. Development and application of a HPC system for multi-scale discrete simulation-Mole-8.5[C]// International Supercomputing Conference. Germany, 2010.

[39] GE W, XU J, XIONG Q G, et al. Multi-scale Continuum-Particle Simulation on CPU–GPU Hybrid Supercomputer[M]. Heidelberg, Berlin: Springer, 2013.

[40] Intel. Molecular dynamics optimization on Intel® many integrated core archi-tecture (Intel® MIC)[OL]. 2013. http://software. intel.com/en-us/articles/molecular-dynamics -optimization-on -intel -many-integrated- core-architecture-intel-mic

[41] NVIDIA CUDA. Compute Unified Device Architecture-CUDA Programming Guide.[M]. Santa Clara, CA: 2006.

[42] HOU C F, XU J, WANG P, et al. Petascale molecular dynamics simulation of crystalline silicon on Tianhe-1A [J]. InternationalJournal of High Performance Computing Applications, 2013, 27(3): 307-317.

[43] 徐骥. GPU加速度的大分子体系分子动力学方法——实现与应用[D]. 北京: 中国科学院过程工程研究所, 2012. XU J. GPU accelerated MD simulation for macromolecular systems[D]. Beijing: Institute of Process Engineering, Chinese Academy of Sciences, 2012.

[44] QI H B, XU J, ZHOU G Z, et al. Numerical investigation of granular flow similarity in rotating drums [J]. Particuology, 2015, 22(0): 119-127.

[45] DI S B, GE W. Simulation of dynamic fluid-solid interactions with an improved direct-forcing immersed boundary method [J]. Particuology, 2015, 18: 22-34.

[46] XU J, QI H B, FANG X J, et al. Quasi-real-time simulation of rotating drum using discrete element method with parallel GPU computing [J]. Particuology, 2011, 9(4): 446-450.

[47] XIONG Q G, LI B, ZHOU G Z, et al. Large-scale DNS of gas-solid flows on Mole-8.5 [J]. Chemical Engineering Science, 2012, 71: 422-430.

[48] XIONG Q G, LI B, XU J. GPU-accelerated adaptive particle splitting and merging in SPH [J]. Computer Physics Communications, 2013, 184(7): 1701-1707.

[49] KRUGGEL-EMDEN H, RICKELT S, WIRTZ S, et al. A study on the validity of the multi-sphere Discrete Element Method [J]. Powder Technology, 2008, 188(2): 153-165.

[50] 戚华彪. 基于GPU的离散模拟在颗粒流动与混合机理研究中的应用[D]. 北京: 中国科学院过程工程研究所, 2014. QI H B. Application of GPU-based discrete simulation to the study of flow and mixing mechanisms of granular materials[D]. Beijing: University of Chinese Academy of Sciences, 2014.

[51] XU J, REN Y, GE W, et al. Mole-MD V1.0[CP]. 2010SRBJ0465, Chinese Software register, 2010.

[52] XU J, QI H B, GE W, et al. DEMMS V2.0[CP]. 2013SRBJ0125, Chinese Software register, 2013.

[53] XU J, QI H B, GE W, et al. DEMMS V3.0[CP]. 2014SRBJ0786, Chinese Software register, 2014.

[54] XU J, WANG X W, HE X F, et al. Application of the Mole-8.5 supercomputer: probing the whole influenza virion at the atomic level [J]. Chinese Science Bulletin, 2011, 56(20): 2114-2118.

[55] REN X X, XU J, QI H B, et al. GPU-based discrete element simulation on a tote blender for performance improvement [J]. Powder Technology, 2013, 239: 348-357.

[56] YUAN F-W, TUAN H-Y. Supercritical fluid-solid growth of single-crystalline silicon nanowires: an example of metal-free growth in an organic solvent [J]. Crystal Growth & Design, 2010, 10(11): 4741-4745.

[57] GUO Y, CURTIS J S. Discrete element method simulations for complex granular flows [J]. Annual Review of Fluid Mechanics, 2015, 47(1): 21-46.

[58] LACEY P M C. Developments in the theory of particle mixing [J]. Journal of Applied Chemistry, 1954, 4(5): 257-268.

[59] LEVENSPIEL O. Chemical Reaction Engineering[M]. New York: Wiley, 1998.

[60] VARGAS-ESCOBAR W L. Discrete Modeling of Heat Conduction in Granular Media[M]. Pittsburgh: University of Pittsburgh, 2002.

[61] WANG L M, ZHOU G Z, WANG X W, et al. Direct numerical simulation of particle-fluid systems by combining time-driven hard-sphere model and lattice Boltzmann method [J]. Particuology, 2010, 8(4): 379-382.

[62] XIONG Q G, LI B, CHEN F G, et al. Direct numerical simulation of sub-grid structures in gas-solid flow—GPU implementation of macro-scale pseudo-particle modeling [J]. Chemical Engineering Science, 2010, 65(19): 5356-5365.

[63] LADD A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation(Ⅰ): Theoretical foundation [J]. Journal of Fluid Mechanics, 1994, 271: 285-309.

[64] 狄升斌. 基于浸入边界法的复杂流动多尺度模拟[D]. 北京：中国科学院大学, 2015. DI S B. Multi-scale modeling and numerical simulation of complex flows based on immersed boundary method[D]. Beijing: University of Chinese Academy of Sciences, 2015.

[65] DEEN N G, KRIEBITZSCH S H L, VAN DER HOEF M A, et al. Direct numerical simulation of flow and heat transfer in dense fluid–particle systems [J]. Chemical Engineering Science, 2012, 81: 329-344.

[66] MA J S, GE W, WANG X W, et al. High-resolution simulation of gas-solid suspension using macro-scale particle methods [J]. Chemical Engineering Science, 2006, 61(21): 7096-7106.

[67] MA J S, GE W, XIONG Q G, et al. Direct numerical simulation of particle clustering in gas-solid flow with a macro-scale particle method [J]. Chemical Engineering Science, 2009, 64(1): 43-51.

[68] PESKIN C S. Flow patterns around heart valves: a numerical method [J]. Journal of Computational Physics, 1972, 10(2): 252-271.

[69] SMAGORINSKY J. General circulation experiments with the primitive equations [J]. Monthly Weather Review, 1963, 91(3): 99-164.

[70] GIDASPOW D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Description[M]. New York: Academic Press, 1994.

[71] ANDERSON T B, JACKSON R. Fluid mechanical description of fluidized beds. Equations of motion [J]. Industrial & Engineering Chemistry Fundamentals, 1967, 6(4): 527-539.

[72] XU M, CHEN F G, LIU X H, et al. Discrete particle simulation of gas-solid two-phase flows with multi-scale CPU-GPU hybrid computation [J]. Chemical Engineering Journal, 2012, 207: 746-757.

[73] XU M, GE W, LI J H. A discrete particle model for particle-fluid flow with considerations of sub-grid structures [J]. Chemical Engineering Science, 2007, 62(8): 2302-2308.

[74] XU B H, YU A B. Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics [J]. Chemical Engineering Science, 1997, 52(16): 2785-2809.

[75] SYAMLAL M, PANNALA S. Multiphase Continuum Formulation for Gas-Solids Reacting Flows[M]. Hershey, New York: Engineering Science Reference, 2011.

[76] KUNII D, LEVENSPIEL O. Fluidization Engineering[M]. 2nd ed. Stoneham, MA (United States): Butterworth Publishers, 1991.

[77] LIU X H, GUO L, XIA Z J, et al. Harnessing the power of virtual reality [J]. Chemical Engineering Progress, 2012, (7): 28-32.

[78] XU J, LI X X, HOU C F, et al. Engineering molecular dynamics simulation in chemical engineering [J]. Chemical Engineering Science, 2015, 121: 200-216.

[79] CHEN W C, GAO Y. The effect of reducing coal slurry particle size on operation of multi-nozzle oppositely placed coal-water slurry gasification system [J]. Chemical Fertilizer Industry, 2015, 42(2): 36-38.

[80] SAKAI M, KOSHIZUKA S. Large-scale discrete element modeling in pneumatic conveying [J]. Chemical Engineering Science, 2009, 64(3): 533-539.

[81] SHAW D E, DENEROFF M M, DROR R O, et al. Anton, a special-purpose machine for molecular dynamics simulation [J]. SIGARCH Comput. Archit. News, 2007, 35(2): 1-12.

[82] SHAW D E, GROSSMAN J P, BANK J A, et al. Anton 2: raising the bar for performance and programmability in a special-purpose molecular dynamics supercomputer[C]//Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (SC14). Piscataway, NJ, USA: IEEE Press, 2014: 41-53

Discrete simulation based on EMMS paradigm and its applications in chemical engineering

XU Ji, LU Liqiang, GE Wei, LI Jinghai
(State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China)

Abstract:Chemical engineering systems typically involve three levels of chemistry, chemical engineering and process system engineering. Each level consists of micro-, meso- and macro-scales, such as the particle, particle cluster and reactor scales in the chemical engineering level. The evolution of the micro-scale elements is naturally described by discrete simulation. However, due to the large number of elements existing in these systems, engineering simulations are mostly based on continuum methods which describe their statistically averaged behaviors and overlook the effects of meso-scale structures, leading to low accuracy and predictivity. This review will explain how this problem can be tackled in a systematic approach that keeps the structural consistency of the problem, physical model, software and hardware, and will demonstrate how discrete simulations with high accuracy, capability and efficiency can be carried out for engineering systems, such as complex molecules, granular flow, and gas-solid fluidization. Realization of virtual process engineering (VPE) is prospected finally.

Key words:discrete simulation; EMMS paradigm; multiphase flow; multiscale; particle; virtual process engineering

Corresponding author:Prof. GE Wei, wge@ipe.ac.cn

中图分类号：TQ 018

文献标志码：A

文章编号：0438—1157（2016）01—0014—13

DOI：10.11949/j.issn.0438-1157.20151468