“以生为本”的课堂如何引导学生掌握数学学习方法
2016-03-19浙江宁波市鄞州区宋诏桥小学315100侯燕妍
浙江宁波市鄞州区宋诏桥小学(315100)侯燕妍
“以生为本”的课堂如何引导学生掌握数学学习方法
浙江宁波市鄞州区宋诏桥小学(315100)侯燕妍
[摘要]“以生为本”的数学教学,重视数学思想方法的渗透和学生学习方法的指导。以“鸡兔同笼”一课教学为例,从教材、前测等方面分析本课学生的学习方法和教学的突破点,旨在使学生获得良好的学习方法,真正理解所学知识。
[关键词]鸡兔同笼学习方法数学教学以生为本
《数学课程标准》对学生的要求由原来的“双基”转变成现在的“四基”,与之前相比增加了基本活动经验和基本思想两方面的内容。本校数学组实施“以生为本”的课堂教学模式,在不断的尝试过程中,笔者发现以往的数学课堂忽略了对学生学习方法的指导。因此,随着课程改革的深入实施,我们学校十分重视教师在数学教学中对数学思想方法的渗透和学生学习方法的指导。下面,笔者以“鸡兔同笼”一课教学为例,与大家探讨数学课堂上对学生学习方法的指导。
一、分析教材,明确解决“鸡兔同笼”问题的学习方法
“鸡兔同笼”问题原来安排在实验教材的六年级,但是该内容对于六年级学生来说挑战性不足,且方程解法对其他方法的学习也造成了一定的干扰。修订后的教材将“鸡兔同笼”问题安排在四年级,删去了方程解法,更加突出了列表法和算术法的作用。教材这样编排,旨让学生经历“假设——比较——调整——验证”的过程,使他们体会到解决问题的一种重要策略——假设法。
在解决“鸡兔同笼”问题的方法中,猜测是探究、解决此类问题的基础,其中列表法有助于通过有序思考找到问题的答案,而假设法则有利于培养学生的逻辑推理能力,且是解决此类问题的一般方法。但细细分析,无论是列表法假设还是算术法假设,对于四年级学生来说理解都是比较抽象的,如果加以图辅助,对学生来说会更加容易理解。分析教材和学生的实际情况后,笔者认为:在解决“鸡兔同笼”问题时,引导学生出现画图的方法,这样更有利于学生沟通各种解题方法之间的联系,从而理解假设法。
基于以上分析,笔者对本课的教学目标有了一定的定位,但在一节体现学生自主学习、合作探究的课上,如何帮助学生达到目标呢?为客观分析学生,笔者对学生进行了前测。
二、通过前测,了解学生运用学习方法的能力
前测就是学习前测,测试的结果可以显示学生学习的当前水平。通过对全班46名学生进行前测,结果发现:错误27人(58.7%),其中21人完全不会做,正确19人(41.3%)。近半数学生能利用已有的知识经验解决这道题,主要的正确解法如下。
1.口算法(2人,占全班人数的4.3%)
这类学生的数感特别强,但如果数据变大,这两位学生并不见得能口算出结果。
2.列表法(包括不完整列表法和完整列表法)
(1)不完整列表法(3人,占全班人数的6.5%)。
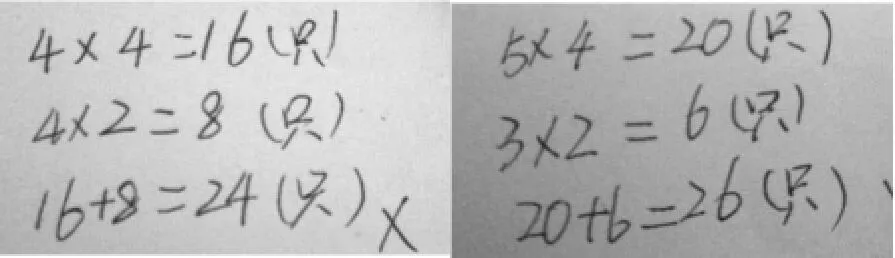
这类学生首先是直观的凑数、计算,这其实是把列表的具体过程呈现出来,暂且把它归纳为不完整列表法。
(2)完整的列表法(3人,占全班人数的6.5%)。
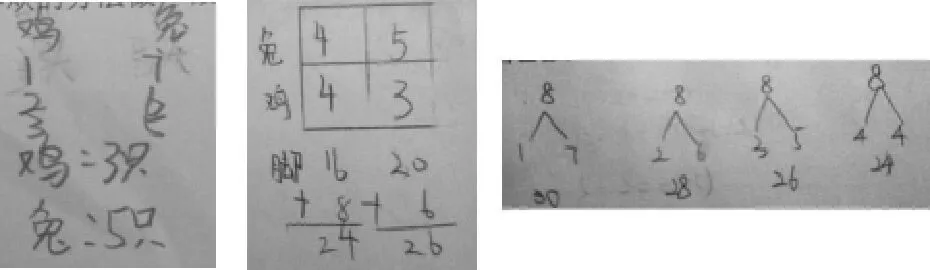
这三名学生的数学思维已经非常严谨了,会用完整的列表法通过不断假设调整,最后得到结论。
3.算术法(11人,占全班人数的23.1%)

这类学生脑中已经有了非常清晰的假设法,但所占的比例不大。
通过前测了解到,解决“鸡兔同笼”问题,有14名(29.6%)学生有较严密的逻辑思维能力。因此,课堂上学生能在独立探究的基础上进行小组合作学习,但是如何激活另外32名学生原有的学习方法,使他们能正确解决问题,是本节课教学首要解决的问题。
三、展开教学,形成学习方法
1.回顾——激活已有的学习方法
学生的学习是建立在已有的生活经验和认知水平基础上的,所以课堂上如何激活学生已有的认知很重要。因此,本课伊始,安排学生回顾以往的学习过程,激活他们已有的学习方法,为后续的解决问题做好铺垫。
教学片断:
师:课前大家已经完成了阅读资料(略),那你知道解决问题的方法有哪些吗?
生:列算式、画图、列表……
师(小结):看来,解决问题的方法除了我们熟悉的算术法之外,还有画图、列表、枚举等。
……
本节课一些解决问题的方法在学生之前学习中都已经出现过,但多数学生没有想到可以用这些方法来解决。因此,课前设计让学生回顾已学过的知识,旨在唤起学生已有的知识经验,为今天这节课解决问题提供参照。
前测和教材中都没有出现画图法,但画图法在解决“鸡兔同笼”问题中却有着不可取代的作用,既能很好地沟通列表法和算术法之间的联系,又能帮助学生形象地理解解决问题的具体过程,同时还是假设法的本源所在。因此,笔者在阅读材料中加入了画图法,旨在指导不会做的学生理清思路,尝试解决问题。
2.放手——应用学习方法解决问题
学生思维火花的碰撞,一定是在充分思考后发生的。因此,课堂教学中,教师应给学生提供充分思考和交流的时间与空间,这样学生才会还课堂以精彩。因此,在本课设计中,笔者放手让学生自由思考,先应用已有的学习方法解决问题,再讨论、梳理获得的方法。
教学片断:
(1)学生独立尝试解决问题。
(2)组内共学。
①每位成员介绍自己的方法。
②其他成员认真倾听,及时补充。
③组长整理、汇总方法,并在共学单上做好记录。
……
通过学习方法的回顾,学生在独立尝试环节就出现了多样化的方法。从学生的方法中可以看出,画图和列表这两种解决问题的方法对学生的指导意义最大了。
组内共学是数学课程改革课堂教学的重点所在,但共学的内容必须有价值,有可探讨性。“鸡兔同笼”问题无论是在方法指导前还是在方法指导后,学生间的个体差异都是客观存在的。此外,学生的思考方式也存在很大的差异,一个合作组内一定会有学生有不同的方法。因此,“鸡兔同笼”问题很适合学生进行小组探讨交流,既能帮助有困难的学生理解解题步骤,又能通过思维碰撞,使学生初步感知解决问题的策略。
3.推进——形成新的数学学习方法
学习方法的形成,不是多种方法展示后就能形成的,而是在不断对比、沟通中逐步形成的。因此,在本课教学时,笔者安排全班展学活动,并引导学生分析、对比多种方法,使学生形成解决问题的策略。
教学片断:
(1)小组展示作品。
画图法:不管是全部假设成鸡还是全部假设成兔子,都是和26只比较后2只2只增加或减少的。
列表法:可以从鸡8只、兔0只或鸡0只、兔8只进行极端假设,也可以取中间数假设,然后和26比较,进行调整,直到正确为止。
算术法:结合图解释算术假设的过程。
(2)方法沟通,总结出假设法。
师:这些方法都有什么相同之处?
生:不管哪种方法,要不假设全部是鸡,要不假设全部是兔,然后和题目中的26比较,接着一个一个调整,最后得到答案。
……
萧伯纳说过:“你有一种思想,我有一种思想,我们彼此交换,每人可拥有两种思想。”在全班展学环节,可安排其他组进行补充和提问,这样学生会碰撞出更多智慧的火花。如课堂上,其他组学生对于取中间数假设的同学进行提问:“你后来是假设兔子5只、鸡3只,那为什么不是兔子3只、鸡5只这样往上面调整?”通过争论,学生理解脚的总只数和题中的26比较后,多了要减少脚只数多的兔子,少了就要增加脚只数多的兔子。
4.变通——提升数学学习方法
数学教学的目的不是为了解决一道问题,而是希望学生掌握解决一类问题的方法。将“鸡兔同笼”问题进行变通,使学生感受到生活中存在很多此类问题,在解决此类问题中不断形成数学思想方法并得到提升。
教学片断:
(1)环保卫士小分队6人参加植树活动。男生每人栽了3棵树,女生每人栽了2棵树,一共栽了16棵树。男、女生各有几人?(选择正确画法)
(2)盒子里有大、小两种钢珠共30颗,共重222g。已知大钢珠每颗11g,小钢珠每颗7g。盒中大、小钢珠各有多少颗?(选择合适的列表法)
(3)全班一共有38人,共租了8条船,每条船都坐满了。大、小船各租了几条?(独立完成)
(4)有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?(独立完成)
师(总结):解决问题有什么样的策略?
……
本课选用的练习素材形式多样,旨在将这些问题进行变通,使学生掌握一类问题的解决方法。从练习结果中可以看出,解决这类问题,画图、列表和算术这三种方法学生都有用到,但用算术法解决问题的学生占多数,说明学生已经真正理解了这类问题的逻辑推理过程。全课总结环节看似简单,却渗透了深刻的数学思想方法。通过回顾全课,使学生形成了自己的数学学习方法,最后总结、提升为解决一类问题的方法。
通过本节课的设计,旨在从关注知识点的教学到学习方法的指导,如从课始的方法回顾到最后的方法总结,让学生形成一个完整的数学思考模式:当遇到不会做的问题时,我们可以通过回顾原来学过的方法,一个个进行尝试,最后形成新的数学思想方法。这就是教给学生数学学习的方法,即所谓的“授之以渔”。
(责编蓝天)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)01-025
