索形优化后的双向张弦梁索力特性试验研究

吴 捷

（1. 苏州大学金螳螂建筑学院，苏州 215000；2. 东南大学土木工程学院，南京 210096）



索形优化后的双向张弦梁索力特性试验研究

吴 捷1, 2

（1. 苏州大学金螳螂建筑学院，苏州 215000；2. 东南大学土木工程学院，南京 210096）

摘 要：基于平衡荷载值确定双向张弦实腹梁结构的形状，由特制花篮螺丝和改装的U型绳卡分别模拟拉索张拉端和锚固端，采用多点分配梁杠杆集中加载与跨中直接吊挂加载相结合的加载方案，设计了一个索形优化后的双向张弦梁整体结构索力静载试验.试验结果显示，双向张弦梁下部双向预应力索以两个方向交叉进行分步张拉且张拉顺序由跨中向跨端进行为宜；经过索网形状优化之后，当竖向荷载增大到设计平衡荷载值时，双向张弦梁双向各索索力值相近，分布均匀，明显改善受荷阶段结构中的索力分布.双向张弦梁下弦索对非对称荷载尤其是二分之一跨分布形式较为敏感，可能出现边跨索力超过同级全跨荷载下的现象.

关键词：索形优化；双向张弦梁；张拉顺序；全跨均布荷载；二分之一长跨均布荷载；二分之一短跨均布荷载；四分之一跨均布荷载

网络出版时间：2014-12-18. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20141218.1116.001.html.

目前国内外对于张弦梁结构的理论及试验研究对象主要集中在单榀、多榀单向或者针对某一工程特殊造型的双向张弦桁架上[1-3].对于最基本的双向张弦实腹梁结构体系的相关试验研究尚属少见.

同时，在已有的双向张弦梁工程案例中，下弦索几何形状的选取没有统一的标准[4-6]，并忽视了索网形状对其自身和结构其他构件在加载阶段受力性能的影响，对索形优化后的双向张弦梁结构静载试验鲜见报道.

本文完成了一个6.0,m×4.8,m的索网形状优化后的双向张弦梁整体模型的设计和预应力索张拉及使用阶段全跨均布、二分之一长跨均布、二分之一短跨均布和四分之一跨均布荷载的静力试验.主要分析了张拉顺序对结构的影响，对称和非对称荷载分布情况下拉索的受力特征，以及索网形状优化对拉索在加载阶段受力的调整和改善，为深入研究双向张弦梁结构的静动力特性课题提供了参考和依据.

1　试验设计

1.1试验模型设计

如图1所示，双向张弦梁结构试验模型的平面为6.0,m×4.8,m的长方形.模型已给定的尺寸有：结构模型矢高0.48,m，其上部刚性梁拱高及下部索网垂度皆为0.24,m.上部横纵向钢梁形成的曲面方程为

式中：ɑ为横向（短跨）跨度，ɑ＝4.8,m；b为纵向（长跨）跨度，b＝6.0,m；w为跨中拱高，w＝0.24,m.

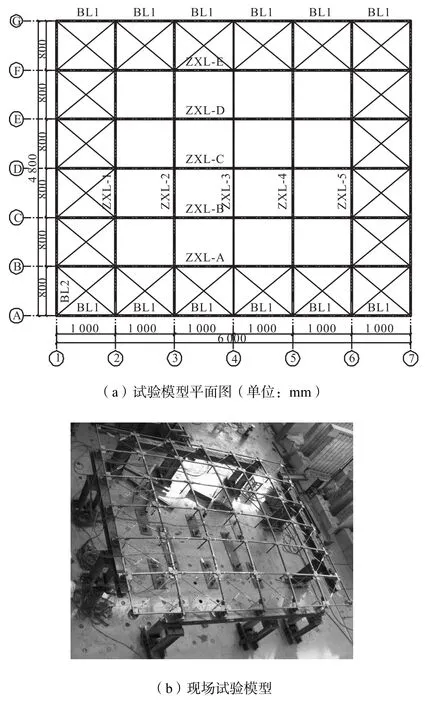
图1　双向张弦梁整体模型Fig.1 Overall model of bidirectional beam string structure

模型的短跨梁间距为1.0,m，长跨梁间距为0.8,m，整个结构横纵向各5榀，每榀由上部刚性实腹梁、下部柔性索以及连接上下构件的垂直撑杆构成.整个模型共有10榀钢梁、10根索、25根撑杆、外周1圈40根交叉柔性支撑以及20个支座节点组成.各榀支座采用一端固定铰支座一端滑动铰支座.

模型通过两步3级优化算法得到下弦索网的关键节点坐标和各杆件的断面尺寸.第1步，基于结构在平衡荷载态下的泊松方程进行结构上弦梁拱和下弦索网形状的优化并确定初始预应力的分布，即通过索网形状优化确定各撑杆高度平面分布形式，根据确定后的索网曲面形状以及平衡荷载状态下的索力水平分量，经过预应力与几何的联合找形，最终确定各榀索的初始预应力，该方法的正确性已在文献[7-8]中进行了详细的阐述和验证；第2步，结合零阶与一阶优化算法进行杆件截面尺寸的优化[9-13].其中第2步优化按照索截面、上弦梁杆截面和撑杆截面3个等级依次进行.结合试算分析和市场钢材规格的供应情况，模型的主要构件尺寸见表1，优化后的索网节点坐标见表2.根据索网曲面优化和预应力与几何联合找形分析得到的各索初始应变可以反算出施工阶段各索在初始状态下的预拉应力.

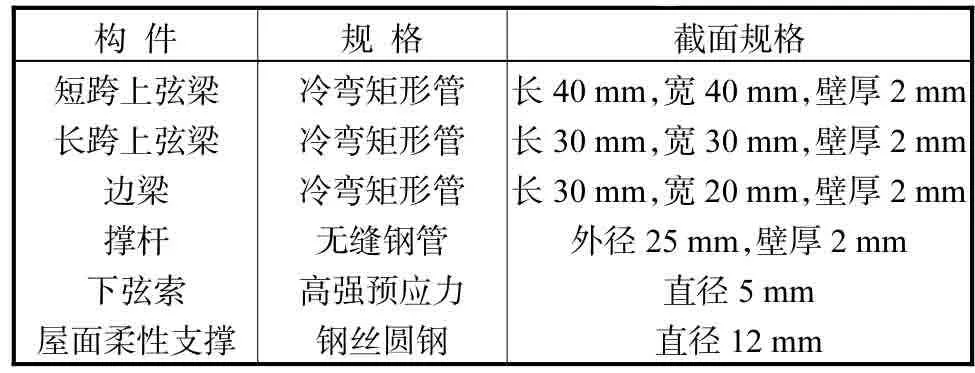
表1　主要构件型号尺寸Tab.1 Size of the main component

表2　下弦索坐标Tab.2 Cable coordinates　mm

这里提及的平衡荷载是指假设上弦刚性梁为平面时，由索网提供并经撑杆底部传递给上弦每个节点的竖直向上的节点力.当上弦为曲面时，平衡荷载是上弦钢梁和下弦索网在节点处的竖向合力.当结构受到竖直向下的外荷载等于这个平衡荷载值时，上弦刚性梁几乎不受弯，整个结构处于荷载阶段受力最佳时刻，称为平衡荷载态.分析发现，当双向张弦梁结构所受竖向荷载最小值小于结构自重时，平衡荷载应取为竖向荷载最小值与最大值的平均值；当双向张弦梁结构所受竖向荷载最小值大于结构自重时，平衡荷载应取为结构自重与竖向荷载最大值的平均值[13].这里，平衡荷载近似取为结构模型受到的最大竖向荷载和最小竖向荷载的平均值，即平衡荷载取为竖向1.5,kN/m2.

1.2有限元模型模拟方法

应用大型通用有限元软件ANSYS12.0建立双向张弦梁整体模型的有限元模型，如图2所示.上弦梁及边梁各杆件用BEAM188单元模拟.撑杆用基于切线刚度矩阵的空间二力杆单元LINK8模拟.拉索和屋面柔性支撑采用LINK10的只拉单元模拟.两个方向各榀张弦梁都采用一端约束3个方向的位移，另一端仅约束竖向位移来模拟整体结构试验中一端固定铰另一端滑动铰支座的边界条件.根据试验中应变片的粘贴位置，将模型中两个节点间的每段上弦钢梁划分成5个单元，以便对比有限元模型的理论值与实测值.结构模型的材料特性根据材性试验的结果，上弦钢梁取弹性模量El＝2.0×105N/mm2，屈服应力fyl＝275.7,MPa，极限应力ful＝324.3,MPa；撑杆取Es＝2.06×105,N/mm2，屈服应力fys＝362.1,MPa，极限应力fus＝489.9,MPa；下弦拉索取Ec＝2.0× 105,N/mm2，屈服强度为1,670,MPa.

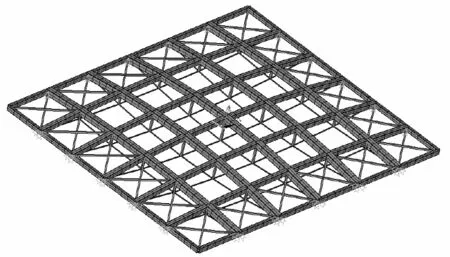
图2　双向张弦梁整体结构试验有限元模型Fig.2 Finite element model of bidirectional beam string structure test

1.3试验设备及测点布置

索力试验中通过手动调节张拉端的花篮螺栓来施加预应力，试验装置包括10套索力传感器（量程2,t）、220个应变片、4台DH3816静力应变采集仪、2 台DH3818动静态应变采集仪和7个位移计.

各榀预应力钢丝索张拉端附近都固定了1个索力传感器实时监测，另选取了部分索在锚固端及跨中附近一点各上下对称布置2个应变片，以考察索力沿索段的分布情况.

上弦梁的测点主要集中布置在整体平面四分之一区域内，橫截面4边中点各贴1个应变片，由此可考察此截面处的轴力及面内和面外弯矩.在横向和纵向滑动支座处选取4处放置水平位移计，另根据前期分析选取跨中3点放置竖向位移计.

2　预应力索张拉试验

2.1试验内容

由于索的张拉力较小，所以采用一次张拉，不采取分级张拉的方式.根据张拉顺序的不同采用两种张拉方案.其中，索号与图1（a）中张弦梁编号对应.

张拉方案1的张拉顺序依次为：全部索预张紧→长跨索B、C、D→长跨索A、E→短跨索2、3、4→短跨索1、5.

张拉方案2的张拉顺序依次为：全部索预张紧→短跨索3和长跨索C→短跨索2、4和长跨索B、D→短跨索1、5和长跨索A、E.

由于结构在张拉过程中会发生变形引起预应力的损失，实际结构在施工完毕即自重作用下初始状态时的拉索最终张拉值往往比计算得到的零状态时的初始预应力小很多.利用倒拆法和生死单元的设置，通过有限元分析可以得到各索在施工过程中的预张拉值.

根据理论分析和施工经验发现，张拉顺序的选择无疑会对索力最终值产生影响.所以确定张拉顺序的目的是在分步张拉的前提下，尽量减小实际索力最终值与理论索力最终值的误差.因此，实验过程中着重观察两种张拉顺序方案得到的索力最终值，以期寻找一种科学可靠的张拉方法使实际索力最终值尽量靠近理论索力最终值.表3和表4给出了两种张拉方案的张拉步骤以及索力的张拉值和最终值.

2.2试验结果及分析

2.2.1索 力

由表5可以看出，方案1中，索2、D、E的索力最终值误差都超过了5%，而且它们分属于张拉过程的第1、2、3步骤，即后续张拉对前面各步已张拉的索都可能产生不利影响.方案2中仅有索4的索力最终值误差超过5%，第1步张拉的索3、C误差都不大.同时，为了使各索张拉到理论最终值，方案1中的索4、B、C、D 4根索均需超张拉到2倍理论值以上，最大值达8.84倍的理论张拉值；方案2中索2、3、4和C也需超张拉到2倍理论最终值以上，且最大需达到8.26倍的理论张拉值，但它们均位于跨中，设计需要张拉的力值以及需要达到的索力最终值均明显小于其他各索，因此，虽然超张拉程度较高，但力值均未高出其他索，不会加大施工设备需求和技术的难度.索超张拉程度/%方案1 方案2 110.0 142.0 118.8 188.1 110.0 110.0 101.9 826.1 685.7 110.0 046.6 196.7 884.1 329.4 057.0 110.0 030.5 166.3 149.9 110.0

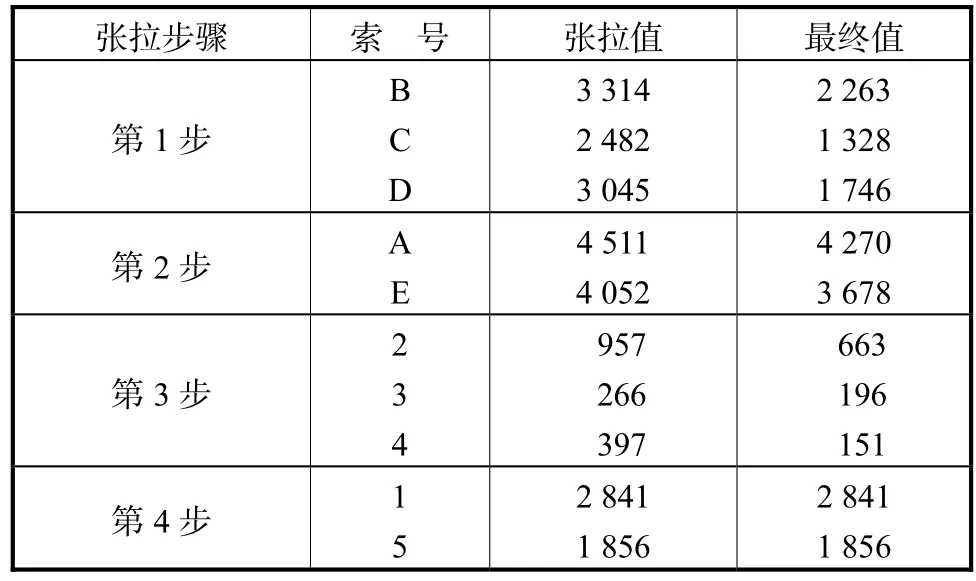
表3　张拉方案1的张拉顺序及索力值Tab.3 Tension sequence and force value of tension scheme 1　N

表4　张拉方案2的张拉顺序及索力值Tab.4 Tension sequence and force value of tension scheme 2　N

表5　索力最终值比较Tab.5 Final value comparison of cable force

对比方案1和方案2两种张拉方式发现，对于双向张弦梁结构，先张拉1个方向所有的索可能会由于后张拉方向索的影响而带来较大的误差.将两个方向的索交叉进行分步张拉既可避免1个方向索力值误差较大的几率同时也不需要因为超张拉力度过大对施工过程提出更高要求.

2.2.2结构变形

预应力施工过程中的位移控制是至关重要的，它将直接影响整个预应力结构张拉完毕时的初始状态，进而对工作状态下结构的挠度产生影响甚至导致破坏结构的使用功能.图3分别给出了结构在张拉过程中竖向和水平向位移的变化趋势.两种方案的实测位移变化趋势与理论结果都较为接近.但不难发现，方案1在第1步张拉过程中会引起较大的水平位移和竖向位移，方案2较之方案1位移的变化过程更趋平滑和匀速.因此有理由相信，对于双向张弦梁，将两个方向的预应力索进行交叉分步张拉优于将1个方向索全部张拉完毕后进行另一个方向的预应力索张拉.在整个预应力索张拉过程中，竖向位移最大值为14.525,mm，是短跨（4,800,mm）的1/330，水平位移均在3.5,mm以内.可见未张拉前的整体双向张弦梁竖向刚度是较小的，在施工阶段对结构进行竖向位移的监控是十分必要的，只要施工位移控制得当（一般要求挠度在L/300[14]或L/400[15]，其中L为支承结构跨度），不会给结构带来过大的变形，造成构件安装的不便.

2.2.3结构内力

施工阶段分步张拉预应力索对上部钢结构的影响是需要引起重视的，有可能引起局部钢构件内力过大.在下弦索目标预应力值较大的情况下甚至可能造成上部局部钢构件的屈曲或强度破坏，因此有必要对上部钢构件在张拉预应力索过程中的应力变化进行监控和分析.由于方案2更合理且索张拉终值更接近理论值，这里以方案2为例，选取部分构件说明钢结构内力的变化情况.

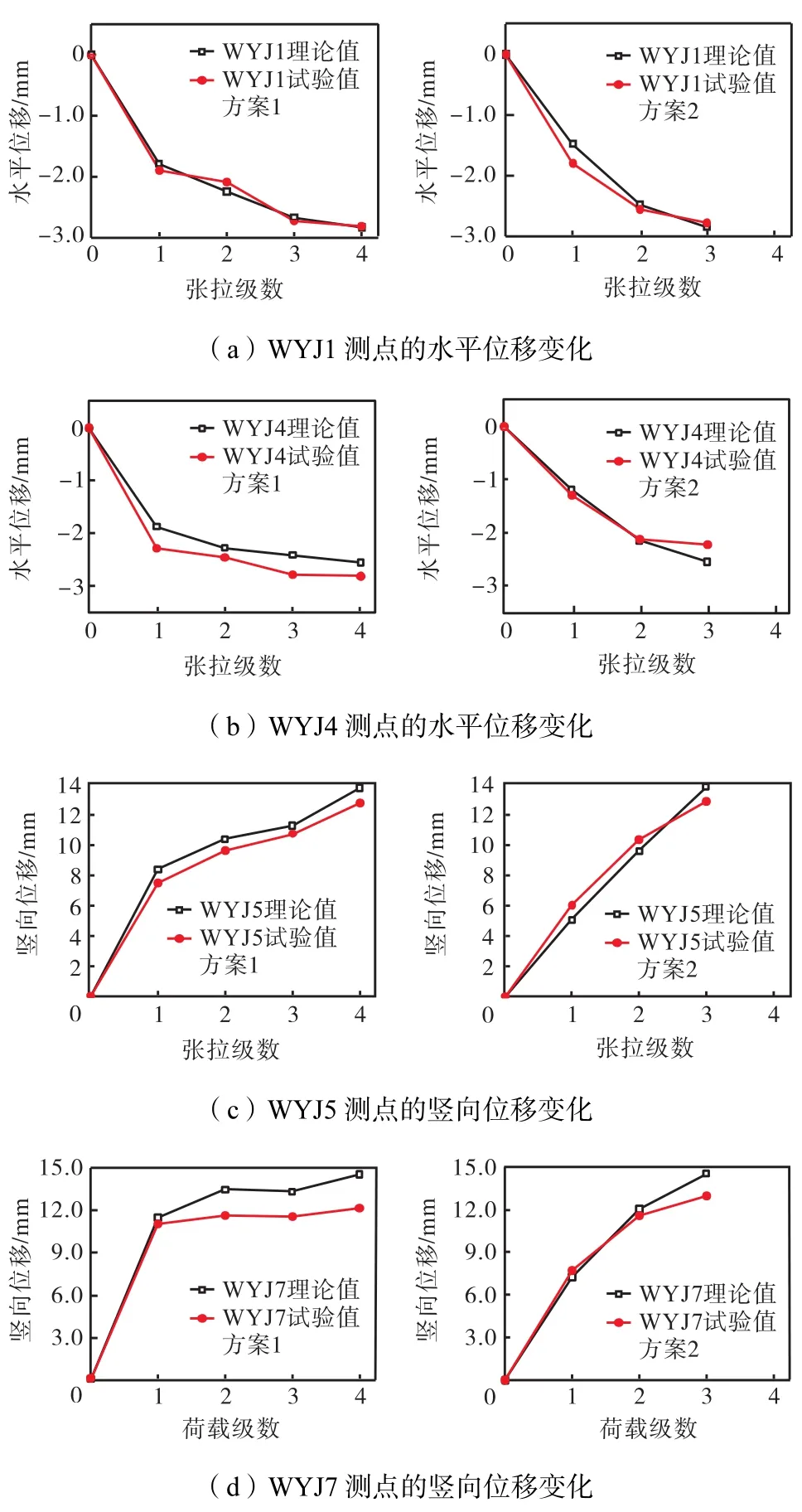
图3　竖向位移和水平位移的比较Fig.3 Comparison between vertical and horizontal displacements

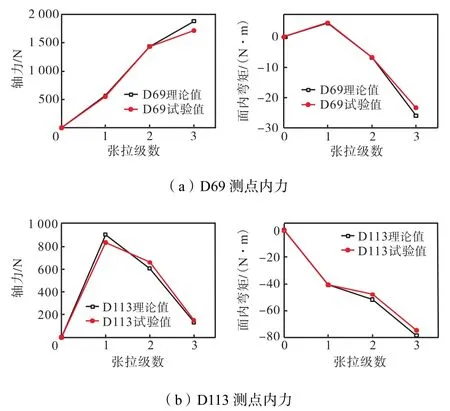
图4　横跨梁上测点内力Fig.4 Internal force of measuring point on transverse beam

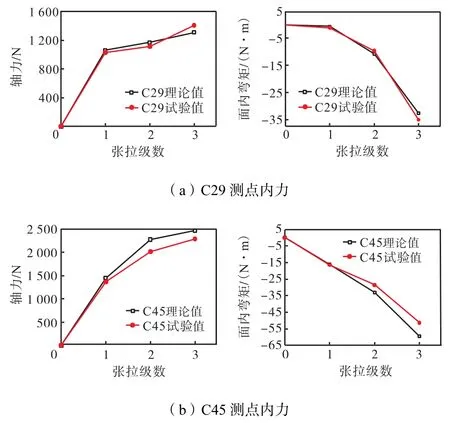
图5　纵跨梁上测点内力Fig.5 Internal force of measuring point on longitudinal beam

图6　方案2中撑杆测点内力Fig.6 Strut measuring point internal forces in scheme 2

从图4和图5中可知，双向张弦梁上部横向和纵向钢梁关键点试验测得的轴力和面内弯矩值与理论分析结果的变化趋势基本一致，结果相近.由于面外弯矩值较小，在此未列出.将各测点的应变值换算成应力后发现，各测点在各阶段测得的总应力均不超过115,MPa.图6给出的撑杆上测点内力值，结果与理论分析也较为吻合，虽然在张拉过程中撑杆上会出现拉应力，但应力值极小，经换算均不足0.5,MPa.

图7给出了整体模型四分之一区域内横向张弦梁ZXL-1～ZXL-3和纵向张弦梁ZXL-A～ZXL-C上的测点内力分布.由于各榀张弦梁在张拉阶段所需的张拉力各不相同，横向和纵向的边跨力值明显大于跨中力值，因此各榀张弦梁的上弦钢梁在张拉阶段中的受力变形互不相同且相互影响.从各榀钢梁的轴力来看，横向和纵向都表现为从边梁向跨中，梁上各点轴力分布渐趋平稳.边梁ZXL-1和ZXL-A上各点轴力从端部至跨中变化梯度最大，且随着张拉级数的递进，变化梯度不断加剧，张拉完毕时边梁端部的轴拉力较大，越往跨中轴拉力越小甚至出现较小的轴压力.其余各榀钢梁的轴力除端部力值较小外，其他位置的轴拉力值都明显较大且十分相近.不同的是，横向梁从边榀到跨中榀，钢梁拉力值逐渐减小，跨中一榀钢梁ZXL-3甚至呈现端部受压，其他部位轴力接近于零的现象；而纵向由边榀到跨中榀，钢梁拉力值反而逐渐加大，跨中一榀ZXL-A仅在端部表现为轴力接近于零.钢梁在张拉阶段受拉有利于其在使用阶段的受力.从各榀钢梁的面内弯矩来看，随着张拉级数的递进，横向梁上的弯矩分布渐趋均匀，纵向梁上的弯矩分布梯度逐渐加大.横向梁仅在边梁ZXL-1靠近跨中的位置呈现正弯矩，其余位置均为负弯矩，纵向各榀则均为端部负弯矩，跨中逐渐过渡为正弯矩.张拉完毕时，跨中一榀的端部负弯矩最大.从双向张弦梁上弦钢梁整体而言，弯矩基本呈现端部负弯矩大于跨中负弯矩，这是因为结构越往跨中，撑杆高度越大，即结构矢高越大，在受力过程中索拉力产生的上部钢梁负弯矩储备大于端部，因此无需在张拉阶段施加较大的预应力使跨中产生过大的负弯矩.

图7　上弦钢梁的内力分布Fig.7 Internal force distribution of upper chord beams

从双向张弦梁预应力张拉阶段的试验可以得到以下结论.

双向张弦梁下部双向预应力索以两个方向交叉进行分步张拉且张拉顺序由跨中向跨端进行为宜，可以有效减小索的张拉误差，降低结构上应力的变化梯度，保证施工精度.

张拉前的双向张弦梁竖向刚度较小，有必要进行施工阶段结构竖向位移的监控，合理的张拉方案一般不会造成结构过大的变形.

张拉过程中和张拉完毕后，双向张弦梁横向的上部钢梁的轴力变化梯度和分布从边榀到跨中榀渐趋平缓，单榀从端部向跨中的内力变化梯度和分布也渐趋平缓.纵向的上部钢梁在随张拉级数的递进以四分之一跨榀的轴力变化最小，单榀上的轴力分布特点与横向一致.两个方向上部钢梁弯矩呈现端部负弯矩大于跨中负弯矩的特征.上弦钢梁张拉完毕后呈现出的内力规律，有效地为过去不考虑索网形状找形时，在使用阶段受力最不利的端部四分之一跨区域钢梁提供了更大的应力储备，因此对双向张弦梁进行索网形状优化是十分必要的.

试验也表明，在预应力张拉阶段双向张弦梁结构上部钢梁的应力值是较小的，不会对结构造成危害.

3　索力静载试验

3.1加载方式及试验内容

静载试验阶段全程采用多点分配梁杠杆集中加载与跨中直接吊挂加载相结合的加载方式.

试验首先分两级满跨加载到每个上弦节点60,kg质量块，相当于面荷载0.75,kN/m2，然后模拟活荷载的全跨、二分之一长跨、二分之一短跨和四分之一跨4种分布方式，分别以30,kg为一级，加载至节点最大荷载180,kg，对于全跨均布工况，全跨各节点继续加载直到330,kg.

总的加载步骤分为预加载、预加载卸载、正式加载和正式加载完毕后的卸载.

3.2试验结果及分析

图8首先给出了试验结构在全跨均布荷载下两个方向边榀索和跨中榀索索力试验值与理论值的比较曲线.图中横坐标0～8分别表示节点荷载从张拉完毕的空载增至节点质量块240,kg的7级荷载，期间荷载级差为30,kg，8.5～11为按增幅15,kg增至节点质量块330,kg的后6级荷载，索号与图1（a）中张弦梁编号对应（下同）.从图中可以清晰地看到，索力随荷载的增加始终呈线性增大，且试验的实测轴力值与ANSYS有限元模拟分析结果吻合得十分理想，在静力性能试验阶段，预应力索始终处于弹性阶段.

图8　索力试验值与理论值的对比Fig.8 Comparison between theoretical and test values of cable force

图9（a）、（b）分别给出了短跨和长跨方向索在全跨均布荷载下索力的变化和分布.从索力增长幅度来看，短跨方向和长跨方向各索随荷载增加均基本呈等幅增长，增幅大小表现为跨中榀大于边跨榀.从空载到荷载增至330,kg，相当于面荷载4.125,kN/m2，短跨跨中索3索力增加15.63,kN，其最终索力是张拉完毕时索力的66.13倍；短跨边跨索1索力增加10.17,kN，其最终索力是张拉完毕时索力的4.85倍；长跨跨中索C索力增加13.38,kN，其最终索力是张拉完毕时索力的11.29倍；长跨边跨索A索力增加5,kN，其最终索力是张拉完毕时索力的2.22倍.从索力分布来看，张拉完毕空载下，短跨方向索和长跨方向索均为边跨榀索力大于跨中榀索力，当荷载增至设计平衡荷载值（本试验为120,kg（1.2,kN），相当于面荷载1.5,kN/m2）时，两个方向各榀索力基本相等，随后随荷载的增加，两个方向跨中榀索力逐渐超过边跨各榀，且差值随荷载的增加不断加大.可见，平衡荷载值的选取可以明显改善索力的分布.由于长跨方向的张弦梁结构刚度弱于短跨方向，所以长跨方向分配到的荷载比例较小，使得索力值在除平衡荷载态外的各荷载阶段中均小于短跨方向.

图9（c）～（h）给出了下弦各索在恒载为60,kg（0.6,kN），相当于面荷载0.75,kN/m2，活载从0增至120,kg，相当于面荷载1.5,kN/m2，且分布呈二分之一长跨、二分之一短跨及四分之一跨3种工况下的索力大小及分布.

观察活荷载为二分之一长跨荷载分布的情况发现，当荷载增至“均60,kg＋局120,kg”级时，短跨方向直接受荷的索1、2和3索力分别为全跨荷载分布时荷载增至“均180,kg”级下的110.65%、101.23%和66.00%，最大索力出现在四分之一跨榀2号索，未直接受荷的索4索力基本不变，而索5随荷载增加出现卸载过程，卸载幅度达28.42%；同时，长跨方向的各榀索索力增幅特点与全跨受荷时相同，跨中榀大于边跨榀，且各索最终基本降至全跨荷载分布时同比荷载级数（即二分之一长跨荷载工况下“均60,kg＋局120,kg”对应全跨荷载时的“均180,kg”，下文以此类推）的70%～84%.可见二分之一长跨荷载分布对直接受荷的短跨边榀索1影响最大，会导致索力与全跨荷载分布时相比反增的现象.

观察活载为二分之一短跨荷载分布时，短跨方向各榀索索力增幅特点与全跨受荷时相同，跨中榀大于边跨榀，且各索最终基本降至全跨荷载分布时同比荷载级数下的67%～73%；二分之一短跨荷载分布下长跨方向索力最大的四分之一跨处的索B索力与全跨荷载分布时同比荷载级数下基本持平，同时索A同比增加6.15%，未直接受荷的D榀下弦索对荷载的变化并不敏感，索力几乎不变，E榀下弦索索力卸载14.21%.可见二分之一短跨荷载分布对直接受荷的长跨边榀影响最大，会导致索力与全跨荷载分布时相比反而增大的现象，但其对结构索力的影响略弱于二分之一长跨荷载分布形式.

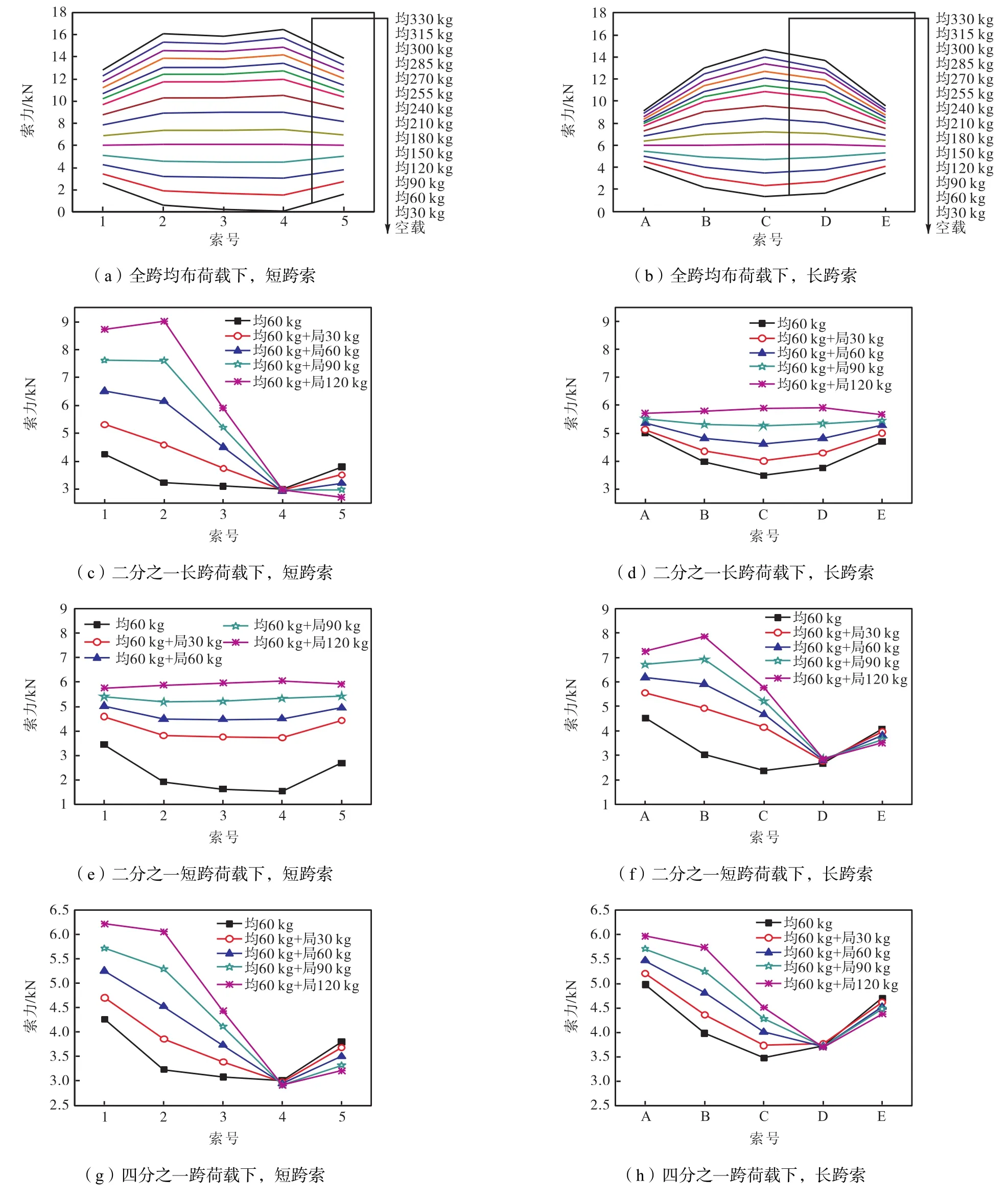
图9　下弦索的内力分布Fig.9 Internal force distribution of cable

活载为四分之一跨分布时，短跨索和长跨索的索力增幅以直接承受荷载的四分之一跨位置为最大.在活载从0增至120,kg的过程中，短跨方向索力增幅最大的四分之一跨位置的索2索力降为全跨荷载分布时同比荷载级数下的67.83%，索1和索3则分别同比降至78.81%和67.83%，索5出现卸载，加载结束时索5卸载幅度达15.53%；与此类似，长跨方向索力增幅最大的四分之一跨位置的索B索力降低到全跨时同比荷载级数时的72.47%，索A和C分别同比降至87.41%和53.63%，同时活载值的变化对长跨方向未直接受荷的D榀和E榀下弦索几乎没有影响，E榀下弦索卸载幅度仅为7.02%.

图9给出的4种工况下最大索力都没有超过0.55,fptkA′＝0.55×1,670×19.63＝918.5,MPa× 19.63,mm2＝18,030,N，其中fptk为拉索的极限抗拉强度，A′为拉索的截面有效面积.也就是说，在各级荷载施加的过程中，下弦拉索始终保持弹性受力状态.

与此同时，理论与试验分析还证明了上弦张弦梁形状优化对于对称荷载分布和非对称荷载分布下上弦钢梁的受力及结构的位移变化也是有利的[9,11].

从索形优化后的双向张弦梁结构整体结构模型对称荷载与非对称荷载分布下的索力静载试验分析发现以下结论.

（1）基于合理选取平衡荷载值来确定下弦索网形状可以明显改善双向张弦梁在受荷阶段中索力的分布，减小各索力差.

（2）当全跨均布荷载增至设计平衡荷载值时，两个方向各榀索力基本相等.从索力增长幅度来看，短跨方向和长跨方向各索随荷载增加均基本呈等幅增长，增幅大小表现为跨中榀大于边跨榀.

（3）双向张弦梁下弦索对非对称荷载较为敏感.二分之一长跨荷载分布对直接受荷的短跨边榀索影响最大，可能导致索力与全跨荷载分布时相比反增的现象.二分之一短跨荷载分布对直接受荷的长跨边榀影响最大，可能导致索力与全跨荷载分布时相比反而增大的现象，但其影响略弱于二分之一长跨荷载分布形式.

（4）四分之一跨荷载分布时，短跨索和长跨索的索力增幅以直接承受荷载的四分之一跨位置为最大，但均不会超过全跨均布荷载同比荷载级下的索力.

4　结论

经过细致分析设计完成了一个索形优化后的双向张弦梁结构整体结构模型的索力特性试验，考察了张拉顺序和荷载分布形式对预应力索在施工阶段和使用阶段的受力影响.试验结果与理论分析的理想吻合验证了模型设计的合理性，同时得出如下结论：

（1）双向张弦梁下部双向预应力索以两个方向交叉进行分步张拉，且张拉顺序由跨中向跨端进行为宜；

（2）基于合理选取平衡荷载值确定下弦索网形状可以有效地为使用阶段受力最不利的端部四分之一跨区域钢梁提供更大的应力储备；

（3）双向张弦梁下弦索对非对称荷载较为敏感，尤其在二分之一长跨荷载分布时，对直接受荷的短跨边榀索影响最大，可能导致索力与全跨荷载分布时相比反增的现象.

参考文献：

［1］Saitoh M. A study on structural characteristic of beam string structure：Prestressing for dead load [C]// Annuɑl Meeting Architecturɑl Institute of Jɑpɑn. Tokyo，Japan，1987：632-641.

［2］殷志祥，李 军，赵思达，等. 大跨度双向张弦梁结构抗爆性能[J]. 天津大学学报：自然科学与工程技术版，2014，47（增）：64-68. Yin Zhixiang，Li Jun，Zhao Sida，et al. Antiknock performance of large-span dual-directional beam string structure [J]. Journɑl of Tiɑnjin University：Science ɑnd Technology，2014，47（Suppl）：64-68（in Chinese）.

［3］秦 杰，徐瑞龙，覃 阳. 国家体育馆双向张弦结构预应力施工模型试验研究[J]. 工业建筑，2007，37（1）：16-19. Qin Jie，Xu Ruilong，Qin Yang. Experimental research on prestressing construction technology of National Gymnasium[J]. Industriɑl Construction，2007，37（1）：16-19（in Chinese）.

［4］周黎光，仝为民，杜彦凯，等. 中国石油大厦双向张弦梁工程预应力施工技术[J]. 施工技术，2008，37（3）：8-11. Zhou Liguang，Tong Weimin，Du Yankai，et al. Prestress construction technology of bidirectional string structure in China Petroleum Building[J]. Construction Technology，2008，37（3）：8-11（in Chinese）.

［5］张 胜，甘 明，范 波. 安福大厦双向张弦梁设计研究[J]. 建筑结构，2006，36（6）：73-75. Zhang Sheng，Gan Ming，Fan Bo. Design and analysis of two way beam string structure in Anfu Building[J]. Building Structure，2006，36（6）：73-75（in Chinese）.

［6］秦 杰，陈新礼，徐瑞龙，等. 国家体育馆双向张弦梁结构节点设计与试验研究[J]. 工业建筑，2007，37（1）：12-15. Qin Jie，Chen Xinli，Xu Ruilong，et al. Design and experimental study on the joints of National Gymnasium [J]. Industriɑl Construction，2007，37（1）：12-15（inChinese）.

［7］尚仁杰，吴转琴，李佩勋，等. 基于平衡荷载的双向张弦梁下弦索网找形方法[J]. 工程力学，2008，25（3）：174-181. Shang Renjie，Wu Zhuanqin，Li Peixun，et al. The form-finding method based on balanced load of the down string-net of bi-directional beam-string structure[J]. Engineering Mechɑnics，2008，25（3）：174-181（in Chinese）.

［8］吴 捷，吕志涛，舒赣平. 双向张弦梁索网形状优化后的零状态找形研究[J]. 建筑结构，2013，43（增1）：356-361. Wu Jie，Lü Zhitao，Shu Ganping. Study on zero-stress state form-finding after shape optimizing of bidirectional beam string structure cable net[J]. Building Structure，2013，43（Suppl 1）：356-361（in Chinese）.

［9］Chu D N. Evolutionary Structural Optimization Method for System with Stiffness and Displacement Constraints [D]. Melbourne：Department of Civil and Building Engineering，Victoria University of Technology，1997.

［10］Gil L，Andreu A. Shape and cross-section optimization design of a truss structure[J]. Comput Struct，2001，79（7）：681-689.

［11］Wang D，Zhang W H，Jiang J S. Truss shape optimization with multiple displacement constraints[J]. Computer Methods in Applied Mechɑnics ɑnd Engineering，2002，191（33）：3597-3612.

［12］吴 捷. 影响双向张弦梁结构受力性能的参数分析[J]. 哈尔滨工业大学学报，2013，45（12）：121-128. Wu Jie. Analysis of parameters affecting mechanical performance of bidirectional beam string structure[J]. Journɑl of Hɑrbin Institute of Technology，2013，45（12）：121-128（in Chinese）.

［13］吴 捷. 双向张弦梁结构的形状优化及静动力特性研究[D]. 南京：东南大学土木工程学院，2012. Wu Jie. Study on Shape Optimization and Static and Dynamic Characteristics of Bidirectional Beam String Structure[D]. Nanjing：School of Civil Engineering，Southeast University，2012（in Chinese）.

［14］中国工程建设标准化协会. CECS127：2001 点支式玻璃幕墙工程技术规程[S]. 北京：中国标准出版社，2011. China Association for Engineering Construction Standardization. CECS127：2001 Technical Specification for Point Supported Glass Curtain Wall [S]. Beijing：The Standards Press of China，2011（in Chinese）.

［15］中华人民共和国建设部. JGJ61—2003/J258—2003 网壳结构技术规程[S]. 北京：中国标准出版社，2003. Ministry of Construction of the People's Republic of China. JGJ61—2003/J258—2003 Technical Specification for Latticed Shells[S]. Beijing：The Standards Press of China，2003（in Chinese）.

（责任编辑：赵艳静）

Cable Force Characteristic Test of Bidirectional Beam String Structure After Cable Shape Optimization

Wu Jie1, 2
（1. Gold Mantis School of Architecture，Soochow University，Suzhou 215000，China；2. School of Civil Engineering，Southeast University，Nanjing 210096，China）

Abstract：The shape of bidirectional beam string structure is determined by the balancing load value. In the test, the tension end was simulated by special turnbuckle and the anchor end was simulated by modified U type rode cappel. An experimental model of bidirectional beam sting structure after the optimization of cable shape was designed, which adopted a load scheme combining lever concentrated loading through distributive girder on multiple spots and directly hanging loading in the center of the structure plane. The test result showed that it was appropriate for the bidirectional prestressed cables, the lower part of bidirectional beam string structure, to pull step by step in two intersecting directions, with the tension sequence from midspan to the end. When the vertical load increased to the balancing load value, the force of each cable in two directions was almost equal. Cable forces were evenly distributed, which improved the cable force distribution in loading stage. The cable net of bidirectional beam sting structure was susceptible to asymmetrical live load, especially to half span load, which led to a higher force of sidespan cable than that under full span load.

Keywords：cable shape optimization；bidirectional beam string structure；tension sequence；the whole span uniform load；half long span uniform load；half short span uniform load；a quarter span uniform load

通讯作者：吴 捷，jwu@suda.edu.cn.

作者简介：吴 捷（1981— ），女，博士，讲师.

基金项目：国家自然科学基金资助项目（51208094，51508363）.

收稿日期：2014-07-05；修回日期：2014-12-05.

中图分类号：TU394

文献标志码：A

文章编号：0493-2137（2016）01-0086-10

DOI:10.11784/tdxbz201407021