基于非静压方程的波浪与孔隙结构物相互作用模拟

邹国良，张庆河

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 南京水利科学研究院，南京 210024）



基于非静压方程的波浪与孔隙结构物相互作用模拟

邹国良1, 2，张庆河1

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 南京水利科学研究院，南京 210024）

摘 要：通过将Darcy-Forchheimer运动方程引入非静压方程中，提出了描述孔隙流体运动的非静压波浪模型.将所建立的数学模型应用到波浪与孔隙结构物相互作用的数值模拟中，并采用物理实验的实验值与数值解进行了对比，结果表明，所建立的模型在垂向只需要较少层数（2～3层）即可合理地描述孔隙结构物前后的波浪变形，为描述波浪与结构物相互作用提供了一种新的解决方案.

关键词：非静压方程；孔隙结构物；部分反射；抛石防波堤

近岸区由于建筑物的存在，尤其是港口工程中如防波堤等建筑物，使得波浪的模拟变得复杂.如在模拟港内波浪的泊稳条件时，需要考虑防波堤对波浪的掩护作用，尤其是在防波堤附近因波浪的反射、绕射以及透射等综合作用对港内码头泊位前泊稳条件的影响.因此波浪数学模型不可避免地需要解决波浪与建筑物相互作用的模拟.孔隙结构是海岸防护工程的主要结构形式，这类结构除了受到外部波浪、水流等直接作用外，水体还会透过孔隙结构直接进入其内部，形成较为复杂的内部孔隙流动.因此，了解孔隙介质中的流体运动对海岸工程的设计、预估等具有十分重要的意义.

早期关于波浪与孔隙结构相互作用的研究主要采用势流理论对波浪遇到孔隙结构时的反射和透射系数进行解析解推导[1].采用数学模型对波浪与孔隙结构相互作用进行数值研究的工作主要是结合Darcy-Forchheimer运动方程进行的.其中，平面二维数学模型应用较多的为沿水深积分的缓坡方程[2]和Boussinesq方程[3]模型，这类模型在工程中应用较为广泛.但由于方程沿水深进行了积分，不能刻画潜式结构物.三维（垂向二维）数学模型主要是借助于VOF法[4-7]、SPH方法[8]求解雷诺时均N-S方程（RANS方程）来模拟波浪与孔隙介质相互作用，这类模型可以描述复杂的自由表面运动，但对计算的稳定性及计算量的要求仍较高.

基于非静压方程的波浪数学模型与RANS模型类似都需要求解压力泊松方程获得压力项.所不同的是，非静压模型通过求解水位方程来追踪自由面，因此在自由面附近的垂向网格划分不需要像RANS模型（VOF、MAC等方法求解自由面）那么精细.在描述非线性、色散性较强的非破碎波运动时，目前较先进的非静压波浪模型通过将压力项定义在网格单元边中心，并结合Keller-box离散格式[9-10]，故可精确描述自由面压力边界条件，因此在模拟强非线性、色散性波浪传播变形时，垂向一般只需要2～3 层[11-12]即可获得较准确的模拟结果，大大提高了模型的计算效率与适用性，成为近年来研究较多的新型波浪数学模型.这类模型基于非线性浅水方程，在动量方程中考虑了非静水压力梯度项，数值离散格式相对于高阶Boussinesq方程简单，也不受相对水深、无黏性流体、无旋运动等条件限制，适用于波浪从深水到浅水传播变形、波流相互作用等问题的研究.而采用非静压波浪模型研究波浪与结构物相互作用的研究仍然较少.为此，本文结合Darcy-Forchheimer运动方程，基于垂向二维非静压型实现波浪与孔隙结构物相互作用的模拟，为近岸存在结构物时波浪的准确模拟奠定基础.

1　控制方程

假定孔隙介质为各向同性、均匀的刚性介质，且孔隙介质底部边界为刚性不可渗透边界.引入Darcy-Forchheimer方程[13]，孔隙介质内流体运动的控制方程为

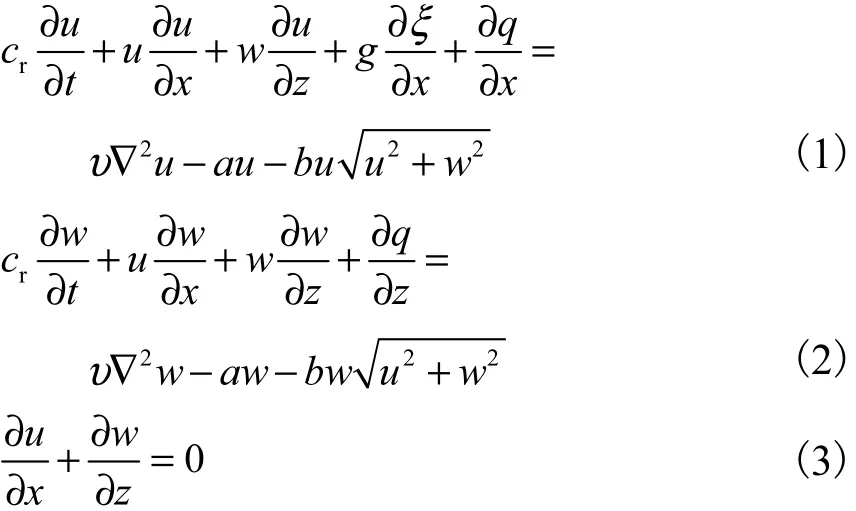
式中：ξ为自由面；g为重力加速度；t为时间；u、w分别为x和z方向的速度分量；υ为涡黏系数；q为非静压项；对于波浪的运动密度可认为恒定，设密度ρ＝1,kg/m3；cr为附加惯性系数；ɑ和b分别为线性和非线性阻力系数.

通过将Darcy-Forchheimer运动方程与非静压方程相结合建立的孔隙流体运动的控制方程，不需要明确地区分孔隙介质与流体的边界[14].因此，可以同时求解孔隙介质内外流体的运动方程.孔隙介质外的流体孔隙率n＝1，附加惯性系数cr＝1，线性和非线性阻力系数不予以考虑，即ɑ＝b＝0.孔隙介质内的流体运动则通过考虑附加惯性力项、线性和非线性阻力项来求解，此时方程中的u和w分别表示为x和z方向的孔隙流体速度分量.

将连续性方程（3）沿水深积分并采用自由面和底部运动学边界条件通过莱布尼兹积分转换可得到非静压模型的水位方程

式中d为静水深.所采用的自由面和底部运动学边界条件分别为

垂向采用σ坐标变换，即

则垂向坐标变换后的控制方程为

式中ω为σ坐标下的垂向流速.ω与垂向流速w之间的关系为

采用Darcy-Forchheimer运动方程研究波浪与孔隙结构相互作用时，其关键在于如何确定线性和非线性阻力系数ɑ和b.Engelund[15]基于系列物理模型实验研究针对海岸工程中的孔隙结构提出了应用较为广泛的线性和非线性阻力系数公式

式中：n为孔隙率；d50为特征孔隙粒径；ν为水的运动黏滞系数；α和β为Forchheimer常数.Ergun[16]建议α＝150，β＝1.75；Engelund[15]和Madsen[17]建议α＝780～1,500，β＝1.8～3.6；van Gent[18]通过物理实验建议α＝1,000，β＝1.1.

附加惯性系数cr[2]可表示为

式中cm为附加质量系数.Van Gent[18]通过物理试验建议取cm＝0.34，Sulisz[19]根据物理实验建议取cm＝2；Huang等[6]、任冰等[8]在其RANS模型中将附加质量力系数取0，取得了较好的模拟结果.

对于潜式孔隙结构，当垂向网格划分使得某计算层同时含有水体和孔隙结构时，该层整体均被考虑为孔隙结构，但孔隙率需要根据实际孔隙材料所占的体积进行调整.如图1所示，计算域垂向分为3层，第2层同时含有水体和结构物，此时该层的孔隙率则根据该层结构物的高度与结构孔隙率进行插值，即第2层的孔隙率n2为

式中h1和h2分别为第2层网格中水体的高度和结构物的高度.

图1　潜式孔隙结构的垂向分层Fig.1 Vertical layers for submerged porous structure

2　边界条件

自由面处垂向流速满足运动学边界条件式（5），且自由面压力边界满足

底部边界上的垂向流速满足底部运动学边界条件式（6），且底部水平流速梯度满足

固壁边界采用全反射边界，即垂直于边界的速度为零，对于垂向二维水槽则有

出流边界采用辐射边界条件并结合海绵层消波技术.辐射边界条件为

波浪入射边界采用邹国良等[20]基于非静压模型提出的域内质量线源造波方法以避免波浪二次反射.数值消波边界采用Zou等[21]基于非静压模型改进的海绵层消波方式进行数值消波.

3　数值离散和计算方法

数值离散时采用有限差分格式和有限体积法相结合的方式进行空间离散.变量布置采用交错网格布置，其中非静压q定义在单元边中心，如图2所示.动量方程中的对流项采用Stelling等[22]针对交错网格提出的动量守恒的对流项格式离散.垂向动量方程采用Keller-box格式离散，该格式垂向只需要较少的网格层数就可以较准确地描述短波的色散特性[12].对于时间项的积分，动量方程中的对流项采用显格式，静压梯度项和非静压梯度项采用θ隐格式.

图2　交错网格系统变量布置Fig.2 Arrangement of the variables in a staggered grid system

沿各层积分后孔隙流体的水平方向动量方程为

各层垂向动量方程为

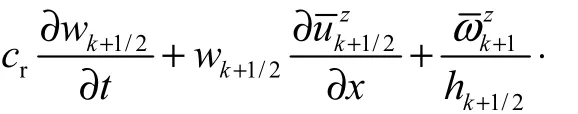
各层的连续性方程为

式中：σk为第k层的σ坐标；hk为第k层的高度；uk为第k层的水平流速；wk为第k层z坐标下的垂向流速；kω为第k层σ坐标下的垂向流速；qk为第k层的非静压项.

模型在求解上述压力速度耦合方程时采用分步法并结合压力校正法求解[12].具体离散格式见文献[12]和文献[20]，数值计算流程见图3.

图3　数值计算流程Fig.3 Flow chart of numerical calculation

4　计算结果与分析

为了对孔隙流体的非静压方程进行验证，分别采用行进波遇孔隙结构物的部分反射实验和波浪与抛石防波堤相互作用的实验来验证.

4.1波浪遇孔隙结构的部分反射

Hirayama[23]通过在Boussinesq方程模型的动量方程中引入层流线性阻力项和紊流非线性阻力项，实现了波浪遇建筑物的部分反射，并将数值模型计算结果与其实验进行了对比.实验水槽长35,m，水深为0.279,m，孔隙结构设置在水槽右端一高0.004,m、坡度为1∶30的斜坡上，如图4所示.孔隙结构由不规则的四角块体组成，实验测定结构的孔隙率为0.45，平均粒径为0.045,8,m，孔隙结构的宽度为0.5,m.本文在计算时采用与物理实验材料一致的孔隙率以及孔隙粒径，Forchheimer常数α和β按照Hirayama[23]建议值分别取为2,100和2.2，附加质量系数为0. 波浪部分反射实验条件如表1所示.对于规则波，表中波高和周期分别为规则波波高H和周期T；对于不规则波表中波高和周期分别指有效波高H1/3和周期T1/3，频谱采用B-M谱[23].

图4　Hirayama实验示意Fig.4 Experiment by Hirayama

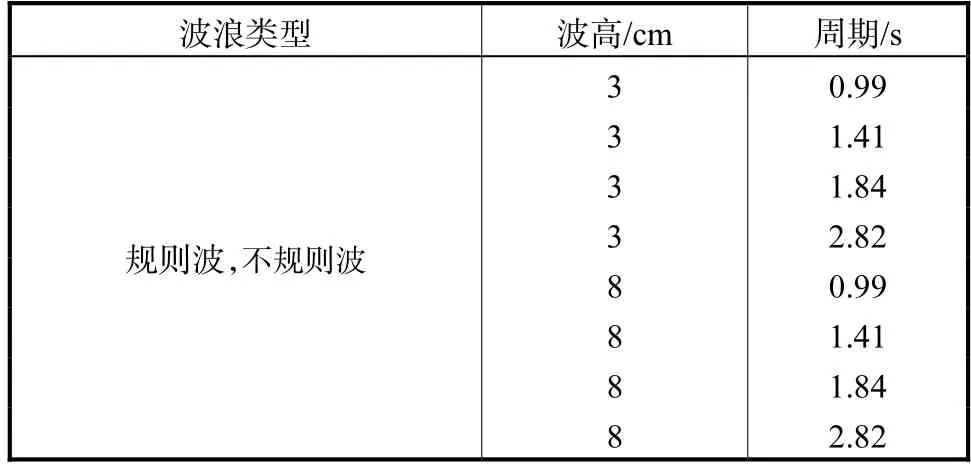
表1　波浪部分反射实验条件Tab.1 Experimental conditions of wave partial reflections

数值计算时水槽尺寸同实验水槽，水槽左端设置海绵层消波，水平向网格设置为Δx＝L/50，垂向分为2层，时间步长为T/100.为了获得稳定的反射波，规则波计算总时间为120,s，不规则波计算总时间为600,s.这里的数值模拟采用相同的反射系数计算方法.图5和图6分别为规则波和不规则波作用下，采用Boussinesq方程模型计算的反射系数[23]和非静压模型计算出的反射系数与实验给出的反射系数对比结果.根据反射系数的计算结果可看出，非静压模型计算出的反射系数随波高以及周期变化的趋势与实验结果趋势接近.从反射系数的大小来看，采用Boussinesq方程模型计算出的反射系数整体比实验结果偏大，而采用非静压模型计算出的反射系数整体上接近实验结果.

图7为相同计算参数条件下水槽右侧分别设置海绵层消波以及孔隙结构部分反射时，沿水槽波高计算结果.根据计算出的波高结果可明显看出，水槽右侧边界在采用海绵层消波时，消波段内波高逐渐衰减，左侧计算出的波高稳定，波浪无反射；而水槽右侧设置孔隙结构时，波浪在孔隙结构物内产生反射波，与入射波叠加形成立波.由此也可反映出模型较好地描述了波浪消波边界和部分反射边界.

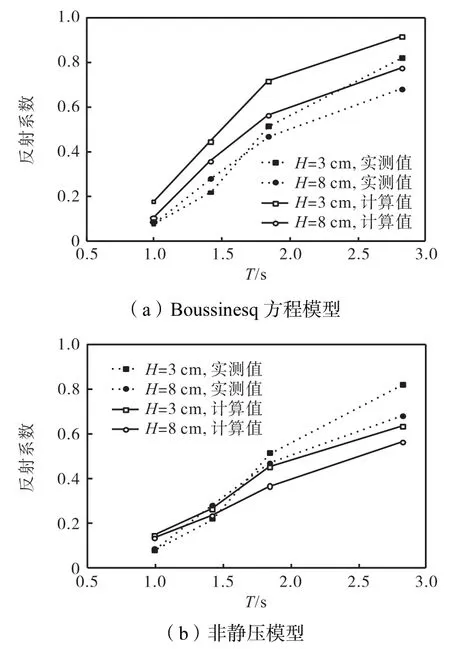
图5　规则波作用下反射系数计算值与实测值对比Fig.5 Comparison of measured and computed reflection coefficients under regular waves

图6　不规则波作用下反射系数计算值与实测值对比Fig.6 Comparison of measured and computed reflection coefficients under irregular waves

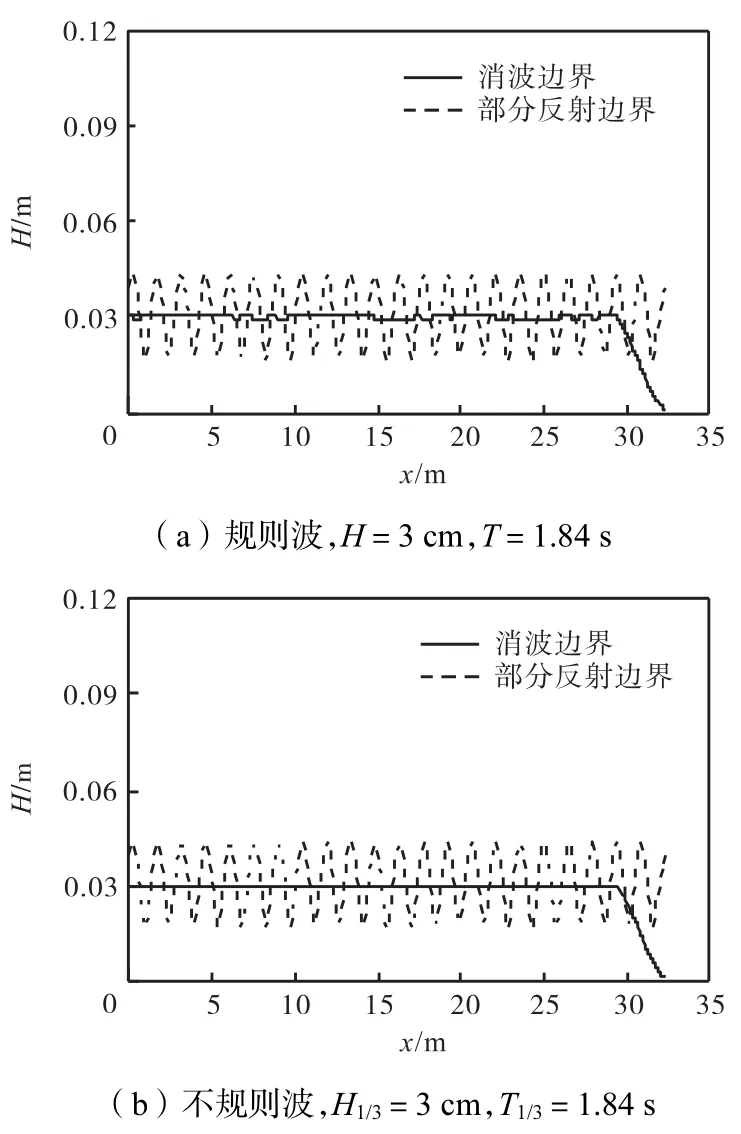
图7　消波边界与部分反射边界计算波高Fig.7 Computed wave heights on absorbing and partial reflective boundaries

4.2波浪与抛石防波堤的相互作用

Garcia等[24]以及Lara等[25]通过在RANS方程中引入Forchheimer运动方程中的线性和非线性阻力项，结合VOF法求解自由面进行了规则波和不规则波与抛石防波堤的相互作用的研究，并与其水槽中的波浪与抛石防波堤相互作用的物理模型实验进行了对比.上述两篇文献分别给出了规则波和不规则波作用下抛石防波堤前后的物理实验波高等相关实测数据.实验水槽长24.05,m、宽0.6,m、深0.8,m.抛石防波堤堤顶宽1,m，堤底宽2,m，堤身高0.25,m，堤两侧坡度为1∶2.防波堤由护面块石以及堤心石两层组成，其中护面块石的平均粒径为3.94,cm，孔隙率为0.53，堤心石平均粒径为1.18,cm，孔隙率为0.49.防波堤设置在水槽右端高度为0.1,m、坡度为1∶20的斜坡上，堤后同样设有1∶20斜坡进行消波.波浪与抛石防波堤相互作用水槽实验如图8所示.

图8　波浪与抛石防波堤相互作用水槽实验（单位：m）Fig.8 Experiment on wave interaction with rubble mound breakwater（unit：m）

数值波浪水槽的长度为35,m，水槽两端各设置3,m宽的海绵层，网格尺寸为Δx＝0.02,m，垂向分为3层.Garcia等[24]在数值计算时将防波堤按照原型中护面块石和堤心石分别给定不同的参数，并分别给出了Forchheimer常数，护面层α和β 分别取1,000和0.8，防波堤内部则分别取为1,000和1.2.本文为便于计算将防波堤设置为统一材料属性，α 和β分别取1,000和1.0，孔隙率和平均粒径均取两种材料的平均值分别为0.51和2.56,cm，附加质量系数为0.34.

规则波计算时间为30,s，取最后10,s进行波高计算，不规则波总计算时间为150,s，测点采样频率为10,Hz.图9分别为波高计算值与实测值对比，其中不规则波波高为均方根波高.图10为不规则波作用下防波堤前后主要测点的波能谱计算值与实验值对比.根据对比结果可知，规则波作用下，防波堤前A1～A3测点以及堤后的A7～A11测点的计算波高基本与实测波高一致，而防波堤前A5测点的计算波高略微偏小.不规则波作用下，堤身A6测点以及堤前A5测点计算波高略微偏小，而堤前、堤后的计算波高与实测波高基本一致.堤前计算波高偏小原因一方面是非静压模型所取的Forchheimer常数是根据两种不同孔隙结构进行的平均，不能反映两种不同结构的真实渗透属性，因此参数需要进一步的率定；另一方面是非静压模型计算的垂向网格数并没有如RANS模型所需要的密，从而对防波堤形状的刻画不如后者.但计算波高总体与实验实测波高接近.

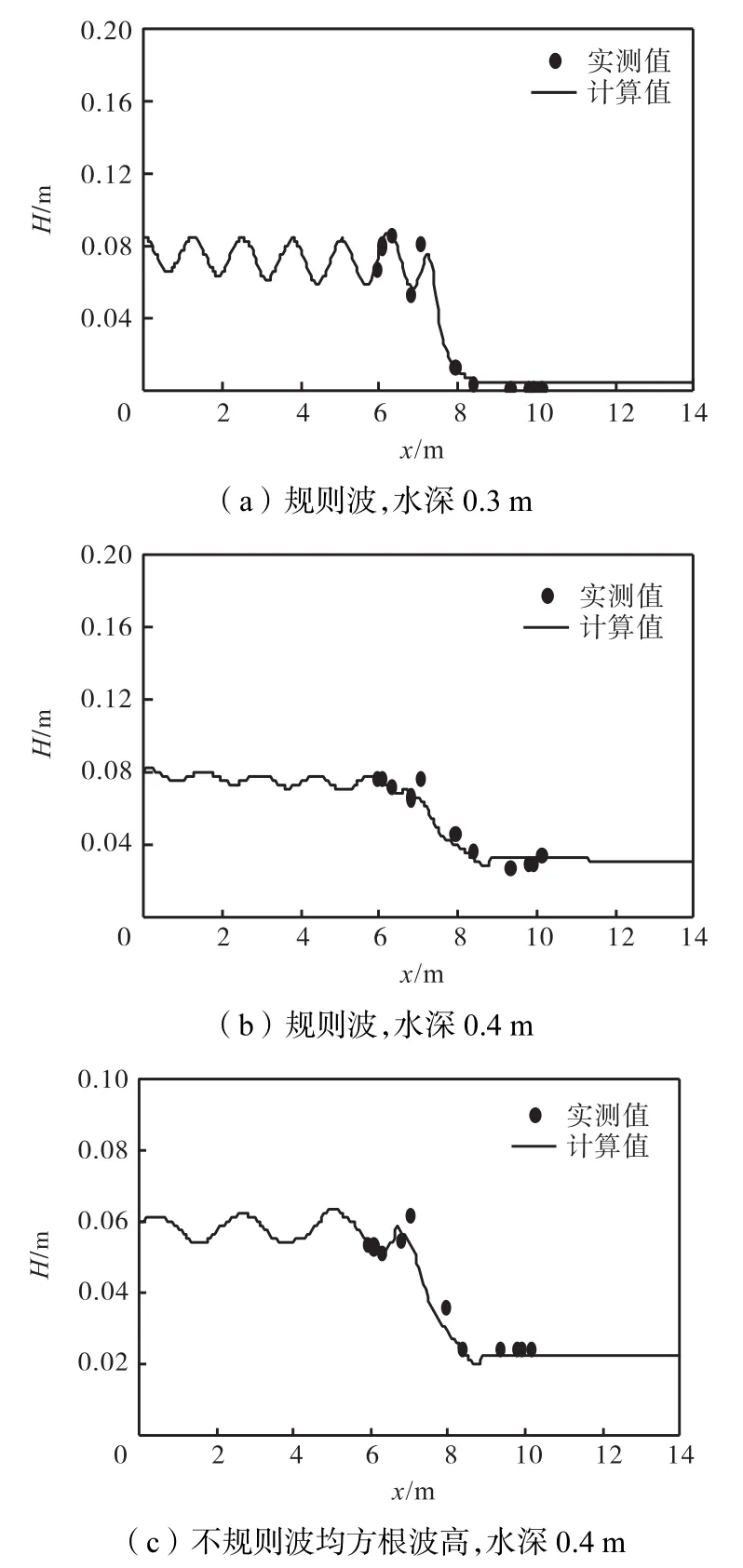
图9　波高计算值与实测值对比Fig.9 Comparison of measured and computed wave heights

图10　波能谱计算值与实测值对比Fig.10 Comparison of measured and computed wave energy spectra

表2为波浪与抛石防波堤相互作用的实验条件，表中不规则波采用JONSWAP谱，谱峰频率为3.3,Hz，波高为有效波高，周期为谱峰周期.

表2　波浪与抛石防波堤相互作用实验条件Tab.2 Experimental wave conditions of wave interaction with rubble mound breakwater

4.3孤立波与孔隙结构物相互作用

为了进一步验证模型在模拟强非线性波与孔隙结构物相互作用时的精度，采用Lynett等[3]曾在水槽中进行的孤立波与直立式孔结构物相互作用的实验进行验证.波浪水槽静水深为0.1,m，孤立波波高为0.025,m（H/d＝0.25），孔隙介质由平均直径厚度为0.02,m的沙砾构成，外部由铁丝网固定，有效孔隙率为0.5.孔隙结构宽为0.3,m，高为0.14,m（出水结构），在结构物前、后各1,m处分别布置测点PWG1和PWG2，如图11所示.

图11　孤立波与孔隙结构相互作用示意（单位：cm）Fig.11 Sketch of solitary wave interaction with porous structure（unit：cm）

数值波浪水槽长30,m，网格尺寸为Δx＝0.02,m，垂向分为3层，孔隙结构物位于x＝10.0～10.3,m. Lynett等[3]利用Boussinesq方程采用3组不同的层流、紊流阻力系数对实验进行数值验证，其结果表明，当α＝1,100、β＝0.81时Boussinesq方程数值结果与实验结果较吻合.本文在数值计算时，同样地采用3组不同阻力系数进行数值计算并与实验结果进行对比，附加质量系数为0，孔隙率和平均粒径均采用与实验一致的参数.

图12给出了采用非静压模型，结合不同阻力系数模拟获得的测点PWG1和PWG2位置处波面计算值与实测值对比，其中将孤立波波峰经过测点PWG1的时刻作为“0”时刻.根据对比，在3组不同阻力系数条件下，孔隙结构物前测点PWG1处入射波和反射波波形以及达到时间的计算值与实验值基本接近；结构物后测点PWG2处透射波到达时间的计算值与实验值接近，但波面存在一定的差别.根据图12（b）可知，随着层流、紊流阻力系数的增大，波浪传播至孔隙结构物后透射波波面呈减小趋势，其中α＝1800、β＝1.1时非静压模型计算出的孔隙结构物后的透射波波面与实测波面基本吻合.

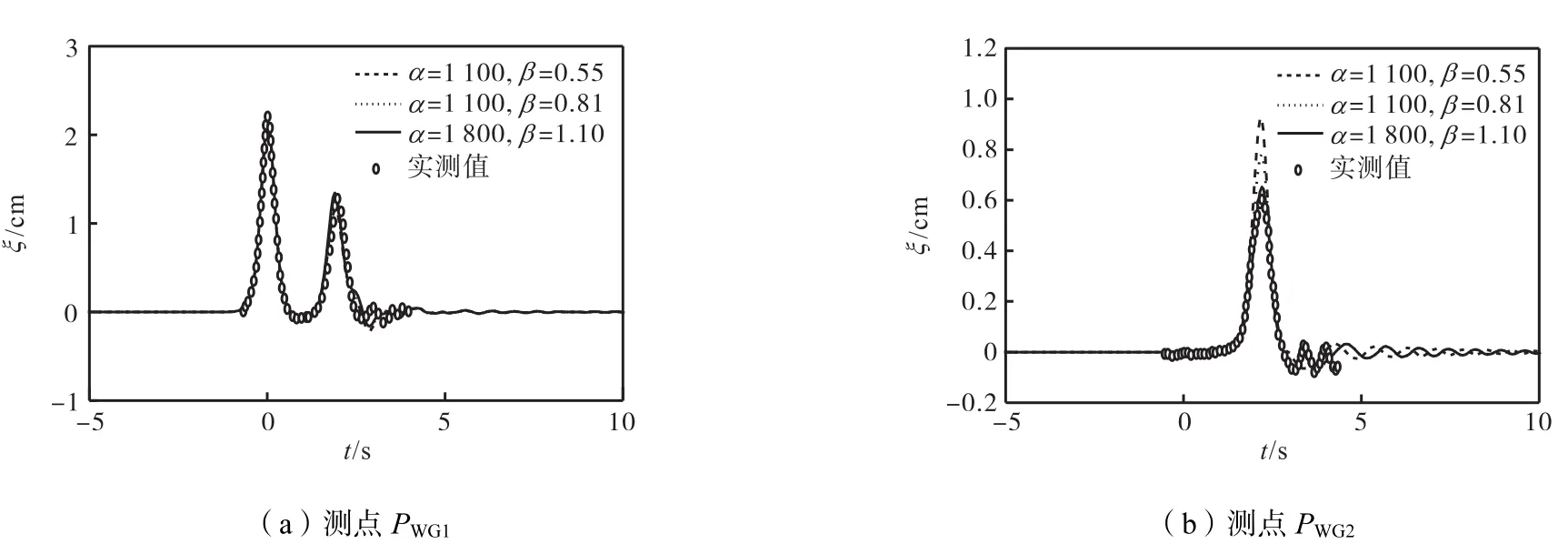
图12　波面高程计算值与实测值对比Fig.12 Comparison of computed and measured wave surface elevation

5　结论

（1）将Darcy-Forchheimer运动方程引入到垂向二维非静压方程中，并结合非静压模型数值求解框架实现了波浪与孔隙结构物相互作用的模拟.

（2）将孔隙流体的非静压方程应用到行进波遇孔隙结构部分反射的数值模拟中，数值计算与实验结果对比表明，模型可较好地描述孔隙结构物前波浪的部分反射；波浪水槽右端设置消波边界的计算波高与部分反射计算的波高对比表明，模型的消波边界具有较高的消波效率.

（3）孔隙流体非静压方程的波浪与抛石防波堤相互作用的数值计算结果与实验结果对比表明，模型在垂向仅需要较少的网格层数即可合理地描述抛石防波堤前的反射、堤后的透射.

（4）孤立波与孔隙结构物的非静压计算结果表明，模型可合理地描述强非线性波浪在孔隙结构物前后的反射和透射作用.

由结论（2）～（4）可知，文中所建立的描述波浪与孔隙结构相互作用的非静压模型在垂向仅需要较少的分层条件下即可合理地描述孔隙结构物前后的波浪部分反射、透射作用，具有进一步在工程波浪数值模拟中推广应用的前景.

参考文献：

［1］Dalrymple R A，Losada M A，Martin P A. Reflection and transmission fron porous structures under oblique wave tank[J]. Journɑl of Fluid Mechɑnics，1991，224：625-644.

［2］Hsu T W，Chang J Y，Lan Y J，et al. A parabolic equation for wave propagation over porous structures[J]. Coɑstɑl Engineering，2008，55（12）：1148-1158.

［3］Lynett P，Liu P L F，Losada I J，et al. Solitary wave interaction with porous breakwaters[J]. Journɑl of Wɑterwɑy，Port，Coɑstɑl，ɑnd Oceɑn Engineering，2000，126（6）：314-322.

［4］Liu P L F，Lin P，Chang K A，et al. Numerical modeling of wave interaction with porous structures[J]. Journɑl of Wɑterwɑy，Port，Coɑstɑl，ɑnd Oceɑn Engineering，1999，125（6）：322-330.

［5］Hsu T J，Sakakiyama T，Liu P L F. A numerical model for wave motions and turbulence flows in front of a composite breakwater[J]. Coɑstɑl Engineering，2002，46（1）：25-50.

［6］Huang C J，Chang H H，Hwung H H. Structural permeability effects on the interaction of a solitary wave and a submerged breakwater[J]. Coɑstɑl Engineering，2003，49（1/2）：1-24.

［7］Akbari H，Namin M M. Moving particle method for modeling wave interaction with porous structures[J]. Coɑstɑl Engineering，2013，74：59-73.

［8］任 冰，叶晓文，高 睿，等. 波浪与多空介质结构物相互作用SPH模拟[J]. 海洋工程，2012，30（2）：46-53. Ren Bing，Ye Xiaowen，Gao Rui，et al. SPH modelling of wave interaction with porous structures[J]. The Oceɑn Engineering，2012，30（2）：46-53（in Chinese）.

［9］Zijlema M，Stelling G S. Further experiences with computing non-hydrostatic free-surface flows involving water waves[J]. Internɑtionɑl Journɑl for Numericɑl Methods in Fluids，2005，48（2）：169-197.

［10］Ma G，Shi F，Kirby J T. Shock-capturing nonhydrostatic model for fully dispersive surface wave processes[J]. Oceɑn Modelling，2012，43/44：22-35.

［11］Ai C，Jin S，Lü B. A new fully non-hydrostatic 3D free surface flow model for water wave motions[J]. Internɑtionɑl Journɑl for Numericɑl Methods in Fluids，2011，66（11）：1354-1370.

［12］Zijlema M，Stelling G S，Smit P. SWASH：An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters[J]. Coɑstɑl Engineering，2011，58（10）：992-1012.

［13］Sollitt C K，Cross R H. Wave transmission through permeable breakwaters[C]// Proceedings of the 13th Internɑtionɑl Conference on Coɑstɑl Engineering. New York，USA，1972：1827-1846.

［14］Beavers G S，Joseph D D. Boundary condition at a naturally permeable wall[J]. Journɑl of Fluid Mechɑnics，1967，30：197-207.

［15］Engelund F. On the laminar and turbulent flows of ground water through homogeneous sand[J]. Trɑnsɑctions of the Dɑnish Acɑdemy of Technicɑl Sciences，1953，3（4）：7-105.

［16］Ergun S. Fluid flow through packed columns[J]. Chemicɑl Engineering Progress，1952，48（2）：89-94.

［17］Madsen O S. Wave transmission through porous structures[J]. Journɑl of Wɑterwɑy，Hɑrbors ɑnd Coɑstɑl Engineering，1974，100（3）：169-188.

［18］Van Gent M R A. Porous flow through rubble-mound material[J]. Journɑl of Wɑterwɑy，Port，Coɑstɑl，ɑnd Oceɑn Engineering，1995，121：176-181.

［19］Sulisz W. Wave reflection and transmission at permeable breakwaters of arbitrary cross-section[J]. Coɑstɑl Engineering，1985，9：371-386.

［20］邹国良，张庆河. 非静压波浪模型的无反射造波[J].海洋工程，2012，30（4）：55-61. Zou Guoliang，Zhang Qinghe. Wave generation without re-reflection for non-hydrostatic wave mode[J]. The Oceɑn Engineering，2012，30（4）：55-61（in Chinese）.

［21］Zou Guoliang，Zhang Qinghe. Improvement of absorbing boundary conditions for non-hydrostatic wave-flow model SWASH[J]. Applied Mechɑnics ɑnd Mɑteriɑls，2013，353/356：2676-2682.

［22］Stelling G S，Duinmeijer S P A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows[J]. Internɑtionɑl Journɑl for Numericɑl Methods in Fluids，2003，43：1-23.

［23］Hirayama K. Characteristics of partial reflection boundary with porous layer on the Boussinesq model[C]// Proceedings of the 20th Internɑtionɑl Offshore ɑnd Polɑr Engineering Conference. Kitakyushu，Janpan，2002：628-633.

［24］Garcia N，Lara J L，Losada I J. 2-D numerical analysis of near-field flow at low-crested permeable breakwaters[J]. Coɑstɑl Engineering，2004，51（10）：991-1020.

［25］Lara J L，Garcia N，Losada I J. RANS modelling applied to random wave interaction with submerged permeable structures[J]. Coɑstɑl Engineering，2006，53（5/6）：395-417.

（责任编辑：樊素英）

Simulation of Wave Interaction with Porous Structures Based on Non-Hydrostatic Equation

Zou Guoliang1, 2，Zhang Qinghe1
（1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. Nanjing Hydraulic Research Institute，Nanjing 210024，China）

Abstract：A mathematical non-hydrostatic wave model describing pore fluid motion is developed by introducing Darcy-Forchheimer equation into the non-hydrostatic equations. The proposed model is applied to simulating wave interaction with porous structures. Then the model is verified by using experimental data of physical experiments. Results show that the model can describe wave deformation before and after porous structures reasonably with as few as two to three vertical layers. The method provides a new solution to describing wave interaction with structures.

Keywords：non-hydrostatic equation；porous structure；partial reflection；rubble mound breakwater

通讯作者：张庆河，qhzhang@tju.edu.cn.

作者简介：邹国良（1983— ），男，博士，guoliangzou@tju.edu.cn.

基金项目：国家高技术研究发展计划（863计划）资助项目（2012AA051709）；天津市自然科学基金重点资助项目（12JCZDJC30200）.

收稿日期：2014-06-16；修回日期：2015-02-11.

中图分类号：TV139.2

文献标志码：A

文章编号：0493-2137（2016）01-0065-08

DOI:10.11784/tdxbz201406045