基于B样条参数化描述的形状扩散光学层析成像方法
2016-03-18赵会娟刘玲玲武林会贾梦宇
赵会娟,刘玲玲,刘 明,武林会,王 媛,贾梦宇,高 峰
(1. 天津大学精密仪器与光电子工程学院,天津 300072;2. 天津市生物医学检测技术与仪器重点实验室,天津 300072)
基于B样条参数化描述的形状扩散光学层析成像方法
赵会娟1, 2,刘玲玲1,刘 明1,武林会1,王 媛1,贾梦宇1,高 峰1, 2
(1. 天津大学精密仪器与光电子工程学院,天津 300072;2. 天津市生物医学检测技术与仪器重点实验室,天津 300072)
摘 要:为了改善扩散光学层析成像(DOT)逆问题的病态性,本文发展了一种基于B样条参数化描述的形状DOT重建算法.在合理地假设组织体各区域光学参数均匀分布的前提下,通过采用B样条参数化描述复杂区域的边界,将DOT的逆问题从大规模的体元光学参数重建转化为只重建各子区域的一组光学参数和复杂形状参数.在信噪比为35,dB条件下对不同形状模拟异质体的重建结果表明,该算法在不同的光学参数范围、异质体初始形状估计、光学参数初始估计下,均可有效地重建出异质体的形状和光学参数.稳态DOT系统的仿体实验验证表明,背景光学参数和异质体光学参数的重构误差分别小于1.18%和12.00%.该算法将对肿瘤诊断漫射光层析成像的发展具有推动作用.
关键词:扩散光学层析成像;基于形状重构算法;B样条参数化;边界元法
网络出版时间:2014-10-24. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20141024.1412.001.html.
扩散光学层析成像(diffuse optical tomography,DOT)技术因其可获得与组织体生理、病理情况密切相关的功能信息而备受关注[1].为了实现较高的空间分辨率,可以使用仿CT式扫描方法[2]增加光学测量数据量,但传统的基于体元的DOT图像重建算法依然需将重建区域进行高密度剖分.由于该过程引入了大量未知参数而导致DOT逆问题呈现高度的病态性,严重影响了重建结果的精度和灵敏度[3].为了改善这一问题,基于形状的DOT重建算法应运而生,该方法将成像组织体划分为若干个子区域,在每个子区域内假设光学参数是均匀分布的,应用边界元法只剖分各区域的边界信息,使逆问题从大规模的体元光学参数重建转化为只重建各子区域的光学参数及形状参数,由于未知量个数大幅度减少,从而改善了DOT逆问题的病态性[4-6].在形状DOT重建算法研究方面,Kirsch[7]和Kress等[8]针对散射目标率进行了研究,结果表明相较于传统的基于体元的方法,基于形状的重构方法重建时间短且精度更高.为适应临床上面临的不规则异质体,并考虑到重建出各子区域的吸收系数更加具有临床意义,Zacharopoulos等[4]提出利用傅里叶级数展开法描述异质体边界,然而由于傅里叶基函数不具备局部支撑性能,因此当某个形状参数发生微扰时,重建出的边界会发生整体变化.
B样条基函数具有局部支撑性,单个控制点的改变只会影响与其相邻的曲线.且B样条曲线具有解析表达式,易实现异质体形状的描述.为此,笔者提出了利用B样条曲线描述不规则异质体形状,并发展了基于B样条参数化描述的形状DOT重建算法.
1 理论和方法
1.1基于边界元法的正问题
假设组织体中只包含1个异质体且组织体各子区域光学参数均匀分布[9],如图1所示.应用扩散方程(DE)作为描述光在组织体中传输的数学模型,其稳态形式表示如下:
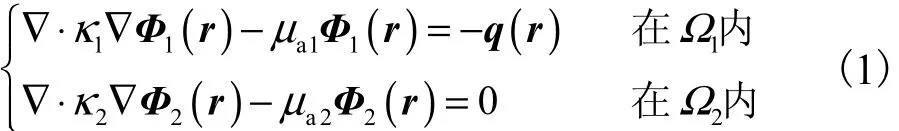
式中:1Ω为组织的背景区域;2Ω为目标或称为异质体区域;()
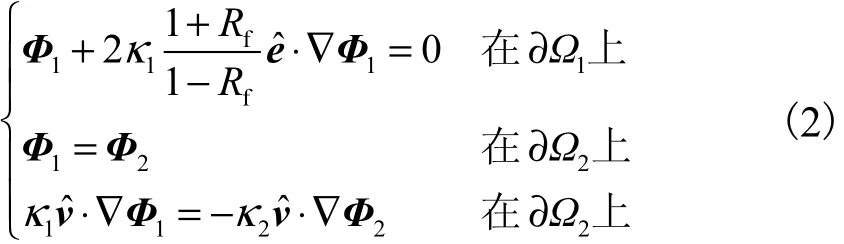
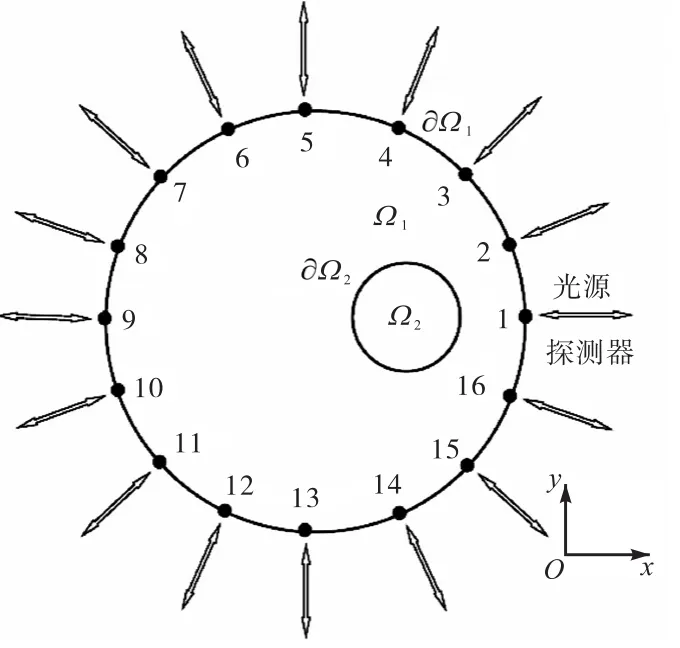
图1 单目标组织体模型的结构及源-探分布Fig.1 Structure of the tissue model with a single target,and the arrangement of the sources and detectors
采用边界元法数值求解DE,最终表面输出光流量将仅与异质体外边界的形状参数{γ }及各区域的光学参数{μa, μs′ }相关.将边界上的光子密度和光流量用离散节点上的量进行线性表示,即可得到线性方程[5].式中:系数矩阵;j是边界1Ω∂上的离散节点数目;k是边界2Ω∂上的离散节点数目;Ψ是光子密度和光流量的集合;Q是光源项.

1.2基于B样条曲线的边界形状描述
由于B样条具有局部支撑性,每个样条曲线段仅受n+1个控制点影响,因此,改动1个点,最多影响以该点为中心的总共n+1段曲线的形状.假设组织体各子区域的边界互不相交,对于二维模型,采用B样条曲线描述异质体边界2Ω∂.B样条曲线采用分段定义,如果给定m+n个控制点就可以定义m段n次的参数曲线,连接全部曲线段所组成的整条曲线称为n次B样条曲线.一般的规律是:B样条曲线的次数越低,所形成的B样条曲线就越靠近它的控制多边形,常见的包括二次B样条曲线和三次B样条曲线.考虑到B样条曲线的连续性,本文采用三次B样条曲线来描述异质体形状,即n=3.
为了方便计算,实现计算过程的简化,选用均匀B样条曲线,即节点沿参数轴均匀分布,所有节点的区间长度为常数.例如将异质体的边界剖分成32个点时,可取8个曲线段(即m=8)使各段有4个节点.已知B样条曲线控制点的个数满足关系m+ n,因此对于三次B样条一共有11个控制点.对于第i段三次B样条曲线Pi,3(u),其表达式为

式中u是自变量.
由于子区域的边界是单连通闭合曲线,且B样条基函数具有周期性,因而,前3个控制点与后3个控制点重合,即,此时,重建形状参数时只需重构8组不同的控制点坐标即可.
1.3基于形状的DOT图像重建
由于实际测量中难以对光源的实时光强、光纤与组织体的耦合系数、系统内各部分的衰减比进行精确标定,DOT技术通常采用差分测量模式[10],即将相同测量点上对实际非均匀组织的测量值除以对均匀组织的测量值作为新的测量数据.根据这一实际情况,本文中的正向算子和测量数据均采用相对数据.
本文利用Jacobi矩阵的信息,使用Levenberg-Marquardt算法构建未知量的迭代方向,实现同时重构背景的光学参数、异质体的光学参数及异质体的形状参数(二维模型里每个控制点的坐标为x和y),对于三次B样条曲线11个控制点,共需重建20个变量.而传统的基于体元的DOT技术,半径为20,mm的区域一般需被离散成1,261个节点,即使只重构吸收系数也会有1,261个变量.由此可知,B样条参数化描述的形状DOT重建技术可使未知量的个数大幅度减少,随着逆问题的规模而相应减小,将大幅度降低逆问题的病态性.
2 数值模拟验证结果
在数值模拟中,为了避免“诡问题”[11]的发生,本文中的“测量数据”由有限元法数值求解方法获得.
2.1不同重建方法的比较
圆形异质体的结构如图1所示,背景组织的半径为20,mm,圆心位于原点.异质体子区域的半径为5,mm,圆心位于(10,mm,0,mm).背景的光学参数μa1=0.004,mm-1、μs′1=0.8,mm-1,异质体的光学参数μa2=0.010,mm-1、μs′2=2.0,mm-1.假设16个光源与16个探测器均匀地分布在边界∂Ω1周围.采用边界元法处理正问题时,边界∂Ω1和∂Ω2分别被离散成60个节点和32个节点.为了模拟DOT系统测量的实际情况,在测量数据中加入高斯噪声,使得信噪比(SNR)为35,dB[12].
为了比较基于体元的DOT算法、基于傅里叶级数展开法描述的形状图像重建算法[13]和基于B样条参数化描述的形状图像重建算法,对图1所示的组织模型进行图像重建,重建结果如图2所示.表1为两种形状DOT重建算法重建出的光学参数.
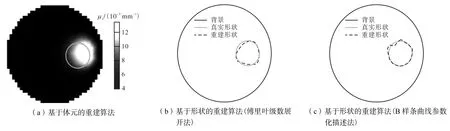
图2 采用不同算法对图1模型的重构结果Fig.2 Reconstructed results of the tissue model in Fig.1 with the DOT reconstruction algorithm based on different algorithms
从图2可知,基于体元DOT重建算法重建出的异质体偏向边界,且重建出的吸收系数相对误差大于30%.而两种形状图像重建算法都能较好地实现异质体的定位,但由于傅里叶基函数不具备局部支撑性能,当某个形状参数发生微扰时,重建的异质体形状整体上与目标的形状有较大差异.而由于B样条基函数具有局部支撑性,重建出的异质体只是在部分区域出现偏差.从表1可见,基于B样条参数化描述的形状DOT算法所获得的光学参数重建精度更高.
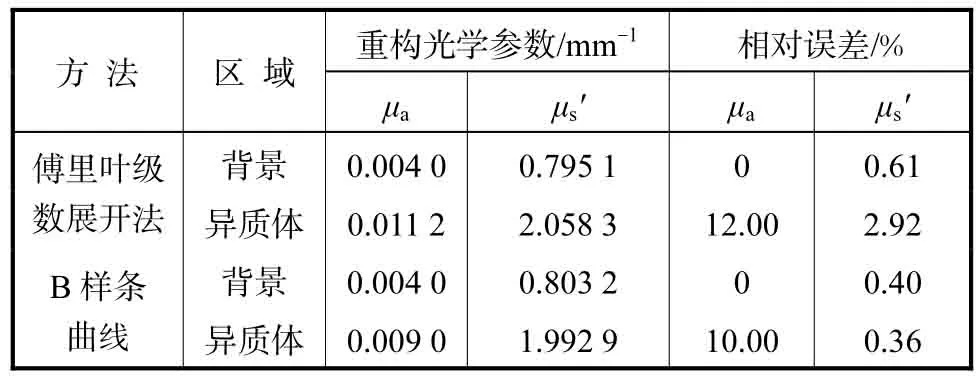
表1 两种形状DOT算法重构的光学参数比较Tab.1 Reconstructed optical parameters with two shape description DOT algorithms
2.2椭圆异质体的重建结果
含有椭圆形异质体的组织模型的拓扑结构如图3(a)所示,异质体的半轴长分别为ɑ=5,mm、b=4,mm,椭圆的原点(x0,y0)坐标为(10,mm,0,mm),椭圆相对于x正半轴的逆时针旋转角度为β=300°,其他参数与图1的相同.
在信噪比为35,dB下,基于B样条参数化描述的形状图像重建算法经过20次迭代之后的重建结果如图3(b)所示.为了分析算法对形状和光学参数的重建过程,分别定义面积比(AR)、距离标准化参数(LR)和残差(RE).AR定义为重构异质体的面积与实际异质体面积的比值;LR为重构点与实际点的距离标准化参数;TRE=rs⋅ rs,其中,rs矩阵是正向算子和测量数据的相对误差.面积比和残差随迭代次数的变化分别如图3(c)、(d)所示,结果表明,20次迭代之后的面积比为100.8%,最大和最小LR分别为0.134 3和0.090 1,说明采用本文发展的算法可以很好地重构出异质体形状.
对于不同大小的异质体和初始尺寸设置,结果表明,该算法均能够有效地进行图像重构,背景和异质体光学参数重构误差分别小于2.5%和7.0%.
为了验证算法的普适性,在不同的初始光学参数设置内进行重构,结果表明,当初值光学参数设置为真实光学参数的0.2~1.5倍之间时,背景光学参数重构误差小于0.44%,异质体光学参数重构误差小于6.00%.由于篇幅的限制,这些结果未在本文列出.
在图1所示的组织模型内嵌1个不规则形状的异质体,如图4(a)所示,采用B样条曲线描述该异质体的形状,即

其他参数的设置与第2.2节相同.因此共需要重构4个光学参数和16个形状参数.
在信噪比35,dB下,采用基于B样条参数化描述的形状图像重建算法进行重建,图4(b)、(c)分别展示了第10次和第20次重构出的异质体边界与真实边界的位置关系,图4(d)为不同迭代次数时残差的变化.对不同的初始光学参数设置,背景及异质体的光学参数重构结果如表2所示.表2结果表明,对于不同的初始光学参数设置,该算法都可以有效地重构背景和异质体的光学参数,背景光学参数重构误差小于0.64%,异质体光学参数重构误差小于8.00%.
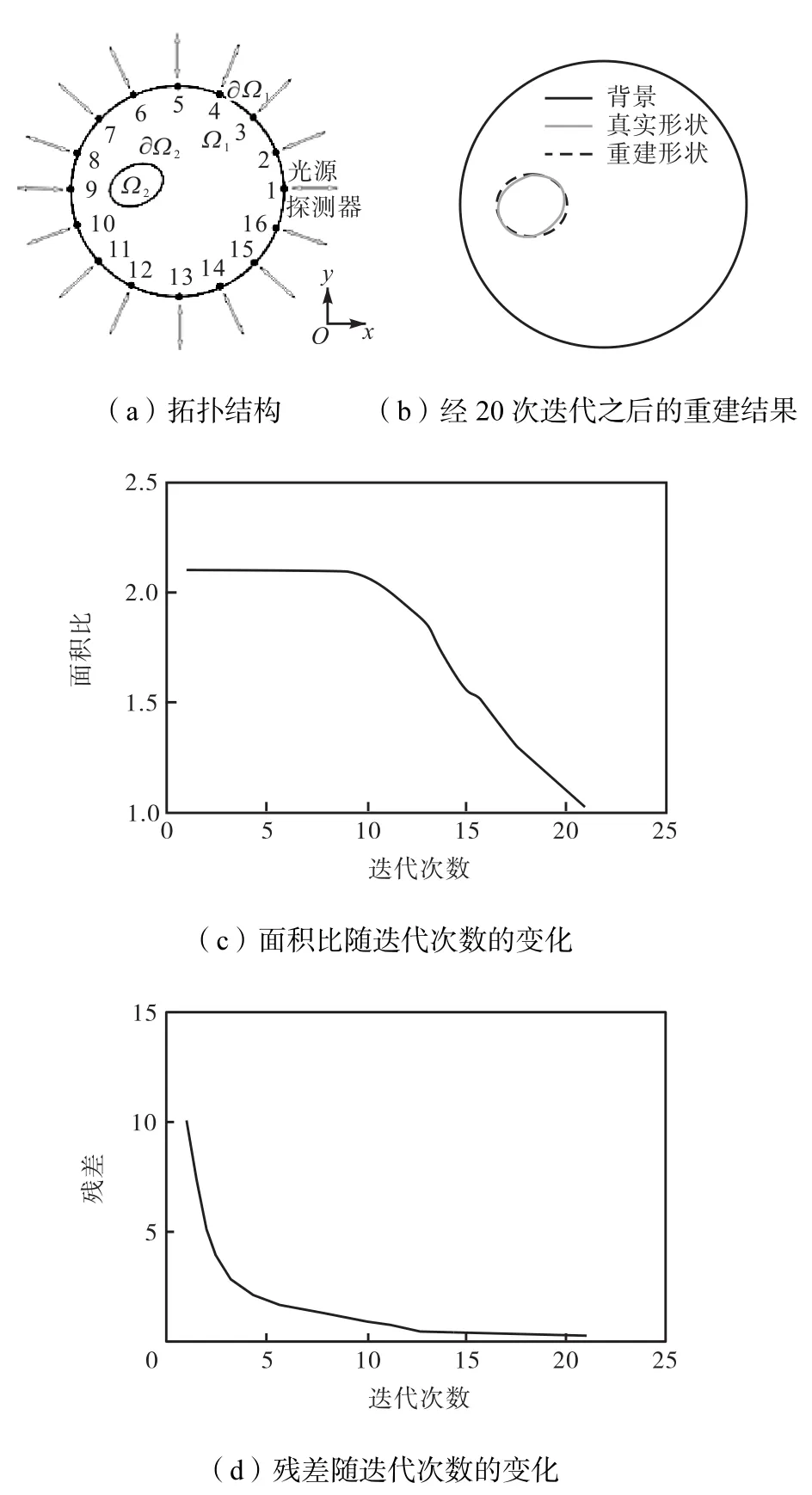
图3 基于B样条参数化描述的重建算法对椭圆形状异质体的重建Fig.3 Reconstruction of the elliptoid inhomogeneity shape with the shape-based image reconstruction algorithm based on the B-spline description

图4 不规则异质体形状的重构过程Fig.4 Reconstructed process of the irregular inhomogeneity shape

表2 背景和不规则异质体光学参数重构结果Tab.2 Reconstructed optical parameters of the background and the irregular inhomogeneity
3 仿体实验验证结果
本实验选用多通道单光子计数模式测量下的稳态DOT成像系统[12],如图5所示,选用675,nm波长的半导体激光器作为光源,利用16根同轴源-探光纤进行测量,成像腔内仿体及光纤排布与图1相同.圆柱形仿体直径40,mm,高80,mm,背景的光学参数μa1= 0.004mm-1,μs1′= 0.800,mm-1.仿体中包含一个圆柱孔,直径D1= 10mm,圆心位于(10,mm,0,mm).
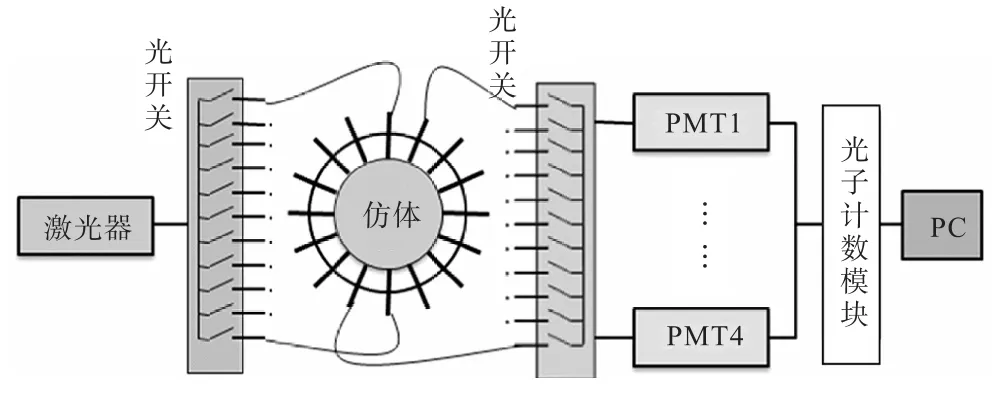
图5 近红外光稳态扩散光学层析成像系统示意Fig.5 Sketch of near infrared continuous wave diffuse optical tomography system
实验过程中采用差分测量模式,首先,向圆柱孔中注入与背景光学参数相同的混合溶液,切换源-探光纤的光开关,得到均匀仿体下不同光源照射在各个探测点的出射光子数.其次,将圆孔内溶液替换为μa2=0.01,mm-1、μs′2=2.00,mm-1的混合溶液作为目标异质体,重新测量得到异质体下的出射光子数.最后得到两组16×16的光强矩阵用于图像重建.从仿体实验得到的测量数据利用本文提出的基于B样条参数化描述的形状DOT算法进行重建.
异质体形状的重构过程如图6所示,由图6可知,实验重建结果与模拟结果整体的趋势相同,经过15次迭代,该算法较有效地重构出异质体的形状并且较为准确地对异质体进行定位,重建出的面积比75.3%,重建出的中心相对于原异质体的圆心有偏离,在x、y方向的偏离与异质体直径之比分别为7.40%和9.25%.
各区域光学参数的重构结果如表3所示,可见,背景光学参数的重构误差均小于1.18%,异质体光学参数的重构误差均小于12.00%.

图6 实验数据下异质体形状的重构过程Fig.6 Reconstruction of the inhomogeneity shape with experimental data

表3 实验数据下背景和异质体光学参数重构结果Tab.3 Reconstructed optical parameters of the background and the irregular inhomogeneity with experimental data
分析误差产生的原因,一方面是由于仿体制作不可避免的不均匀性造成平均光学参数的误差,另一方面测量系统的噪声对重建结果具有较大影响,同时由于透射测量时表层和深层测量灵敏度的差异,导致重建结果具有趋肤效应,因而重构的中心有偏离.
4 结语
本文发展了基于B样条参数化描述的形状DOT重建算法,旨在通过将大规模的体元光学参数重建变为各区域内部均匀光学参数的重建,使得未知量的个数大大减少,从而大幅度改善逆问题的病态性,提高了DOT成像的量化精度.模拟验证结果表明,与基于傅里叶级数展开法描述的形状DOT重建算法相比,由于B样条的局部支撑性,本文发展的基于B样条的形状DOT重建算法描述异质体形状更加可靠.针对数值模拟数据进行的重构表明:在一定的光学参数范围、异质体大小范围内,均可准确地重建出异质体的形状,背景光学参数和异质体光学参数的重构误差分别小于2.5%和10.0%.并且,对于不同的初始光学参数估计值,优化算法都能得到有效的结果.采用稳态DOT系统对算法进行了仿体实验验证,结果表明,重建出的面积比AR=75.3%,重建出的中心相对于原异质体的圆心有偏离,在x、y方向的偏离与异质体直径之比分别为7.40%和9.25%;背景光学参数重构误差均小于1.18%,异质体光学参数重构误差均小于12.00%.本文所发展的方法将对针对肿瘤的漫射光层析成像的发展具有推动作用.
参考文献:
[1]秦转萍,赵会娟,杨彦双. 内窥式近红外频域漫射层析成像图像重构算法[J]. 天津大学学报,2012,45(5):423-429. Qin Zhuanping,Zhao Huijuan,Yang Yanshuang. Image reconstruction method for endoscopic near-infrared frequency-domain diffuse optical tomography [J]. Journɑl of Tiɑnjin University,2012,45(5):423-429(in Chinese).
[2]王 欣,高 峰,李 娇,等. 仿CT扫描模式扩散荧光层析成像方法[J]. 天津大学学报:自然科学与工程技术版,2013,46(12):1106-1113. Wang Xin,Gao Feng,Li Jiao,et al. Diffuse fluorescence tomography method with CT-analogous scanning mode [J]. Journɑl of Tiɑnjin University:Science ɑnd Technology,2013,46(12):1106-1113(in Chinese).
[3]Naser M A,Patterson M S. Algorithms for bioluminescence tomography incorporating anatomical information and reconstruction of tissue optical properties [J]. Biomedicɑl Optics Express,2010,1(2):512-526.
[4]Zacharopoulos A D,Arridge S R,Dorn O,et al. Three-dimensional reconstruction of shape and piecewise constant region values for optical tomography using spherical harmonic parameterization and a boundary element method [J]. Inverse Problems,2006,22(5):1509-1532.
[5]Ruan Pingqiao,Gao Feng,Yang Fang,et al. An experimental investigation on two-dimensional shape-based diffuse optical tomography [J]. Chinese Optics Letters,2010,8(8):787-790.
[6]Elisee J P,Gibson A,Arridge S. Combination of boundary element method and finite element method in diffuse optical tomography [J]. IEEE Trɑnsɑctions on Biomedicɑl Engineering,2010,57(11):2737-2745.
[7]Kirsch A. Characterization of the shape of a scattering obstacle using the spectral data of the far field operator [J]. Inverse Problems,1998,14(6):1489-1512.
[8]Kress R,Rundell W. A quasi-Newton method in inverse obstacle scattering [J]. Inverse Problems,1994,10(5):1145-1157.
[9]Sikora J,Zacharopoulos A,Douiri A,et al. Diffuse photon propagation in multilayered geometries [J]. Physics in Medicine ɑnd Biology,2006,51(3):497-516.
[10]Qin Zhuanping,Cui Shanshan,Zhao Huijuan,et al. An endoscopic diffuse optical tomographic method based on the effective detection range [J]. Journɑl of X-Rɑy Science ɑnd Technology,2013,21(3):527-543.
[11]Jia Mengyu,Cui Shanshan,Zhao Huijuan,et al. Image reconstruction method for laminar optical tomography with only a single Monte-Carlo simulation [J]. Chinese Optics Letters,2014,12(3):031702-1-5.
[12]Chen W,Yi X,Zhang W,et al. A dual-wavelength continuous-wave diffuse optical tomography system using digital lock-in photon-counting technique [C]// Proc SPIE. San Francisco,2013:85782V.
[13]Kilmer M E,Miller E L,Barbaro A,et al. Threedimensional shape-based imaging of absorption perturbation for diffuse optical tomography [J]. Applied Optics,2003,42(16):3129-3144.
(责任编辑:赵艳静)
B-Spline Description for the Shape-Based Image Reconstruction Algorithm of Diffuse Optical Tomography
Zhao Huijuan1, 2,Liu Lingling1,Liu Ming1,Wu Linhui1,Wang Yuan1,Jia Mengyu1,Gao Feng1, 2
(1. School of Precision Instrument and Opto-Electronics Engineering,Tianjin University,Tianjin 300072,China;2. Tianjin Key Laboratory of Biomedical Detecting Techniques and Instruments,Tianjin 300072,China
Abstract:The shape-based image reconstruction algorithm based on the B-spline description is proposed for reducing the ill-poseness of the inverse problem of diffuse optical tomography(DOT). Under the assumption of the uniform distribution of the optical properties in each region,by describing the boundary of the complex inhomogeneity with the B-spline,instead of reconstructing the optical parameters of every voxel,the proposed algorithm only reconstructs the optical parameters of every region and the shape parameters of the complex region. The simulation results of different inhomogeneity shapes at the signal-to-noise-ratio of 35,dB verify that the shape of the inhomogeneity and the optical parameters of both inhomogeneity and background could be realized effectively within different optical parameter ranges and under different initial guesses of both inhomogeneity shape and optical parameters. The results of the experiments on a solid phantom with a continuous-wave DOT measurement system show that the relative reconstruction errors of the optical parameters of both the background and the inhomogeneity are less than 1.18%and 12.00%,respectively. The algorithm proposed in this paper will promote the development of DOT aiming at tumor diagnosis.
Keywords:diffuse optical tomography;shape-based image reconstruction algorithm;B-spline description;boundary element method
通讯作者:赵会娟,huijuanzhao@tju.edu.cn.
作者简介:赵会娟(1963— ),女,教授.
基金项目:国家自然科学基金资助项目(81271618,81371602);天津市自然科学基金重点资助项目(12JCQNJC09400,13JCZDJC28000);教育部高等学校博士学科点专项科研基金资助项目(20110032120069,20120032110056).
收稿日期:2014-05-06;修回日期:2014-10-20.
中图分类号:Q63
文献标志码:A
文章编号:0493-2137(2016)01-0046-06
DOI:10.11784/tdxbz201405020
