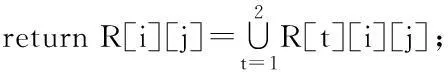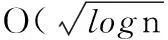基于RPC模型的访问控制策略压缩算法

程玉柱　易月娥

(长沙民政职业技术学院软件学院　湖南 长沙 410004)



基于RPC模型的访问控制策略压缩算法

程玉柱易月娥

(长沙民政职业技术学院软件学院湖南 长沙 410004)

摘要访问控制列表(ACL)提供了对网络设备接口的一种基本访问控制，是维护网络系统安全的重要手段之一。随着网络应用的日益增多，ACL条目也随之增加，使得管理ACL更加困难，降低了网络设备的转发性能。因此对ACL进行压缩显得尤为重要，但该问题已被证明是NP难。针对ACL压缩问题，提出基于矩阵映射和构建独立单元空间集的方法，将其转换为直线多边形的矩形覆盖问题。分析表明该问题的求解近似度可以突破O(logn)，为ACL压缩问题的求解提供了新的思路。

关键词访问控制列表网络安全规则压缩RPC矩形覆盖

AN ALGORITHM OF ACCESS CONTROL POLICY COMPRESSION BASED ON RPC MODEL

Cheng YuzhuYi Yuee

(Software Department,Changsha Social Work College,Changsha 410004,Hunan,China)

AbstractAccess control list (ACL) provides a basic access control on network device interfaces, and is one of the important means to maintain the security of network systems. However, ACL items have been growing along with the increase of network applications, while increasing the difficulty in ACL management, this also degrades the forwarding performance of network devices as well. Therefore to compress ACL is particularly important, but this problem has been proved to be NP-hard. Aiming at ACL compression problem, the paper proposes an approach based on mapping matrix and constructing independent unit space set to transform the problem into a problem of rectilinear polygon rectangle cover. Analysis shows that the approximation degree of the solution to the problem can break O (logn), this offers a new thought for solving ACL compression problem.

KeywordsACLNetwork securityRule compressionRectilinear polygon cover (RPC)Rectangle cover

0引言

随着人们对网络依赖程度的日益增强，网络安全性愈发重要，路由器作为网络传输过程中的重要设备，对报文安全、正确和快速的转发起着关键作用。在路由器上配置访问控制列表ACL[1]，通过访问规则控制和过滤经过路由器的数据流，防止外部用户对内部网络不安全的访问。访问控制列表由源地址、目的地址、端口号等一系列特定指示条件组成，其采用自上而下的执行顺序，当数据包到达时，路由器会遍历ACL内所有规则，直至找到第一条匹配数据包的规则，并执行该规则所定义的操作(拒绝或允许)。在高速网络环境中，会引入一种特殊的硬件机制(TCAMs)[2]来对遍历并行处理以加快数据包转发速度，但TCAM内存受限且价格昂贵，因此需要考虑如何尽可能地压缩ACL内规则条数以优化TCAM的存储结构[3]。此外，当ACL内规则条数达到一定数量时，对ACL进行编辑和管理会变得非常繁琐而且容易出错，甚至由此带来灾难性的后果[6]。因此，有必要在保持ACL语义不变的前提下，对ACL进行尽可能的压缩。不失一般性，本文研究只包含源地址和目标地址的二维ACL压缩问题。

1理论基础

一般而言，ACL内任意规则可以表示为形如“F1∈D(F1)(F2∈D(F2)→decision”的形式，这里Fi(1≤i≤2)分别表示源地址和目标地址，D(Fi)表示对应的域值区间，decision表示规则的决策(接受或拒绝)。根据文献[8]中规则空间的定义，可进一步将ACL规则表示为R[(l1,l2)(d1,d2):0] (如果 =discard)) 或者R[(l1,l2)(d1,d2):1] (如果 =accept), 这里 li是 D(Fi)的下界，而di代表D(Fi)的大小。下面正式给出本文算法所涉及的一些概念定义。

定义1针对域(F1,F2)的映射矩阵M2满足以下几点要求：

(1) M2是一个二维矩阵，各维坐标用Fi表示，相应坐标区间为[0, D(Fi)], 1≤i≤2。

(2) M2由一系列单元矩阵组成，每个单元矩阵可用其下界坐标及相应坐标区间表示:[(l1,l2)(d1,d2)]。

(3) 任一具有形如→的ACL规则可在M2中表示，即每一条规则的前缀可以用M2中的一个单元矩阵来表示，而单元矩阵的值则可以用来表示规则的决策:value=0 (如 =discard ),或value =1 (如=accept)。

(4) 一个包含有m个互为独立的单元矩阵的二维矩阵M2可以形式化描述为:

这m个独立单元矩阵在M2内互不相交，我们把这些独立单元矩阵称作单元空间。

定理1任意原始ACL规则，采用FDM构建算法[8]，在矩阵M2内按逆序依次映射后，可得到一串语义与原始ACL规则完全相同的单元空间。

证明：因为ACL规则遵循首次匹配优先原则，即数据包会执行最先匹配规则的决策。根据算法过程，原始规则按逆序逐条映射到二维矩阵之中，并根据规则各维域值范围及对应决策对相应单元空间进行赋值。因为自后而前的映射过程保证了规则的首次优先匹配，同时单元空间与规则域值范围保证了完全一致。因此，可知原始ACL规则采用FDM构建算法在二维矩阵内映射后，规则语义保持不变。得证。

定理2任意两个单元空间Ui和Uj在某一个维度上的坐标关系R(Ui,Uj)=r有且只属于{左相邻、右相邻、左相交、右相交、分离、覆盖、包含、相等}之一，分别表示为{╜,╙ ,┤,├,║,>,<,≡}。本定理证明略。

我们定义两个单元空间的空间关系为各个维度上的坐标关系的组合。当两个单元空间的空间关系中，有一个“║”或者同时有两个“╜或╙”，则定义对应的两个单元空间的空间关系为“分离”。我们可以把任一单元空间看作无向连通图中的一个点，两单元空间不互为分离则表示其对应图中的两点之间有边相连，类似求独立连通子图，我们把映射后得到的单元空间划分为若干独立的单元空间集。每个独立单元空间集正好可以构成一个二维直线多边形，由定义1可知多边形内各单元空间的值均为1，若几个单元空间围成一个圈，而圈内区域值为0，则把这些值为0的区域称作“洞”[4]。

2基于RPC问题模型的ACL压缩算法

我们首先用FDM构建算法[8]将原始ACL规则映射成一系列单元空间，然后基于各单元空间的空间关系将它们划分为若干独立单元空间集，每个独立单元空间集正好可以构成一个直线多边形。从几何学观点看，此时ACL压缩问题等价于如何用最少的矩形去覆盖该直线多边形，即RPC问题。下面，我们举一个例子来详细说明方法步骤。设原始ACL包含9条规则，如图1所示。

图1　原始ACL规则示例

步骤1将ACL规则映射到二维矩阵M2

将规则ri映射到二维矩阵M2的详细算法可参考文献[8]，图2为该算法过程示例。设有两条规则r1: F1∈[4,5]∧F2∈[4,6]→discard, r2: F1∈[1,7]∧F2∈[2,8]→accept，图2(a)为规则r2映射后的结果。这里(1,r2)表示规则r2的决策为接受，类似地，图2(b)内(0,r1)表示规则r1的决策为拒绝。因为r1的决策是拒绝且r1的规则空间被包含在r2映射后的单元空间内，首先将单元空间 [(1,2)(7,7)]在F1维上切分成三部分，{[(1,2)(3,7)], [(4,2)(2,7)], [(6,2)(2,7)]}，而在F2维上保持不变，然后继续将 [(4,2)(2,7)]在F2维上进行切分为三部分:{[(4,2)(2,2)], [(4,4)(2,3)], [(4,7)(2,2)]}，因为[(4,4)(2,3)]与r1的规则空间一样，将其移除，从而得到最终的四个单元空间{[(1,2)(3,7)],[(4,2)(2,2)], [(4,7)(2,2)], [(6,2)(2,7)]}。

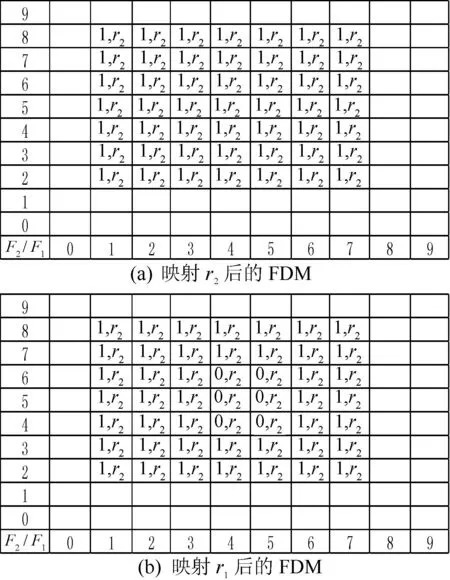
图2　映射示例:r1:F1∈[4,5]∧F2∈[4,6]→discard, r2: F1∈[1,7]∧F2∈[2,8] →accept

以图1所示的原始ACL为输入，通过映射过程，可以得到六个单元空间格，最后的FDM为{[(0,4)(3,4)],[(2,2)(1,2)],[(3,2)(1,3)],[(5,5)(2,3)],[(7,2)(2,8)],[(9,5) (1,3)]}，如图3所示。

图3　规则映射后结果示例

步骤2求独立子集

该方法第一步需要判断任意两单元空间之间的空间关系(具体判定过程见算法1)，可得到对应的空间关系矩阵M，图4展示了图3各单元空间之间的空间关系矩阵。对M内每一个矩阵元素，当存在一个“║”或有两个“╜或╙”时，对应的两单元空间可以定义为“分离”。我们把任一单元空间看作无向连通图中的一个点，两单元空间不互为分离则表示其对应图中的两点之间有边相连，类似求独立连通子图方法[12]，可以容易地求得独立单元空间集S1和S2：

S1={[(0,4)(3,4)],[(2,2)(1,2)],[(3,2)(2,3)]}

S2={[(5,5)(2,3)],[(7,2)(2,8)],[(9,5)(1,3)]}

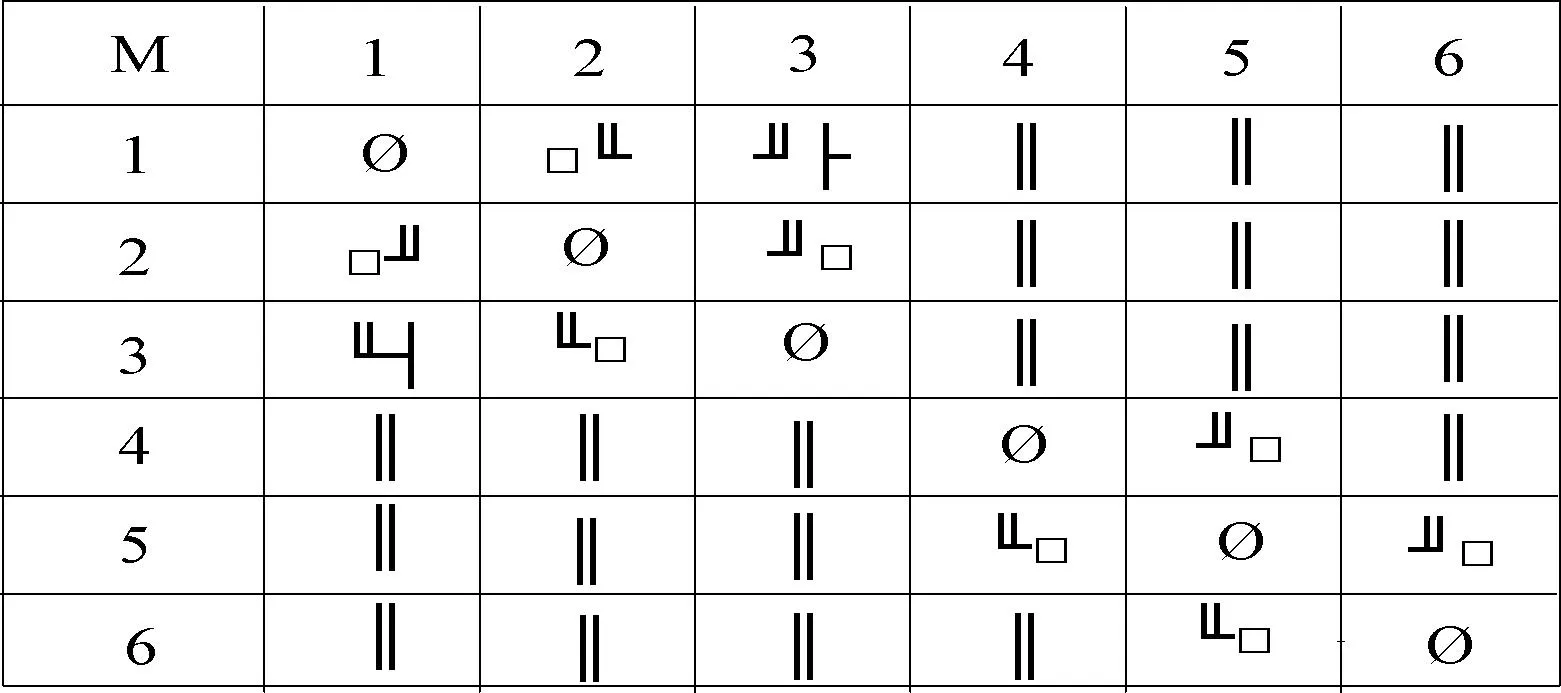
图4　空间关系矩阵示例

算法1构建空间关系矩阵

输入:包含n个单元空间的单元空间集UNs

输出:空间关系矩阵M，矩阵元素为任意两单元空间的空间关系

Begin

Steps:

1. 对单元空间集坐标递增顺序进行排序(U1~ Un);

2. for i:=1 to n

for j:=1 to n do

if i==j then do M[i][j]=∅;

else do M[i][j]=Relation(Ui,Uj);

End

Relation(Ui,Uj){

/*设Ui=(l1(i),l2(i))(d1(i),d2(i)),Uj=(l1(j),l2(j))(d1(j),d2(j)), t代表维度，在任一维，如Ui坐标小于Uj, 且两者相邻或相交，则称两单元空间在该维度上为左相邻或左相交。反之类似定义*/

for t:=1 to 2 do

if (lt(i)+dt(i)lt(j)+dt(j)) then R[t][i][j]=║;

if (lt(i)+dt(i)=lt(j)‖lt(i)=lt(j)+dt(j))

then R[t][i][j]=╜‖R[t][i][j]=╙;

if (lt(i)

then R[t][i][j]=┤‖├;

if (lt(j)

then R[t][i][j]=<‖> ;

if (lt(i)=lt(j)&dt(i)=dt(j)) then R[t][i][j]=≡;

} // End of Relation(Ui,Uj)

步骤3直线多边形的矩形覆盖

每个独立单元空间集正好可以构成一个直线多边形，从几何学观点看，此时ACL压缩问题等价于RPC问题。考虑一般情况，该直线多边形可能含有“洞”。

根据算法2，对独立子集S1和S2分别进行处理，得覆盖S1的矩形{[(0,4)(3,4)],[(2,2)(2,3)]},覆盖S2的矩形{[(5,5)(5,3)],[(7,2)(2,8)]}。最后根据文献[8]内的规则生成算法，可得压缩后的ACL规则为：

r1:F1∈[7,8]∧F2∈[2,9]→accept

r2:F1∈[5,9]∧F2∈[5,7]→accept

r3:F1∈[0,2]∧F2∈[4,7]→accept

r4:F1∈[2,3]∧F2∈[2,4]→accept

r5:F1∈[0,9]∧F2∈[0,9]→discard

算法2Covering Rectilinear Polygons with Rectangles

Input: A 2-dimensional rectilinear polygon P with n vertices

Output: m rectangles which can cover the whole P

Begin

Steps:

1. A sequence of consecutive vertically aligned non-hole cells bounded by a hole on the top and the bottom constitutes a strip;

2. For each strip, put the unique associated rectangle whose height just covers the strip and whose width is as large as possible;

End

3理论分析与仿真结果

定理3两个在空间上互为独立的单元空间，其所对应的规则集也互为独立。即求整个单元空间的最少矩形覆盖等价于求各独立单元空间集的最少矩形覆盖的组合。

证明：采用反证法，设两个独立的单元空间集，所对应的规则集不互为独立，即存在两条规则(记为ra和rb)分别属于不同的单元空间集，但两规则互为包含或者相交，即等价于存在某个区间，同时属于ra和rb，但根据我们的FDM构建算法，此即意味着存在某个单元空间，同时属于两个不同的单元空间集，这与两单元空间集互为独立相矛盾。得证。

定理4二维ACL规则通过矩阵映射[8]后的压缩问题求解近似度可以突破O(logn)。

1) 基于各单元空间相互之间的空间关系，可以将全部的单元空间划分到各独立单元空间子集。

2) 各单元空间子集内值为1的单元空间通过邻接关系连在一起，可以构成一个多边形，该多边形内部可能有值为0的单元空间，其可以看作多边形的洞。

3) 如果能用最少的矩形覆盖该多边形，即相当于对这些单元空间进行最大程度地压缩，问题模型与RPC相同。故得证。

实验分别选取实际ACL规则和合成规则进行测试，我们选取了一个53条规则的实际ACL，此外用Classbench[13]自动生成了十个合成规则，规则条数分别从14至200条。任意ACL规则前缀均有且只包含源和目标IP地址两个域。采用文献[8]中的FDM方法和本文提出的RPC方法分别对各规则进行压缩，得到的压缩结果如图5所示。

图5　RPC与FDM方法压缩比较

可以看到，RPC方法相比FDM方法而言，在压缩率上更优，这个结果不难理解，因为FDM方法相当于图6(a)所示的MNC问题(Minimal Nonoverlapping Cover)而RPC方法相当于图6(b)所示的MOC(Minimal Overlapping Cover)问题[11]。

图6　直线多边形的矩形覆盖示意图

4结语

随着网络的飞速发展，ACL在网络安全、网络优化等方面得到越来越多的应用。但二维及以上的区间ACL压缩问题已被证明是NP难。本文基于矩阵映射方法基础，提出将ACL压缩问题转化成RPC问题，突破了目前已知的最好近似度O(min(n1/3,OPT1/2))。仿真实验表明其比传统ACL压缩方法具有更高的压缩比。下一步工作研究如何将该方法应用到多维防火墙规则压缩之上。

参考文献

[1] 曾旷怡,杨家海.访问控制列表的优化问题[J].软件学报,2007,18(4):978-986.

[2] Rottenstreich O,Cohen R,Raz D,et al.Exact worst case TCAM rule expansion[J].IEEE Transactions on Computers,2013,62(6):1127-1140.

[3] Meiners C R,Liu A X,Torng E.Bit Weaving:A non-prefix approach to compressing packet classifiers in TCAMs[J].IEEE Trans on Networking,2012,20(2):488-500.

[4] Applegate D A,Calinescu G,Johnson D S,et al.Compressing rectilinear pictures and minimizing access control lists[C]//Proc.of the eighteenth annual ACM-SIAM symposium on Discrete algorithms,2007:1066-1075.

[5] Suri S,Sandholm T,Warkhede P.Compressing two-dimensional routing tables[J].Algorithmica,2003,35(4):287-300.

[6] Liu A X,Torng E,Meiners C.Firewall Compressor:An algorithm for minimizing firewall policies[C]//Proc.of the IEEE INFOCOM,April 2008.Phoenix,AZ,2008:176-180.

[7] Daly J,Liu A X,Torng E.A difference resolution approach to compressing access control lists[C]//Proc.of the IEEE INFOCOM,April 2013:2040-2048.

[8] Cheng Y,Wang W,Min G,et al.A new approach to designing firewall based on multidimensional matrix[J].Concurrency and Computation:Practice and Experience,2013,11(27):1-14.

[9] Hu H,Ahn G J,Kulkarni K.Detecting and resolving firewall policy anomalies[J].IEEE Transactions on Dependable and Secure Computing,2012,9(3):318-331.

[10] O’rourke J,Supowit K.Some NP-hard polygon decomposition problems[J].IEEE Transactions on Information Theory,1983,29(2):181-190.

[11] Anil Kumar V S,Ramesh H.Covering rectilinear polygons with axis-parallel rectangles[C]//Proc.of the thirty-first annual ACM symposium on Theory of computing.ACM,1999:445-454.

[12] Richard M K,Avi W.A fast parallel algorithm for the maximal independent set problem[J].Journal of the Association for Computing Machinery,1985,32(4):762-773.

[13] Taylor D E,Turner J S.ClassBench:A packet classification benchmark[J].IEEE Transactions on Networking,2007,15(3):499-511.

中图分类号TP393.08

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.02.077

收稿日期：2014-05-08。湖南省教育厅科技项目(13C1049)。程玉柱，讲师，主研领域：网络信息安全。易月娥，副教授。