利用导数构造函数证明不等式
2016-03-17河北乐亭第一中学邵敬毅
河北乐亭第一中学 邵敬毅
利用导数构造函数证明不等式
河北乐亭第一中学 邵敬毅
导致 不等式 构造函数
不等式的证明有多种方法,以下是我在学习导数时掌握的一种证明不等式的新方法——构造函数法.应用这种方法证明不等式需要仔细观察定义域,找准关系,看清条件,分析特征,利用导数判断函数单调性求最值、极值等.该类题目可以考查我们对于函数知识的灵活运用能力,可谓全面而细致,巧妙而成形.
一、构造函数F(x)=f(x)-g(x),证明F(x)≥0
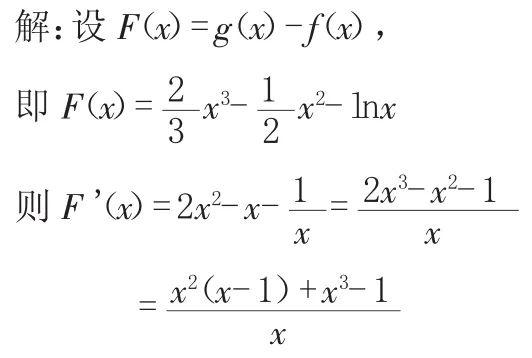
当 x∈(1,+∞)时,F'(x)>0,函数F(x)在(1,+∞)上单调递增.
∴g(x)>f(x).
∴在(1,+∞)上,f(x)的图像在g(x)的图像下方.
解题心得:要证明F(x)≥0,可通过构造函数F(x)=g(x)-f(x),从而将不等式证明问题转化为函数的最值问题,通过证明[F(x)]最小值≥0,使问题得以解决.
二、作差后局部构造函数
(1)求l的方程;
(2)证明:除切点(1,0)外,曲线C在直线l的下方.
∴直线l的方程为y=x-1.
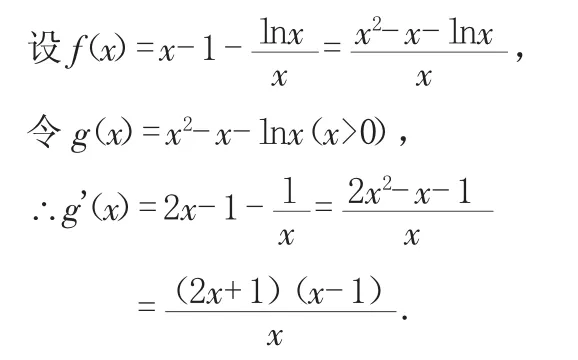
∴当0 当x>1时,g'(x)>0,g(x)单调递增. ∴当x=1时,g(x)有最小值g(1)=0, ∴g(x)≥0(当且仅当x=1时取等号). ∴除切点(1,0)外,曲线C在直线l的下方. 解题心得:通过局部构造函数,可以使复杂问题简单化,步步为营,各个击破,最终使问题得以解决. 例3已知函数f(x)=x-(x+1)ln(x+1) 求:(1)f(x)的单调区间; (2)证明:当n>m>0时,(1+n)m<(1+m)n. 解:(1)f'(x) 令f'(x)>0得:-1 令f'(x)<0得:x>0, ∴f(x)的单调递增区间为(-1,0),单调递减区间为(0,+∞). (2)要证(1+n)m<(1+m)n, 由(1)知: f(x)在(0,+∞)上单调递减, ∴当x>0时,f(x) 即:x-(1+x)ln(1+x)<0. ∴g(x)在(0,+∞)上单调递减. ∵n>m>0, ∴g(n) 从而有:(1+n)m<(1+m)n. 解题心得:通过对要证不等式(1+n)m<(1+m)n的分析,通过两边取对数,可以使表达式的函数特征更加明显,从而实现从不等式证明到判断函数单调性的转化. 例 4 已知f(x)是定义在(0,+∞)上的非负可导函数,且满足xf'(x)+f(x)≤0.对任意正数a,b,若a A.af(b)≤bf(a) B.bf(a)≤af(b) C.af(a)≤bf(b) D.bf(b)≤af(a) 解:xf'(x)+f(x)≤0圯[xf(x)]'≤0, ∴ 函数F(x)=xf(x)在(0,+∞)上为常函数或单调递减. 又∵0 ∴af(a)≥bf(b)>0,① ∴af(b)≤bf(a),故选A. 解题心得:由函数在某区间导数值的正负判断可判断原函数在该区间的单调性,由此可联想到[xf(x)]'=xf'(x)+f(x),使问题得到初步的解决,此外,本题还综合考查了不等式的性质.三、取对数后构造函数
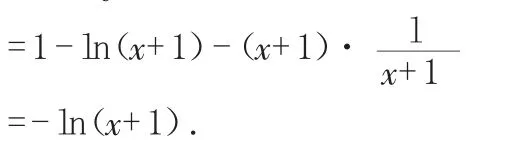

四、从条件特征入手构造函数证明
