异步电动机矢量控制解耦算法的研究

2016-03-16贾文哲王剑平

安徽农业科学 2016年3期

关键词：矢量控制

贾文哲，王剑平

(昆明理工大学信息工程与自动化学院，云南昆明 650500)

异步电动机矢量控制解耦算法的研究

贾文哲，王剑平*

(昆明理工大学信息工程与自动化学院，云南昆明 650500)

摘要由于异步电机的数学模型是非线性强耦合的，在进行异步电机矢量控制的时候，参数的解耦成为矢量控制的关键，不同的解耦策略将直接影响到异步电机矢量控制的品质。提出通过坐标变换后，观测两相坐标系的电流，通过电压方程计算得到解耦电压，将控制电压引入解耦电压并相加，共同作用在电机上，发现转子磁链的变换对转矩、转速的变换影响很小，可知解耦效果良好。

关键词异步电动机；强耦合；解耦；矢量控制

Research of Vector Control Decoupling Algorithm of Asynchronous Motor

JIA Wen-zhe, WANG Jian-ping*(College of Information Engineering and Automation, Kunming University of Science and Technology, Kunming, Yunnan 650500)

Abstract Since the mathematical model of asynchronous motor is a nonlinear strong coupling, parameters decoupling is the key of vector control during asynchronous motor vector control. Different decoupling strategies directly affect the quality of asynchronous machine vector control. In this research, the electric current of two coordinate systems was observed through coordinate transformation. Decoupling voltage was calculated by voltage equations. Control voltage was introduced into decoupling voltage, and then they worked together on the motor. It was found that the torque of rotor flux and the speed transformation had little effects; but the decoupling effects were good.

Key words Asynchronous motor; Strong coupling; Decoupling; Vector control

矢量控制中的重要问题就是磁场定向，磁场定向可以分为直接磁场定向和间接磁场定向，前者称为直接矢量控制，后者称为间接矢量控制。直接矢量控制是通过磁场检测或运算来确定转子磁链矢量的空间位置，控制方法简单，但是受外界和自身干扰性大；间接矢量控制是通过控制转差频率来实现的。

按照转子磁场定向矢量控制系统，构建感应电机数学模型，可以实现将定子电流分解为励磁分量ism和转矩分量ist，转子磁链ψr仅由定子电流励磁分量ism产生，而电磁转矩Te正比于转子磁链和定子电流转矩分量的乘积，实现了定子电流2个分量的解耦，为实现高性能调速提供了可能。但是从两相旋转坐标系下的状态方程来看，m轴和t轴的电流、磁链，还有同步转速之间仍然存在耦合，不利于动态性能的提高。对此，一种解决方法就是由观测模型得到m轴、t轴的电流后，计算得到解耦电压并与控制器输出电压相加后共同作用于电机，若观测模型足够精确且实时性很高，那么这种方法就是可行的[1]。笔者在此采用此方法进行分析研究。

1两相旋转坐标系异步电机数学模型

给出m、t坐标系下的异步电机，解耦后数学模型如下[2-4]：

(1)

在式(1)中，以m轴为例说明，式子前2项是直接对m轴电流产生控制作用的控制电压，第3项是t轴电流在m轴上产生的耦合电压，这部分电压需要控制系统给出相应的补偿，用以消除两轴之间电压电流存在的耦合关系，以达到和他励直流电机一样的控制效果[5-7]。解耦以后的状态方程如下所示。

(1) 磁链状态方程：

(2)

(3)

(2)转速状态方程:

(4)

(5)

由式(2)~(5)进一步推导，可得m、t轴的电流和输入电压的传递函数：

(6)

(7)

2数字控制器设计

给出异步电机相应参数如下：rs=2.2Ω,rr=1.09Ω,Ls=Lr=0.017 5H,Lm=0.602H。

2.1磁链子系统电流环设计受控对象为：

(8)

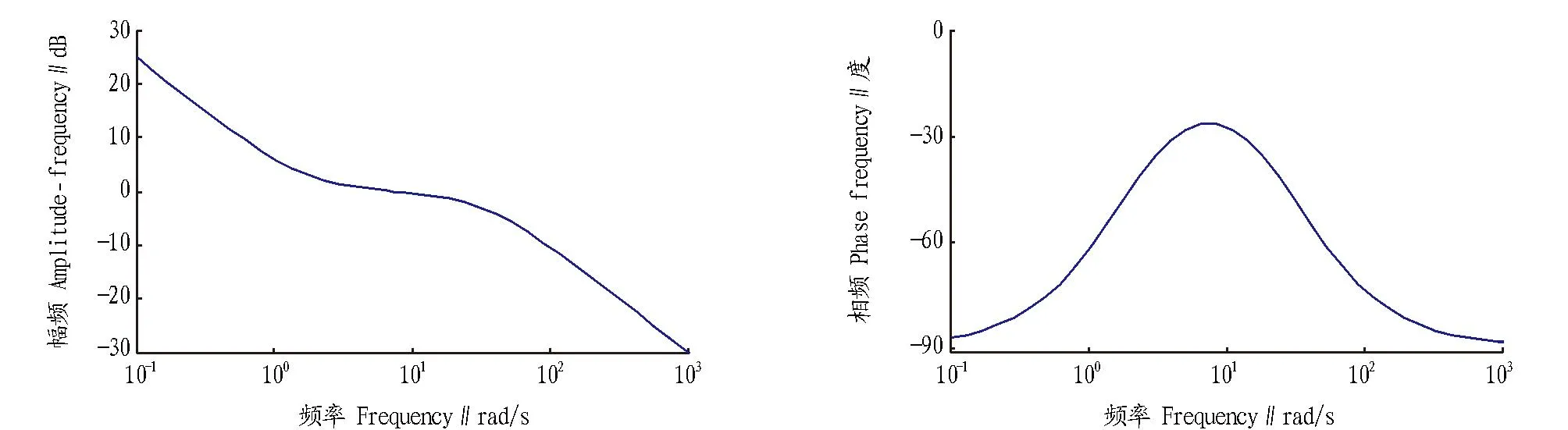
图1　系统开环Bode图Fig. 1　The diagram of system open-loop Bode

其Bode图如图1所示。从系统开环Bode图可以看出，开环剪切频率ωc=0.764rad/s,取ωs≥6~10ωc,T=0.013s。

可以看到，在高频段和低频段系统的幅频特性以-20 db每10倍频程衰减，在中频段接近于0，所以考虑先加入一个积分环节，然后再抵消分母中时间常数较大的那项，最后进行零极点配置以确定转折频率，使系统具有足够带宽，最终得到的调节器形式为：

(9)

校正后的开环传递函数为:

(10)

其Bode图如图2所示。采用双线性变换得到Dd(z)为：

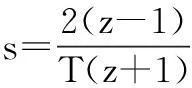
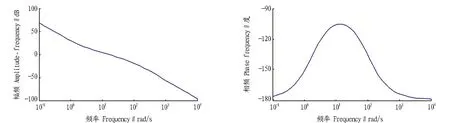
图2系统校正后的Bode图Fig. 2　Bode diagram of system after adjustment

(11)2.2转速电流环调节器设计转速子系统电流环调节器传递函数如下：

(12)

其Bode图如图3所示。剪切频率趋于零，可以认为对采样周期无影响，幅频响应先为0后-20dB衰减，所以为了保证相应的快速性，并且剪切频率与上述磁链子系统一致，可以将其校正为纯积分环节，此时调节器形式如下：

(13)

校正后的开环传递函数为：

(14)

校正后的Bode图如图4所示。采用双线性变换得到Dq(z)为:

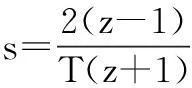
(15)

3仿真试验

根据以上推导可以建立如下仿真模型，其中速度外环的控制器采用MATLAB中的离散PID，并加入限幅，经过调试选择kp=5，ki=2，kd=0。MTLAB仿真图如图5所示。

仿真条件设置为：仿真时间30 s，磁链给定为初始值0.805 6，20 s后阶跃到0.5，转速给定为初始值100, 9 s后阶跃到300，负载转矩给定为初始值0，空载启动，6 s后阶跃到5。仿真结果如图6~8所示。

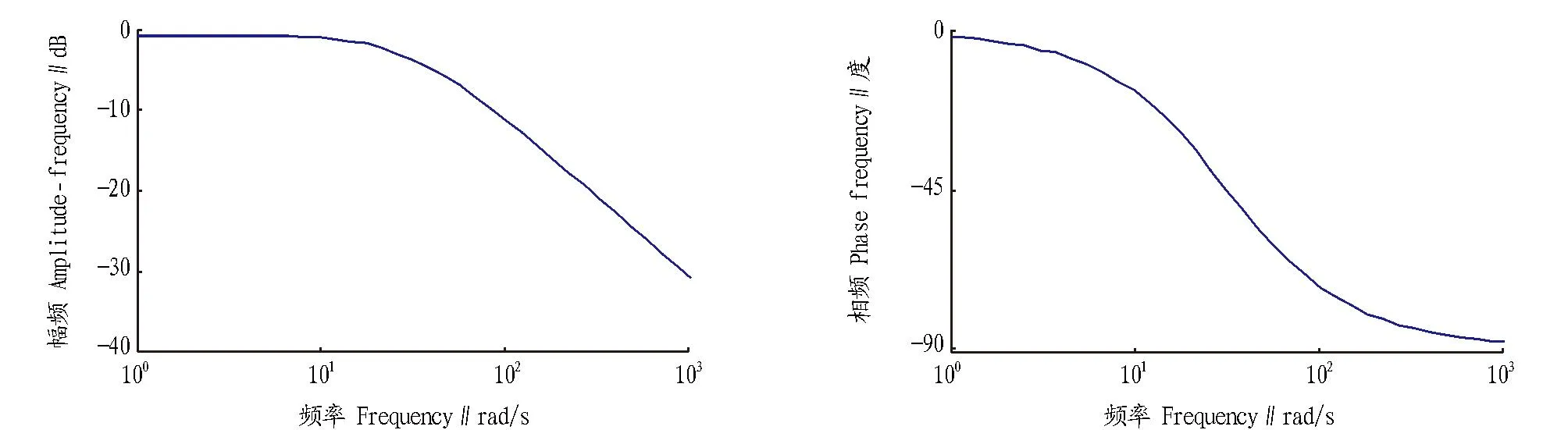
图3　电流环Bode图Fig. 3　Diagram of current loop Bode

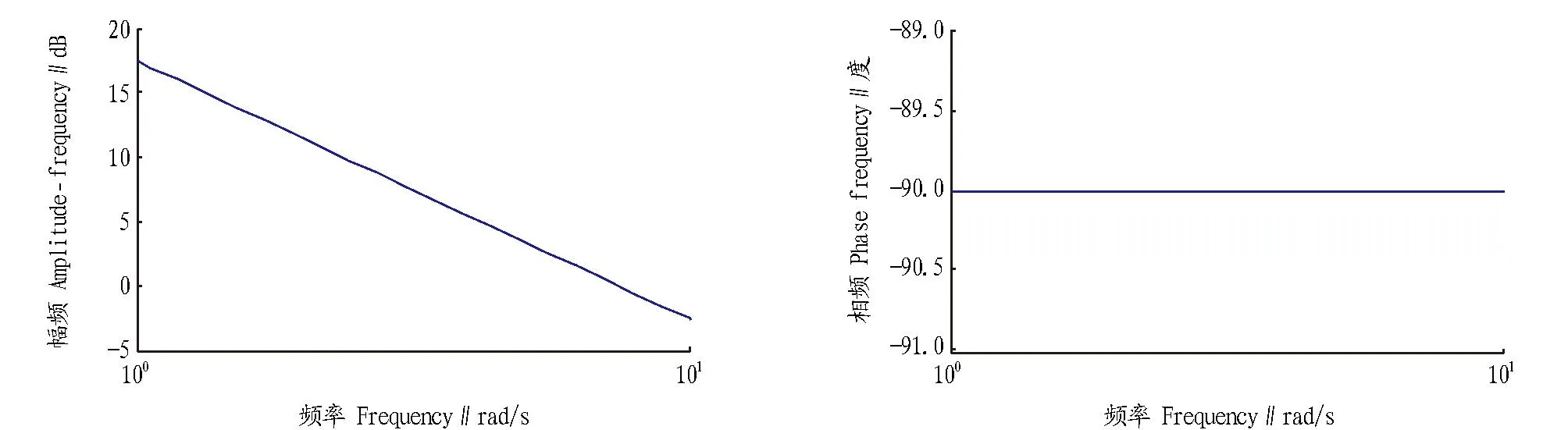
图4　电流环校正后Bode图Fig. 4　Bode diagram of current loop after correction

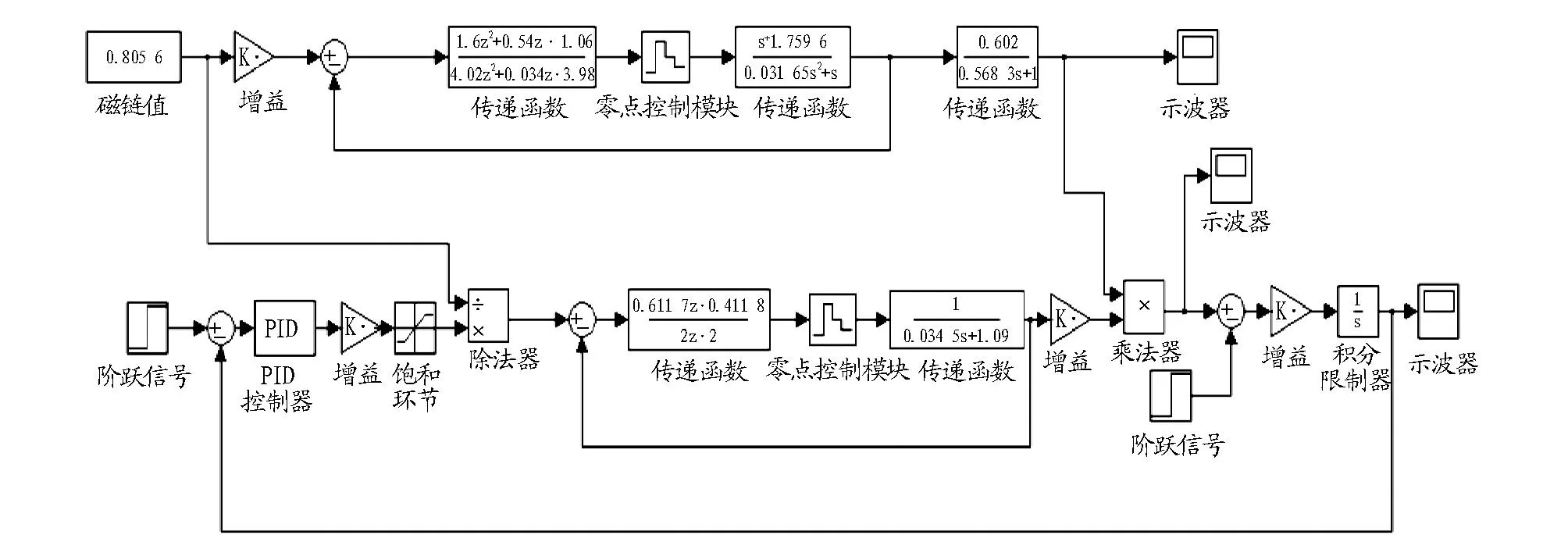
图5　MATLAB仿真图Fig. 5　Diagram of MATLAB simulation

从仿真结果可以看到，系统响应速度较快，转速稳态无静差，而且磁链变化对转速和转矩的影响较小，基本解耦，缺点是转速、转矩超调量较大，还需要进一步修改3个调节器的参数。

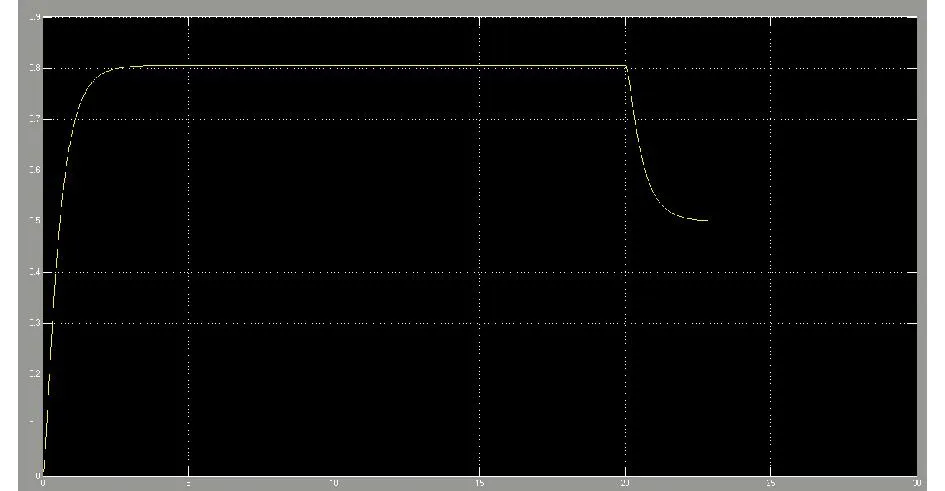
图6　仿真试验磁链波形Fig. 6　Flux waveforms in simulated test

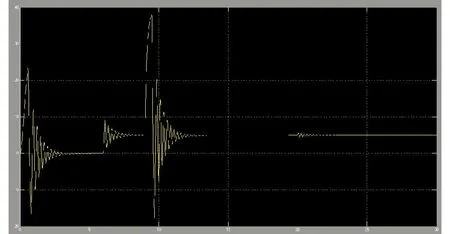
图7　仿真试验转矩波形Fig. 7　Torque waveform in simulated test

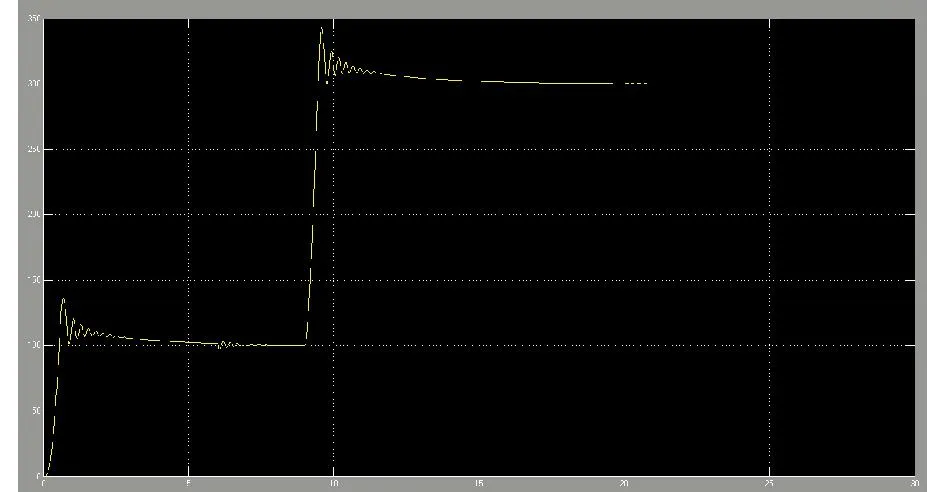
图8　仿真试验转速波形Fig. 8　Speed waveform in simulated test

4结语

该研究主要针对异步电机在进行矢量控制的时候，出现的非线性和强耦合的问题给出了一种解耦策略，基本采用的思想是设计了一种数字控制器，建立数学模型，通过数学分离的手段进行解耦，这种方法的优点在于解除了按转子磁链定向后，转子磁链与转速之间的耦合现象，实现了高性能调速，但是由于电机在运行中会受到外界环境的影响，导致电机参数发生变化，会降低控制品质与精度。

对于以后的研究重点在于引入新的智能算法，这种算法可以有较强的适应能力与跟踪性，对电机参数的依赖性较小，在低高速时能有较好的动态响应能力，这样变换大大改善异步电机的使用性能。

参考文献

[1] 周渊深.异步电动机解耦控制策略综述[J].中小型电机，2005,32(6)：56-60.

[2] 周志刚．一种感应电机的解耦控制方法[J]．中国电机工程学报，2003,23(2)：121-125．

[3] 沈滢，郝荣泰.感应电机矢量控制解耦算法的研究[J].北方交通大学学报，2003,27(2)：54-57.

[4] 苏宏志，高文华.交流异步电机电压解耦矢量控制系统的研究[J].现代电力，2005,22(3)：33-36.

[5] 陈栋,徐国卿,徐铁柱.一种基于DSP的交流电机矢量控制系统[J].电力系统及其自动化学报,2003,15(6):19-21, 36.

[6] 阮毅，陈伯时.电机拖动自动控制系统[M].北京:机械工业出版社，2009:183-190.

[7] 王成元，夏加宽，孙宜标.现代电机控制技术[M].北京:机械工业出版社，2013:69-80.

收稿日期2015-12-21

作者简介贾文哲(1990- )，男，黑龙江齐齐哈尔人，硕士研究生，研究方向：运动控制。*通讯作者，副教授，博士，从事运动控制、大数据等研究。

基金项目国家自然科学基金项目(61364008)；云南省应用基础研究重点项目(2014FA029)；云南省教育厅重点基金项目(2013Z127)；昆明理工大学复杂工业控制学科方向团队建设计划。