一种基于惯性/视觉信息融合的无人机自主着陆导航算法

刘 畅，杨良军,刘 峰，王 翌，徐 策，刘崇亮

(1.北京自动化控制设备研究所，北京 100074;2. 海军驻昆明地区军事代表处，昆明 650000)

一种基于惯性/视觉信息融合的无人机自主着陆导航算法

刘 畅1，杨良军2,刘 峰1，王 翌1，徐 策1，刘崇亮1

(1.北京自动化控制设备研究所，北京 100074;2. 海军驻昆明地区军事代表处，昆明 650000)

无人机自主着陆过程中需要实时获得高精度的导航信息，对自主性、实时性的要求较高。现有的导航方式都存在各自的不足，且在室内等新型环境中不能使用。针对这一问题，提出了一种视觉/惯性组合导航算法。首先建立了世界坐标系下惯性导航的数学模型，随后通过Kalman滤波实现位置、姿态匹配，其中位置匹配完成速度误差、加表零偏的估计；姿态匹配完成安装误差角、陀螺漂移的估计，并利用估计得到的安装误差角和视觉导航系统输出的姿态信息对惯导姿态进行修正。仿真结果表明，该算法具有一定的工程应用价值。

无人机；自主着陆；视觉/惯性组合导航；位置、姿态匹配

0 引言

无人机(Unmanned Aerial Vehicle,UAV)是一种无人驾驶、可重复使用的航空器的简称[1]，因其具有成本低、机动性能好、使用方便、无人员伤亡风险等众多优点，目前发展迅速，已经获得了广泛应用。自主飞行、执行任务是无人机新的发展方向，而自主着陆是其中的一个重要部分。

现有的着陆导航方式主要包括仪表着陆系统(ILS)[2]、微波着陆系统(MLS)[3-4]、DGPS/捷联惯导组合导航系统[5]，它们都有各自的不足：ILS轨道单一，下滑道固定，波束覆盖区很小，不能为飞机提供正常曲线进场和分段进场的信息，而且易受到在相近频率工作的无线电台、机场附近高层建筑甚至周围农作物的干扰，导致航向信标的失真；MLS 在性能上虽优于 ILS，但其设备昂贵，不利于推广，且这些设备机动性能较差，临时架设困难，不利于紧急行动；DGPS/捷联惯导组合导航系统存在卫星信号容易受干扰、室内无法定位等问题。此外，这三种导航系统都依赖外界信息的输入，容易受到干扰。因此研究出一种新的完全自主的、可靠的导航方式成为了解决无人机自主着陆问题的关键。

计算机视觉是用计算机实现人的视觉功能——对客观世界的三维场景的感知、识别和理解[6]。视觉导航系统[7-8]具有众多优点，一方面其结构简单、功耗低、信息量大，提升了无人机导航过程中的抗干扰能力和自主化程度；另一方面视觉导航精度较高，姿态精度可达角分级，定位可达到优于D‰的精度(D为无人机与着陆目标的相对距离)。因此利用计算机视觉信息来辅助完成或独立完成无人机的自主着陆任务已成为新的发展趋势。然而一些情况也会导致视觉导航系统无法正常工作，如当无人直升机降至一定高度时，摄像头视野范围内可能只包含一部分着陆目标；或着陆目标被建筑物等障碍物遮挡等情况。此外，视觉导航系统工作时需要对获取的图像进行处理，花费较长时间。故视觉导航系统存在可靠性、实时性等问题。惯性导航技术是唯一同时具有自主、实时、连续、隐蔽、不受干扰，无时间、地点、环境限制的运动信息感知技术，但存在误差随时间累积增大的问题。

本文针对无人机着陆导航问题，结合视觉导航和惯性导航的优缺点，对视觉/惯性组合导航算法[9-11]进行了研究，首先给出了惯性导航在世界坐标系下的误差模型；之后采用姿态、位置双匹配通过Kalman滤波对惯性导航产生的误差进行估计、修正;最后通过仿真验证了算法的有效性。利用视觉导航来辅助修正惯性导航，可以在保证导航精度的同时，满足系统对可靠性、实时性的要求。

1 视觉/惯性组合导航算法概述

无人机在着陆过程中，需要相对于着陆目标的相对位置姿态信息。而惯性导航系统的输出通常是无人机的绝对位置姿态信息，因此本文建立了世界坐标系下惯性导航的模型。在世界坐标系下进行惯性导航可以避免绝对导航信息和相对导航信息之间的互相转换，简化了导航过程中的计算。

视觉导航系统在着陆过程中，可以锁定着陆目标，通过对拍摄的包含着陆目标的图片进行特征提取处理，即可对无人机的相对位姿信息进行解算。本文采用Kalman滤波分别完成位置匹配和姿态匹配，其中位置滤波器将惯导导航解算得到的相对位置与视觉导航估计出的相对位置进行Kalman滤波计算，估计误差速度、水平姿态失调角、加速度零偏；姿态滤波器将惯导惯性系姿态阵和视觉导航系统惯性系姿态阵之间的误差量作为量测量进行滤波，估计视觉导航系统和惯导之间的安装误差、陀螺漂移，并利用估计出的安装误差和视觉导航系统输出的姿态计算惯导系统的航向角。视觉/惯性组合导航算法的主要流程如图1所示。

图1 惯性/视觉组合导航算法原理图Fig.1 Scheme of INS/Vision integrated navigation algorithm

2 视觉/惯性组合导航算法

2.1 坐标系定义

机体坐标系ObXbYbZb：取常用的右前上坐标系。

世界坐标系OwXwYwZw：由于摄像机坐标系并不能给出空间点的具体位置信息，且摄像机在空间中可以安放在任何位置，所以需要一个基准坐标系来描述空间点和摄像机的位置，一般称这个基准坐标系为世界坐标系。本文中世界坐标系与着陆目标固连，三轴分别指向着陆目标的前上右方向。

相机坐标系OcXcYcZc：坐标系原点Oc取无人机质心，OcXc轴指向相机正前方，OcYc指向相机正上方，OcZc指向相机右侧。

地球坐标系OeXeYeZe：原点位于地心，OeXe轴穿越本初子午线与赤道的交点，OeZe轴穿越地球北极点，OeYe轴穿越东经90°子午线与赤道的交点。该坐标系与地球固连。

地理坐标系OnXnYnZn：坐标系原点取无人机所处位置对应地表处，三轴分别指向所在地的北天东方向。

2.2 世界坐标系下的惯性导航误差方程

由于本文采用在世界坐标系下进行惯性导航解算，因此推导了其误差方程，为后文组合导航算法奠定基础：

1)速度误差方程

(1)

2)位置误差方程

(2)

3)姿态误差方程

(3)

2.3 惯性/光学测量组合导航数学模型

2.3.1 位置匹配

1)系统状态方程

(4)

A22=-2A11

2)量测向量和量测矩阵

位置匹配Kalman滤波器的量测量以视觉导航系统为基准的惯导位置误差，由此得到位置匹配量测量和量测矩阵的计算公式为：

Zloc=PI-PC

(5)

(6)

式中，PI表示惯导系统导航解算得到的相对位置参数，PC表示视觉导航系统估计出的相对位置参数。

2.3.2 姿态匹配

本文采用视觉导航系统、惯导相对于惯性系的姿态作为量测信息，可有效减小系统状态方程的复杂度，从而使计算更加快速、准确。

1)惯导惯性系姿态解算

设初始时刻惯导惯性系姿态四元数为[1,0,0,0]，利用陀螺敏感到的相对惯性空间的角增量，即可计算惯导惯性姿态四元数：

(7)

(8)

式中，Δφx、Δφy、Δφz为陀螺输出的角度增量。

2)视觉导航系统惯性系姿态解算

视觉导航系统惯性系姿态矩阵可由下面公式计算得到

(9)

(10)

(11)

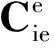
(12)

3)系统状态方程

姿态匹配的系统状态向量为Xatt=[δa,δθ,ε]，其中，δa为3个子惯导惯性系姿态误差角δαx、δαy、δαz，δθ为3个安装角误差δθx、δθy、δθz，ε为3个陀螺漂移εx、εy、εz，则系统状态方程可写为

(13)

4)量测向量与量测矩阵

(14)

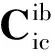
(15)

(16)

(17)

式中，δα⊗为3个惯性失调角构成的反对称矩阵。

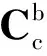
(18)

(19)

将式(19)展开并忽略二次项得

(20)

A+δα⊗A+Bδθ⊗C-Aδθ⊗=I

即

A=I+Aδθ⊗-Bδθ⊗C-δα⊗A

(21)

取矩阵的上三角元素得作为观测量则可得到姿态匹配的量测向量和量测矩阵：

(22)

(23)

3 仿真及分析

假设无人机机体坐标系和世界坐标系重合，速度为0。视觉导航系统和惯导的三轴安装误差分别为dqx=0.6°、dqy=0.3°、dqz=-1°；三轴陀螺常值漂移分别为ex=2(°)/h、ey=3(°)/h、ez=5(°)/h；无人机和着陆目标的相对位置分别为1m、3m、1m；暂不考虑视觉导航系统输出的相对姿态的误差。

在对陀螺漂移等参数进行估计时，需要无人机进行一定的机动将参数分离出来。假定无人机的运动顺序如下：1) 静止10s；2) 以2(°)/s的速度滚转5s；3) 以-2(°)/s的速度转回原位；4) 保持静止；5) 从50s开始以5(°)/s的速度转动航向4s；6) 以-5(°)/s的速度将航向转回原位；7) 保持静止。利用生成的轨迹进行仿真得到安装误差、陀螺漂移及速度误差估计情况如图2～图4所示。

由图2～图4可以看出，视觉导航系统和惯导之间的安装误差、陀螺漂移以及惯导速度误差都得到了很好的估计。在对安装误差的估计中，无人机姿态变化带来量测矩阵的变化，从而使得无人机旋转所绕轴之外的2个安装误差角可观而迅速收敛。从图中还可以看出：无人机滚转后绕Y轴、Z轴的2个安装误差角迅速收敛；而在无人机航向角变化后，绕X轴的安装误差也得到了较为准确的估计。

图2 安装误差估计结果Fig.2 Estimated results of installation error

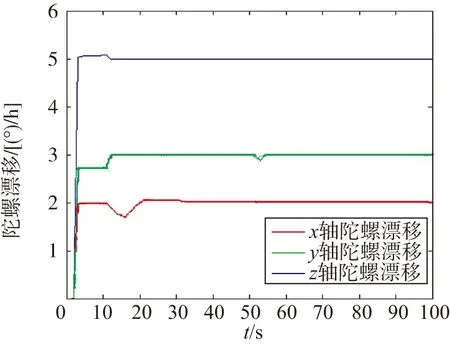
图3 陀螺漂移估计结果Fig.3 Estimated results of gyroscope drift

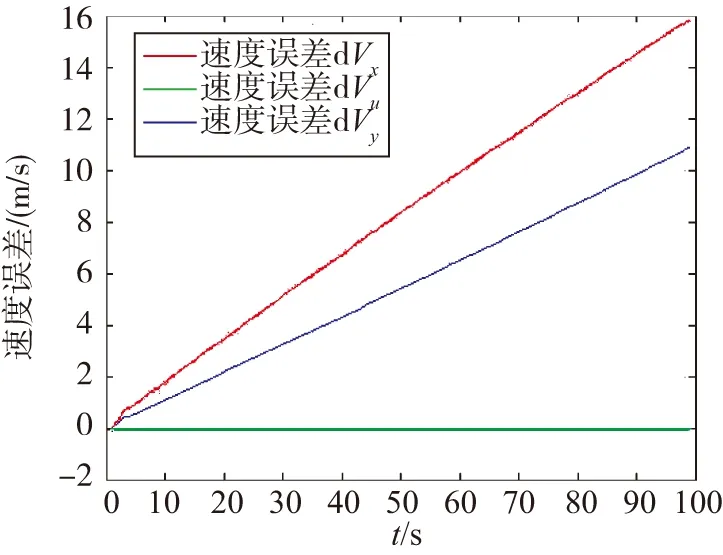
图4 速度误差估计结果Fig.4 Estimated results of velocity error

在上述仿真基础上，加入视觉导航姿态噪声和相对位置噪声，其他条件保持不变。

设加入的3个相对位置噪声为0.1m，仿真得到的速度误差估计结果如图5所示。

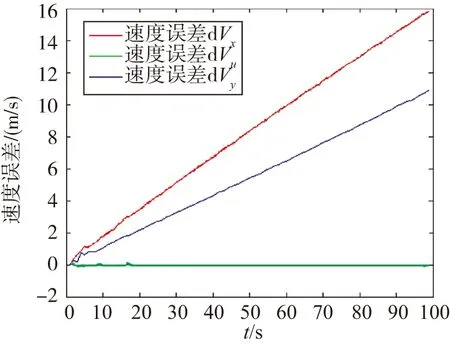
图5 加入噪声后速度误差估计结果Fig.5 Estimated results of velocity error with noise

由图5可以看出，相对位置噪声对速度误差估计结果的影响较小。

设加入的3个姿态角噪声为0.10°。进行12次仿真计算，得到的安装误差角和陀螺漂移估计结果如图6及图7所示。

估计误差如表1所示。

从图6、图7和表1可以看出，加入视觉导航姿态噪声以后，对安装误差以及陀螺漂移的估计带来了一定的影响：绕x轴安装误差估计误差为0.040°(1σ)，绕y轴安装误差估计误差为0.036°(1σ)，绕z轴安装误差估计误差为0031°(1σ)；x陀螺漂移估计误差为0.063°(1σ)，y陀螺漂移估计误差为0.084°(1σ)，z陀螺漂移估计误差为0.077°(1σ)。

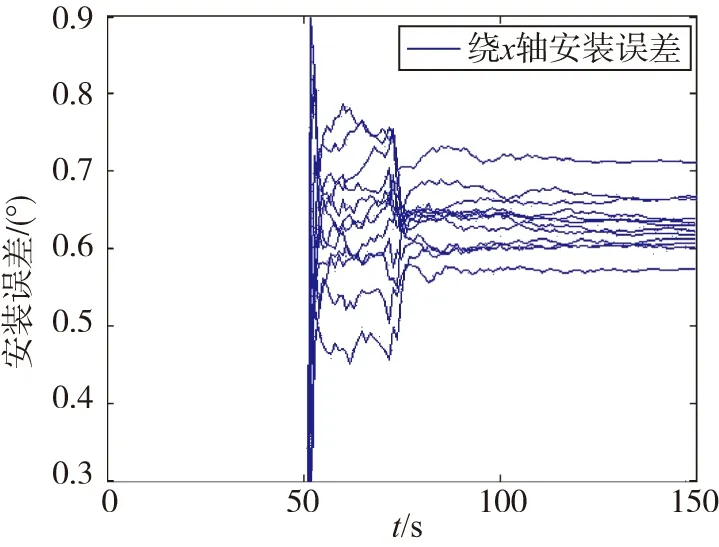
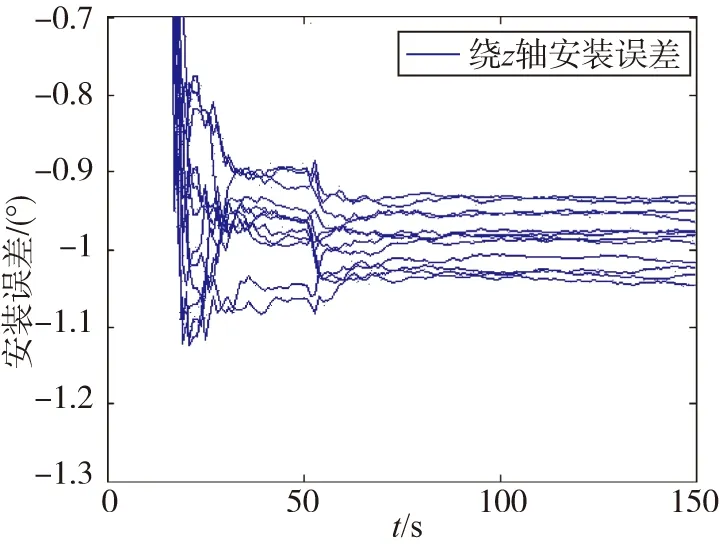
图6 加入噪声后安装误差估计结果Fig.6 Estimated results of installation error with noise

图7 加入噪声后陀螺漂移估计结果

4 结论

本文针对无人机着陆过程对自主性、可靠性以及导航精度的要求，设计了一种视觉/惯性组合导航算法。首先给出了惯性导航在世界坐标系下的误差模型，随后采用Kalman滤波分别完成位置和姿态匹配，利用精度较高的视觉导航系统对惯导进行了修正，抑制了惯性导航误差随着时间的发散。最后通过仿真验证了算法的可行性，对无人机着陆导航具有一定的工程应用价值。

[1] 周树春.基于GPS的无人机自动着陆控制系统设计与实现[D].西安：西北工业大学，2007.

[2] 佚名. 仪表着陆系统[J].航空世界, 2013(4):80.

[3] 张强. 着陆系统发展趋势研究[J].黑龙江科技信息, 2015(27):87-88.

[4] 靳致文.微波着陆系统精度技术研究[J].现代导航,2010,10(5):1-5.

[5] Berdjag D, Pomorski D.DGPS/INS data fusion for land navigation [J].Journal of Donghua University,2004,21(3):88-93．

[6] 管叙军,王新龙. 视觉导航技术发展综述[J].航空兵器,2014(5):3-8.

[7] Fraundorfer F, Scaramuzza D. Visual odometry:Part Ⅱ: Matching,robustness, optimization, and applications[J].IEEE Robotics &Automation Magazine,2012, 19(2):78-90.

[8] Conte G, Doherty P. A visual navigation system for UAS based on geo-referenced imagery[C]// Conference on Unmanned Aerial Vehicle in Geomatics, Zurich,Switzerland, 2011.

[9] Kelly J, Sukhatme G S. Visual-inertial sensor fusion: Localization, mapping and sensor-to-sensor self-calibration [J].The International Journal of Robotics Research,2011, 30(1): 56-79.

[10] Mirzaei F M, Roumeliotis S I. A Kalman filter-based algorithm for IMU-camera calibration: Observability analysis and performance evaluation [J].IEEE Transactions on Robotics, 2008, 24(5): 1143-1156.

[11] 蔡鸣, 孙秀霞, 徐嵩,等. 视觉技术辅助的无人机自主着陆组合导航研究[J].应用光学, 2015, 36(3):343-350.

Navigation Algorithm Based on Inertial/Vision Information Fusion of UAV Autonomous Landing

LIU Chang1, YANG Liang-jun2, LIU Feng1, WANG Yi1, XU Ce1, LIU Chong-liang1

(1. Beijing Institute of Automatic Control Equipment, Beijing 100074, China;2. Military Representative Office of Navy in Kunming Area, Kunming 650000, China)

High-precision navigation information which needs to be real-time and autonomic is essential during UAV autonomous landing. The existing navigation modes have their respective weaknesses and can’t be used indoors. An INSVision integrated navigation algorithm is raised to solve this problem.Mathematical model of inertial navigation in the world coordinate system is built firstly, then position matching and attitude matching by Kalman filtering are presented. Velocity error and accelerometer zero offset are estimated by position matching, installation error angle and gyroscope drift are estimated by attitude matching. The attitude information provided by INS can be corrected by the installation error angle and the attitude information provided by vision navigation system. The simulation results show that this algorithm is feasible.

UAV; Autonomous landing; INS/Vision integrated navigation; Position/Attitude matching

10.19306/j.cnki.2095-8110.2016.06.002

2015-12-11；

2016-03-07。

刘畅(1991 - )，男，硕士，主要从事导航制导与控制方面的研究。E-mail: 839010787@qq.com

V279

A

2095-8110(2016)06-0006-06