地铁候车系统的PH/PH[0，C1]/1/C 批量服务排队模型*

蒋阳升 吴君子 朱娟秀 胡 路

(1.西南交通大学交通运输与物流学院,610031,成都; 2.综合运输四川省重点实验室,610031,成都;3.综合交通运输智能化国家地方联合工程实验室,610031,成都∥第一作者，教授)

地铁候车系统的PH/PH[0，C1]/1/C 批量服务排队模型*

蒋阳升1,2,3吴君子1,2,3朱娟秀1,2,3胡 路1,2,3

(1.西南交通大学交通运输与物流学院,610031,成都; 2.综合运输四川省重点实验室,610031,成都;3.综合交通运输智能化国家地方联合工程实验室,610031,成都∥第一作者，教授)

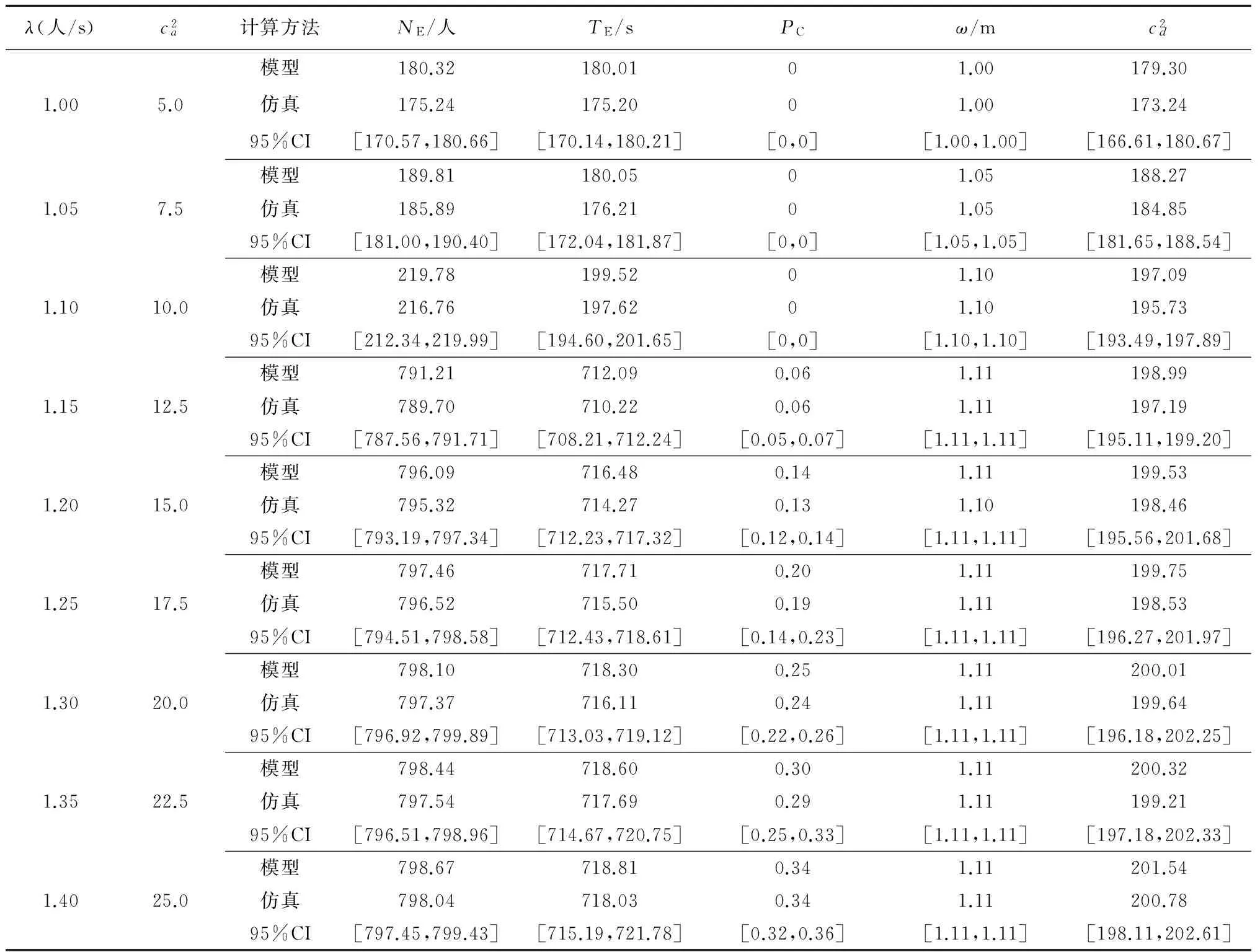
在考虑客流到达和服务随机性的基础上,首先验证了理论上可以逼近任意分布的PH分布能很好地拟合客流到达和服务规律,然后建立了描述地铁候车排队现象的PH/PH[0,C1]/1/C批量服务排队模型,并采用AnyLogic软件仿真验证了模型的通用性和准确性。结果表明，针对9组不同到达率和变异系数的客流数据,仿真模拟和排队模型计算的各项指标的最大绝对误差在0.01～6.06之间,最大相对误差在0.91%～7.69%之间,并且模型结果均在仿真结果的95%置信区间内，故该模型可较好地描述地铁候车排队现象。

地铁候车系统; PH/PH[0,C1]/1/C排队模型; 仿真验证

First-author′s address School of Transportation and Logistics, Southwest Jiaotong University,610031,Chengdu,China

车站是地铁的锚固点,承担乘客的集散和中转功能。候车系统连接着地铁车站和列车,是重要的集散设施,其规划设计直接影响到车站的服务水平和集散效率,进而影响乘客的出行选择。现有地铁设计规范[1-2]采用远期高峰15 min内每列车的上车客流量乘以设计人均面积再除以站台有效长度的方法计算候车系统排队区域的有效宽度,尽管方便应用,但由此配置的候车系统常不能满足运营需求,甚至在未达到远期高峰客流的非高峰时期,也经常出现过度拥挤和乘客候车时间过长的现象,极大地降低了车站服务水平和集散效率,在某些情况下还会成为车站的安全隐患。究其原因,笔者发现,现有设计规范[1-2]本质上相当于采用客流到达间隔和服务时间均服从定长分布D的D/D[0,C1]/1/C排队模型描述候车系统,忽略了客流到达的随机性(即需求的波动性)和服务的随机性(即服务的波动性),导致其无法准确地描述候车系统的排队现象,从而乐观估计了系统的排队性能。文献[3-4]对现有地铁设计规范进行了修正,但本质上仍为采用D/D[0,C1]/1/C排队模型描述候车系统。而事实上,候车系统是一个客流到达间隔随机和服务时间随机的排队系统[5]。因此,上述排队模型对候车系统的描述并不准确,由此设计的候车系统不能满足需求和服务的波动性。

PH分布(phase-type)因理论上可无限逼近任意非负随机变量,且保留了指数分布易于处理的特性,从而具有良好的通用性、解析性和可计算性。其已经取代了指数分布在随机模型解析处理中的地位(指数分布可视为特殊的PH分布),成为排队系统分析、可靠性建模、通信系统效能分析与优化等领域的重要的随机分析工具[6]。因此,大量基于PH分布的排队模型开始涌现,如PH/PH/1[7]、PH/PH/1/C[8]及其网络模型、PH/PH/C[9]和PH/PH/C1/C[10]等,它们可准确地描述大部分排队现象,从而为从排队网络角度准确描述地铁车站交通服务设施系统提供了可能。

本文根据地铁车站候车系统的客流到达和服务特性,建立相应的PH排队模型来准确描述地铁候车系统的排队现象,从而为该系统乃至整个车站交通服务设施系统的合理规划设计奠定基础。

1 建模前准备

1.1 PH分布简介

尽管PH分布理论上可无限逼近任意非负随机变量(例如排队系统的到达时间间隔和服务时间),但却需要确定多达m2+m个参数(m一般不小于2),而在车站的规划设计阶段,给出的客流到达和服务的数据资料有限,无法标定所有参数,从而不便于实际应用。文献[11-12]采用基于数据的到达时间均值(XE)和变异系数c2即可完全确定的简化PH分布拟合一般的非负随机变量取得了很好的效果,为采用PH排队模型进行车站交通服务设施的配置提供了可能。

1.2 系统描述

根据我国《地铁设计规范》[1]和美国TCRP 100[13]“站台设计需保证侯车时候上车乘客尽量不超出乘降区,以避免干扰下车乘客的流通”的规定,以及列车成批搭载乘客的事实,拟将候车系统抽象为有容量限制的A/B[0,C1]/1/C随机批量服务排队系统。其中，A为乘客到达时间间隔分布；B为服务时间分布；C1为列车一次性批量服务的最大人数；C为系统容量,等于乘降区候车区域的容量C2与C1之和。事实上,我国《地铁设计规范》[1]和美国《公共交通通行能力和服务质量手册》[2]计算乘降区宽度时,已将候车系统默认为A/B[0,C1]/1/C排队系统,只不过A和B采用的分布形式为定长分布D,具有简单的解析解。

乘客等候列车时一般在站台的乘降区发生排队现象,且当到站乘客完成下车时,候车乘客排队最长,呈扇形分布在车门两侧的区域 (称为排队区域,即乘降区扣除下车通道),因此研究此时的排队状况更有利于站台的规划设计。

对于图1所示的站台乘降区,乘客以时间间隔分布A到达进行候车;列车以发车时间间隔分布B1到达车站且又以时间分布B2完成了开门和下车;此时,候车乘客开始上车(假设乘客先下后上,符合高峰期的运行情况),直到当前乘客全部上完或达到最大上车乘客数C1时,列车门关闭,驶离站台。

图1 地铁候车系统

如果把相邻两趟列车出现最长排队(为符合站台规划设计的要求,假设不超过排队区域的容量C2)时间点(即下车完成或上车开始的瞬间)的间隔时间作为服务时间,相应的分布记为B(由B1和B2决定,当B2为定长分布时,B即为B1),则所有的候车乘客都需要等待上一服务完成(到站乘客完成下车)才能开始自己的服务(当前乘客开始上车),且列车一次性服务的候车乘客数是批量的,为当前乘客数与最大上车乘客数的较小者(取值区间为[0,C1]，当取值为0时,可认为列车进入一个与B同分布的休假步长V,也可认为列车在为一虚拟的乘客服务)。上述过程既符合实际运行情况,也符合了批量服务排队系统的规则。因此,候车系统的客流与列车可抽象为乘客到达时间间隔分布为A、服务时间分布为B、系统容量C为C1+C2、一次性最大批量服务的乘客数为C1的排队系统,简记为A/B[0,C1]/1/C,C=C1+C2批量服务排队系统。

1.3 候车排队系统到达间隔分布和服务时间分布数据拟合

1.3.1 到达间隔数据拟合

对于候车系统的客流到达间隔分布,文献[14]已验证了简化的PH分布比其它分布(均匀分布、正态分布、定长分布、指数分布、伽马分布、威布尔分布和对数正态分布)可以更好地对其进行拟合。因此本文在此不做赘述。

1.3.2 服务时间数据拟合

候车排队系统服务时间定义为:相继到达的列车的第一个上车乘客的上车时间差。选取深圳市罗球、罗湖和华强等地铁站进行调查,获得有明显服务台设施排队系统的服务时间数据,然后进行数据的随机性检验,最后采用PH分布、均匀分布、正态分布、定长分布、指数分布、伽马分布、威布尔分布和对数正态分布对其进行拟合。拟合效果如图2所示。

图2 候车排队系统的服务时间分布拟合

从图2中可以看出,简化的PH分布、对数正态分布、伽马分布、威布尔分布和正态分布均可以很好地拟合候车系统的服务规律(各分布的累计概率函数的平均可决系数分别为96.74%、96.12%、96.16%、95.03%和94.59%),而定长分布的平均可决系数为72.93%。

1.4 候车排队系统参数标定

1.4.1 到达间隔分布参数标定

在候车系统规划设计时,可参考文献[14]对客流到达间隔PH分布的参数进行标定。

1.4.2 服务时间分布参数标定

(1)

(2)

1.4.3 其它参数标定

候车排队系统的系统容量C为C1+C2,其中C1为列车一次性批量服务的最大人数，是规划设计阶段的给定数据,C2为乘降区候车区域(不包括集散区域和下车流通区域)的容量,与排队区域的面积有关。假设排队区域的长度(沿轨道方向)为L(规划设计阶段一般给定),宽度为W(在车站规划设计时是需要优化的变量),每平方米最大行人数为d(一般取为5人/m2),则C2=[d·L·W]。

2 建立排队模型

2.1 模型建立

研究候车乘客即将上车时的排队状况更有利于站台的规划设计。记此时的候车乘客数为n(n的上限等于C2)。对于该PH/PH[0,C1]/1/C批量服务排队系统的状态,不再只用n表征,而增加到达过程的相位j(1≤j≤mn)、服务过程的相位k(当系统有乘客时,1≤k≤l;无乘客时,则取消这一项)共同定义。因而状态空间U可写为:U={(n,j)| n=0,1≤j≤m1}U{(n,j, k)| 1≤n≤C1,1≤j≤mC1,1≤k≤l}U{(n,j, k)| C1

(3)

其中,Tn0=-Tn·e,n=1,2,…,C1;En,n=diag(1,1,…,1)mn×mn,n=1,C1;En,n-1=diag(1,1,…,1)mn×mn-1,n=2,3,…,C1;El=diag(1,1,…,1)l×l; S0=-S·e;T⊗S和T⊕S分别为矩阵T和S的Kronecker乘积与Kronecker和。

该准生灭过程的稳态概率向量π能通过求解下面的全局平衡等式获得：

(14)

其中，向量p0=(0,0,…,0),其元素个数等于向量π的长度;向量π=(π0,π1,…,πC2),π0=(π01,π02,…,π0m1)为水平q0的稳态概率向量, πn=(πn,1,πn,2,…,πn,mn·l),1≤n≤C1和πn=(πn,1,πn,2,…,πn,mC1·l),C1

为避免巨大的存储需求,在SOR(超松驰算法)迭代求解技术的基础上进行改进,以适应Q的特殊结构。即只存储非零的对角块的矩阵,从而显著降低算法的复杂度。采用MATLAB软件编写程序获得稳态概率向量π,同时采用下列公式计算所需数量指标,即候车排队系统的平均候车乘客数NE、堵塞概率PC和平均候车时间TE。

(15)

(16)

(17)

其中,λ-πC·(T0⊗El)·e为乘客的输出率或有效到达率。

(18)

(19)

2.2 模型准确性的仿真模拟验证

表1 仿真模拟和排队模型计算的指标比较

3 结语

本文采用PH分布拟合候车系统的客流到达和服务规律,从而建立具有解析性和通用性的PH/PH[0,C1]/1/C批量服务排队模型,并通过AnyLogic仿真验证了模型的有效性和准确性。该模型比现有主要模型D/D[0,C1]/1/C更加准确地描述了地铁站台排队现象。理论上本模型不仅可用于描述地铁候车系统的排队现象,还可用于描述公交站台和垂直电梯系统的排队现象。另外,由于PH排队模型的离去间隔分布也为PH分布[16],因此,本文PH/PH[0,C1]/1/C批量服务排队模型还可用于搭建车站交通服务设施系统的PH排队网络模型。需要说明的是,本文将候车系统的服务台定义为1个,且假设了乘客先到先服务,与实际情况(即服务台数量为多个,且乘客可互相超越彼此)存在一定差距。后续研究可对本模型进一步改进。

[1] 中华人民共和国住房与城乡建设部.地铁设计规范：GB 50157—2003[S].北京：中国建筑工业出版社，2004.

[2] NFPA.NFPA130 Standard for fixed guideway transit and passenger rail systems 2007[S].Quincy:National Fire Protection Association,2006.

[3] 王丽华.地铁车站站台设计[J].北方交通,2008(4):220.

[4] 王甲子.地铁车站站台宽度计算方法改进及仿真评价[J].交通运输系统工程与信息,2012,10(12):168.

[5] JIANG Y S,HU L,ZHU J X,et al.PH fitting of the arrival interval distribution of the passenger flow on urban rail transit stations[J].Applied Mathematics and Computation,2013,225:158.

[6] 田乃硕,李泉林.PH分布及其在随机模型中的应用[J].应用数学与计算数学学报,1995,9(1):1.

[7] LATOUCHE G,RAMASWAMI V.The PH/PH/1 queue at epochs of queue size change[J].Queueing Systems,1997,25(14):97.

[8] ALFA A S,ZHAO Y Q.Overload analysis of the PH/PH/1/K queue and the queue of the M/G/1/K type with very large K[J].Asia Pacific Journal of Operational Research,2000,17(2):123.

[9] MIYAZAWA M,SAKUMA Y,YAMAGUCHI S.Asymptotic behaviors of the loss probability for a finite buffer queue with QBD structure[J].Stochastic Models,2007,23(1):79.

[10] KRISHNAMURTHY A,SURI R,VERNON M.Analysis of a fork/join synchronization station with inputs from Coxian servers in a closed queuing network[J].Annals of Operations Research,2004,125(1):69.

[11] SADRE R,HAVERKORT B,OST A.An efficient and accurate decomposition method for open finite-and infinite-buffer queueing networks[C]∥3rd Int.Workshop on Numerical Solution of Markov Chains.UK,1999.

[12] WEERSTRA A J.Using matrix-geometric methods to enhance the QNA method for solving large queueing networks[D].Netherlands:Master′s thesis, University of Twente,1994.

[13] Transportation Research Board.Transit capacity and quality of service manual[M].2nd ed.Beijing:China Building Industry Press,2010.

[14] 孙继东.城市轨道交通车站乘客服务设施客流到达分布规律研究[D].成都:西南交通大学,2014.

[15] 胡路.考虑稳定性的城市轨道交通车站交通服务设施系统优化配置理论与方法[D].成都:西南交通大学,2014.

[16] HU L,JIANG Y S,ZHU J X,et al.Hybrid of the scatter search, improved adaptive genetic, and expectation maximization algorithms for phase-type distribution fitting[J].Applied Mathematics and Computation,2013,219(10):5495.

PH/PH[0,C1]/1/CBatch Service Queuing Model in Metro Waiting System

JIANG Yangsheng, WU Junzi, ZHU Juanxiu, HU Lu

With a full consideration of the potential passenger arrival and the randomness of service, the PH (hydrogenion concentration) distributions that can fit well with the law of potential passengers and services are demonstrated in theory. Then, the related model that describes metro waiting queues of PH/PH[0,C1]/1/Cis established. In which, AnyLogic software simulation is used to analyze and verify the versatility and accuracy of the model. The results indicate that the maximum absolute error of the calculated simulation and queuing model indicators is between 0.01～6.06, based on 9 different set arrival rates and variation coefficient of the passenger flow data, and the relative maximum error is between 0.91%～7.69%. Thus, the model results are in 95% confidence interval in the simulation results, thus verify the reliability of this model.

metro waiting system; PH/PH[0,C1]/1/Cqueuing model; simulation and verification

*国家自然科学青年基金项目(51108391); 西南交通大学优秀博士学位论文培育项目

F 224.34∶U 231.4

10.16037/j.1007-869x.2016.07.003

2014-05-04)