城市轨道交通应急钢梁在列车作用下的动力响应

田国栋

(中铁第一勘察设计院集团有限公司，710043，西安∥工程师)

城市轨道交通应急钢梁在列车作用下的动力响应

田国栋

(中铁第一勘察设计院集团有限公司，710043，西安∥工程师)

建立了87型应急钢梁与轨道交通列车的车桥耦合分析模型,它由车辆模型和有限元桥梁模型两部分组成。对具有2个转向架的4轴拖车和4轴动车分别建立了27、17个自由度的车辆动力分析模型。以轨道不平顺作为车桥耦合系统的自激激励源,运用模态综合技术,建立了车-桥系统耦合振动的运动方程组,通过编程进行计算分析。以三种不同跨度87型下承式钢桁梁为例,模拟运行中列车驶入、驶出桥梁的整个过程,计算分析了钢桁梁的自振频率、振型特点，以及钢桁梁在列车通过时的动力响应规律,得出重要结论,从而为进一步研究87型应急钢桁梁的动力特性提供可行的研究方法。

城市轨道交通; 应急钢桁梁; 车桥系统; 动力响应

Author′s address China Railway First Survey & Design Institute Group Co.,Ltd.,710043,Xi′an,China

1 工程背景

随着城市轨道交通的发展,高架结构凭其经济节约、施工进度快等优点,在城市轨道交通工程中占据越来越大的比重。考虑高架桥梁由于自然灾害、工程质量事故等原因造成的应急抢修问题及其战备功能,城市轨道交通应急抢修梁的研究显得尤为重要。

应急钢桁梁是一种全焊构架、明桥面体系的拆装式钢桁梁。该类结构的主要特点是杆件种类较少、结构较轻便、施工简易、架设速度快。其主要用于战时及紧急情况下桥梁上部结构的应急抢修,并在施工便桥、简易架桥机、龙门吊等施工设备中广泛应用。我国从建国初期即开始了应急抢修梁的研究工作,相继研制了适用于中等跨度桥梁的64式应急军用梁和加强型64式应急军用梁,以及最大跨度能够达到96 m的87式应急钢梁。

国内对于应急钢梁的研究多偏向于静载条件下的内力分析计算[1-2]及应急梁在结构施工中的应用[3-4]，但对应急钢梁的动力性能,尤其是列车通过时应急梁动力特性的研究非常少。考虑到应急钢桁梁重要的战略意义,结合该类结构特殊的设计特点,对应急钢桁梁在运行列车作用下的动力响应规律进行研究,以便对桥梁结构自身振动特性和桥上列车运行时的安全可靠性作出评价,确保在各种状态下结构的可靠性。

2 列车作用下桥梁振动分析模型

87型应急钢桁梁在运行列车作用下的空间振动分析模型,由车辆模型和桥梁模型两部分组合而成[6-7]。前者是由拖车和动车组成的列车。每节拖车或动车又是由车体、转向架、轮对及弹簧-阻尼悬挂装置等组成的多自由度振动系统。建模时,将车体、转向架和轮对均视为刚体，每节车体、转向架各考虑5个自由度,每组轮对考虑3个自由度。本文采用A型车四轴拖车,自由度数共计27个;采用A型车四轴动车,但不考虑转向架的独立自由度数,自由度数共计17个。车辆动力分析模型如图1所示。

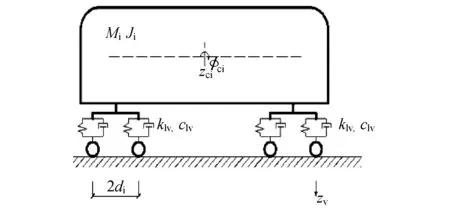
图1 车辆动力分析模型

应急钢桁梁则由钢桁梁、桥面系、轨道、支座等组成。车辆轮对上的力通过钢轨传递到桥梁结构上。研究桥梁和车辆系统的横、竖向振动时,一般采用空间分析模型进行分析,并假定钢轨与桥面之间没有相对位移,同时忽略轨枕及扣件的弹性变形。

除了运行车辆的重力加载,车桥系统振动的最重要的激励源为轨道不平顺[8-9]。通过随机过程理论来模拟轨道不平顺,利用已知轨道不平顺谱密度模拟出三个方向上的轨道不平顺样本:方向(横向)不平顺Ys(x)、高低(竖向)不平顺Zs(x)和水平(扭转)不平顺θs(x)。第i节车第j个转向架第l个轮对的位移Ywijl、θwijl、Zwijl可表达为所在位置处的桥梁位移Yb、θb、Zb与轨道不平顺的叠加:

(1)

式中:

xijl——第i节车第j个转向架第l个轮对沿桥梁长度的位置;

h4i——车轮中心线至梁截面中心线的高度。

采用式(1)中车辆和桥梁的位移衔接条件,消去车辆振动方程及桥梁有限元模型中的不独立自由度,可得到由87型应急钢桁梁与列车组成的动力系统的耦合运动方程:

(2)

式中:

下标v,b——分别表示车辆和桥梁;

M，K，C——分别表示体系的质量、刚度、阻尼矩阵;

Fvb，Fbv——车辆与桥梁之间的相互作用力。

当列车在桥上通过时,各轮对的位置不断改变,式(2)中的系数也随之不断变化,使得车桥耦合系统动力方程组成为一个时变系数的二阶线性微分方程组。方程求解采用数值积分法。

3 下承式钢桁梁的动力特性分析

根据列车作用下应急钢桁梁振动分析理论,本文采用北京交通大学土建学院自编程序进行计算分析,以64m、72m及80m三种不同跨度的87型下承式钢桁梁为例,分析应急钢桁梁在运行列车作用下的振动响应。

3.1 自振特性分析

87型下承式钢桁梁梁体材料采用15Mn低合金钢，桁梁高度为8.68m,宽度为5.388m,节间距为4m。其有限元空间分析模型如图2所示。

钢梁前10阶自振频率计算结果见表1。由表1可见,由于三种跨度钢桁梁的主桁高、梁宽、节间距等几何尺寸完全相同,只是跨度不同,因此三种跨度下承式梁的前10阶振型特点是基本相同的;随跨度增大,结构刚度逐渐降低,故相应的自振频率逐步减小;跨度对竖向自振频率的影响比横向和扭转都要大。

观察结构的自振频率分析结果可知,结构一阶横、竖向自振频率均较低,接近《铁路桥梁检定规范》和《铁路桥涵设计基本规范》中规定的最小限值,说明梁的横、竖向刚度均较弱。另外,在结构前10阶振型中,扭转振动出现了3次,表明梁的抗扭刚度也较差。因此,对列车作用下桥梁的振动性能进行分析评价尤为重要。

3.2 列车通过时桥梁的动力响应分析

本文模拟了城市轨道交通A型车8辆编组(6动2拖)列车通过87型下承式军用钢桁梁时的动力响应。计算车速取为30～70km/h。根据设计车速及目前城市轨道交通养护水平,采用美国5级功率谱模拟产生的轨道高低、方向及水平不平顺样本作为系统的激励源。

图3～4是三种不同跨度的87型下承式钢桁梁在列车以45km/h的速度通过时,跨中横、竖向动位移响应的时程曲线。从图3～4中可以看出,随着跨度增大,桥梁的横、竖向位移均有明显增大,且竖向位移受桥梁跨度的影响更为明显。当下承式梁跨度达到80 m时,横向最大振幅Amax为0.529 cm,而竖向振幅已经超过7 cm。

图2 三种跨度下承式钢桁梁有限元分析模型示意图

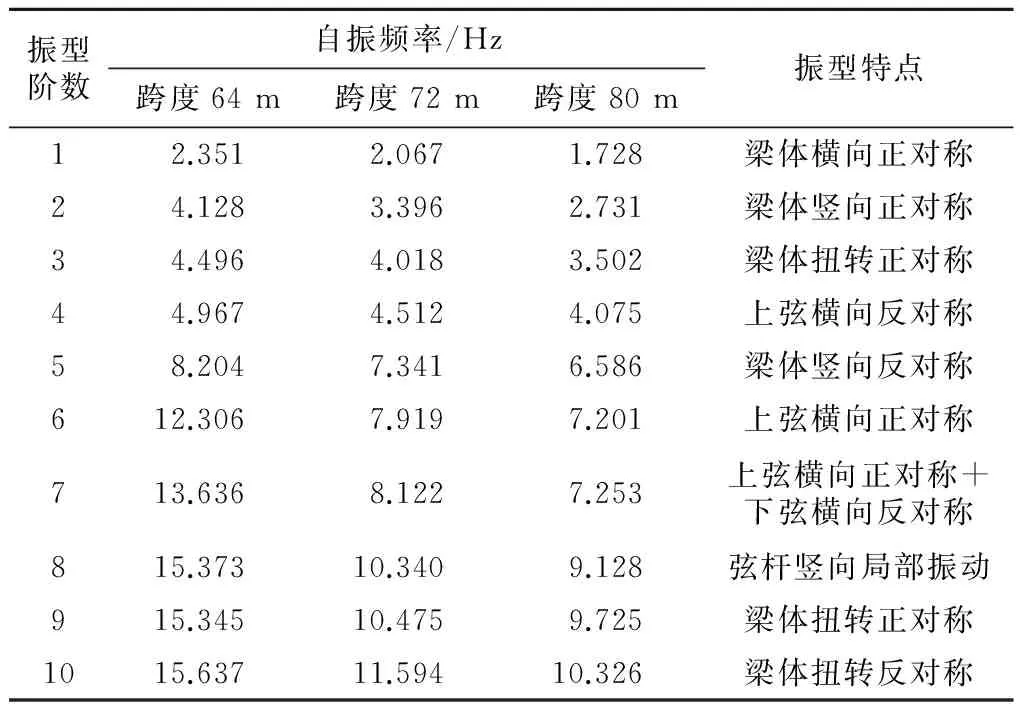
振型阶数自振频率/Hz跨度64m跨度72m跨度80m振型特点12.3512.0671.728梁体横向正对称24.1283.3962.731梁体竖向正对称34.4964.0183.502梁体扭转正对称44.9674.5124.075上弦横向反对称58.2047.3416.586梁体竖向反对称612.3067.9197.201上弦横向正对称713.6368.1227.253上弦横向正对称+下弦横向反对称815.37310.3409.128弦杆竖向局部振动915.34510.4759.725梁体扭转正对称1015.63711.59410.326梁体扭转反对称

图5～6给出了三种跨度的87型下承式钢桁梁在列车以45 km/h的速度通过时,桥梁跨中截面加速度响应的时程曲线。从图5～6可以看出,随着跨度增大,桥梁刚度降低,桥梁横向和竖向加速度响应均逐渐增大。但与位移响应相比,加速度响应受桥梁跨度的影响要小。

图7给出了不同跨度桥梁跨中竖向动力响应幅值随列车速度的变化曲线。计算结果表明,速度在30～70 km/h范围内,桥梁的跨中挠度受车速影响不明显,而竖向加速度随车速不断增大表现出逐渐增大的趋势;在车速相同的情况下,随着桥梁跨度的增加,桥梁的跨中挠度明显增大,竖向加速度也有增加,但加速度峰值受跨度的影响不太明显；80 m跨度的应急钢桁梁的跨中竖向挠度已超过7.0 cm,超出了规范限值。

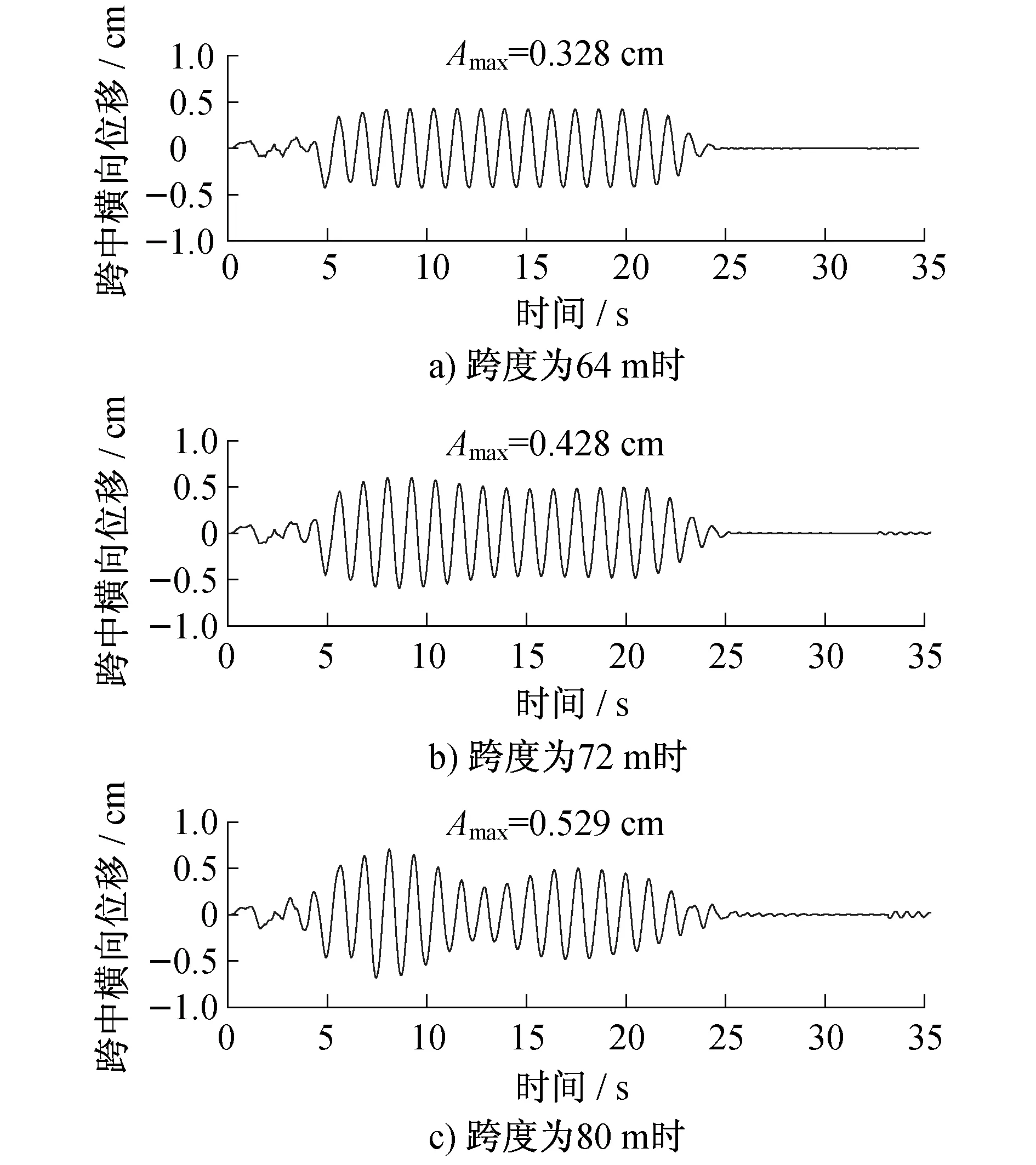
图3 不同跨度桥梁跨中横向位移响应时程曲线(v=45 km/h)

图4 不同跨度桥梁跨中竖向位移响应时程曲线(v=45 km/h)

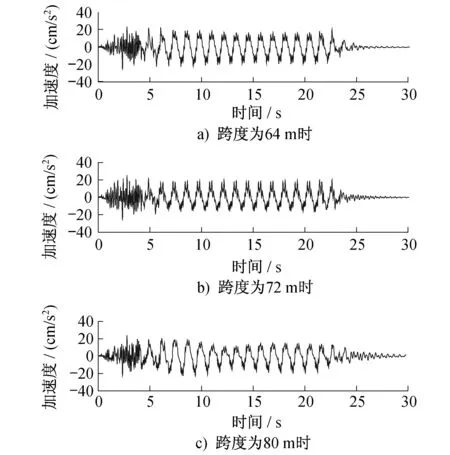
图5 不同跨度桥梁跨中横向加速度响应时程曲线

图6 不同跨度桥梁跨中竖向加速度响应时程曲线

图8给出了不同跨度桥梁跨中下弦横向动力响应幅值随列车速度的变化曲线。结果表明,在车速30～70 km/h范围内,跨中横向位移受车速的影响比较大,在车速为48 km/h附近达到峰值，横向加速度响应则随车速不断增大表现出逐渐增大的趋势;在运行车速相同的条件下,随跨度增加,位移基本呈增大趋势,而加速度受跨度影响不太明显;当车速为48 km/h时,80 m跨度梁横向位移已达到7.2 mm,接近《铁路桥梁检定规范》中规定的行车安全限值,该情况应引起足够的重视。

图7 不同跨度桥梁跨中竖向动力响应随列车速度的变化

4 结语

本文建立了城市轨道交通高架桥采用的87型应急钢桁梁与列车的动力相互作用空间分析模型。以美国5级谱生成的轨道不平顺样本作为车-桥系统激励源,分析了64 m、72 m、80 m三种不同跨度的87型下承式简支钢桁梁的车桥系统动力响应,得到如下结论:

(1) 应急钢桁梁的整体刚度比较差,结构的横、竖向自振频率均较低。对于三种不同跨度桥梁,随着桥梁跨度的增大,结构的刚度逐渐减小,结构自振频率逐渐降低。

(2) 应急钢桁梁的动力响应随列车速度的增加而增大,其中,车速对加速度响应的影响更为显著。当车速达到48 km/h时,桥梁的横向位移达到峰值,80 m跨度梁的横向位移已接近限值。此时应考虑限速行驶。

图8 不同跨度桥梁跨中横向动力响应随列车速度的变化

(3) 相同列车运行速度下,应急钢桁梁动力响应随跨度增大而增大。尤其当跨度达到80 m时,跨中横向、竖向位移响应值均已超过规范规定的限值,故在实际工程中,跨度在80 m以下的应急梁宜优先采用。

[1] 贾国林.六四式铁路军用梁改进研究[J].国防交通工程与技术，2009,7(2):13.

[2] 张庆海,张亚齐,刘嘉武，等.铁路抢修钢梁仿真分析探讨[J].国防交通工程与技术,2005,3(4):24.

[3] 唐重平,李海云.六四式军用梁在大跨度简支梁架设中的应用[J].桥梁建设，2002(4):74.

[4] 王新敏,王海林.六四式军用梁在桥梁施工中的应用技术[J].铁道建筑技术，2001(4):14.

[5] 张艳萍,伊洪建,李海超，等.单层六四式铁路军用梁在现行铁路活载条件下的使用研究[J].铁道建筑，2007(4):9.

[6] 李小珍,强士中.列车-桥梁耦合振动研究的现状与发展趋势[J].铁道学报，2002,24(5):112.

[7] XIA H.Dynamic analysis of train-bridge system and its application in steel girder reinforcement [J].Computers and Structures，2001,79:1851.

[8] 高芒芒.高速铁路列车-线路-桥梁耦合振动及行车走行性研究[J].中国铁道科学，2002,23(2)：135

[9] 夏禾,张楠.车辆与结构动力相互作用[M].北京:科学出版社,2005.

Dynamic Response of Rail Transit Emergency Steel Beamunder the Train Action

TIAN Guodong

A spatial analysis model of 87-type emergency steel beam in the train-bridge-coupling system is builtin this paper, which is made up of the train model and the finite element bridge model.Then the dynamic analysis models with 27 degrees of freedom and 17 degrees of freedom are respectively built for the four-axis locomotive and the four-axis van, both have two bogies. By taking the track irregularity as the self-excited excitation source in the train-bridge-coupling system, the motion equations of the coupling about train and bridge are established,which are calculated through program composition. The steel truss beam of 87-type with three different spansare taken as the example,the whole process of the train running into and out of the bridge is simulated, the self-vibration and the dynamic response characteristicsare analyzed. On this basis,some important conclusions are obtainedthat could provide a possible approach for further research on the dynamic performance of 87-type emergency steel truss beam.

urban rail transit; emergency steel truss; train-bridge system; dynamic response

U 441+5: U 448.36

10.16037/j.1007-869x.2016.07.011

2016-03-22)