数据约简化的高光谱影像端元提取

徐 君，宋 凯，李 波，蔡体健，王彩玲



数据约简化的高光谱影像端元提取

徐 君1，宋 凯1，李 波1，蔡体健1，王彩玲2

（1. 华东交通大学信息工程学院，江西 南昌 330013；2. 西安石油大学计算机学院，陕西 西安 710065）

提出一种利用图像的空间结构信息在特征空间中设计大小适宜的超球，将单形体的顶点分隔在超球外部，剔除超球内部的数据，只保留超球外部的少量数据参与端元提取算法。经过分析，该方法可以大大减少端元提取算法的运算量。通过实验对比，用相关端元提取算法对简化后的数据进行端元提取的结果精度很高，与简化前数据的端元提取结果吻合。

高光谱遥感；端元提取；空间结构信息；超球；混合像元分解

0 引言

混合像元在高光谱图像中的广泛存在已成为高光谱遥感技术向定量化方向发展的主要障碍之一。混合像元分解能够打破高光谱图像空间分辨率较低的限制，可以使像元分类进入亚像元级别，从而大大改善高光谱图像分类的精度[1]。端元就相当于一个像元里的亚像元，它只包含一种地物的光谱信息。混合像元分解就是要确定像元中包含哪些端元及几种端元在这个像元中的面积百分比。目前较为成熟且常用的端元提取算法有基于单形体几何学的PPI（Pixel Purity Index）算法[2-3]、SGA（Simple Genetic Algorithm）[4]算法和VCA（Vertex Content Analysis）算法[5-6]等，这些算法由于需要图像中所有像元都参与运算，因此导致计算量很大，端元提取的速度较慢。本文提出一种数据约简化的端元提取方法，在特征空间中设计超球，剔除那些超球内部那些不可能成为端元的像元，只保留超球外围那些有可能成为单形体顶点的像元参与端元的提取算法，由此大大减少了运算量，提高了端元提取算法的运算效率。

1 超球约简高光谱数据的思想

Boardman[7]创造性地提出了利用凸面几何学分析的方法提取图像端元的雏形，他认为高光谱数据点在特征空间中均包含在一个凸面单形体内部，单形体的顶点分别对应图像中的纯像元即端元，并据此发展了纯像元指数（PPI）提取端元的算法。在以后发展的众多的基于凸面几何学原理的端元提取算法如N-FINDR、VCA算法中，都是通过寻找凸面单形体的顶点来进行端元提取的。位于单形体内部的数据不可能是端元光谱，只有外围的少数光谱才有可能是要提取的端元光谱。如果能将单形体内部那些不可能成为顶点的光谱数据剔除，只保留有可能成为单形体顶点的数据参与端元提取算法，则会大大提高端元提取的效率。具体做法以整幅高光谱图像的均值光谱作为球心，合理选取半径设计超球，剔除超球内部的数据点，仅保留超球外围的有可能成为凸面单形体顶点的数据参与端元提取。用表示每个像元的光谱向量，以二维空间为例，如图1所示，像元光谱在特征空间中呈一个凸面单形体的结构。

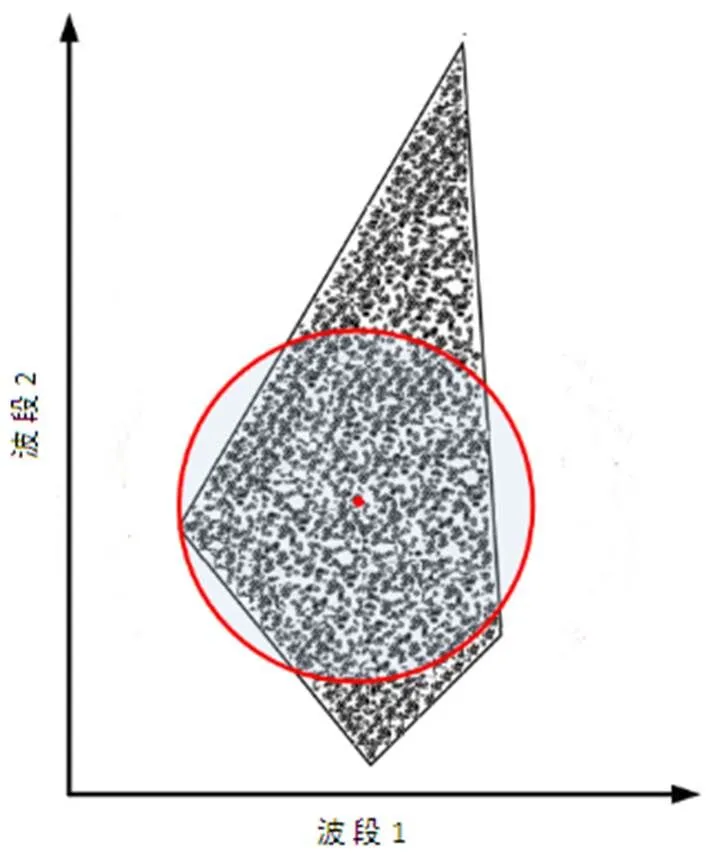
图1 二维空间中设计超球约简高光谱数据

以距离球心最近那个单形体顶点到球心的距离作为半径设计超球。这样既可以保证所有单形体顶点都被划分到超球壳之外，又能最大限度地简化参与端元提取算法的高光谱数据。具体思路如下：

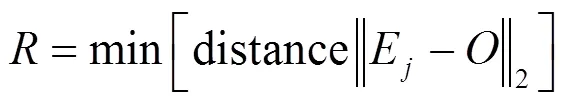
4）剔除超球内部的点，只保留超球外部的像元参与端元提取算法。

在上述的思路中，如何设计超球的半径成为问题的关键所在。如果半径选择过大，则可能将某些潜在的端元剔除掉，造成端元提取的误差；而如果超球半径选择过小，那么大量的数据被保留下来参与端元提取，起不到简化数据并提高运算效率的目的。本文采用结合图像的空间信息来寻找距离球心最小的端元以设计超球的半径。

2 结合图像空间结构信息设计超球

自然界中的地物分布大都具有一定的空间结构（比如道路、房屋、耕地、森林等），地物在空间上一般是成片出现的，具有连续性，如果某点处为A类地物，那么其周围像素点也是A类地物的可能性极大。2004年耿修瑞提出一种基于空间连续性的高光谱图像分类方法[8]，该方法可以在兼顾像素点空间相邻的同时，又要求光谱特征相似，因此可以认为被划入同一块的像素点属于同一类，或者至少是混杂有该类地物的混合像素点，对大多数高光谱图像，这样的假设是合理的。采用该方法用合适的阈值对图像进行分块后，不需要再进行分类，计算每一子块的均值光谱与整幅图像的均值光谱（球心）之间的距离，遍历所有子块图像后，找出所有距离中的最小者。在这个最小者所在子块内，再求取与图像的均值光谱距离最大的像元，将这个像元到球心的距离作为设计超球的半径。

上述做法实际上是将距离球心最近的一个单形体顶点到球心的距离作为超球半径，这样既可以约简高光谱数据又可以保证所有单形体顶点被分割到超球壳的外围。这样做的理论依据是：由于在图像空间分块中考虑了空间相关性和光谱相似性的结合，只要选择合适的阈值控制图像被分块为一定的规模，那么被分入同一图像块内的像元在光谱特征空间的散点图中必然距离较近而聚集在一起，而其中的纯像元（或者最纯的像元）作为其中的凸点，相比较子块内的其他像元，必然是距离整幅图像总的均值光谱最远的一个。具体操作步骤如下：

1）采用文献1中的方法对图像进行空间分为S块（为图像被分割的子块数目）；

3）在子块图像*的所有像元中，计算并找出与球心的距离最大者，并将这个距离作为半径设计超球；

4）将超球内部的数据，也就是将特征空间中与球心距离小于的像元剔除，只保留超球壳上及壳外的数据参与端元提取；

5）对超球约简后的数据进行端元提取。

上述算法中，采用文献[7]中的方法对高光谱图像分块时，对图像中的每个像元仅需要计算和比较与其相邻的少数几个像元的欧氏距离，分块后也仅需计算和比较子块图像内像元及均值光谱与和球心的距离，就可以得出超球的半径对高光谱数据进行约简。采用基于凸面单形体的端元提取方法对上述方法约简后的高光谱数据进行端元提取。因为剔除大量冗余的混合像元，无疑会大大减小所需的运算量和复杂度。

3 算法验证与分析

实验中采用美国内华达州Cuprite地区AVIRIS数据的一部分进行算法的验证，其假彩色合成图如图2所示。该地区位于沙漠，表观地物主要为裸露的矿物，并且各种矿物之间的混合现象较为普遍，Swayze和Clark等人已经给出了该地区的地物真实分布的报告[9]。该图像有200×200个像元，移除信噪比太低或水汽吸收严重的波段, 剩下188个波段的光谱图像用于端元提取[10]。

图2 Cuprite区域的AVIRIS数据假彩色合成图

首先利用文献[7]中的方法，以光谱角距离做为光谱相似性的度量，取光谱角距离阈值为12，最终得到的分块图像如图3，再求每块的均值光谱，计算每一子块的均值光谱与整幅图像均值光谱（球心）的欧式距离，标出其中距离最小者所在的子块图像，在这个图像子块中找出与球心距离最大的像元，将这个像元与球心的距离作为半径设计超球。最终有30120个像元因被划入超球内部而被约简掉，参与端元提取的像元只有9880个，通过设计超球约简后参与投影计算的像元数目减少了3/4以上。

图3 约简后剩余的像元分布图

采用N-FINDR算法对数据约简前整幅图像200×200个像元及数据约简后的9880个像元进行端元提取，端元数目设定为9。经过比较后，发现同一种算法对约简前后的数据的端元提取结果高度相似。图4中(a)图和(b)图分别为采用N-FINDR算法对约简前后数据的端元提取结果。

为了进一步衡量上述方法的端元提取效果，初始化端元数目为9，分别用N-FINDR、VCA和SGA算法对上述超球约简后的高光谱数据进行端元提取，得出各算法在数据约简后的端元提取时间列于表1，可以看出数据约简后端元提取的运算效率大大提高。通过以上3种算法得到端元后，再分别通过全约束最小二乘法解混，将光谱分解得到的丰度图与实地勘测报告比较后可以确定各端元对应的矿物，然后与美国地质调查局（USGS）库中相应矿物的光谱进行对比[11]，计算它们的光谱夹角距离如表2所示，图5为在美国地质调查局（USGS）库中提取的对应于表2中所有矿物的光谱。

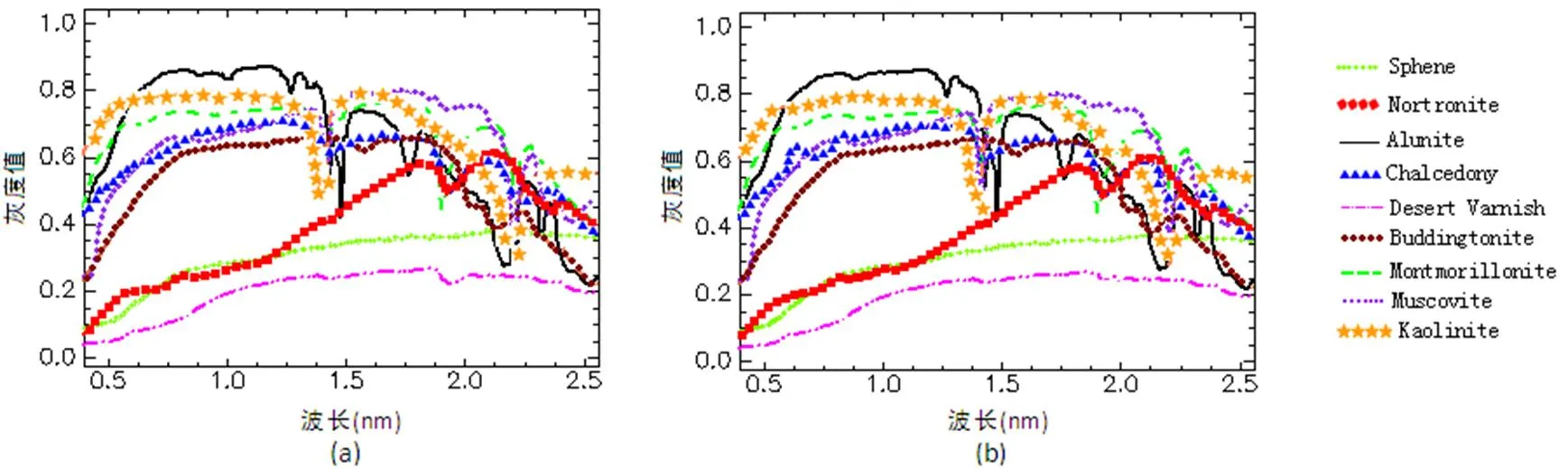
图4 N-FINDR算法对约简前后数据的端元提取结果

表1 数据约简前后端元提取耗时比较

从表2可以看出，对约简后和约简前的高光谱数据分别采用N-FINDR、VCA和SGA算法进行端元提取的结果相比，总体上提取精度相当。

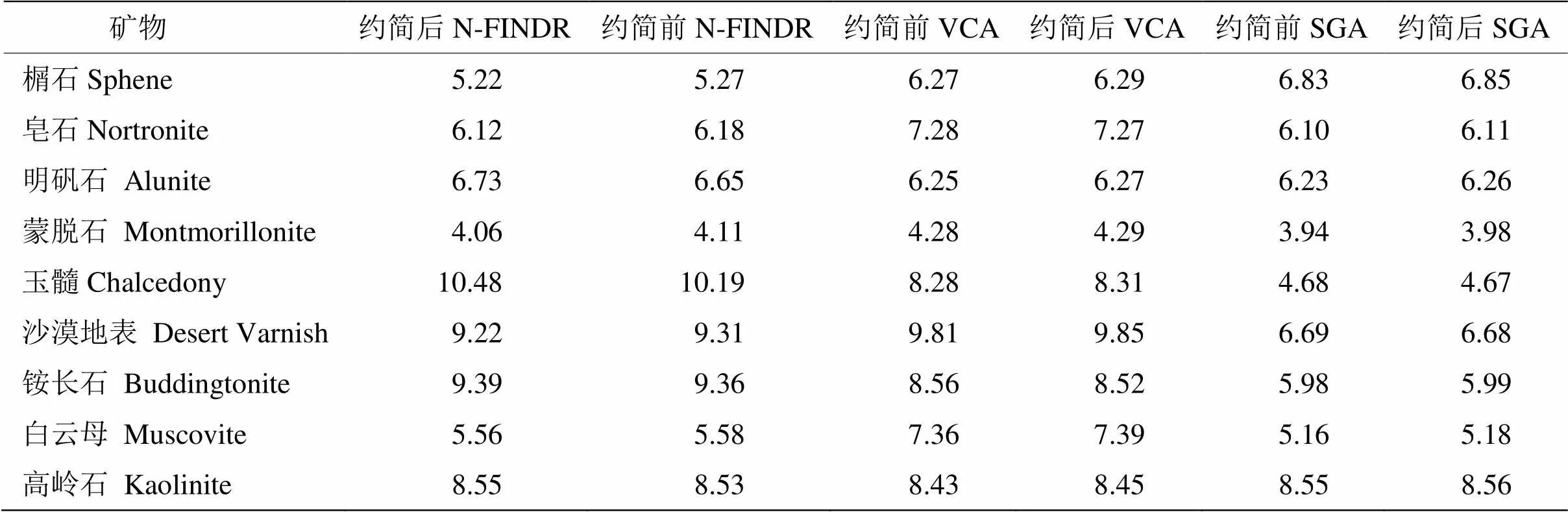
表2 数据约简前后所提取的端元与USGS光谱库中光谱之间的光谱夹角距离

图5 美国地质调查局（USGS）库中对应表2矿物的光谱

4 结论

目前现有的基于凸面几何学原理的端元提取算法都是通过寻找单形体的顶点作为端元光谱来进行提取，其需要高光谱图像上所有像元都参与运算，因此均有运算量大，端元提取效率较低的缺点。鉴于此，本文首先从简化参与运算的高光谱数据的角度，提出首先利用图像的空间信息分块，根据分块的结果在特征空间中建立超球模型，将最有可能成为单形体顶点的小部分像元分割在超球壳外围，位于超球内部的数据不再参与端元提取算法。经过分析，设计超球模型增加的运算量很小，而高光谱数据简化后的几种基于凸面几何学的端元提取算法中减少的运算量很多，两者差距较大，因此本文方法能够大大提高端元提取的效率。最终实验数据也表明，采用本文方法约简高光谱数据后进行端元提取，与采用相同算法对约简前的数据提取的端元相比，提取的精度相当，但运算效率明显提高。本文方法要求在端元提取之前需要对图像进行分块并设计超球面，这需要增加额外的运算量。对图像分块和超球面设计的运算量进行定量分析，并与端元提取中减少的运算量进行比较，是下一步要进行的研究工作。

[1] 徐君, 展爱云, 刘志伟. 基于OSP与NMF的光谱混合像元分解方法[J]. 华东交通大学学报, 2013, 30(1): 5-9.

XU Jun, ZHAN Aiyun, LIU Zhiwei, et al. Spectral unmixing based on OSP and NMF[J].Journal of East China Jiaotong University, 2013, 30(1): 5-9.

[2] Bateson A, Curtiss B. A method for manual endmember selection and spectral unmixing[J]., 1996, 55(3): 229-243.

[3] CHANG C I, Plaza A. A fast iterative algorithm for implementation of pixel purity index[J]., 2006, 3(1): 63-67.

[4] CHANG C I, Wu C C, Liu W, et al. A new growing method for simplex-based endmember extraction algorithm[J]., 2006, 44(10): 2804-2819.

[5] Nascimento J M P, Dias J M B. Vertex component analysis: A fast algorithm to unmix hyperspectral data[J]., 2005, 43(4): 898-910.

[6] Lopez S, Horstrand P, Callico G M, et al. A low-computational- complexity algorithm for hyperspectral endmember extraction: Modified vertex component analysis[J].,, 2012, 9(3): 502-506.

[7] Boardman J W. Geometric mixture analysis of imaging spectrometry data[C]//, 1994.'94,, Pasadena, CA, 1994: 2369-2371.

[8] 耿修瑞, 张霞, 陈正超, 等. 一种基于空间连续性的高光谱图像分类方法[J]. 红外与毫米波学报, 2004, 23(4): 299-302.

GENG Xiu rui, ZHANG Xia, CHEN Zhengchao, et al. Classification algorithm based on spatial continuity for hyperspectral image[J]., 2004, 23(4): 299-302.

[9] Clark R N, Swayze G A. Evolution in Imaging Spectroscopy Analysis and Sensor Signal-to-Noise: d P. An Examination of How Far We Have Come[C]//,, CA, 1996: 49-53.

[10] Tao X, Wang B, Zhang L. Orthogonal bases approach for the decomposition of mixed pixels in hyperspectral imagery[J].,, 2009, 6(2): 219-223.

[11] U.S Geological Survey Library. splib06b[EB/OL]. 2007, http://speclab. cr.usgs.gov/spectral.lib06b.

Endmember Extraction Algorithm Based on Hyperspectral Data Simplification

XU Jun1，SONG Kai1，LI Bo1，CAI Tijian1，WANG Cailing2

(1.,,330013,; 2.,’,’710065,)

This paper proposes a new algorithm which designs a suitable hypersphere in the feature space by utilizing the spatial information of the hyperspectral image in the feature space to separate the simplex vertices outside the hypersphere, then the data inside the hypersphere is excluded and only a small amount of data outside the hypersphere is involved in endmember extraction algorithm. Our analysis indicates that this method can greatly reduce the amount of computation of the endmember extraction algorithm and therefore can improve the operational speed. The final experimental results illustrate that the endmembers extracted from the simplified hyperspectral data by certain algorithms based on convex geometry have high precision and almost are identical to the endmembers extracted from the hyperspectral data before simplification by utilizing same algorithms.

hyperspectral remote sensing，endmember extraction，spatial information，hypersphere，hyperspectral unmixing

P237

A

1001-8891(2016)06-0481-05

2015-12-30；

2016-05-23.

徐君（1979-），男，博士，讲师，主要研究领域为光谱成像、光谱图像处理。E-mail：xjsdcq@163.com。

国家自然科学青年基金项目（41301382）；教育部人文社科青年基金项目（13YJCZH089）；江西省科技支撑项目（20151BBG70055）。