非制冷红外焦平面探测器噪声的频域分析

雷述宇，邵士靖，谭 果



非制冷红外焦平面探测器噪声的频域分析

雷述宇，邵士靖，谭 果

（北方广微科技有限公司，陕西 西安 710065）

传统3D噪声模型将噪声分解为8个部分，使复杂的噪声现象变得容易理解，然而这个模型没有准确的噪声分离方法和物理机理阐述。因此提出一种改进的探测器噪声分离和量化方法：噪声频域分析方法。这种方法将多帧噪声数据在空间和时间上分离为11个部分，并通过仿真实验分析各部分噪声对成像画面影响的强弱顺序，同时指出了每部分噪声的物理机理。噪声频域分析为红外探测器建立了一个完整的噪声模型，对理解红外探测器噪声特性、产生机理，及有针对性地进行噪声处理指明了方向。

非制冷焦平面；红外探测器；空间噪声；时间噪声；噪声模型

0 引言

近年来，随着红外成像技术的飞速发展，非制冷红外焦平面探测器（uncooled infrared focal plane array，uncooled-IRFPA）已经成为第三代低成本红外探测器[1]，具有体积小、灵敏度高、性能稳定等优点，应用领域从最初的科学研究、军事科学，扩展到医疗、工业、防火防灾等各个民用领域。然而，与制冷型探测器相比，非制冷探测器的噪声比较大，所以相应的最小可辨温差和噪声等效温差等关键指标不如制冷型探测器，阻碍了非制冷探测器的进一步推广和应用。因此，研究非制冷探测器的噪声特性和产生来源就显得特别重要。

对于红外探测器，画面上除了目标以外的一切信息都可以统称为噪声。如果目标是均匀的，比如黑体，那么画面上扣除平均值后，所有信息都是噪声。因此，研究噪声最方便的还是采用均匀目标下的成像画面，如无特别声明，本文研究的画面均为均匀目标（比如黑体）下的成像画面。噪声包括时间噪声和空间噪声2类。

时间噪声是指在不同的时刻，画面上探测器的输出与期望值之间的偏差。如果我们长时间地监测固定目标下的像元输出就能够发现这种在期望值附近的上下波动。

空间噪声又称固定图像噪声或者非均匀性噪声，是指由于工艺水平的限制，焦平面阵列上每一个像元对于均匀红外辐射的光电响应不完全一致，因而在图像上表现为空间噪声，严重地影响了成像质量[2-3]。遗憾的是，目前国内对于空间噪声的理解仍然存在不少误区。比如在国标GB/T17444-2013中，空间噪声的定义是：红外焦平面在均匀辐照条件下，各有效像元输出电压的均方根偏差[4]，计算公式如下：

FPN＝STD(o¢) (1)

式中：o'是除去死像元和过热像元后的焦平面像元电压输出。这个空间噪声的定义是基于探测器的输出电压，并未对成像画面的空间噪声做出定性或定量表述。在成像系统中，实时成像之前都要对探测器的输出电压做非均匀性校正[5]（non-uniformity correction，NUC），校正后的数据再通过显示设备转换成最后的画面信息[6]。因此，经过校正之后的非均匀性残留才会给画面带来空间噪声。要衡量实际探测器的成像质量，简单应用国标中空间噪声的定义是不合适的。

鉴于目前国内还没有统一的对成像画面时间噪声和空间噪声的定义和度量方法，提出了一种针对非均匀校正后噪声的分离和量化方法。通过频域分析，将噪声在时间和空间上分离为11个噪声分量，分析了各个噪声分量对成像的影响和各自的产生机制，更好地理解了噪声的本质，为提出更合适的算法和提高画面质量指明了方向。

1 红外焦平面噪声的传统分析方法

现在应用最多的传统噪声模型是三维噪声模型，是D¢Agostino和Webb在20世纪80年代提出的[7]，该模型按照时空关系将噪声分成8个部分，从空域和时域两个角度来分析噪声，促进了人们对噪声的理解和分析。

三维空间噪声模型的数学表达式如下：

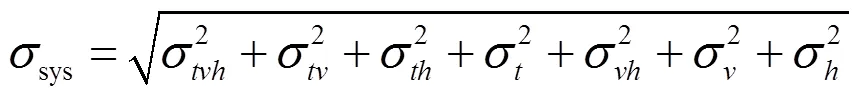
式中：下标是帧序，表示时间域；下标和分别表示二维空间域中的行序和列序，每个分量的具体含义如表1所示。

表1给出了8种噪声的描述，说明噪声产生的机理完全不同，存在形式和表现形式与光电系统的成像技术有关[8]。三维噪声模型将噪声分解为8个部分，比较全面地表征噪声源的特征，使复杂噪声现象变得容易理解。然而，这个噪声模型没有准确的分析方法，也没有准确地描述噪声的物理机制。为此，我们提出噪声频域分析方法，为红外探测器图像噪声建立一个具体而明确的噪声模型，以便能够更好地研究和理解不同噪声的机理，促进高效的降噪算法的开发。

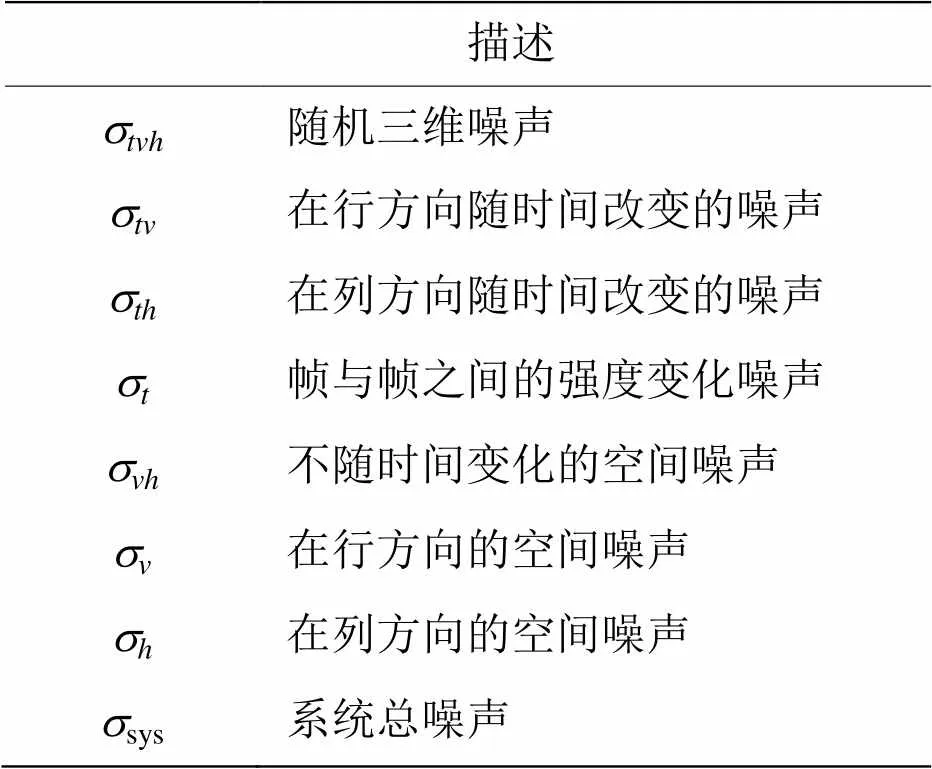
表1 三维噪声模型中的8种噪声

2 噪声频域分析方法

傅里叶变换是数字信号处理领域一种很重要的算法，傅里叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。根据该原理创立的傅里叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。傅里叶变换将原来难以处理的时域信号转换成了易于分析的频域信号（信号的频谱），可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅里叶逆变换将这些频域信号还原为时域信号。在本文中，我们将噪声在空间和时间上进行傅里叶变换，将噪声分离成11个部分。

2.1 二维（空间）离散傅里叶变换分离空间噪声

二维离散傅里叶变换傅里叶变换和逆变换如式(3)和(4)：

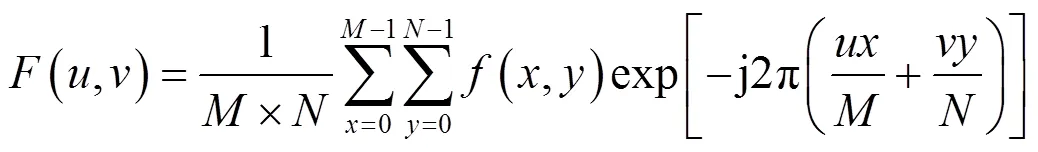
式中：＝0,1,2,…,－1；＝0,1,2,…,－1。

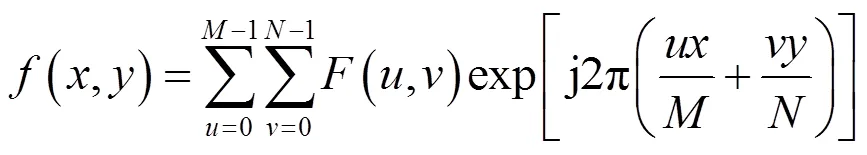
式中：＝0,1,2,…,－1；＝0,1,2,…,－1。

黑体红外画面数据的空间频率是表征画面变化剧烈程度的指标，是图像在平面空间上的梯度。而二维傅里叶变换是分析空间噪声频谱组成的有力工具，经过变换并将中心平移后，频谱数据的中心是直流分量；横轴上的频谱分量col是空间竖条纹；纵轴上的频谱分量row是空间横条纹；直流分量为中心，以一定频率（0.03倍行频和列频）为半径的圆内（或椭圆内）频谱分量lf是低频空间噪声；横轴和纵轴都大于一定频率（0.3倍行频和列频）的频谱分量hf为高频空间噪声；介于高频噪声和低频噪声之间的频谱分量block为斑块空间噪声。设图像中心坐标为(0,0)，各频谱分量的公式如下：

¢(,)＝fftshift[(,)] (5)

col＝{¢(0,)|≠0} (6)

row＝{¢(,0)|≠0} (7)

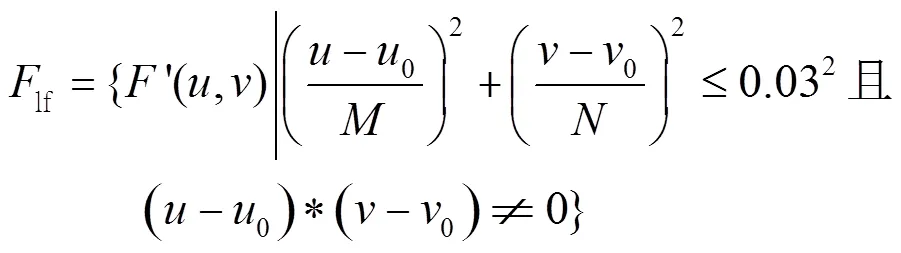
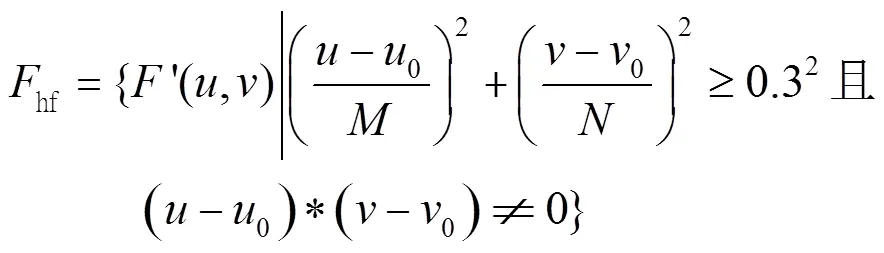
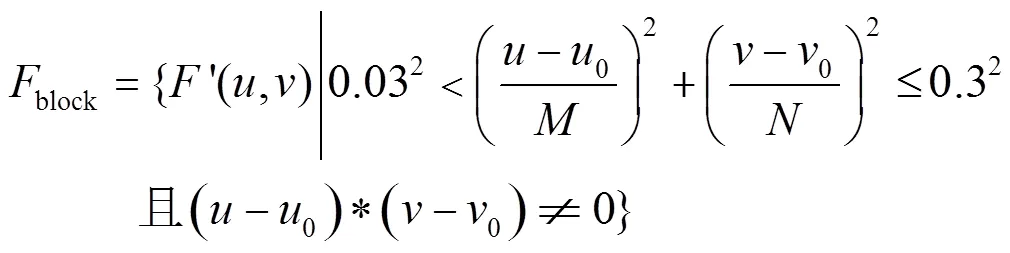
对频域数据经过数字滤波器处理即可得到上述各部分空间噪声的频谱分量。数字滤波器可以是理想滤波器、高斯滤波器以及其他FIR和IIR滤波器。本文采用的是理想滤波器。由于理想滤波器在边缘会出现振铃现象，我们将阵列往外扩展了10行和10列，然后只取中心384×288的阵列数据，从而避免振铃现象。后续我们将继续寻找更合适的滤波器。然后再依次对各部分空间噪声的频谱分量进行中心平移和傅里叶逆变换即可得到各部分空间噪声分量的图像（共6个图）。用公式表示如下：

col＝ifft2[ifftshift(col)] (11)

row＝ifft2[ifftshift(row)] (12)

lf＝ifft2[ifftshift(lf)] (13)

hf＝ifft2[ifftshift(hf)] (14)

block＝ifft2[ifftshift(block)] (15)

用一组实验数据来详细说明如何用二维傅里叶变换来分离空间噪声。该数据是384×288阵列探测器的多帧平均后的一组黑体成像数据，使用的软件是MATLAB2012。图1是黑体成像数据经过离散傅里叶变换前后的分布图，所用单位为LSB（1LSB＝0.3mV）。原始的空间噪声数据如图1(a)所示，该数据是14bit ADC的输出，1LSB为0.3mV，于是此时的电压大约在2.52V附近。图1(b)是经过中心平移后的频谱图，反映图像的梯度分布，其中频谱图的中心位置是直流成分。

在图1(b)的基础上，通过不同频域滤波器将噪声分离为6个部分：直流，低频，横条纹、竖条纹、斑块，以及高频噪声，噪声频域分析方法具体的设计思路如图2所示，图3和图4是空间噪声在频域的分布，所用单位为LSB。

图3(a)是低通滤波得到距离中心最近的低频噪声，图3(b)是频域纵轴上的横条纹噪声，图3(c)是频域横轴上的竖条纹噪声，图3(d)是带通滤波得到的斑块噪声，图3(e)是高通滤波得到的高频噪声。

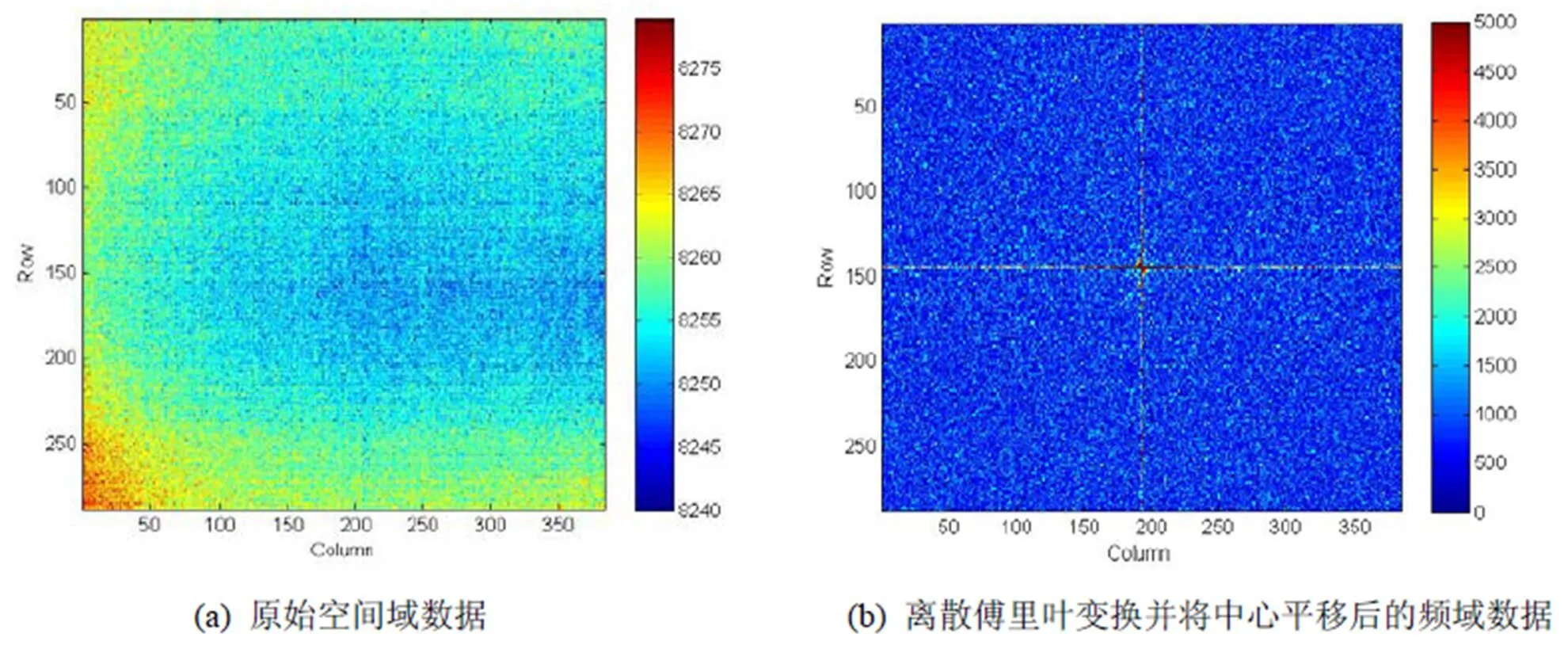
图1 离散傅里叶前后的数据分布

图2 空间噪声频域分析方法

图4是各个空间噪声频谱分量经过傅里叶逆变换后的空域分布图，图4(a)是去直流后得到的空域数据分布，低通滤波得到图4(b)的低频数据，与原始数据宏观趋势一致，中间低四周高的锅盖噪声；频域中横轴为竖条纹噪声，纵轴为横条纹噪声，实验结果如图4(c)和图4(d)所示；斑块噪声和高频噪声如图4(e)和图4(f)所示。

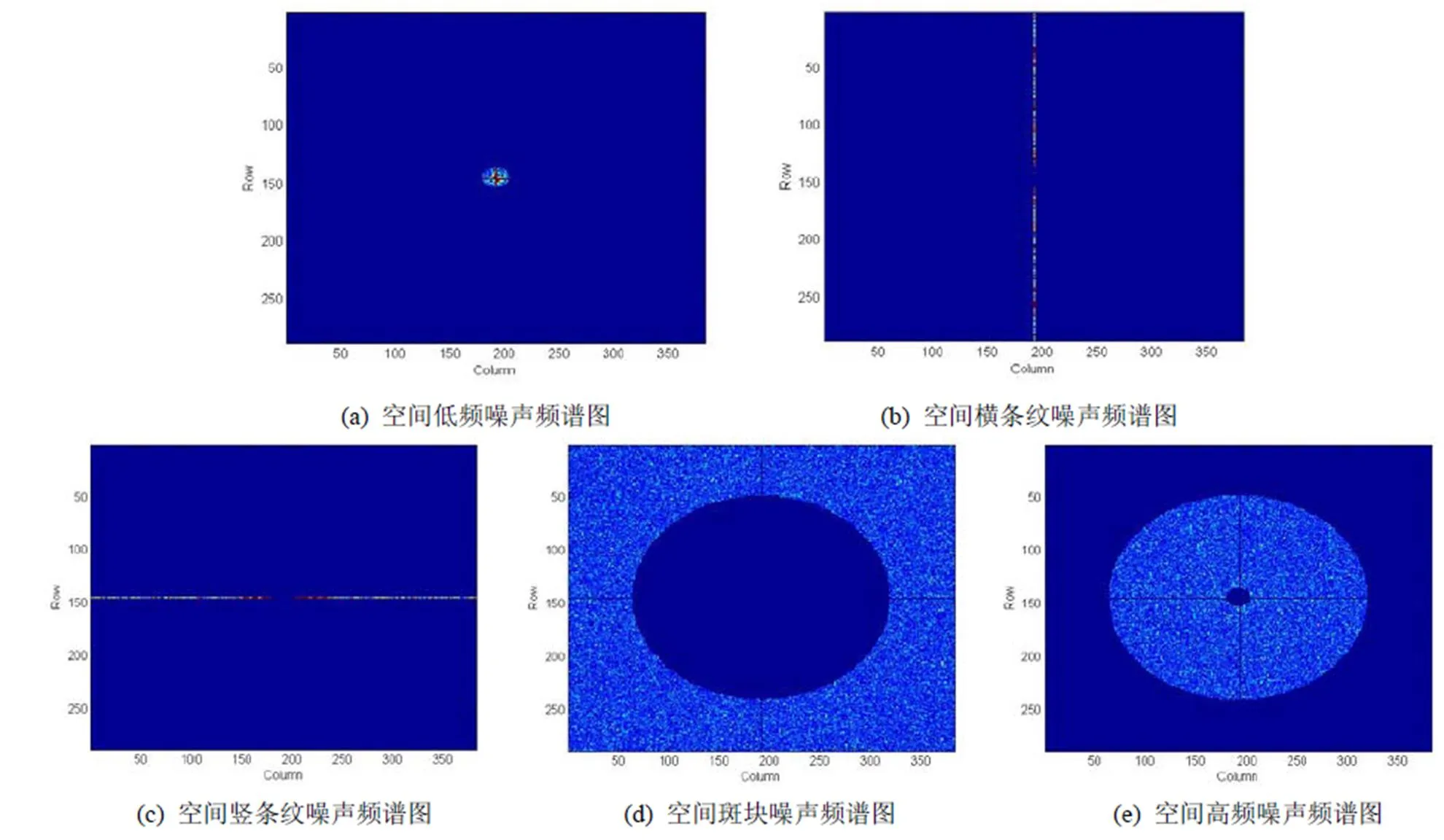
图3 不同空间噪声频谱图

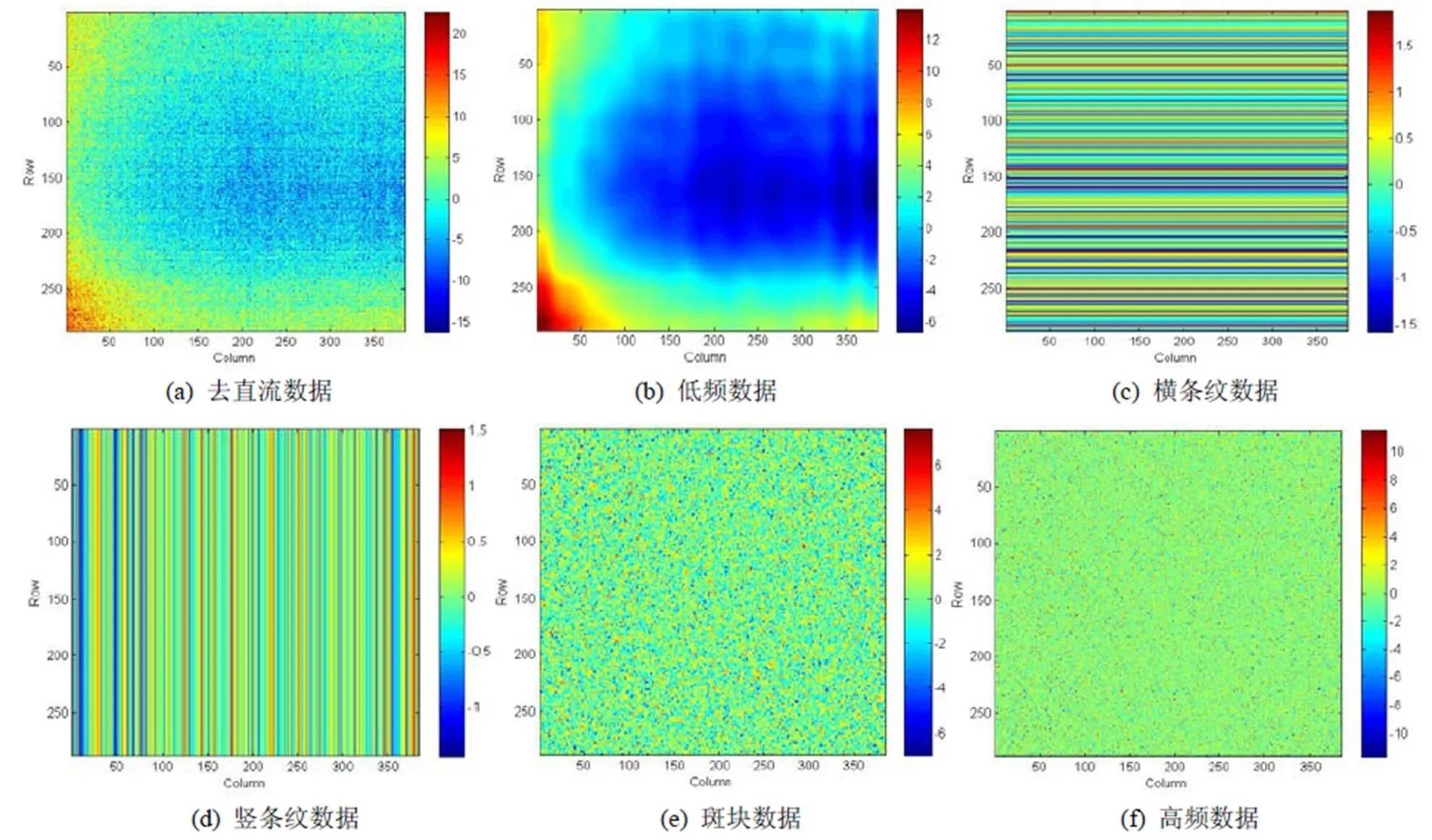
图4 空间噪声频域分析实验结果

2.2 一维（时间）离散傅里叶变换

一维（时间）离散傅里叶变换和逆变换如下：

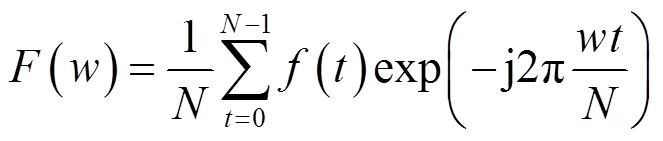
式中：＝0,1,2,…,－1。

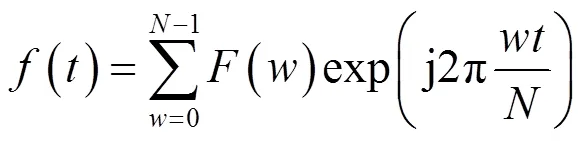
式中：＝0,1,2,…,－1。

上一节只是对单帧画面进行处理。严格地讲，对一帧画面进行处理只能得到空间噪声和时间噪声残留的总和。为了区分空间噪声和时间噪声，需要处理连续多帧画面。经过上一节处理，每帧噪声在空间上被分离为直流dc、低频lf、竖条纹col、横条纹row、斑块block和高频hf6个部分，画面总数扩展了6倍。再对各部分噪声在时间域上进行一维傅里叶变换和中心平移，取频率低于一定数值（如0.01倍帧频）的频谱分量经过逆变换后为空间噪声分量，剩余为时间噪声分量。对于像元(,)，其高频部分在多帧内组成了一个一维数组，将该数组进行傅里叶变换、低通滤波和逆变换以区分该像元处的空间高频噪声分量和时间高频噪声分量。为了简化，直接对时间域求平均得到空间噪声分量，剩余部分为时间噪声分量。以高频噪声为例，设总帧数为，简化的分离空间分量和时间分量的计算公式如下：

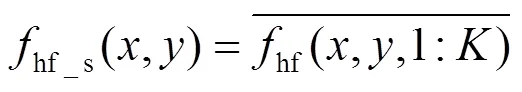
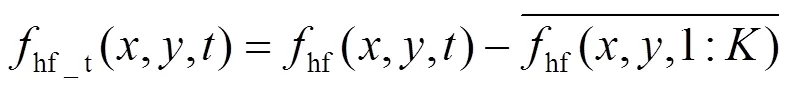
各部分的空间噪声分量求标准差表示这部分噪声的空间噪声；各个部分的时间噪声分量是三维数值，先对时域求标准差，然后各个像元求平均，得到该部分噪声的时间噪声。先将其分解为空间高频噪声分量（一帧画面）和时间高频噪声分量（多帧画面）。空间高频噪声分量求标准差代表空间高频噪声的大小。各像元的时间高频噪声分量求标准差，再求帧均值则代表时间高频噪声的大小。

这样，噪声被分离为11类噪声（直流量在多帧的均值求标准差为0，不算噪声，所以只有11类）。这11类噪声为直流噪声、时间和空间低频噪声、时间和空间横条纹噪声、时间和空间竖条纹噪声、时间和空间斑块噪声以及时间和空间高频噪声。11类噪声具体的计算公式如下：

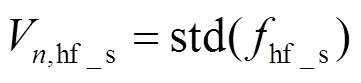
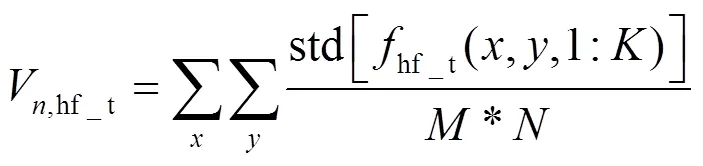
V,col_s＝std(col_s) (26)

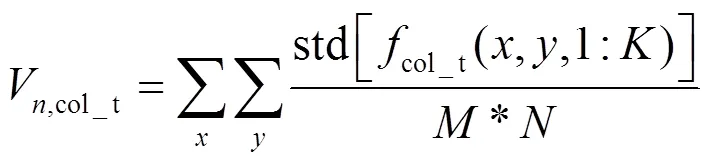
V,row_s＝std(row_s) (28)

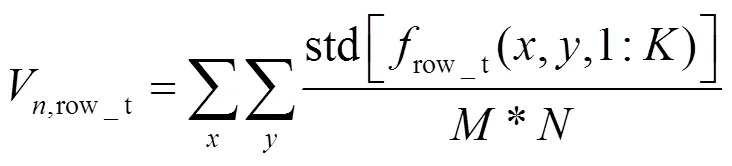
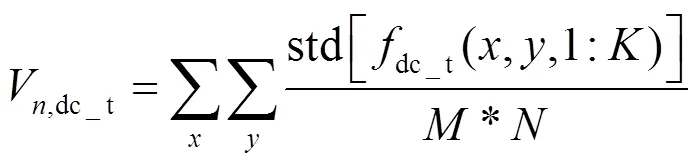
式(20)～(30)中，下标s表示空间，下标t代表时间。这样，可以逐一分析各部分对成像画面的影响。

现在再用一个例子来说明数据处理的方法和过程。实验数据为256帧384×288的黑体红外成像数据，每帧数据经过二维傅里叶变换分离6部分噪声，对每部分像元时间噪声进行一维傅里叶变换，结果如图5所示。图5(a)～图5(f)是6类时间噪声的时域分布，6类噪声经过一维离散傅里叶变换后的频域图如图5(g)～图5(l)。时间噪声的频域图中可以看到，直流时间噪声的低频分量是主导成分，其他5类噪声频谱较均匀，大体都是时间高斯白噪声。11类噪声的定量计算结果如表2所示。

3 分频后的噪声能量分布和它们分别对成像的影响

黑体红外成像数据分离的11类噪声对画面的影响不一定与噪声大小成正比，我们通过实验验证了这11类噪声对成像画面的影响。实验方法是在有四杠靶弱信号画面上叠加11类噪声，然后逐渐减去不同噪声，比较这11类噪声对成像画面的影响。实验结果灰度分布如图6所示。

图6(a)是有四杠靶弱信号的画面，图6(b)是图6(a)上叠加红外11类图像噪声，画面有大量噪声，四杠靶看不见；图6(c)是减去黑体时间高频噪声后的灰度分布，画面中颗粒感减弱，块状噪声明显；图6(d)是减黑体时间斑块噪声后灰度分布，画面颗粒噪声再次出现；图6(e)是减黑体空间高频噪声后的灰度分布，四杠靶隐约可见，画面还有斑驳感；图6(f)是减黑体空间斑块噪声后的灰度分布，四杠靶可见，画面横竖条纹噪声明显；在经过大量实验验证，横竖条纹对成像画面影响从强到弱的顺序是：时间横条纹、时间竖条纹、空间竖条纹和空间横条纹，成像画面分别如图6(g)～6(j)所示；再之后对画面影响的是空间低频噪声和时间低频噪声。

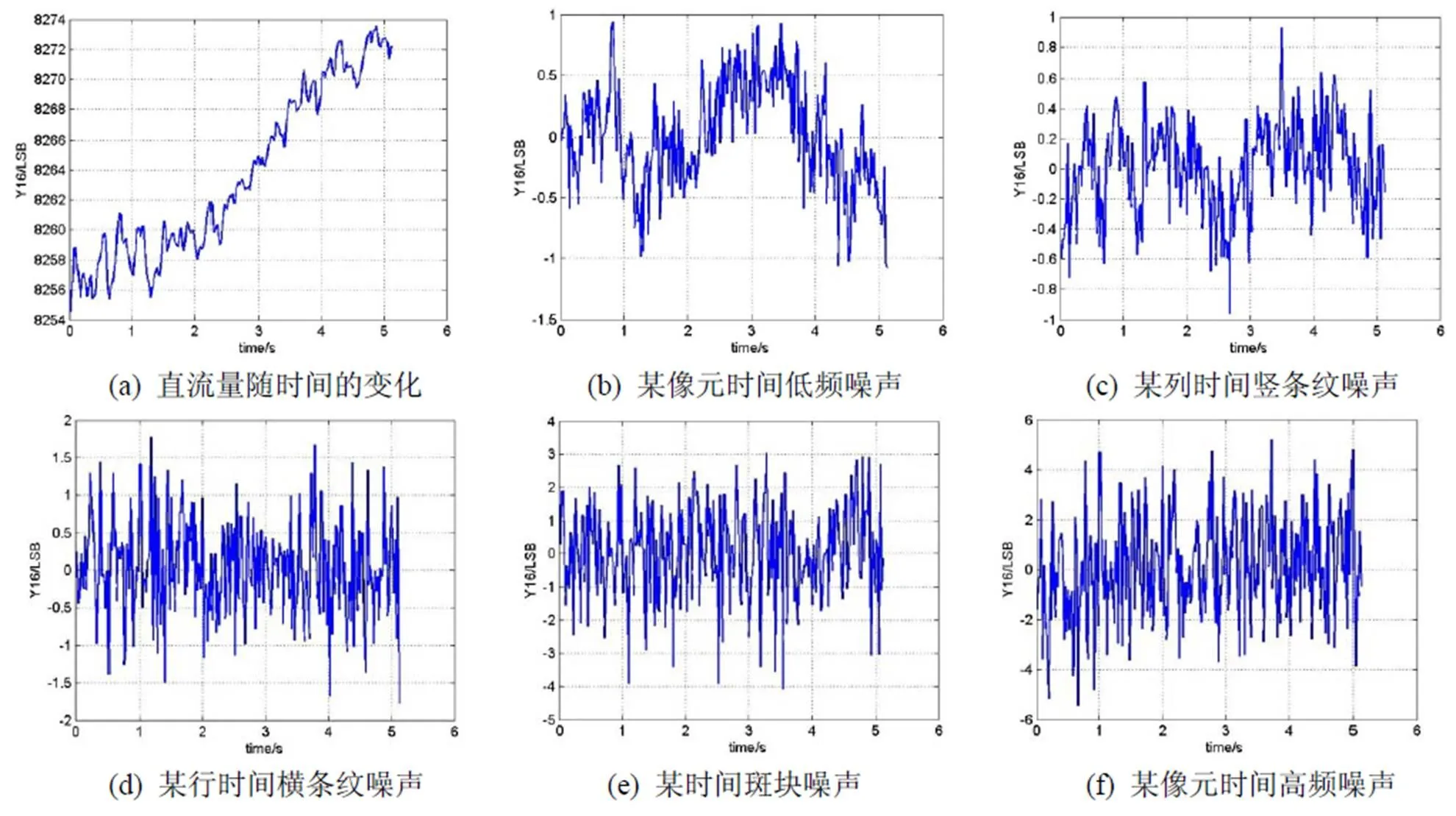
表2 11类噪声的计算结果（1 LSB＝0.3 mV）

通过分析可以说明，噪声对信号影响从强到弱的顺序是：时间高频噪声、时间斑块噪声、空间高频噪声、空间斑块噪声、时间横条纹噪声、时间竖条纹噪声、空间竖条纹噪声、空间横条纹噪声、空间低频噪声、时间低频噪声，最后是帧时间噪声。实验数据是基于我们一款384×288的探测器的实际测试结果，虽不代表所有探测器的性能，但是不失一般性。

4 分离后的典型噪声的物理机理

噪声频域分析方法能够将噪声在时间和空间上分为11类，针对这11类噪声进行物理原因的分析，以便优化探测器的噪声性能。

空间噪声可分为斑块噪声、高频噪声、竖条纹噪声、横条纹噪声和低频噪声几类：

1）斑块和高频噪声主要是由阵列内像元膜层存在非均匀性，使得各像元红外吸收率、阻值、电阻温度系数、热导、热容等参数存在差异，导致的像元级信号输出差异。

2）竖条纹噪声是由列级盲像元阻值的非均匀和列级读出电路的寄生电容、电阻的差异等因素引起信号放大倍数的差异导致。

3）横条纹噪声是由行级盲像元阻值的非均匀性引起的。

4）空间低频噪声存在2个产生机理：①是工艺不均匀性，实际的生产工艺是有局限性的，导致感光像元在整个阵列内存在宏观趋势，即使经过了非均匀性校正，也不能完全消除；②是镜头引起的锅盖效应，这是因为镜头会导致探测器的中心像元和边缘像元的外辐射和内辐射立体角不同，即使经过了A矩阵校正，也不能完全消除。

时间噪声分为直流噪声、横条纹噪声、竖条纹噪声、低频噪声、斑块噪声和高频噪声几类：

1）横条纹噪声主要来自探测器工作的行级共用偏压的噪声和行级公用的盲像元电阻的热噪声和闪烁噪声。

2）竖条纹噪声主要来自列级共用的盲像元电阻的闪烁噪声以及列级读出电路的闪烁噪声。

3）时间高频噪声和时间斑块噪声主要来自探测器敏感像元和盲像元的热噪声和闪烁噪声。

4）探测器衬底温度随时间的变化会带来时间低频噪声和直流噪声。

5 结论

针对均匀目标下的红外成像画面的噪声，基于传统噪声3D噪声模型，开发了噪声频域分析方法，将探测器噪声在时间和空间上细分为11类并给出了各类噪声大小的计算方法。然后，通过实验数据分析和成像画面分析，计算分离后噪声的能量及其对成像画面的影响，并给出每部分噪声的物理机制，为降低图像噪声指明了优化方向。频域分析方法是一种比较常用的信号处理方式，论文中实验结果表明，噪声频域分析方法能够更加精准的分离噪声，更加准确地体现噪声的物理机理。噪声频域分析为红外探测器图像噪声建立一个完整的噪声模型，能够更好的理解噪声的本质，能够更好的提出适合的降噪算法，提高成像画面质量。

[1] 史衍丽. 第三代红外探测器的发展与选择[J]. 红外技术, 2013, 35(1): 1-8.

SHI Yanli. Choice and development of the third-generation infrared detectors[J]., 2013, 35(1): 1-8.

[2] 张爽, 周慧鑫, 牛肖雪, 等. 基于非局部均值滤波与时域高通滤波的非均匀性校正算法[J]. 光子学报, 2014, 43(1): 153-156.

ZHANG Shuang, ZHOU Huixin, NIU Xiaoxue, et al. Temporal high-pass filter nonuniformity correction algorithm based on non-local means filter for infrared focal plane array[J]., 2014, 43(1): 153-156.

[3] 刘永进, 朱红, 赵亦工. 基于粒子滤波的红外焦平面阵列非均匀性校正算法[J]. 红外与激光工程, 2008, 37(6): 945-950.

LIU Yongjin, ZHU Hong, ZHAO Yigong. Nonuniformity correction algorithm of infrared focal arrays based on particle filters[J]., 2008, 37(6): 945-950.

[4] 中国国家标准化管理委员会. 红外焦平面阵列参数测试方法: GB/T17444-2013[S]. 北京: 中国标准出版社, 2013.

Standardization Administration of the People's Republic of China. Method of measuring parameter of infrared focal arrays: GB/T17444-2013[S]. Beijing: China Standard Press, 2013.

[5] 曹扬, 金伟其, 刘崇亮, 等. 红外焦平面阵列的自适应非均匀性校正及硬件实现[J]. 光学精密工程, 2011, 19(12): 2985-2990.

CAO Yang, JIN Weiqi, Liu Chongliang, et al. Adaptive nonuniformity correction and hardware implementation of IRFPA[J]., 2011, 19(12): 2985-2990.

[6] 王晖. 基于三次多项式拟合的快速非均匀校正算法[J]. 航空兵器, 2008(4): 11-14.

WANG Hui. Fast uniformity correction algorithm based on cubic polynomial fitting[J]., 2008(4): 11-14.

[7] D'Agostino J A, Wedd C M. Three-dimensional analysis framework and measurement methodology for imaging system noise[C]//, 1991, 1488:110-121.

[8] 张建奇, 王晓蕊. 光电成像系统建模及性能评估理论[M]. 西安: 西安电子科技大学出版社, 2010.

ZHANG Jianqi, WANG Xiaorui.[M]. Xi’an: Xidian University Press, 2010.

The Frequency Analysis Method of Noise in Uncooled IRFPA Detector

LEI Shuyu，SHAO Shijing，TAN Guo

（,’710065,）

Traditional 3D noise model divides the noise into 8 parts, enabling the noise being easily understood. However, this model does not provide an accurate method to divide the noise parts and explanation of the noise generating mechanism. An optimized way to divide and quantize the detector noise was proposed by frequency analysis of noise. This noise analysis method divides noise into 11 parts by means of FFT, and then calculates the percent of each part in overall noise and analyzes the effect of each part on the image quality, and lastly explains the noise generating mechanism of each part of noise. The frequency analysis method provides a complete noise model for IR detectors and is proven to be an effective IR signal processing way.

uncooled IRFPA，IR detector，FPN，temporal noise，noise model

TN215

A

1001-8891(2016)06-0449-08

2016-06-01；

2016-06-13.

雷述宇（1972-），男，博士，主要从事非制冷红外探测器研究。E-mail：shuyu.lei@gwic.com.cn。