基于协方差描述子稀疏表示的前视红外建筑物目标跟踪锁定

杨春伟，王仕成，廖守亿，刘华平



基于协方差描述子稀疏表示的前视红外建筑物目标跟踪锁定

杨春伟1,2，王仕成1，廖守亿1，刘华平2

（1. 第二炮兵工程大学 精确制导仿真技术实验室，陕西 西安 710025；2. 清华大学 计算机科学与技术系，北京 100084）

作为前视红外成像末制导的关键部分，红外目标跟踪是一个极具挑战性的课题。本文针对前视红外建筑物目标，提出了一种基于协方差描述子稀疏表示的红外目标跟踪框架。首先，提取红外建筑物目标的协方差描述子特征；其次，由于协方差描述子属于黎曼空间，采用log-Euclidean变换将其转换到欧式空间；最后，在粒子滤波的理论框架基础上，采用目标在字典中的稀疏表示作为观测模型，对红外建筑物目标进行表示，通过贝叶斯状态推理框架进行目标跟踪。对前视红外建筑物目标的跟踪实验表明，该方法在跟踪准确度及鲁棒性方面体现出了优良的特性。

红外建筑物；目标跟踪锁定；稀疏表示；协方差描述子；仿射变换

0 引言

复杂背景下的地面红外目标跟踪锁定能够为红外成像末制导提供重要的技术支撑。与可见光图像相比，红外图像信噪比低，易受背景杂波的干扰。同时，在前视红外成像制导系统中，由于成像系统的自我运动以及天气等原因，使得前视红外目标的跟踪锁定成为一个极具挑战性的问题[1-2]。

与模板匹配法、光流法以及卡尔曼滤波等经典的红外目标跟踪方法相比，粒子滤波算法在处理非线性和非高斯情况下的动态系统状态估计问题取得了很好的效果。粒子滤波以蒙特卡罗随机模拟理论为基础，它将系统状态的后验分布采用一组随机样本的加权来表示，新的状态分布则通过这些随机样本的贝叶斯迭代进化生成。

最近几年，稀疏表示在模式识别以及计算机视觉领域受到了越来越多的关注。文献[3-4]将稀疏表示引入目标跟踪领域，跟踪问题被看作粒子滤波理论框架下的稀疏近似问题，遮挡、噪声等问题通过平凡模板来解决，而待跟踪目标通过模板空间的稀疏表示来近似，并通过非负约束减少误匹配结果，最终的跟踪结果通过投影误差来确定。文献[5]在上述成果基础上，指出将平凡系数的L1约束改为L2约束，能够更好地表征平凡系数的能量，从而可以更加有效地处理遮挡，背景噪声等问题，同时采用APG（accelerated proximal gradient）算法提高了文献[3-4]中跟踪算法的实时性。文献[6]将该理论框架引入红外目标跟踪领域，取得了良好的跟踪效果。

另一方面，文献[7]第一次将协方差描述子引入目标跟踪领域，文献[8-9]将协方差描述子与稀疏表示相结合，在粒子滤波理论框架下设计了跟踪算法。但文献[8-9]中的算法采用L1约束处理平凡系数。

基于以上成果，本文将协方差描述子引入前视红外建筑物目标跟踪锁定领域，提出了基于协方差描述子稀疏表示的前视红外建筑物目标跟踪锁定算法。该方法与上述算法主要有两点不同：

1）采用协方差描述子作为目标特征，与基于灰度特征的目标跟踪算法[3-5]相比，无需对系数进行非负约束。

2）与文献[8-9]相比，该方法受文献[5]启发，对平凡系数引入L2约束。

1 方法综述

图1所示为基于协方差描述子稀疏表示的前视红外建筑物目标跟踪锁定算法流程，算法总体上采用稀疏表示与粒子滤波结合的思想，主要分为以下几步：第一，根据前一帧的检测结果或者通过人工标注确定待跟踪目标，并根据待跟踪目标位置采用小幅扰动的方式建立字典；第二，基于仿射变换，根据状态转移概率密度采样，得到当前帧的粒子集；第三，基于第一步建立的字典，对粒子集进行稀疏表示，并计算每个粒子的权值；第四，根据粒子权值，确定跟踪结果并锁定，并进行字典更新与粒子重采样。

2 协方差描述子提取与映射

2.1 协方差描述子

对于红外图像块的每个像元，我们首先计算式(1)所示的维（此处＝5）特征向量：

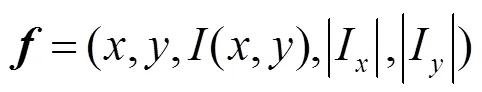
式中：，，(,)分别为像元坐标以及坐标为(,)处的像元的灰度值，后二者为水平和垂直方向的一阶梯度值。

令为红外图像块的像元个数，为特征集{}，＝1, 2, …,的均值，那么红外图像块可以通过式(2)所示的×协方差描述子来表示：

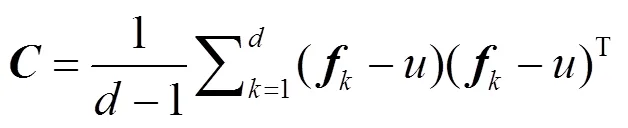
该协方差描述子融合了图像像元的位置，灰度值以及一阶梯度值之间的相关关系，具有以下优点[10]：首先，协方差描述子可以融合不同特征，其对角线元素表征了特征之间的变化，非对角元素表征了特征之间的相关性；第二，协方差计算减轻了噪声对于单个样本的影响；第三，协方差描述子具有一定的尺度旋转不变性。

2.2 协方差描述子的快速计算

为了能够快速计算目标的协方差描述子，我们可以采用积分图像的方法[11]。具体地，式(2)可表示为：

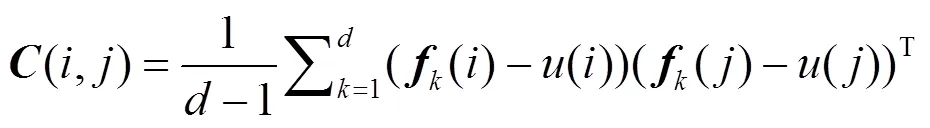
Fig.1 FLIR building tracking flowchart

展开后可得：

从式(4)可以看出，为了计算目标的协方差描述子，需要计算每一维特征之和以及任意两维特征的乘积之和。因此针对每维特征()以及任意两维特征乘积()()，建立＋2幅积分图像。

令为积分图像的××的张量（，分别为红外图像块的长宽值）：

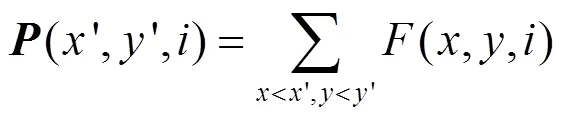
为二阶积分图像的×××张量：

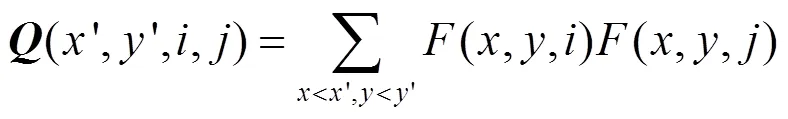
令：

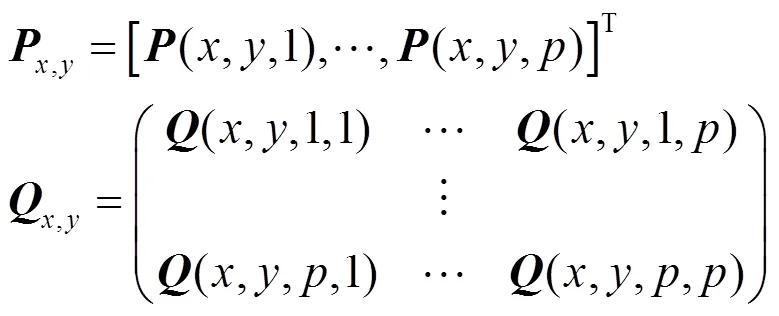
此处，,y为对称矩阵，式(7)的计算量为＋(＋2)/2，因此积分图像的计算复杂度为(2)。这样，红外图像块的协方差特征可通过下式计算：

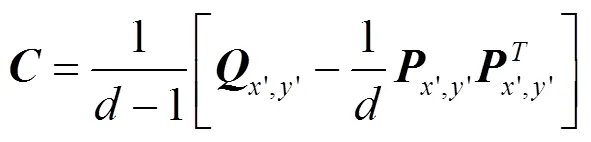
式中：¢，¢为目标的右下角坐标值。这样，建立积分图像之后，协方差描述子的计算复杂度为(2)。

2.3 欧式映射

协方差描述子包含于对称正定矩阵形成的流形中，其统计特性可以通过黎曼几何近似计算[12]。

对于对称正定矩阵，矩阵的指数以及对数运算为基本操作[13]。给定×协方差描述子，通过奇异值分解（＝）得到正交矩阵以及对角矩阵＝Diag(1,2, …,)，其中{}＝1, 2,…,k为的特征值。那么，的指数以及对数运算分别定义为：

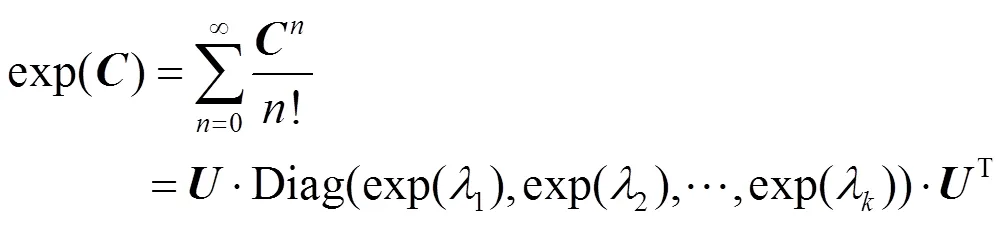
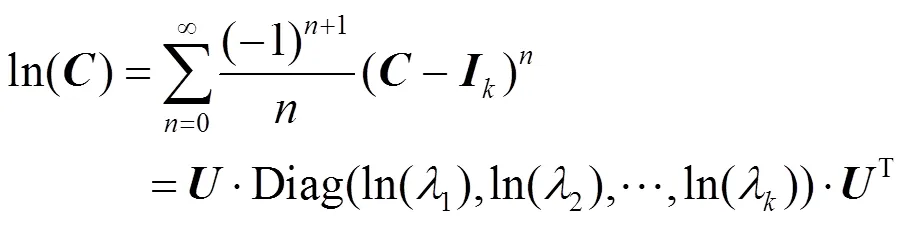
式中：为×单位矩阵

这样，协方差描述子可通过log-Euclidean映射转换为列向量，即：

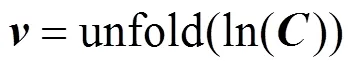
式中：unfold(×)将矩阵转化为向量。

3 粒子滤波

粒子滤波是一种估计动态系统状态变量后验概率分布的贝叶斯序贯重要性采样技术，它提供了非线性非高斯情况下用于状态变量后验概率密度函数估计以及繁殖的框架。粒子滤波包含两个基本步骤：预测和更新。

令x为红外建筑物目标在第帧的仿射运动参数，令帧之前的观测值为1:t－1＝{1,2,…,y－1}，那么x的预测分布(x|1:t－1)可通过下式递归计算：

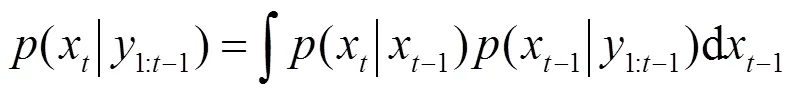
在第帧，基于观测值y，状态向量根据下式的贝叶斯准则进行更新：

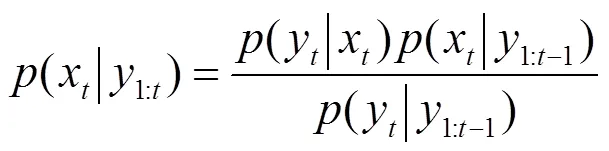
其中，(y|x)表示观测似然度函数。

但是很多情况下，式(12)(13)无法得到解析解，因此只能通过近似方法求解。而粒子滤波则是一类行之有效的逼近方法，其主要思想是利用个随机产生的粒子{}＝1,…, N（对应的权值为）加权和对后验概率密度进行表示。候选粒子通过重要性分布(x|1:t－1,1:t)获得，粒子的权重根据下式更新：

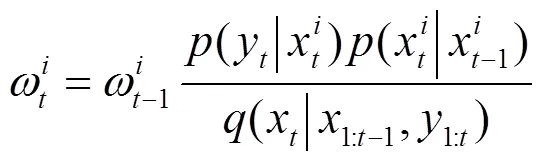
为了避免粒子退化，粒子根据重要性权重重采样生成一系列相同权重的粒子。

在跟踪过程中，我们采用仿射变换描述相邻帧之间红外建筑物目标的运动。状态变量x由6个仿射变换参数决定，即：x＝(1,2,3,4,1,2)，其中(1,2,3,4)为形变参数，(1,2)为位移参数。通过仿射变换，目标以及粒子可以进行一定的大小形状变换。状态转移分布(x|x－1)采用高斯分布模型，观测似然度函数(y|x)反映了粒子与目标模板之间的相似度，可以通过下面的稀疏表示重建误差来表示。

4 稀疏表示

假设跟踪过程中，红外建筑物目标位于低维子空间。给定目标模板集＝[1,2, …,v]ÎR×，包含个目标模板v∈R（=×为目标模板的协方差描述子在欧式空间的映射特征向量），那么跟踪结果可近似表示为目标模板集的线性组合，即：

≈＝11＋22＋…a v(15)

式中：＝[1,2, …,a]为稀疏系数向量。

由于实际跟踪过程中会不可避免地出现噪声、遮挡等情况，我们通过建立平凡模板＝[1,2, …,i]∈R×并转化为列向量来解决这个问题，因此式(9)可转换为：

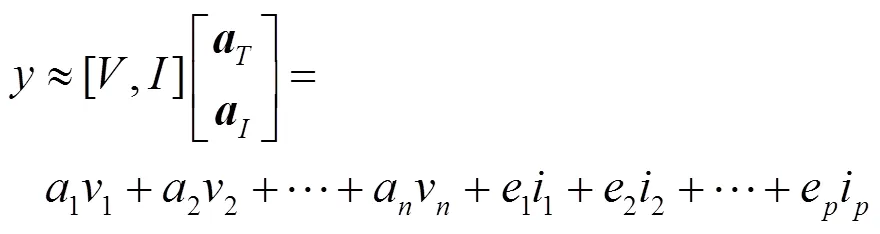
式中：平凡模板ii∈Rm仅有一个非零值；aI＝[e1, e2,…, en]为平凡系数向量。a＝[aT, aI]T为系数矩阵，D＝[V, I]为字典，具体构造过程如图2所示，首先目标模板通过对初始确定的待跟踪目标框的中心位置加入随机扰动得到，然后提取每个目标模板的协方差描述子，通过log-Euclidean映射将其映射到欧式空间形成特征向量最终得到目标模板集，将目标模板集与平凡模板集进行级联得到最终的字典。

在当前帧，红外目标在字典中的稀疏表示可以通过求解下式所示的L1范数最小化得到[6]：

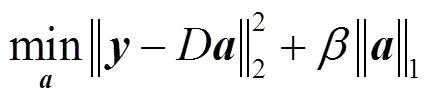
然而，文献[5]指出，若候选区域为正确的跟踪结果，那么当前帧的目标可以通过目标模板的稀疏线性组合很好地近似，这样，对应的平凡系数的能量（L2范数）会很小。相反，当候选区域收到背景噪声污染或被遮挡时，当前帧的目标若通过目标模板的稀疏线性组合表示，将会产生很大的误差，而这大部分误差将由平凡模板来弥补，导致平凡系数能量很大。因此，式(17)可转换为如下的最小化模型：

式中：和为正则化参数，分别控制稀疏系数和平凡系数的稀疏度。

式(18)可通过APG方法来求解[14-15]。采用样本与稀疏表示之间的残差作为相似性度量即目标的观测概率模型为：

式中：为控制参数；为样本与稀疏表示之间的残差。

对于模板更新，分为两部分来进行处理，即固定模板和其他模板。由于固定模板是通过人工标注或检测过程得到的结果，因此对目标具有很好的代表性，该模板自始至终都不变；而其他模板是通过对固定模板中心小范围扰动几个像素产生的，因此需要进行更新，具体策略如下：计算当前帧的目标跟踪结果与其他模板之间的角度，当大于某一阈值，则将当前跟踪结果替换其他模板中最不重要的模板，具体步骤见文献[3]。

5 实验结果分析

5.1 实验数据及基准算法

为了更好地测试本文提出算法（Cov_L1_L2）的优越性，选择两种算法作为基准算法进行对比试验：基于分块协方差的L1稀疏跟踪（Block_L1）算法[7]，基于log-euclidean黎曼空间稀疏表示（Cov_L1）的跟踪算法[8]。Block_L1算法对目标分块后提取每块的协方差描述子并转换到欧式空间进行串联实现目标的建模，而Cov_L1算法直接提取目标的协方差描述子后转换到欧式空间对目标进行建模，二者皆采用L1稀疏对残差进行建模。以上算法采用的都是粒子滤波跟踪的框架，且采用统一的目标运动模型。因此，本文算法与基准算法的区别有两点：一是特征提取方式的差异；二是对平凡系数处理的差异。测试红外视频采用图3所示的机载挂飞数据，分为白昼和夜间两个场景，每个场景各包含200帧红外视频序列，跟踪目标为在不同场景下的两栋建筑物（图中矩形框标注）。

图3 前视红外建筑物图像视频序列示例（白昼和夜间）

5.2 定性比较

图4、图5所示分别为本文算法与对比算法在白昼和夜间两个场景下的红外建筑物跟踪结果。从整体上看，本文提出的跟踪算法取得了良好的跟踪效果，明显优于基准算法。图4(a)中，在第5帧，红外视频图像出现了一定的抖动，两种基准算法的跟踪结果出现了漂移，而本文提出的算法跟踪一直比较稳健，随后Block_L1和cov_L1跟踪算法已无法跟踪目标，而cov_L1_L2虽然出现了一定的漂移，但是很快又重新捕获到了红外建筑物目标；至于图4(b)，两种基准算法自第5帧便出现了较大的偏移。从图5所示夜间场景下的红外建筑物跟踪结果同样可以看出，本文提出的cov_L1_L2跟踪算法与两种基准算法相比，针对红外目标出现的抖动现象，具有更加优良的鲁棒特性。

图4 白昼场景下两栋建筑物的跟踪结果

图5 夜间场景下两栋建筑物的跟踪结果

Fig.5 Tracking results of two buildings at night

5.3 定量比较

为了定量评估上述算法在不同场景下的跟踪效果，我们采用中心误差与重叠度[16]两个指标作为评估依据。计算机配置为3.0GHz的Intel Core i5 CPU，4G RAM，测试环境为MATLAB 2010b。中心误差指的是实际跟踪目标的中心位置与目标真实中心位置之间的欧氏距离，而平均中心误差则用来评估算法的整体跟踪效果。对于重叠度，令实际跟踪目标边界框为t，真实目标的边界框为a。那么重叠度定义为＝|t∩a|/|t∪a|，其中∩与∪分别为t和a的交集与并集区域。

图6、图7所示分别为两个建筑物目标在白昼和夜间两种场景下的跟踪中心误差曲线和跟踪目标重叠度曲线，表1所示为对应的平均跟踪误差（Average tracking error，ATE）以及帧频（Frame fre- quency）。由于基准算法在跟踪过程中出现了大量的失帧现象，从而导致平均跟踪误差以及重叠度都很差。从以上指标不难看出，本文所提的算法在前是红外建筑物目标的跟踪过程中尽管出现偶尔的失帧，但是能够很快地重新捕捉到目标，从准确度和鲁棒性上都要明显优于基准算法。但是由于本文算法引入L2约束，导致实时性有所降低。

6 结论

本文针对前视红外建筑物目标跟踪锁定问题，采用目标的协方差描述子作为特征，基于稀疏编码理论和粒子滤波框架，提出了一种基于协方差描述子稀疏表示的前视红外建筑物目标跟踪锁定算法。采用机载挂飞数据对算法进行测试，取得了良好的跟踪效果。但从实验结果看出，虽然该算法在准确性和鲁棒性上优于基准算法，但是在大扰动的情况下仍然出现了偶尔的失帧现象，后续工作将针对这一现象寻求更好的解决办法。

图6 不同场景下的前是红外建筑物目标跟踪中心误差

图7 不同场景下的前视红外建筑物目标跟踪重叠度

表1 算法平均跟踪误差

[1] HUANG Qiao, YANG Jie. A multistage target tracker in IR image sequences[J]., 2014, 68: 122-128.

[2] 张学峰.复杂地物背景下红外弱小目标跟踪算法[J].红外技术, 2015, 37(8):659-663.

ZHANG Xue-feng.Tracking of dim infrared target in complex background[J].,2015,37(8):659-663.

[3] XUE Mei, LING Haibin. Robust visual tracking using L1 minimization[C]//12, 2009: 1436-1443.

[4] XUE Mei, LING Haibin. Robust visual tracking and vehicle classification via sparse representation[J]//, 2011, 333(11): 2259-2272.

[5] BAO Chenglong, WU Yi, LING Haibin, et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]//, 2012: 1830-1837.

[6] 唐峥远, 赵佳佳, 杨杰, 等. 基于稀疏表示模型的红外目标跟踪算法[J]. 红外与激光工程, 2012, 41(5): 1389-1395.

TANG Zhengyuan, ZHAO Jiajia, YANG Jie, et al. Infrared target tracking algorithm based on sparserepresentation model[J]., 2012, 41(5): 1389-1395.

[7] PORIKLI Fatih, TUZEL Oncel, MEER Peter. Covariance tracking using model update based on lie algebra[C]//, 2006, 1: 728-735.

[8] ZHANG Xiaoqin, LI Wei, HU Weiming, et al. Block covariance based L1 tracker with a subtle template dictionary[J]., 2013, 46: 175-1761.

[9] WU Yi, LING Haibin, Blasch Erik, et al. Visual tracking based on log-Euclidean Riemannian sparse representation[C]//, 2011: 738-747.

[10] ZHANG Xiaoqin, LI Wei, HU Weiming, et al. Block covariance based L1 tracker with a subtle template dictionary[J]., 2013, 46: 1750-1761.

[11] TUZEL Oncel,PORIKLI Faith, MEER Peter. Region covariance: a fast descriptor for detection and classification[C]//, 2006: 589-600.

[12] LIN Tong, ZHA Hongbin. Riemannian manifold learning[J]., 2008, 30(5): 796-809.

[13] HU Weiming, LI Xi, LUO Wenhan, et al. Single and multiple object tracking using log-Euclidean Riemannian subspace and block -division appearance model[J]., 2012, 34(12): 2420-2440.

[14] LIN Zhouchen, Arvind Ganesh, John Wright, et al. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix[C]//, 2009: 1-18.

[15] GAO Chengqiang, MENG Deyu, YANG Yi, et al. Infrared patch-image model for small target detection in a single image[J]., 2013, 22(12): 4996-5009.

[16] WU Yi, LIM Jongwoo, YANG Ming-Hsuan. Online object tracking: a benchmark[C]//, 2013: 625-632013.

Forward-looking-infrared Building Object Tracking Based on Sparse Representation of Covariance Descriptor

YANG Chunwei1,2，WANG Shicheng1，LIAO Shouyi1，LIU Huaping2

(1.,¢710025,; 2.,,100084,)

As the key component of forward-looking-infrared(FLIR) image terminal guidance, infrared object tracking is a challenging task. In this paper, a FLIR building object tracking framework based on sparse representation of covariance descriptor(Cov) is proposed. First, the Cov of FLIR building is extracted and then transformed to Euclidean space due to the reason that Cov lies in Riemannian space. Then, based on particle filter theory, the observation model of object is represented through sparse representation of template dictionary, and object tracking is continued by using a Bayesian state inference framework. Experiments on FLIR building object show that the proposed method obtains effectiveness in tracking accuracy and robustness.

infrared building，object tracking，sparse representation，covariance descriptor，affine transformation

TP391

A

1001-8891(2016)05-0389-07

2015-12-28；

2016-01-04.

杨春伟（1986-），男，山东高密人，博士研究生，研究方向为“红外目标的检测与识别”。E-mail：yangchunwei081129@163.com。