行人过街信号控制路口交通噪声预测模型*

李 锋 蔡 铭

(1.广东技术师范学院汽车学院，广东 广州 510665；2.中山大学工学院，广东省智能交通系统重点实验室，广东 广州 510006)

城市交通噪声污染是影响人们生活和工作的重要环境问题之一。对道路交通噪声的预测是科学防治交通噪声的重要基础工作。道路交通噪声预测模型是计算和评估交通噪声污染程度的主要工具。长期以来，国内外学者在道路交通噪声预测方面做了大量的研究工作，并建立了各种有效的交通噪声预测模型[1-5]。早期的大部分模型均是在车辆匀速行驶的假设条件下建立起来，在车辆速度变化不大的道路上已达到了较高的预测准确度，但直接应用在道路交叉口等车辆速度变化较大的局部路段仍有一定误差。因此，越来越多的学者开始关注车辆加、减速频繁的局部路段的交通噪声预测模型和噪声变化规律。如林郁山等[6]、蔡铭等[7]考虑车辆加、减速的影响，采用实验方法建立了车辆噪声源排放模型；MAKAREWICZ等[8-10]针对车速限制和减速带等因素的影响，建立了间断交通流交通噪声预测模型；王波等[11]、常玉林等[12]、王超等[13]、ABO QUDAIS等[14]分析了道路交叉口交通流的特点，提出了信号控制十字交叉口交通噪声预测模型； COVACIU等[15]、蔡铭等[16]考虑车辆曲线行驶的特性，建立了环形交通口噪声预测模型。行人过街信号控制路口是城市常见的道路形态之一，然而国内对这种路口交通噪声预测模型的研究仍不多见。

本研究在考虑车辆加、减速状态下噪声排放的基础上，根据行人过街信号控制路口交通流的运行特性，利用能量叠加原理建立行人过街信号控制路口交通噪声预测模型，然后采用实验数据对模型进行验证，并在此基础上进一步探讨该类路口交通噪声的分布规律。

1 模型的建立

1.1 单辆车的噪声计算

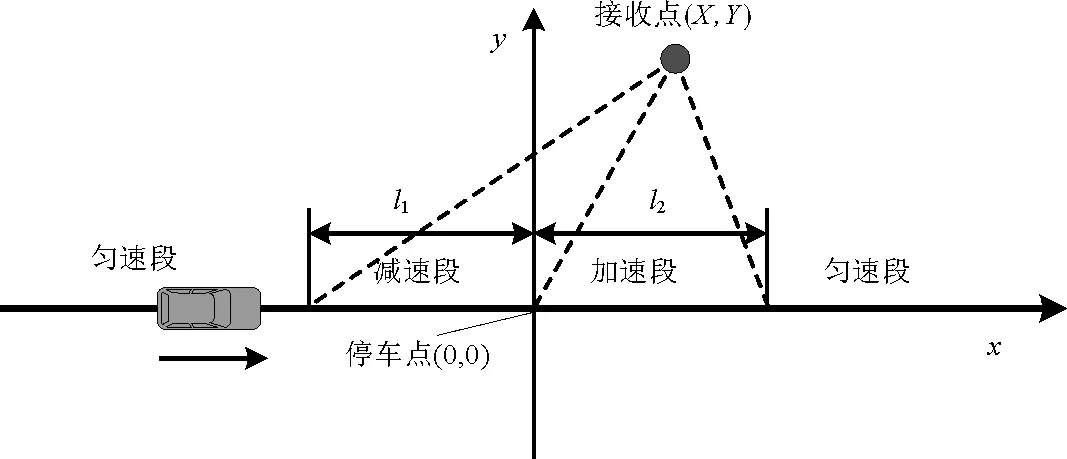
图1 车辆行驶阶段的坐标转化Fig.1 Coordinate transformation of vehicle traveling process

车辆通过信号控制路口的过程可简化为两种情况：若车辆到达路口时恰好为绿灯时间，则车辆按原来的速度匀速通过；若车辆到达路口时为红灯时间，则车辆必须经过匀速、减速、停车、加速、再匀速行驶的过程，对此过程进行坐标转化(见图1)，令停车点处的坐标为(0,0)，停车点上游减速段长度为l1m，停车点下游加速段长度为l2m，预测任一时刻接收点(X,Y)处的噪声。

车道上的单个车辆可看作半自由声场的点声源，忽略空气吸收和障碍物的影响，对于匀速通过的车辆，接收点(X,Y)处的噪声可表示为：

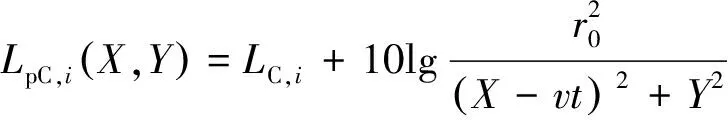
(1)

式中：LpC,i(X,Y)为接收点(X,Y)处的噪声，dB(A)；i为车型；LC,i为单辆车匀速行驶时在参照点的噪声，dB(A)；r0为车辆距参照点的距离，m，根据《公路建设项目环境影响评价规范》(JTG B03—2006)，r0取7.5 m；v为匀速通行的车速，m/s；t为车辆相对于停车点的行驶时间，s。

将道路近似看作无限长，则单辆车匀速通过时，接收点(X,Y)的等效声级为：

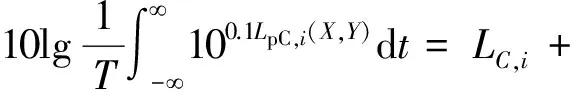
(2)

式中：Leq1,i(X,Y)为单辆车匀速通过时对接收点(X,Y)产生的等效声级，dB(A)；T为计算时间，s。

对于需停车的车辆，接收点(X,Y)的等效声级由以下几个过程组成：

(1) 匀速段等效声级：

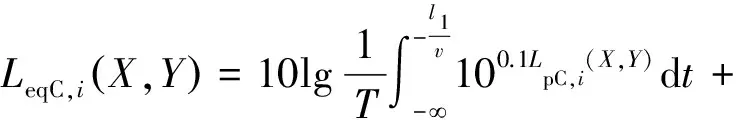
(3)

式中：LeqC,i(X,Y)为单辆车在匀速段行驶时对接收点(X,Y)产生的等效声级，dB(A)。

(2) 减速段等效声级：

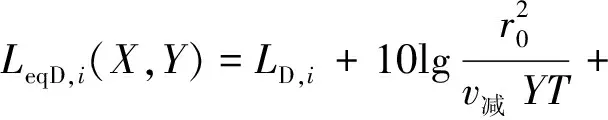
(4)

式中：LeqD,i(X,Y)为单辆车在减速段行驶时对接收点(X,Y)产生的等效声级，dB(A)；LD,i为车辆行驶时在参考距离r0处的噪声,dB(A);v减为减速段的平均车速，m/s。

(3) 停车怠速时的等效声级：

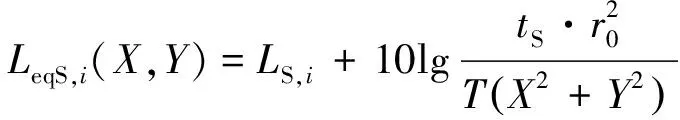
(5)

式中：LeqS,i(X,Y)为单辆车在停车怠速时对接收点(X,Y)产生的等效声级，dB(A)；LS,i为单辆车停车怠速时在参考距离r0处的噪声，dB(A)；tS为停车时间，s。

(4) 加速段等效声级：

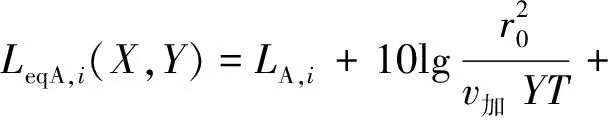
(6)

式中：LeqA,i(X,Y)为单辆车在加速段行驶时对接收点(X,Y)产生的等效声级，dB(A)；LA,i为单辆车加速行驶时在参考距离r0处的噪声，dB(A)；v加为加速段的平均车速，m/s。

因此，对于需停车的车辆，单辆车在整个行驶过程中，接收点(X,Y)的等效声级(Leq2,i(X,Y),dB(A))为：

Leq2,i(X,Y)=10lg(100.1LeqC,i(X,Y)+100.1LeqD,i(X,Y)+
100.1LeqS,i(X,Y)+100.1LeqA,i(X,Y))

(7)

1.2 单向单车道的噪声计算

在不出现二次排队的情况下，一个信号周期内需停车的车辆数为：

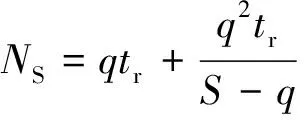
(8)

式中：NS为一个信号周期内需停车的车辆数，辆；q为车辆平均到达率，辆/s；tr为红灯时间，s；S为饱和流量，辆/s。

一个信号周期内可直接通行的车辆数为：

NC=q(tr+tg)-NS

(9)

式中：NC为一个信号周期内可直接通行的车辆数，辆；tg为绿灯时间，s。

在停车排队的车辆中，第j辆车的停车时间为：

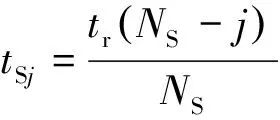
(10)

式中：tSj为停车车辆中第j辆车的停车时间，s。

设第i种车型的流量比例为pi，共有w种车型，则一个信号周期内，可直接通行车辆的等效声级为：

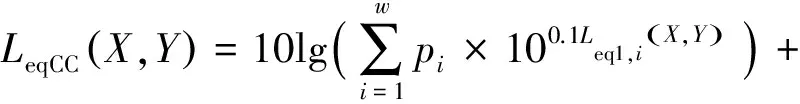
(11)

式中：LeqCC(X,Y)为一个信号周期内直接通行车辆对接收点(X,Y)处产生的等效声级，dB(A)。

对于停车排队的车辆，由于各车的停车位置和停车时间不同，假设停车排队时的车辆间距为dm，则第j辆车对接收点(X,Y)产生的等效声级可以用(X+j·d,Y)代替式(7)中的(X,Y)进行计算。其中，在单辆车停车怠速等效声级计算时，单辆车的停车时间根据式(10)计算。综上，停车排队的车辆在接收点(X,Y)产生的等效声级为：

(12)

式中：LeqSC(X,Y)为停车排队的车辆在接收点(X,Y)产生的等效声级，dB(A)。

单车道在一段时间内(通常为1 h)的等效声级为：

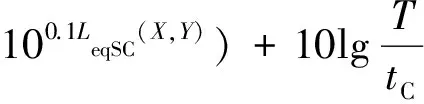
(13)

式中：LeqLane(X,Y)为单车道在一段时间内对接收点(X,Y)处产生的等效声级，dB(A)；tC为信号周期，s。

1.3 双向多车道的噪声计算

对于双向多车道的道路，以道路中心线为x轴，两停车线距离的中点为坐标原点建坐标系(见图2)，假设两停车线之间的距离为lm；道路中心线到第一车道的距离为d0m；车道宽度为dLm。由于坐标改变，可用(X+l/2,Y+d0+(n-1)dL)代替式(13)中的(X,Y)，得到正向第n车道的噪声。由于正向和反向车道具有中心对称性，因此可用坐标变换的方法计算反向车道的噪声。反向第n车道的噪声则可用(-X+l/2,-Y+d0+(n-1)dL)代替式(13)中的(X,Y)进行计算。因此，双向多车道对接收点(X,Y)产生的等效声级为：

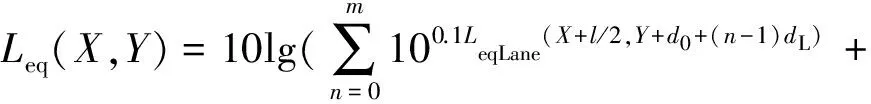
(14)

式中：Leq(X,Y)为双向多车道对接收点(X,Y)产生的等效声级，dB(A)；m为单向车道数。

2 模型验证

对广州市新港东路某行人过街信号控制路口的交通流量和交通噪声进行测量，测量时间为上午9：00—12：00。共布设11个监测点平行于道路分布，监测点间的距离为30 m，监测点高度均为1.2 m，如图2所示。该道路为双向8车道，车道宽度约3.5 m。交通流受两方向的交通信号控制，绿灯时间为50 s，红灯时间为40 s。交通噪声采用CENTER322型声级计进行测量，每隔1 s记录一次A计权声级。用测速计测得该道路的平均车速为61.2 km/h。交通量采用人工计数法进行统计，结果如表1所示。

图2 双向多车道坐标转化Fig.2 Coordinate transformation of multilane two-way streets

表1 交通量统计

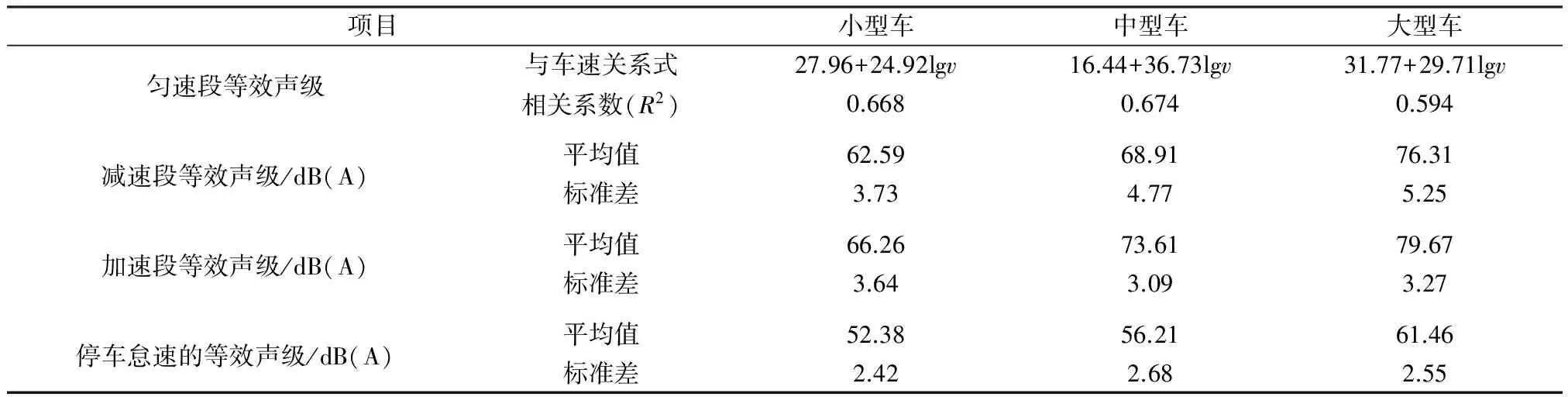
表2 车辆噪声排放测量结果

在前期工作中，对大型车、中型车、小型车3种车型的车辆在匀速、加速、减速和停车时排放的噪声进行了实验测量，结果如表2所示[17]。

为比较本模型(以下简称信号控制路口模型)与不考虑车辆加、减速影响的长直道路交通噪声预测模型[18](以下简称长直道路模型)的差别，用实测的车流量、车流速度、信号周期等参数分别代入2个模型进行计算。计算时间取1 h，饱和流量取1 800 辆/h，加速段和减速段的长度均设为80 m，单辆车的噪声排放按表2进行计算。

将两种模型预测的监测点等效声级计算结果与实测值进行对比，结果如图3所示。可以看出，由于车辆行驶速度的变化，路口附近噪声也有不同程度的起伏。不考虑车辆加、减速影响的长直道路模型不能反映路口附近的噪声变化，而本研究构建的信号控制路口模型预测与实测值吻合相对较好。信号控制路口模型对路口上游(负坐标段)停车线附近(-60～-30 m)噪声的预测值普遍低于实测值，原因可能由小部分车辆在停车线附近鸣笛引起。另外，部分车辆刹车时产生的噪声也将导致实测值偏高。此外，信号控制路口模型在路口上游段的预测效果较好，预测值与实测值较一致，而在路口下游段(正坐标段)，预测值比实测值高，最大误差约3 dB(A)。主要原因有两方面：一是路口下游段模型计算输入的车速与实际车速可能存在一定偏差，即实际车辆经过短距离的加速后车速未达到61.2 km/h；二是实测路口上游车辆排队经过路口时，交通量均匀分布在各车道，通过路口后部分车辆为获得较快速度而变道进入超车道，使路口下游靠近噪声传感器的右侧车道车流量较小，而信号控制路口模型未考虑车辆变道问题。

将信号控制路口模型与长直道路模型进行比较，并按图2所示的坐标系，根据两模型预测值的差值绘制等值线图，如图4所示。

由图4可见，与长直道路模型相比，信号控制路口模型的计算结果在减速段和加速段附近均有不同程度的降低，其中减速段附近噪声降低明显(约3 dB(A))，在两个方向的停车区域出现了关于坐标原点呈中心对称的“凹陷区”，而加速段附近噪声则下降较少。由此可知，利用长直道路模型预测行人过街信号控制路口的交通噪声是不适宜的。

3 结 语

根据能量叠加原理和交通流相关理论建立信号控制路口噪声预测模型，经与实测数据检验，该模型总体能正确反映路口附近车辆的加、减速给交通噪声带来的影响。与不考虑车辆加、减速影响的长直道路模型相比，信号控制路口模型的计算结果更接近实测值。根据信号控制路口模型预测结果，由于车辆速度下降的原因，行人过街信号控制路口减速段附近的噪声有约3 dB(A)的下降，在两个方向的停车区域出现了关于坐标原点呈中心对称的“凹陷区”，而加速段附近噪声则下降较少。

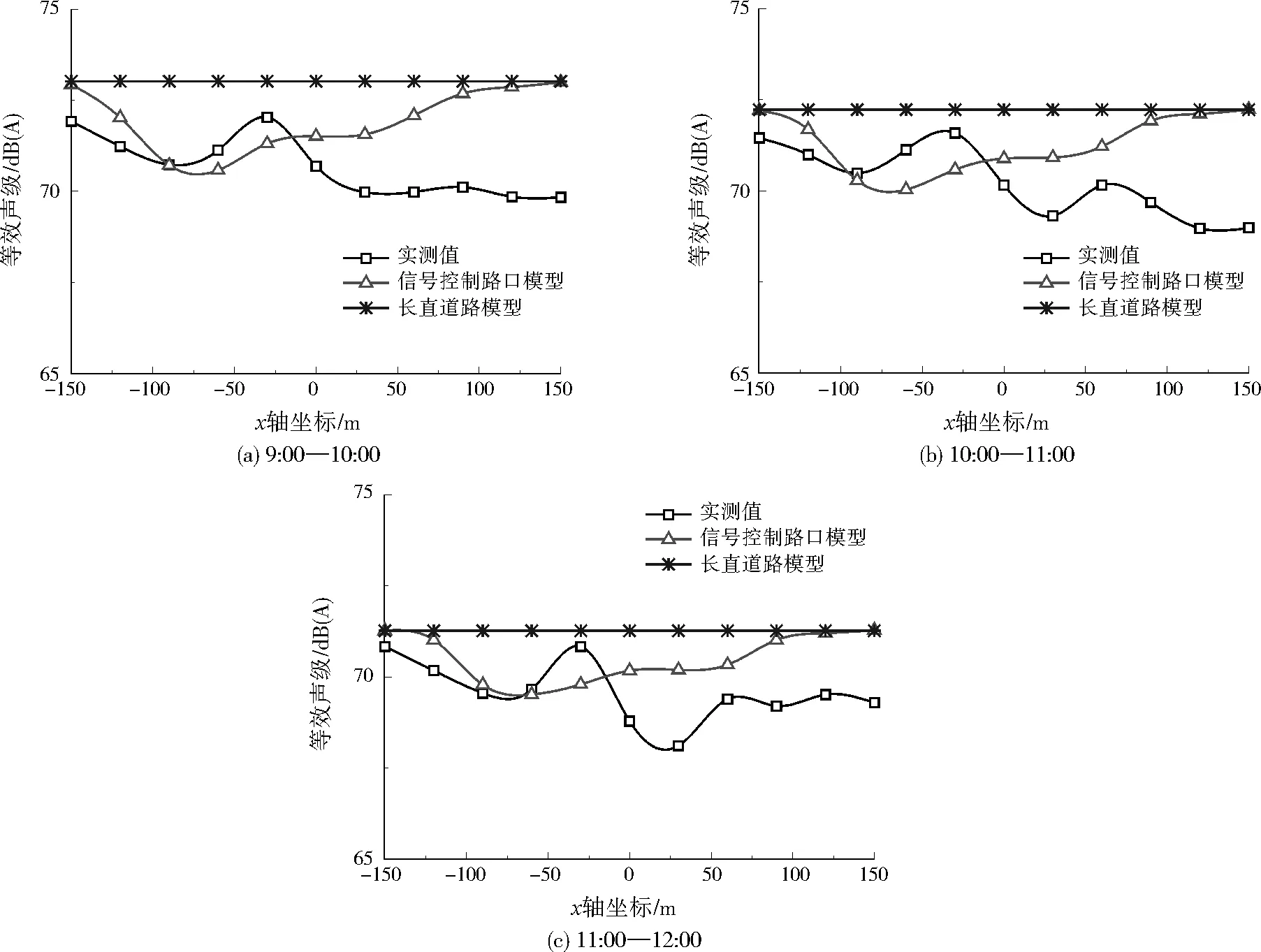
图3 预测值与实测值比较Fig.3 Comparison of predicted values and measured values

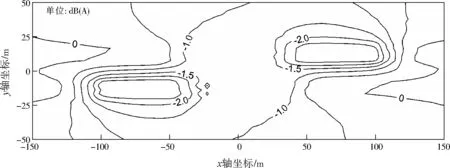
图4 差值分布Fig.4 Distribution of difference

[1] STEELE C.A critical review of some traffic noise prediction models[J].Applied Acoustics,2001,62(3):271-287.

[2] Federal Highway Administration.FHWA traffic noise model technical manual[EB/OL].[2015-07-20].http://www.fhwa.dot.gov/environment/noise/traffic_noise_model/old_versions/tnm_version_10/tech_manual/TNM10TechManual.pdf.

[3] TSUKUI K,OSHINO Y,BLOKLAND G V,et al.Study of the road traffic noise prediction method applicable to low-noise road surfaces[J].Acoustical Science & Technology,2010,31(1):102-112.

[4] CHO D S,MUN S.Development of a highway traffic noise prediction model that considers various road surface types[J].Applied Acoustics,2008,69(11):1120-1128.

[5] 张玉芬，钱炳华，戴明新．交通运输与环境保护[M].北京：人民交通出版社，2003．

[6] 林郁山，蔡铭，李锋．考虑加速度的交通噪声源强研究[J].应用声学，2012(4)：282-286．

[7] 蔡铭，谢林华，张磊．考虑行驶状态的水泥路机动车噪声排放模型[J].应用声学，2015(2)：175-182．

[8] MAKAREWICZ R,FUJIMOTO M,KOKOWSKI P.A model of interrupted road traffic noise[J].Applied Acoustics,1999,57(2):129-137.

[9] MAKAREWICZ R,KOKOWSKI P.Prediction of noise changes due to traffic speed control[J].The Journal of the Acoustical Society of America,2007,122(4):2074-2081.

[10] MAKAREWICZ R,KOKOWSKI P.Efficiency of noise reduction by a road speed bump[J].Archives of Acoustics，2007,32(3):631-642.

[11] 王波，王炜，刘浩．无控制交叉口交通噪声分析[J].东南大学学报(自然科学版)，2000，30(3)：96-99．

[12] 常玉林，王炜，王春燕．道路交叉口交通噪声预测模型研究[J].土木工程学报，2003，36(1)：75-79．

[13] 王超，蔡铭，丁建立．城市信号控制交叉口交通噪声预测模型研究[J].环境科学与技术，2015，38(6)：252-257．

[14] ABO QUDAIS S,ALHIARY A.Statistical models for traffic noise at signalized intersections[J].Building and Environment,2007,42(8):2939-2948.

[15] COVACIU D,FLOREA D,TIMAR J.Estimation of the noise level produced by road traffic in roundabouts[J].Applied Acoustics,2015,98:43-51.

[16] 蔡铭，王璐，李锋．考虑车流分布特性的环形交叉口交通噪声预测模型[J].环境科学与技术，2012，35(9)：163-166．

[17] 李锋．道路交通噪声传播衰减计算模型及动态模拟研究[D].广州：中山大学，2011．

[18] 张玉芬．道路交通环境工程[M].北京：人民交通出版社，2001．