双指数跳扩散模型下的交换期权定价
2016-03-12王宇帆
王宇帆
北京理工大学
双指数跳扩散模型下的交换期权定价
王宇帆
北京理工大学
本文研究了标的资产服从双指数跳扩散的交换期权定价。首先,介绍了双指数跳扩散模型与交换期权;其次,通过Girsanov定理对交换期权定价公式进行了测度变换;最后借助Hh函数的性质给出了双指数跳扩散模型下的交换期权定价公式。
交换期权;双指数跳扩散模型;Girsanov定理
1.引言
期权定价理论是现代金融数学的核心问题之一,1973年由Fischer Black和Myron Scholes[1]提出了著名的Black-Scholes期权定价模型,成为期权定价问题领域的基石,然而经典的Black-Scholes模型有两个主要缺陷:一是尖峰厚尾性质和非对称性质,即在经典B-S模型有着比正态分布更高的峰度和更厚的尾函数;二是“波动率微笑”,经典模型中隐含波动率是一个常数,而实际情况却是个类似于“微笑”形状的曲线。
交换期权是一种特殊的奇异期权,期权的持有者可以在到期日用一种标的资产换取另外一种标的资产。本文借鉴Kou文中研究欧式期权定价的方法,运用Girsanov定理和Hh函数的相关性质给出了双指数跳扩散模型下交换期权的数值解。
2.双指数跳扩散模型下的交换期权定价
2.1 双指数跳扩散模型
假设市场中有三个可连续交易的资产,一个无风险资产B和两个风险资产S1和S2,在风险中性测度Q下, ,假设风险资产S1和S2在t时刻的价值满足:
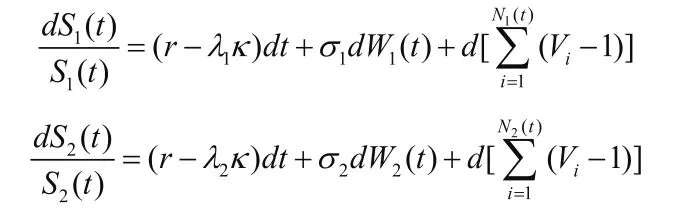
其中σ1和σ2分别表示两种风险资产在无跳跃发生时波动率,W1和W2为Q下的布朗运动满足 ,N1(t)和N2(t)分别是参数为λ1和λ2的泊松过程且相互独立,Vi是一系列非负的独立同分布随机变量,,令 有
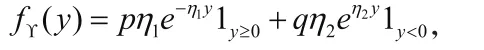
p>0表示资产价格向上跳跃的概率,q>0表示资产价格向下跳跃的概率,因此有p+q=1。假设所有的随机变量都是相互独立的。
用公式可以解得:
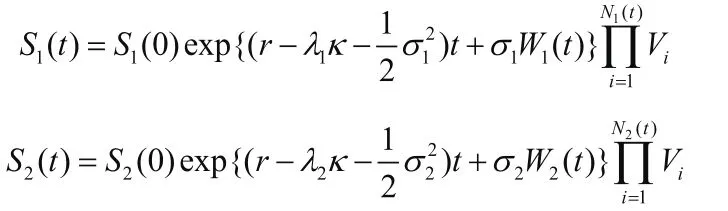
则由由此可知在初始时刻的期权价格应该满足:
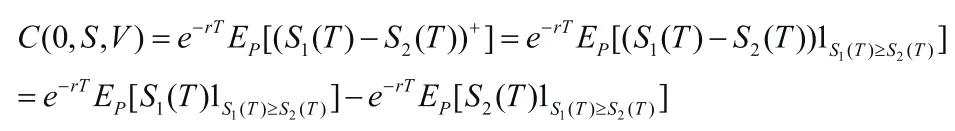
接下来分别计算前后两项。
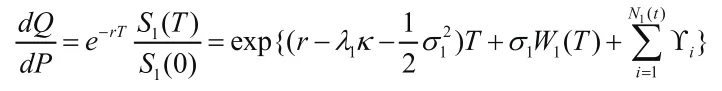
这样就有
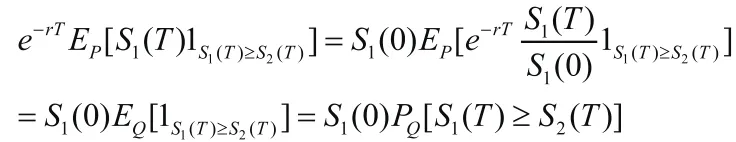
于是我们考虑Q测度下 的概率。
2.2 Hh函数与相关引理[7]
引理2.1对于任意的 ,有
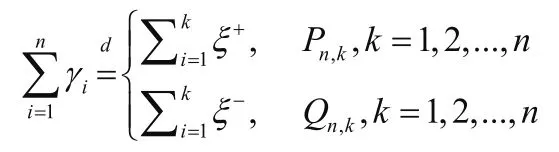
其中概率Pn,k与Qn,k分别为:
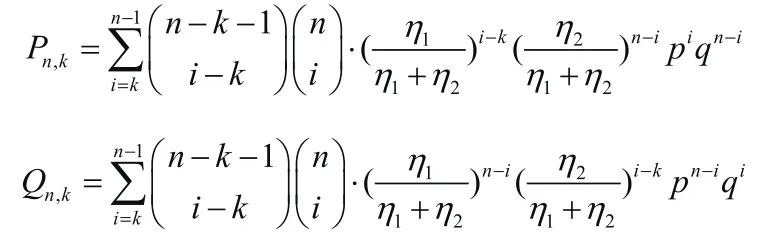
其中
这里ξ+与ξ-分别是参数为η1和η2的指数随机变量
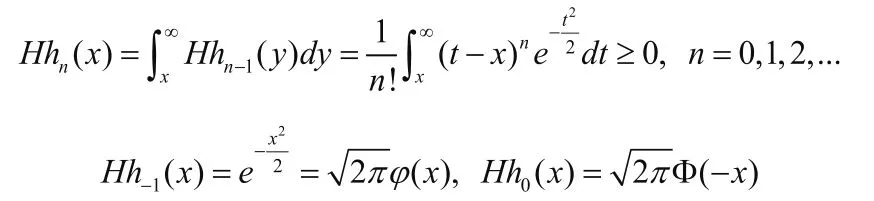
引理2.2
假设{ξ1,ξ2,…}是一列参数为η>0的独立同分布指数随机变量,Z是服从N(0,σ2)正态随机变量,则对于所有的有
(1)概率密度函数为(2)分布函数为
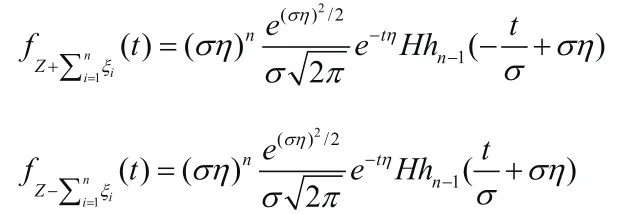
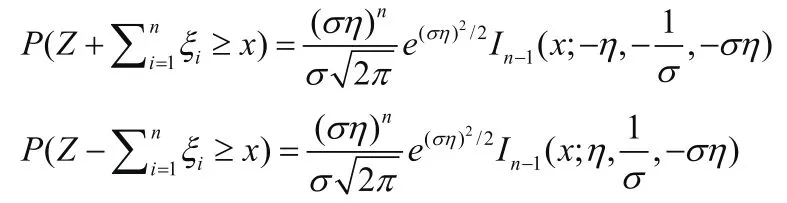
这两个引理将双指数随机变量转换为了两族单指数随机变量的和的概率
2.3 交换期权定价
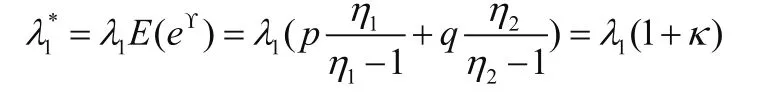
的泊松过程,N2(t)的跳频度不变,在Q下是独立
同分布的随机变量,概率密度函数为
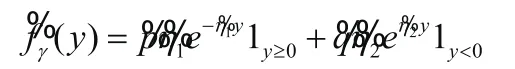
其中
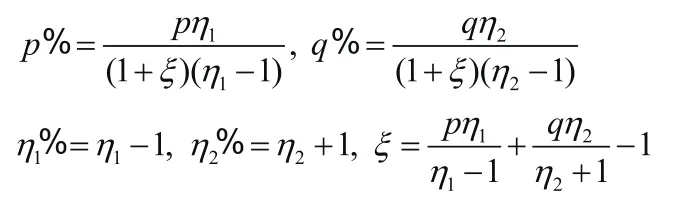
所以在Q测度下有
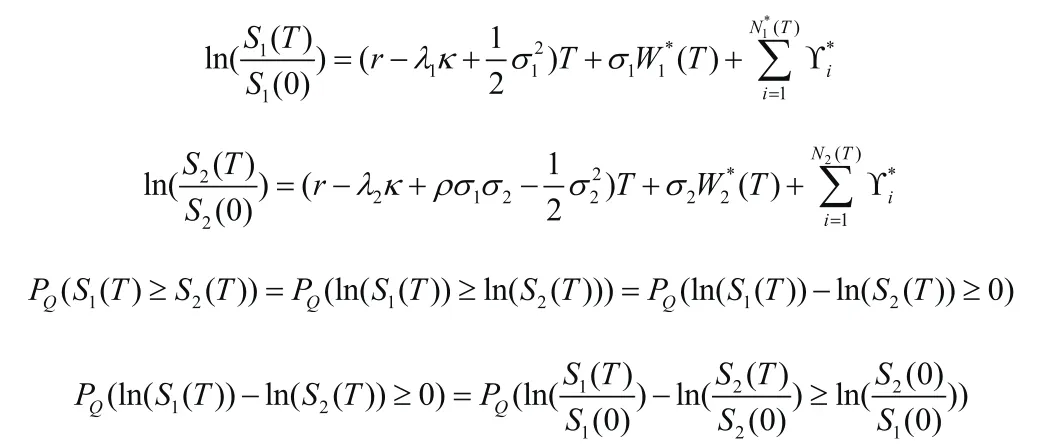
计算可得
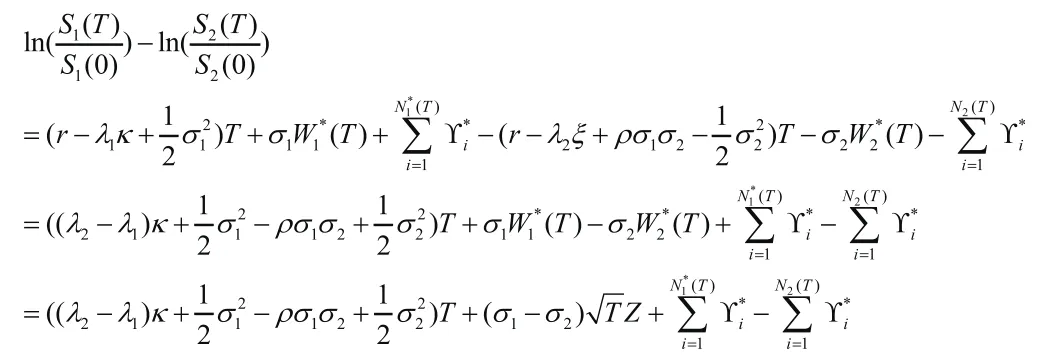
即有

其中
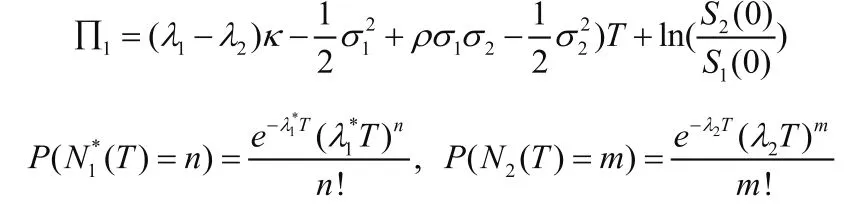
由引理2.1可得,
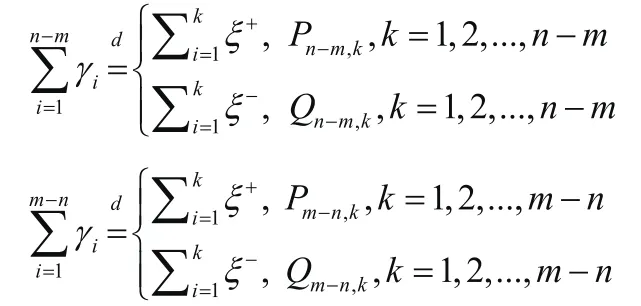
这里ξ+与ξ-分别是参数为η1和η2的指数随机变量。

所以可以计算得
综合上述可得到
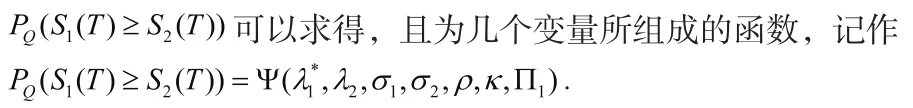
同理考虑
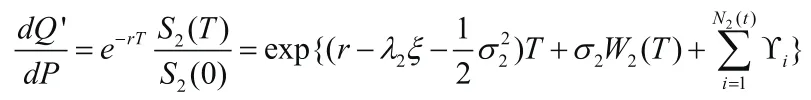
可得
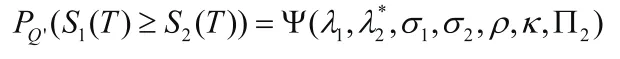
所以可以得到
定理3.1双指数跳扩散下的交换期权的定价为
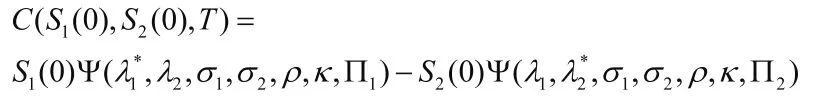
其中

3.结论
本文研究了双指数跳扩散下的交换期权定价,并运用Hh函数的相关性质与引理和Girsanov定理给出了显示解,本文中考虑的重点在于应用这些性质与引理解决交换期权定价,所以仅考虑风险资产的收益率和波动率为常数的情况。今后还可以进一步改进这个模型与数值解,例如考虑期望收益率和波动率依赖市场经济状态,其中经济状态可以用带切换的随机微分方程来表示。
[1]Black F, Scholes M. The Pricing of Options and Corporate Liabilities[J]. Journal of Political Economy, 1973, 81(3):637-54.
[2] Merton R C. Option pricing when underlying stock returns are discontinuous ☆[J]. Working Papers, 1975, 3(1–2):125-144.
[3]Hull J, White A. The Pricing of Options on Assets with Stochastic Volatilities[J]. Journal of Finance, 1987, 42(2):281-300.
[4]Barndorf-Nielsen O E. Processes of normal inverse type[J]. Finance & Stochastics, 1998.
[5]X. Guo. Information and option pricings[J]. Quantitative Finance, 2010,1(1):38-44.
[6]Kou S G. A jump diffusion model for option pricing with three properties: leptokurtic feature, volatility smile, and analytical tractability[C]// Computational Intelligence for Financial Engineering. IEEE, 2000:129 - 131.
[7]Kou S G. A Jump-Diffusion Model for Option Pricing[J]. Management Science, 2002, 48(8):1086-1101.
