自由度等于1的χ测验与u测验的数学关系
2016-03-11辛淑亮郭新梅
辛淑亮++++郭新梅
摘 要: 针对统计教科书上χ■测验与u测验关系模糊不清的情况,本文用3个事例进行了χ■测验、矫正的χ■■测验、u测验、矫正的u■测验.结果表明,对于k=2和2×2的次数资料,自由度df=1时,可以用χ■测验;也可以用u测验.数学关系为:χ■=u■;χ■■=u■■;χ■■=χ■■;χ■■=u■■.
关键词: 假设测验 自由度 χ■测验 u测验
在科研实践中,许多试验结果用百分率表示,如杀虫率、发芽率、坐果率、合格率等.这些百分率系由统计某一属性的个体数目求得,属间断性的计数资料.这类数据假设测验的方法主要分两类:百分率数据用u测验;计数资料用χ■测验.很多统计学书介绍了相关的假设测验方法[1-5],但是都没有说明两种假设测验的关系.同时,我们在使用相关教材时发现书中出现了一些有待商榷的例题.针对这些问题,我们利用相关教材中的例题,对两种假设测验的关系进行了数学推导,以明确χ■测验与u测验的数学关系.
1.单个百分率测验与适合性χ■测验的关系
例1:用基因型纯合的糯玉米和非糯玉米杂交,按遗传学原理,预期F■植株上糯性花粉粒的P■=0.5,现在一视野中检视20粒花粉,得糯性花粉8粒,问此结果和理论百分率P■=0.5是否相符[1]?
解法1:k=2组次数资料的适合性χ■测验
假设H■:总体分布符合1∶1,对HA:总体分布不符合1∶1.
显著水平α=0.05
测验计算:
理论次数E■=20×0.5=10
E■=20×0.5=10
χ■=(8-10)■/10+(12-10)■/10=0.8
df=2-1=1
x■■=3.84
统计推断:实得χ■<χ■■,故概率P>0.05.接受H■:总体分布符合1∶1的理论分布,差异不显著.
解法2:k=2组次数资料的适合性χ■■测验
χ■分布是连续性的,而次数资料则是间断性的.由间断性资料算得的χ■值有偏大的趋势,尤其是自由度df=1时,用连续性分布作χ■测验时,容易发生第一类错误.故在假设测验时,进行连续性矫正,采用矫正的χ■■测验.
解:假设H■:总体分布符合1∶1,H■:总体分布不符合1∶1.
显著水平α=0.05
测验计算:
χ■■=(|8-10|-0.5)■/10+(|12-10|-0.5)■/10=0.45
df=2-1=1
χ■■=3.84
统计推断:实得χ■■<χ■■,故概率P>0.05.接受H■:总体分布符合1∶1的理论分布,差异不显著.
解法3:单个百分率的u测验
在理论上,这类百分数应按二项分布进行假设测验.但是,如果样本容量n较大,p不过小,np和nq皆大于5时,二项分布趋近正态分布.因而,可以将百分数资料做正态分布处理,作近似u的测验.
解:假设H■∶P=0.5,H■∶P≠0.5.
显著水平α=0.05
测验计算:
■=8/20=0.4
■ ■=■=0.111803
u=(0.4-0.5)/0.111803=-0.89443
u■=1.96
统计推断:实得|u|
解法4:单个百分率的u■测验
因为二项分布的百分率系由计数某一属性的个体数目计算得来,属于间断性的二项分布.用连续性的正态分布作u测验时,容易发生第一类错误.所以在假设测验时,进行连续性矫正,采用矫正的u■测验.
解:假设H■∶P=0.5对H■∶P≠0.5
显著水平α=0.05
测验计算:
u■=(|0.4-0.5|-0.5/20)/0.111803=0.67082
u■=1.96
统计推断:实得u■
综上所述,适合性χ■测验与单个百分率u测验的关系:
对于二项分布即k=2的次数资料,自由度df=2-1=1,适合性χ■测验与单个百分率测验有如下数学关系:
u■=(-0.89443)■=0.8=χ■
u■■=0.67082■=0.45=χ■■
u■■=1.96■=3.84=χ■■
u■■=2.576■=6.64=χ■■
u■■=χ■■
由此可见,当自由度df=1时,两尾u测验与一尾χ■测验相对应.
图1 k=2组次数资料和2×2表次数资料的统计方法
2.两个百分率测验与独立性χ■测验的关系
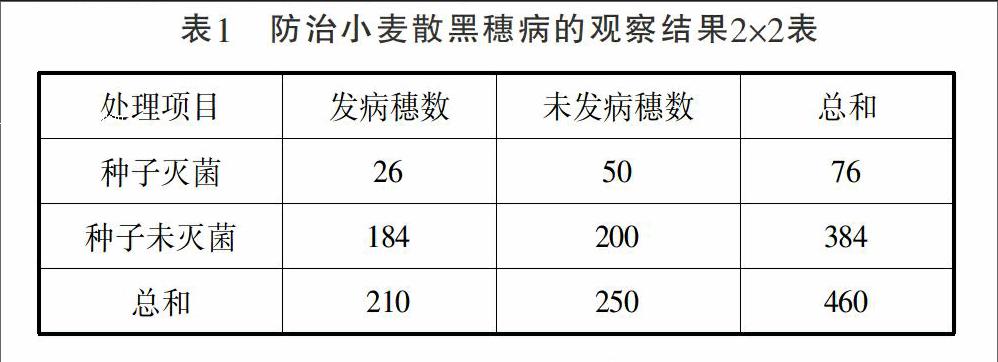
例2:调查经过种子灭菌处理与未经种子灭菌处理的小麦发生散黑穗病的穗数,得相依表1,试分析种子灭菌与否和发生散黑穗病多少是否有关[1]?
表1 防治小麦散黑穗病的观察结果2×2表
解法1:2×2表次数资料的独立性χ■测验
解:假设H■:独立,H■:不独立.
显著水平α=0.05
测验计算:
理论次数E■=76×210/460=34.69565
E■=76×250/460=41.30435
E■=384×210/460=175.3043
E■=384×250/460=208.6957
χ■=(26-34.69565)■/34.69565+(50-41.30435)■/41.30435
+(184-175.3043)■/175.3043+(200-208.6957)■/208.6957
=4.803676
df=(2-1)(2-1)=1
χ■■=3.84
统计推断:实得χ■>χ■■,故概率P<0.05.否定H■接受H■:不独立,差异显著.
解法2:2×2表次数资料的独立性χ■■测验
解:假设H■:独立,H■:不独立.
显著水平α=0.05
测验计算:
χ■■=(|26-34.69565|-0.5)■/34.69565+(|50-41.30435|-0.5)■/41.30435+(|184-175.3043|-0.5)■/175.3043+(|200-208.6957|-0.5)■/208.6957=4.267135
df=(2-1)(2-1)=1
χ■■=3.84
统计推断:实得χ■■>χ■■,故概率P<0.05.否定H■接受H■:不独立,差异显著.
解法3:两个百分率u的测验
解:假设H■:P■=P■,H■:P■≠P■.
显著水平α=0.05
测验计算:
■■=26/76=0.342105
■■=184/384=0.479167
■=(26+184)/(76+384)=0.456522
■=1-0.456522=0.543478
S■=■=0.062536
u=(0.342105-0.479167)/0.062536=-2.19173
u■■=1.96
统计推断:实得|u|>u■■,故概率P<0.05.否定H■接受H■,两者差异显著.
解法4:两个百分率的u■测验
解:假设H■:P■=P■,对H■:P■≠P■.
显著水平α=0.05
测验计算:
u■=(|0.342105-0.479167|-0.5/76-0.5/384)/0.062536=2.065705
u■=1.96
统计推断:实得u■>u■,故概率P<0.05.否定H■接受H■:P■≠P■,差异显著.
综上所述,独立性χ■测验与两个百分率u测验的关系:
对于2×2表的次数资料,自由度df=(2-1)(2-1)=1,独立性χ■测验与两个百分率u测验有如下数学关系:
u■=(-2.19173)■=4.803676=χ■
u■■=2.065705■=4.267135=χ■■
u■■=1.96■=3.84=χ■■
u■■=2.576■=6.64=χ■■
由此可见,当自由度df=1时,两尾u测验与一尾χ■测验相对应.u测验的两尾临界值与χ■测验的一尾临界值相等,即u■■=χ■■.
3.讨论
对于例1,在教材中是这样进行假设测验的■.
解:假设H■∶P=0.5,HA∶P≠0.5.
显著水平α=0.05
测验计算:
np=20×0.5=10
S■=■=2.19089
t■=(|8-10|-0.5)/2.19089=0.684653
df=20-1=19
t■=2.093
统计推断:实得t■
因为根据无效假设,可以计得■ ■.而且已知σ时,无论样本大小,都可以用u测验.所以,上述计算中选用t测验不合适,t■■=0.684653■=0.46875≠χ■■.这里应用S■的计算公式不妥当.下面用事例间接证明.
例3:某食品厂的一条生产线上的产品组成指标为:一级品∶二级品=7∶3.现随机抽取了20个产品做检验,得一级品13个,二级品7个.问其产品组成比例是否达到一级品占70%的生产指标[2]?
对于例3,在教材中是这样进行假设测验的[2].
解:假设H■:P≥0.7,H■:P<0.7.
显著水平α=0.05
测验计算:
■=13/20=0.65
■ ■=■=0.10247
u■=(|0.65-0.7|-0.5/20)/0.10247=0.243975
u■=1.645
统计推断:实得u■
可以证明,u■■=1.645■=2.706=χ■■,说明u测验的一尾临界值u■■与χ■测验的一尾临界值χ■■相等,即u■■=χ■■.
4.结论
(1)对于k=2组次数资料,可以用适合性χ■测验;也可以用单个百分率的u测验.
(2)对于2×2表的次数资料,可以用独立性χ■测验;也可以用两个百分率的u测验.
(3)百分率u测验与χ■测验的数学关系为:u■=χ■.
(4)百分率矫正的u■测验与矫正的χ■■测验的数学关系为:u■■=χ■■.
(5)测验的两尾临界值与χ■测验的一尾临界值间,有如下数学关系:u■■=χ■■.
(6)测验的一尾临界值与χ■测验的一尾临界值间,有如下数学关系:u■■=χ■■.
参考文献:
[1]盖钧镒.试验统计方法[M].北京:中国农业出版社,2000:91,135.
[2]王钦德,扬坚.食品试验统计与统计分析[M].北京:中国农业大学出版社,2010:62.
[3]辛淑亮.现代农业试验统计[M].北京:中国统计出版社,1999.
[4]莫惠栋.农业试验统计[M].上海:上海科学技术出版社,1984.
[5]刘权.果树试验统计及统计[M].北京:中国农业出版社,1997.
基金项目:山东省应用型人才培养特色名校建设工程.
