“愤悱术”和“产婆术”启发式教学实践显著性检验研究

陈一飞

摘要：文章通过受试的两个班级对教学方法进行研究，甲班是采用“愤悱术”和“产婆术”的启发式教学方法，乙班按原来的传统的教学方法。然后根据两班的期末成绩进行统计学意义上的科学分析，特别是应用显著性检验手段得出结论，即新的教学实践明显优于传统的教学方法。

关键词：“愤悱术”;“产婆术”;启发式教学;显著性检验;研究

一、前言

教师在课堂教学中要打破传统束缚学生思维发展的旧模式，遵循以人为本的观念，给学生思维提供最大的空间，项目根据“应用有机化学”教学大纲，把培养学生的创新素养作为教学的重点。转变学生的学习方式，既要让他们“学会”，也要“会学”，因此我们在“应用有机化学”课堂教学中，基于“愤悱术”和“产婆术”启发式教学的课堂教学策略的基本理论依据，设计了“应用有机化学”课堂教学改革的几种模式：主动性模式、主体性模式、情感性模式、可持续性模式、举一反三学习模式[1][2]。

“应用有机化学”“愤悱术”和“产婆术”的启发式教学策略源于一般启发式教学策略，是一般启发式教学策略的应用，具有一般启发式教学策略的特点。通过对甲班进行试验，而乙班的教学方法保持原状。根据期末考试成绩，进行显著性检验分析[3][4]。

二、以分析性统计检验误差，以确认从样本推断总体的可靠性

（一）u检验和t检验理论依据

统计检验是准确解释研究结果的前提，其方法可分为参数统计检验和非参数统计检验两类。在中小学教育科研中，通常以参数统计检验为主，其中u检验和t检验是两种最常用的检验方法。[5]

在教育统计中常以正态曲线分布下面积的95%或99%的理论u值为差异显著性的临界值，取0.05和0.01位两个显著水平。若样本的u值等于或大于95%或99%的理论u值（分别为1.96和2.58），即表明样本的平均数不超过 μ±1.96σ或 μ±2.58σ的区间。也就是说，样本来自同一总体的可能性（即概率P小于0.05或0.01）。在统计上将P≤0.05的差异称为显著差异，将P≤0.01的差异称为非常显著差异。反之，若样本的u值小于95%的理论z值，则表明样本来自同一总体的概率P>0.05，统计上称为差异不显著。

由于u检验要求样组的规模较大（n>30，严格地说，应以n>50为大样本），因此，对于小样本的检验通常都采用比较两个平均数以确定它们之间的差值是真的差值而不是偶然差数的t检验。在同一概率下，自由度越大，t值就越小;在自由度相同的情况下，则概率越小，t值越大。

（二）本次受试样本采用t检验

t检验方法检验样本之间有无真正的差异（由操纵自变量引起的差异，而不是由抽样误差等引起的差异），其基本程序为：①对试验样本所在的总体提出假设;②确定显著水平;③在无效假设成立的前提下，研究统计量的抽样分布，计算出检验统计量;④估计相对概率P，根据小概率原理作出统计推断。

1.建立虚无假设

差异检验是以“反正”为特点的逻辑推理过程。其基本思想是，为了证实各样本均数有显著差异，可首先假设被比较的样本均数（或百分数）没有显著差异，即假定它们是来自同一总体的，它们之间的差数为0，即便有差异，也纯粹属于随机误差，这种假设，在统计上称为“虚无假设”或“无效假设”（通常以H0表示）。倘若虚无假设成立的概率（通常以P表示）很小（P≤0.05，或P ≤0.01），则根据小概率原理“概率很小的时间在一次实验中是几乎不可能发生的”，就可拒绝虚无假设，即原来假定的各样本来自同一总体的可能性是极小的，从而可确定被比较的各数值之间的差异确实反映了自变量的处理效应。反之，如果P值比较大（P>0.05），我们就将接受虚无假设，认为被比较的各数值之间的差异完全是由随机误差造成的。

2.计算t值

计算t值首先需要考虑所检验的样本是相互独立的、互不关联的，还是相互关联的，并依据此选择相应的计算公式。这就是所谓的“独立样本”，是指两个样本的抽取互不影响，即受试者随机地被分配于两个样本之中，它们之间没有成对的关系。关于“相关样本”主要有两种情况：一种是对同一种研究对象进行两次检测所得到的两组数据;另一种是对两个并非通过随机抽样组成的配对组进行同种检测所得到的两组结果。如果两个配对组是通过随机抽样而构造的等值组，则由同种检测所得到的两组数据只能属于独立样本，而不能视作相关样本。

3.进行统计决策实例

即通过以t值与理论t值的比较，做出拒绝或接受虚无假设H0的决策。

如果采用的是t检验，则其决策程序为：

（1）根据自由度df，从t值表中查出0.05显著性水平上的临界值t（df）0.05和早0.01显著性水平上的临界值t（df）0.01。

例如，对n=40的样组进行t检验，则其自由度df=40-1=39。据此，可从上表中分别查得：

t在0.05显著性水平上的临界值：t（39）0.05 = 2.020;

t在0.01显著性水平上的临界值：t（39）0.01 = 2.703。

（2）将计算所得的t值与查表所得的临界值作比较，并根据下表进行统计决策。现在，让我们通过实例来进一步对统计检验问题作出具体的说明。试分析新的教学方法在提高学生数学水平方面与原来的教学方法有无显著差异。具体两个班级期末考试成绩数据见表1、表2。

由于n =40，为小样本，可采用t检验。检验步骤如下：

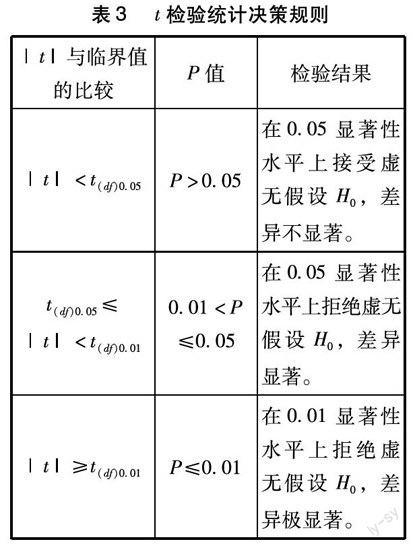
（3）计算t值。由于乙班为没有进行试验的考试结果，所以以乙班为基准进行计算，计算结果为：t=（78.90-70.08）/1.49 =5.92。t检验统计决策规则见表3。

≤0.05在0.05显著性水平上拒绝虚无假设H0，差异显著。|t|≥t（df）0.01 P≤0.01 在0.01显著性水平上拒绝虚无假设H0，差异极显著。

（4）统计决策。将实际所得的t值与理论t值相比较。比较结果为：

t=5.92≥t（df）0.01=3.499，即P≤0.01。在0.01显著性水平上拒绝虚无假设H0，表明差异极显著。

三、结语

在0.01显著性水平上拒绝虚无假设H0，表示采用“愤悱术”和“产婆术”启发式教学方法的学生在期末考试成绩方面有非常显著的差异，且甲班学生的成绩明显优于乙班学生。

采用“愤悱术”和“产婆术”启发式教学方法安排教学内容的教法与原来的教法相比，其教学效果在一般情况下是有极其显著差异意义的，即这种教学方法优于原来的教学方法，因而是可行的。

参考文献：

[1]靳乃铮.启发式教学[M].北京：北京师范大学出版社，2002.

[2]卢小男.信息技术环境下再论数学启发式教学[D].大连：辽宁师范大学，2010.

[3]焦家俊，任玉杰，钱旭红.有机化学探索式教学实践[J].化工高等教育，2007，24（4）：82—84.

[4]孟志芬.提高学生兴趣的有机化学教学法[J].大学化学，2006，21（1）：20—23.

[5]杨章宏.教育科研过程[M].乌鲁木齐：新疆大学出版社，2000.