解答概率问题中的几个关键点

解答概率问题中的几个关键点

◇山东油文玉

概率是高中数学主干内容之一,能有效考查考生分析、解决实际应用问题能力.概率与现实生活联系密切,是新课标考查应用性理念的一个很好的落脚点,因此备受高考命题人的关注．下面笔者以2015年湖南卷中的概率题为例,赏析命题特色,并对常考题型的解法进行总结,供同学们参考.

题目(2015年湖南卷)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.

(1) 求顾客抽奖1次能获奖的概率;

(2) 若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望．

1准确识别事件类型

处理本题首先要分清从甲箱中摸一球是红球与从乙箱中摸一球是红球这2个事件是相互独立事件.从甲箱中摸一球是红球从乙箱中摸一球非红球和从甲箱中摸一球非红球从乙箱中摸一球为非红球这2个和事件彼此互斥．

(1)记事件A1={从甲箱中摸出的1个球是红球},A2={从乙箱中摸出的1个球是红球}；

B1={顾客抽奖1次获一等奖},B2={顾客抽奖1次获二等奖},C={顾客抽奖1次能获奖}.

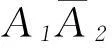
2正确计算相应事件发生的概率

探求一个事件发生的概率关键要分清事件的性质,若为等可能事件的概率常用排列组合等相关知识解决,若为互斥或者对立事件的概率则需要运用与之相关的和、差事件等知识解决.

P(A1)(1-P(A2))+(1-P(A1))·P(A2)=

故所求概率为

3不重不漏列出离散型随机变量概率分布列

对于独立重复试验是在同样的条件下重复地、各次之间相互独立地进行的一种试验.判断是否为独立重复试验的关键是每次试验事件A的概率不变,并且每次试验的结果同其他各次试验的结果无关,重复是指试验并非一次,而是多次,但要注意重复事件发生的概率相互之间没有影响.

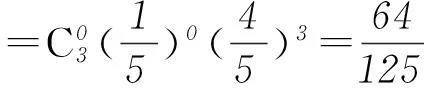
故X的分布列为

X0123P64/12548/12512/1251/125

X的数学期望为E(X)=3×1/5=3/5.

总之,概率是高中数学新增的教学内容,是新课程高考的亮点和热点,是中学数学知识的一个重要交会点,这类试题题型新颖灵活,综合性强,充分显示了新课标中所倡导的“新教材、新高考要体现时代气息”,为此,在复习备考中注重知识的积累与运用,以数学基础知识为依托,培养解题的思维过程及思维能力,进而顺利地解决新颖的问题.

(作者单位：山东日照莒县二中)